电磁惯性质量阻尼器对斜拉索的减振性能分析

谢 静， 袁 波， 郑 勇

(贵州大学空间结构研究中心，贵州省结构工程重点实验室，贵阳 550000)

随着公路工程技术的发展，集跨越能力与美学特性于一体的斜拉桥越来越多的运用于实际工程中。斜拉索做为斜拉桥的主要构件，在风雨激振、桥面荷载振动等激励下，会产生较大的振荡，影响桥梁的行车安全，造成拉索结构疲劳损伤，进而影响桥梁使用寿命。在确保控制效果和保留斜拉桥美观性的前提下，一般采用机械阻尼减振措施，通过在桥索上安置阻尼器的方式进行振动控制。将惯性质量运用在减振装置中的思想最早来源于1909年，Dan Hartog[1]最早提出利用惯性质量的动力吸振概念，经过多年来的研究与改进[2-6]质量型阻尼器如调谐质量阻尼器(tuned mass damper,TMD)、惯性质量阻尼器(inertial mass damper，IMD)得到了广泛的应用。黏滞型阻尼器如磁流变(magneto rheological，MR)阻尼器因其具有自重轻，减振性能优越等特点，近年来越来越多的应用于实际工程中。为了解决MR阻尼器外部供能问题，陈政清等[7-9]提出利用发电机、滚珠丝杠等组成的MR阻尼器自供电的复合减振系统。基于质量型阻尼器的吸振耗能特点，利用惯性质量进行能量收集的方法[10-14]也得了大量的研究。电磁惯性质量阻尼器(electromagnetic inertial mass damper，EIMD)是一种减振性能优越的半主动无源式阻尼器，通过滚珠丝杠的位移增效机制，将惯性质量单元与电磁阻尼器并联组成一种新型的高效阻尼器，电磁阻尼由内置直流发电机提供，能在保证减振效果的前提下将吸振器得到的一部分振动能转化为电能，在桥索振动控制方面有很好的应用。

Nakamura等[15]提出了EIMD的力学模型，通过公式理论推导得出了EIMD的阻尼力调节原理，并用实验验证了模型的正确性。Zhu等[16]在Nakamuray的基础上深入研究，提出为了与实验数据拟合更好，使计算结果更加精确，需要考虑EIMD力学模型中的寄生阻尼项，即阻尼器运行过程中的各种摩擦损耗；同时，他验证了EIMD内置直流发电机进行能源收集与利用的可靠性，提出能量收集模型。汪志昊等[17]进行了斜拉索EIMD减振试验，在验证EIMD安置在斜拉索上的减振效果同时，测试了EIMD惯性质量和阻尼参数对平面内振动的影响，证明EIMD具有良好的减振效果，并且通过试验得出阻尼器的惯性质量负刚度不会在实际工程中造成斜拉索减振系统不稳定。将EIMD固定在桥面上，与拉索形成耦合结构，通过惯性质量和电磁阻尼降低斜拉索的振动位移。

当前国内对于斜拉索-EIMD耦合振动系统的理论研究较少，本文基于D’Alembert原理建立斜拉索-EIMD非线性自由振动动力方程，进行数值模拟，验证阻尼器对拉索平面内外振动的减振性能。建立斜拉索-EIMD线性自由振动方程，分析拉索垂度对阻尼器减振效果的影响。

1 阻尼器模型

1.1 阻尼器力学模型

电磁惯性质量阻尼器(EIMD)是一种由直流发电机、惯性飞轮、滚珠丝杠、齿轮箱、传力杆组成的一种无源阻尼器，如图1所示。EIMD通过旋转飞轮产生较大的惯性质量，并通过内置直流发电机产生可变阻尼。较大的惯性质量可以减少作用在结构表面的振动激励，延长结构自然周期，可变阻尼增加了结构的阻尼系数，也起到了补偿普通质量调谐阻尼器(IMD)由于惯性质量大而导致的阻尼系数降低；同时直流发电机可将部分结构振动能转化为可供收集利用的电能。

(a) 缩小比例的EIMD

将球状螺母、飞轮和直流发电机用滚珠螺杆和直线运动导轨连接起来，从而实现将线性运动转换为旋转运动的过程；连接齿轮箱可以显著增加飞轮和直流发电机的转速，进一步提高了惯性和电磁阻尼。

EIMD非线性力学模型可表示为

(1a)

(1b)

(1c)

式中：Fd为EIMD阻尼力；me为阻尼器的等效惯性质量；y为杆端位移；cem为电磁阻尼系数；cm为寄生阻尼黏滞系数；fc为库伦摩擦力；sgn表示符号函数；λ为滚珠丝杠换能效率；ng为齿轮箱转动比率；l为滚珠丝杠尺寸参数；If为飞轮惯性矩；Im为直流发电机惯性矩；Kem为直流发电机机器常数；Rcoil为直流发电机的线圈电阻；Rload表示ELMD的负载电阻。

式(1a)表明EIMD总阻尼力由惯性质量、电磁效应产生的阻尼力和寄生阻尼力组成，寄生阻尼力对应阻尼器的各种机械损耗，包括：滚珠丝杠和滚珠轴承及直流发电机和齿轮箱的摩擦损耗、直流发电机的风阻损耗和磁损耗等。EIMD的非线性模型如图2所示。

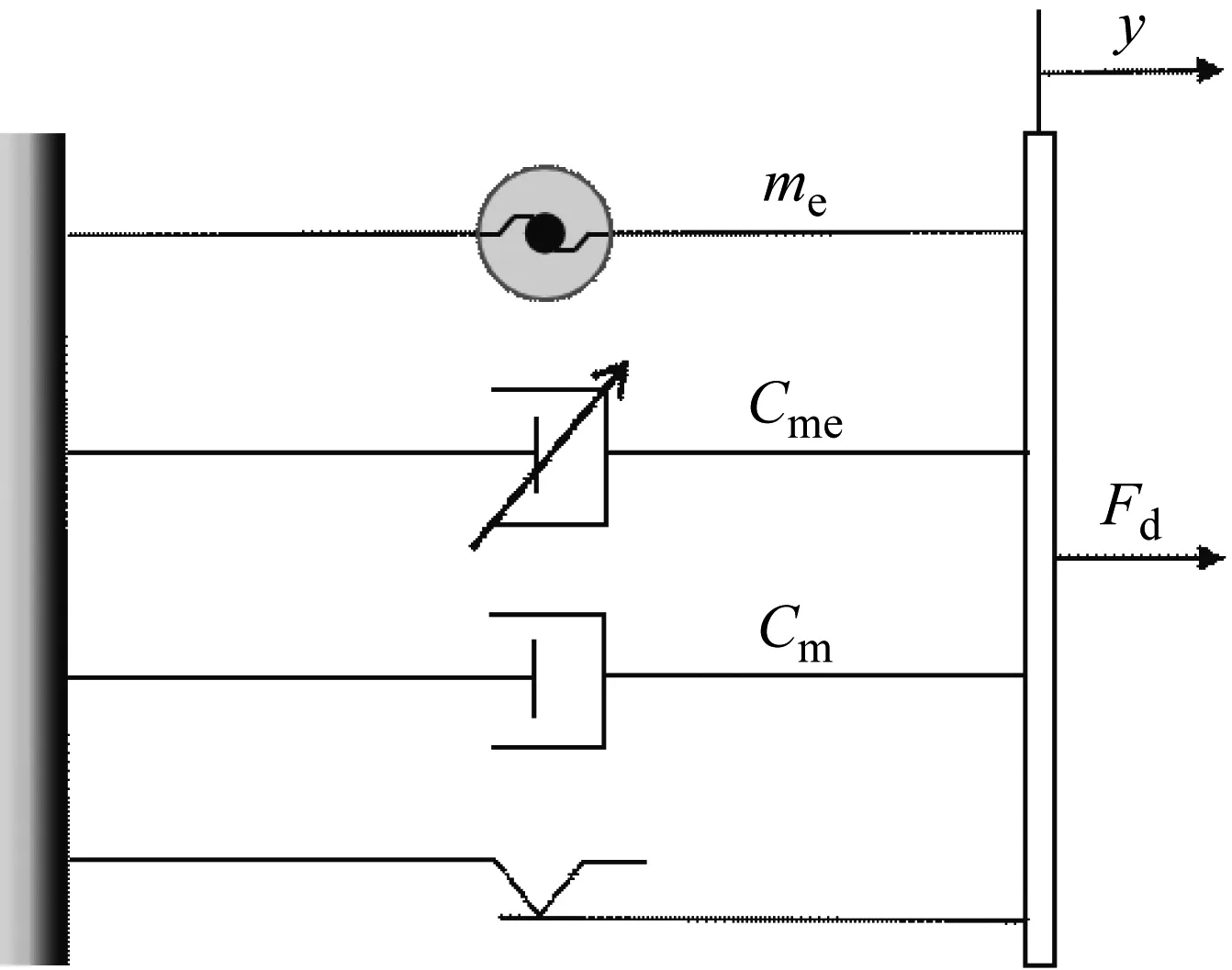
图2 EIMD的非线性模型

式(1b)表式EIMD可以通过放大If、Im来产生较大的惯性质量。同时，式(1c)表明EIMD可以通过改变负载电阻Rload来调节阻尼力，当Rload为0时系统相当于短路状态，电磁阻尼达到最大值，当Rload无限大时系统相当于开路状态，电磁阻尼接近于0。

1.2 ELMD电能收集模型

1.2.1 能量流动过程

EIMD吸收的能量由飞轮动能和阻尼能量组成。总阻尼能是由寄生阻尼能与电磁阻尼能叠加组成，其中前者转化为热能耗散，后者由直流发电机转换为电能。一部分电能被直流电机线圈耗散，另一部分电能传到外部收集利用；然而，外部收集电能的电路(EHC)本身也将消耗部分电能，如图3所示。

图3 EIMD的能量流动

根据能量平衡原理，假设输入振动为平稳振动，飞轮动能变化率(ROC)为0，功率流由式(2)表示

pin=pp+pem=pp+pcoil+pg=

pp+pcoil+pehc+pout

(2)

1.2.2 功率预测

当输入的振动激励是一个振幅不变的谐波激励时，Zhu等认为输出功率pout与振动频率相关，输出功率随振动频率的增加而增加。当采用阻抗匹配策略(即Rload=Rcoil)时，输出功率达到最大值。

在实际工程结构中，当受到的激励振幅不断变化时，EIMD内部的振幅可能随不同的阻尼水平而变化，因此，使用阻抗匹配策略来最大化输出功率的方法不可靠，可通过将能量收集效率最大化来获得最大的输出功率。

能量收集效率η由式(4)表示

(3)

式中,cp为寄生阻尼系数。式(4)适用于适用于包括随机振动的一般振动情况。能量收集效率本质上是一个与频率和振幅相关的函数，当dη/dRload=0时，即Rload与最佳负载电阻相同时，能量采集效率η取得最大值ηmax。最佳负载电阻由式(5)表示

(4)

式(4)说明，可以通过增加负载电阻来增大能量采集效率η，但当负载电阻增大到最佳负载值时，继续增大会导致能量采集效率降低；增大齿轮转动比率ng，减小线圈电阻和寄生阻尼均可提高能量收集效率。

分析EIMD能量流动原理，发现其电能收集效率较高，Zhu等通过数值模拟验证出：当EIMD输入振幅为5 mm，频率为1 Hz正弦激励时，发电机输出功率为9.2 W，最大能量采集效率达到29.1%。在实际工程中，每布置一个EIMD，就相当于添加了一个小型电池。桥梁不断的受风荷载影响，直流发电机持续工作，能够做为桥梁上其他用电设备的供电源。并且拉索振动频率越大，发电机输出功率越大，若搭配其他种类电磁黏滞型阻尼器，与EIMD间隔布置，在台风等极端天气条件下，能够发挥高效的振动控制能力。

2 拉索的非线性运动方程

2.1 建立非线性运动模型

基于D’Alembert原理,将带有阻尼器的斜拉索自由振动方程建立在一个以弦长方向为x轴，以斜拉索的重力方向为y轴的局部坐标系上，如图4所示。假设斜拉索质量沿长度分布均匀，且具有相同的横截面。由于斜拉索柔性较大，在工程误差允许范围内忽略抗弯刚度对拉索垂度的影响(对于短索和大直径索，以及需要计算高阶模态时，抗弯刚度不可忽略)，忽略拉索自身纵向惯性力和阻尼力，以及外部动态荷载，带有阻尼器的斜拉索非线性运动方程可以表示为

(5)

(6)

(7)

式中：H和h分别表示沿x轴方向上的静态和动态张力分量;w和v分别表示相对于拉索静态平衡位置沿平面内和平面外运动的位移分量;u为轴向位移分量。Fdy和Fdz表示阻尼器固定位置的x轴坐标为xcj时，阻尼器沿y轴和z轴产生的阻尼力分量，l为拉索长度，δ表示狄拉克的三角形函数。m为每单位长度的拉索质量，c1和c2是斜拉索平面内和平面外内部阻尼系数，θ为拉索相对于水平平面的角度，如图3所示。z0为用抛物线近似微斜索静态平衡曲线，由式(8)表示。E为杨氏模量，A为拉索横截面面积，Le表示拉索有效长度。

(8)

图4 带有电磁调谐质量阻尼器的倾斜下垂拉索示意图

边界条件表示为[18]

u(0,t)=u1(t),u(l,t)=u2(t)

(9a)

w(0,t)=w1(t),w(l,t)=w2(t)

(9b)

v(0,t)=v1(t),v(l,t)=v2(t)

(9c)

将位移分量w、v、u用静态位移与动态位移之和表示为[18]

u(x,t)=us(x,t)

w(x,t)=ws(x,t)+wd(x,t)

v(x,t)=vs(x,t)+vd(x,t)

(10)

式中：us(x,t)、ws(x,t)、vs(x,t)表示满足边界条件的静态位移;wd(x,t)、vd(x,t)表示满足均匀边界条件的剩余动态位移。

拟静态位移表达式写为[19]

(11a)

(11b)

(11c)

将式(10)、(11)代入式(5)、(6)、(7)，忽略静态时拉索自身阻尼引起的阻尼力，式(5)、(6)、(7)写为

(12)

(13)

(14)

拉索有效长度Le近似表示为

(15)

f表示拉索跨中垂度，表达式为

(16)

2.2 简化模型

为了方便求得非线性微分方程组的数值解，将拉索平面内外动态位移分量用有限级数近似表示为

(17)

式中：pj(t)、qj(t)为广义位移;φj(x)为形状函数。Johnson等[20]提出了一种基于阻尼器位置的静态单元力引起偏转的形状函数

(18)

式中：φ1是由静力引起的阻尼器位置的标准化偏转;φ2是张紧拉索的平面外第一模态形状函数。将式(17)、(18)代入式(12)、(13)、(14)，使用标准伽辽金(Galerkin)方法，在式左右两边同乘以φi(x)并沿索长积分，忽略索内外平面运动相互影响，即式中二次和三次项，最终化简为

(19)

式中,(·)表示对时间t的偏导数，其他参数分别为

(20)

{P}=[p1p2q1q2]T,{d}=[l/2 2l/π 0 0]T

(21)

2.3 阻尼力

式(1)表示了电磁调谐质量阻尼器的力学模型，相较与由惯性质量、电磁阻尼所产生的阻尼力，寄生阻尼项中的库伦摩擦力产生的阻尼力很小，为简化模型，本文接下来的计算中省略库伦摩擦力fc。式(1)简化为

(22)

y为EIMD杆端位移，对斜拉索进行几何分析，如图4所示，得到以下几何关系式

平面内：y=1/cosγwd

(23a)

平面外：y=1/sinγvd

(23b)

将式(17)、(18)、(23)代入式(22)，计算得到基于阻尼器位置的阻尼力表达式为

(24a)

(24b)

在式左右两侧同乘以φi(x)并沿索长积分，化简计算得到

(25)

(26)

将式(25)、(26)代入式(19)，即可求得{P}。求解后，拉索跨中的平面内和平面外位移分别表示为

(27)

3 数值模拟

以某丹麦桥梁为例，进行数值模拟计算，验证运动方程的正确性。

斜拉索刚度为EA=2.17×109N，静态张力H=5.5×106N，索长260 m，每米索重81.05 kg/m，倾角θ=30.4°；平面内外索内部阻尼系数c1、c2由式(28)表示，其中平面内外模态阻尼比ξ均为1.0%，平面内外低模态圆频率ω1取3.201，ω2取3.148。

c1=2ξω1m,c2=2ξω2m

(28)

阻尼器安装位置为(l-xcj)=l/30，阻尼器工作倾角γ=45°，α=59.6°(根据Xu等[21]选择角度α=59.6°时，阻尼器的阻尼力垂直于倾斜拉索的弦线，可视为阻尼力的最佳方向)。

EIMD各项参数数据如表1所示。将各项参数代入式(19)，搭建Simulink动力仿真模型，计算初速度为0，平面内初位移为0，平面外初位移由于受到拉索垂度影响，以式(29)计算，取值为0.052 99。

vi∕t=0=vd,i∕t=0=dmssin(πx/l)

(29)

式中，dms表示拉索跨中处静位移，通常取值为1。

表1 EIMD各项参数表

求得方程的数值解，可得斜拉索平面内外位移如图5所示。图中振动曲线是由计算过程中迭代到每个时间节点时，拉索跨中位移所组成。整个振动过程中，平面内外位移均呈逐渐增大的趋势，本文为方便说明，取振动过程中时间间隔为70～100 s为例。

在图示时间段内，原索振动时，70～100 s内拉索平面内振动位移最大值为447.28 cm，平面外振动位移最大值为1 801.90 cm，安装ELMD后，平面内振动最大位移为119.31 cm，降低了73.3%;平面外振动最大位移为494.86 cm,降低了72.5%；同时，安装阻尼器后，随着时间的增长，平面内外振动位移增幅明显减缓。表明：电磁惯性质量阻尼器对拉索平面内外振动都有很好的抑制效果，拉索减振效果明显。

4 斜拉索垂度对EIMD振动控制效果的影响

根据拉索振动理论，斜拉索的垂度对阻尼器振动控制效果影响显著，为了获得拉索垂度影响效果的直观表现，基于D’Alembert原理,建立斜拉索-EIMD的线性运动方程。

4.1 建立线性自由振动方程

由式(6)可知，平面外非线性运动方程中不包含带有斜拉索垂度项z0，在接下来的分析中，只针对平面内振动的情况计算。忽略抗弯刚度，拉索自身阻尼和二阶小量h∂2w/∂x2的影响，由式(5)可得拉索平面内线性运动方程

(30)

忽略非线性项，即只考虑一阶的影响，由式(14)得：

(31)

引入反映拉索弹性H/EA及几何特性mgcosθl/H的Irvine参数λ2，即式(32)，由线性振动理论可知，拉索张力H越小，λ2越大，表明拉索垂度越大。

(32)

为得到运动方程的解析解，将拉索平面内位移分量w(x,t)近似表示为[22]

(33)

将式(31)、(15)、(16)代入式(30)后，以式(32)、(33)化简得到斜拉索-EIMD线性平面内运动方程为

(34)

式中，ω表示拉索振动圆频率。

4.2 阻尼器线性力学方程

在线性条件下，忽略库伦摩檫力，将式(1a)中的寄生阻尼项用线性的方法重新表示，电磁惯性质量阻尼器的力学模型可以简化为

(35)

线性寄生阻尼系数用cp表示

cp=cm+4fc/πωd

(36)

总阻尼系数用cd表示

(37)

将式(33)、(23a)代入式(35)，化简得到：

(38)

4.3 方程的解

将式(38)代入式(34)，斜拉索-EIMD运动方程可化简为

(39)

式中：β表示波数;η为阻尼器阻尼系数;表达式分别为

(40a)

(40b)

(41)

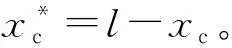
式(41)包含了两种三角函数，分别对应近似反对称振动模式和近似对称模式振动两种情况，如图6所示。

(a) 近似反对称振动模式

4.4 近似对称振动

4.4.1 波数方程

去掉波数方程(41)中，与近似反对称振动模态相关的解，即方程左右两侧同除以sin(βl/2)，整理得到近似对称模式的近似波数方程如式(42)所示。

(42)

(43a)

(43b)

4.4.2 近似对称模式的双参数渐进

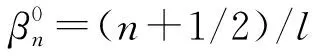
(44)

将式(44)代入式(42)，并以无阻尼波数计算式(42)右侧时，可得复波数增量表达式为

(45a)

(45b)

特征频率ωn与阻尼比的关系如下

(46)

下角标n表示模态数。第n个模态阻尼比ζn可以表示为

(47)

根据双参数渐进公式整理得到对应的模态阻尼比表达式如下

(48)

当斜拉索没有设置阻尼器时，近似对称模式的波数方程(41)左侧第二个因子确定。整理后，可得

(49)

式(49)为关于振动频率的超越方程，解为正切函数与三次函数的图像交点，根据线性振动理论，式(49)解得的频率值在λ2=(n+1)2π2时，出现模态跳跃的分界点，拉索振动固有频率在分界点两侧呈现不同的变化规律，Krenk等中将这种现象称作频率交叉，即对应图6(b)的振动情况。Krenk等计算得到出现频率交叉现象时，波数的对应取值为：βnl=βn+1l=(n+1)π。图6(b)上侧表示λ2小于频率交叉点值，这种情况下，拉索振动位移w(x)符号保持不变；当λ2大于频率交叉点值时，拉索振动位移w(x)在对称的两个点出现了符号改变，如图6(b)下侧所示。在交叉点前后，振型曲线在对称模式与反对称模式间振荡，因此，可将λ2在频率交叉点的值看作临界值。

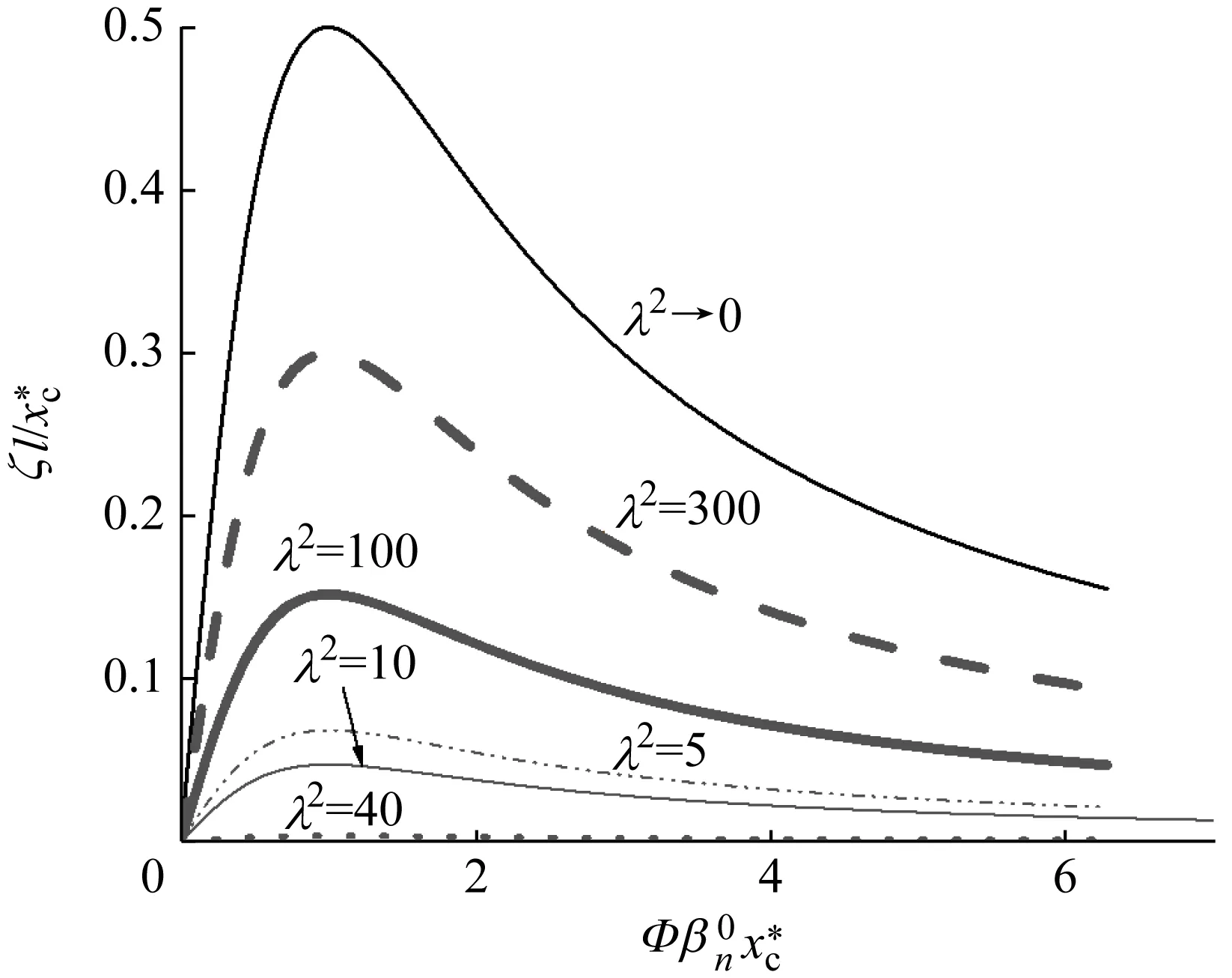
图7 n=1且时阻尼比ζn

4.5 近似反对称振动

4.5.1 波数方程

去除式(41)中与近似对称模式相关的根，即方程左右两边同除以cos(1/2βl)项，整理得到近似反对称模式的波数方程

(50a)

(50b)

Irvine等[24]提出可以在正切函数的分支上找到式(50)的近似解即式(51)。

n=2,4,…

(51)

(52)

4.5.2 近似反对称模式的双参数渐进

(53)

n=2,4,…

(54)

将式(54)代入式(47)可得

(55)

图8 n=1且时阻尼比ζn

将Φ中的阻尼器参数归一化处理后，代入式(48)及式(55)，进行EIMD的惯性质量和阻尼系数分析。由于EIMD的力学模型经线性化处理后与惯性质量阻尼器(IMD)相似，从而EIMD参数分析可参照Wang等对IMD参数的分析过程。

5 结 论

(1) 本文通过求解EIMD与斜拉索共同作用的非线性自由振动方程，得出斜拉索振动位移-时间曲线，验证了电磁惯性质量阻尼器对抑制斜拉索平面内外振动位移的有效性。计算得到在70～100 s时间段内，安装EIMD后平面内振动位移由447.28 cm降至119.31 cm，降低73.3%，平面外振动位移由1 801.90 cm降至494.86 cm，降低72.5%，从理论上证明了EIMD的减振性能优越。

(2) 通过建立求解斜拉索-EIMD的平面内振动线性自由振动方程，得出：① 近似对称模式下，拉索垂度对阻尼器的控制效果影响明显。在低阶模态下，当λ2小于临界值4π2=39.478时，阻尼器的控制效果随着垂度逐渐增大而降低，当λ2大于临界值时阻尼器的控制效果随垂度增大而增大；② 近似反对称模式下，拉索垂度对阻尼器的控制效果没有影响。

EIMD具有良好的减振性能和可自发电的特性，在应对极端大风天气或自然灾害时，能够在正常工作的同时输出电能；在桥梁抗风设计时，可与电磁黏滞型阻尼器间隔布置，两类阻尼器共同工作，既能最大限度的控制桥梁振动，也能够很好的解决电磁黏滞型阻尼器野外持续供电的难题，在桥梁上的应用前景广泛。