行波激励下高烈度区特大铁路悬索桥减震技术研究
宋光松,江辉,郭辉 ,陈良江,卢文良,周勇政,何友娣
(1.北京交通大学 土木建筑工程学院,北京 100044;2.中国铁道科学研究院集团有限公司,北京 100081;3.高速铁路轨道技术国家重点实验室,北京 100081;4.中国铁路经济规划研究院有限公司,北京 100038;5.中铁大桥勘测设计院集团有限公司,湖北 武汉 430056)
悬索桥跨越能力强、受力明确、布局合理,已成为大跨桥梁的主力桥型之一,由于其支承距离大,地震波的长距离传播,使不同支承点在同一时刻所受地震激励差异较大,行波效应的影响不可忽视[1]。国内外学者对行波激励下悬索桥的地震响应开展了系列研究。一些学者研究得出,行波效应会对结构响应产生不利影响。ADANUR等[2−3]以博斯普鲁斯海峡悬索桥为对象,指出行波效应会增大桥塔响应。闫聚考等[4]指出,行波效应会导致泰州长江大桥塔顶位移、塔梁相对位移、主桥及引桥相对位移增大。而另一些学者则发现行波效应对结构的响应是有利的。苗润池[5]研究表明,行波激励下伍家岗长江大桥的响应小于一致激励。宋旭明等[6]指出,行波效应可使湘江三汊矶大桥的横向弯矩减少60%,纵向位移及塔底内力减少10%左右。此外,WANG等[7]认为,行波效应对桥梁地震响应的影响具有波动性,受结构特性、地震波特性和传播方向等多因素影响。为有效控制大跨度悬索桥的地震响应,不同学者对其减震技术也进行了研究。VADER等[8]以奥克兰海湾大桥为对象得出,摩擦型阻尼器可有效降低桥塔纵向响应。ZHENG等[9−12]指出,黏滞阻尼器及软钢阻尼器均可有效控制悬索桥的主梁位移,但钢阻尼器会增大桥塔内力。此外,GUO等[13−14]得出,耗能型中央扣可明显改善悬索桥桥塔的抗震性能,弹性索可有效控制塔梁相对位移,但会增大塔底剪力与弯矩。综上,行波效应对悬索桥地震响应的影响十分复杂,结论尚未统一,减震技术的研究也未充分考虑行波效应的影响,且相关成果主要集中于公路悬索桥。铁路悬索桥恒载较公路桥更大,同条件下的地震响应更大,对结构的抗震设计也提出了更高的要求。为此,本文以我国高烈度区某千米级跨径铁路悬索桥为对象,开展行波激励下桥梁地震响应特性及减震技术研究,相关成果可为同类型桥梁的抗震设计提供参考。
1 工程背景及有限元模型
某大跨度铁路悬索桥,其桥位处为高山峡谷“V”型地貌,周围分布有多个强地震带,地震基本烈度达到Ⅷ度,Ⅱ类场地,基本地震动峰值加速度为0.30g,反应谱特征周期0.6 s。该桥采用设计地震(中震)、罕遇地震(大震)两水准抗震设防,总体目标是“中震不坏、大震可修”。
该桥为主跨1 060 m的钢桁梁铁路悬索桥(图1),桥塔为钢筋混凝土结构,其中东侧桥塔高262.8 m(以下简称“东塔”),西侧桥塔高145.8 m(简称“西塔”),主梁采用上承式钢桁梁,主缆由镀锌高强钢丝(抗拉强度2 100 MPa)制成,吊杆由高强钢丝(抗拉强度1 770 MPa)制成,主缆与主梁在跨中位置通过柔性中央扣联结,材料与吊杆一致。全桥支座采用球形钢支座,具体布置情况如表1所示。

图1 桥梁立面布置示意图Fig.1 Schematic diagram of the bridge elevation layout

表1 球形钢支座布置情况及力学参数Table 1 Layout and mechanical parameters of spherical steel bearings
基于Midas Civil有限元软件建立全桥计算模型(图2),主梁、桥塔采用梁单元模拟,主缆、吊杆、柔性中央扣采用桁架单元模拟,桥面板通过板单元模拟。表2给出了模型边界及连接条件,其中0表示自由,1表示主从连接或固结,S表示弹簧约束;X,Y,Z,θx,θy和θz分别为纵桥向、横桥向、竖向平动自由度与转动自由度。主缆端部固结以模拟隧道锚的约束作用,主缆散索鞍除纵向平动自由度外,其余按固结处理,主缆与桥塔、主梁与桥面板均采用刚臂连接,桥塔桩基处通过6弹簧模型模拟土−结相互作用。此外,横向抗风支座、竖向支座采用双线性模型模拟,具体参数设置见表1。

表2 模型边界及连接条件Table 2 Boundary and connection conditions of the model

图2 全桥结构有限元模型Fig.2 Finite element model of the bridge structure
桥梁初始线形考虑主缆、吊杆、主梁自重及二期恒载,并以均布荷载(q=447.18 MN/m)施加于桥面系。经成桥分析,主缆、吊杆、主梁、桥塔初始内力峰值响应分别为337.05,2.70,302.20和754.28 MN,与相关设计单位的结果吻合良好。计算该桥的自振特性得出,桥梁1阶周期为10.22 s,1阶振型为主梁对称横弯。经调研可知,公路、铁路悬索桥1阶振型均以主梁横弯为主;跨径相近的情况下,由于铁路悬索桥主梁及桥塔通常具有较大刚度与较高基频,其自振周期较公路桥有所减小。该桥自振特性符合悬索桥周期、振型分布规律,可较好验证模型的合理性。
2 地震动的选取与输入
根据桥梁场地特征及设计反应谱曲线,在太平洋地震工程研究中心NGA-West2数据库按照下述标准选取地震动:1) 断层距小于15 km;2) 剪切波速为250~500 m/s;3) 基于双频段法[15]控制所选地震动均值谱与设计谱相匹配。最终所选取的地震记录的基本信息见表3。
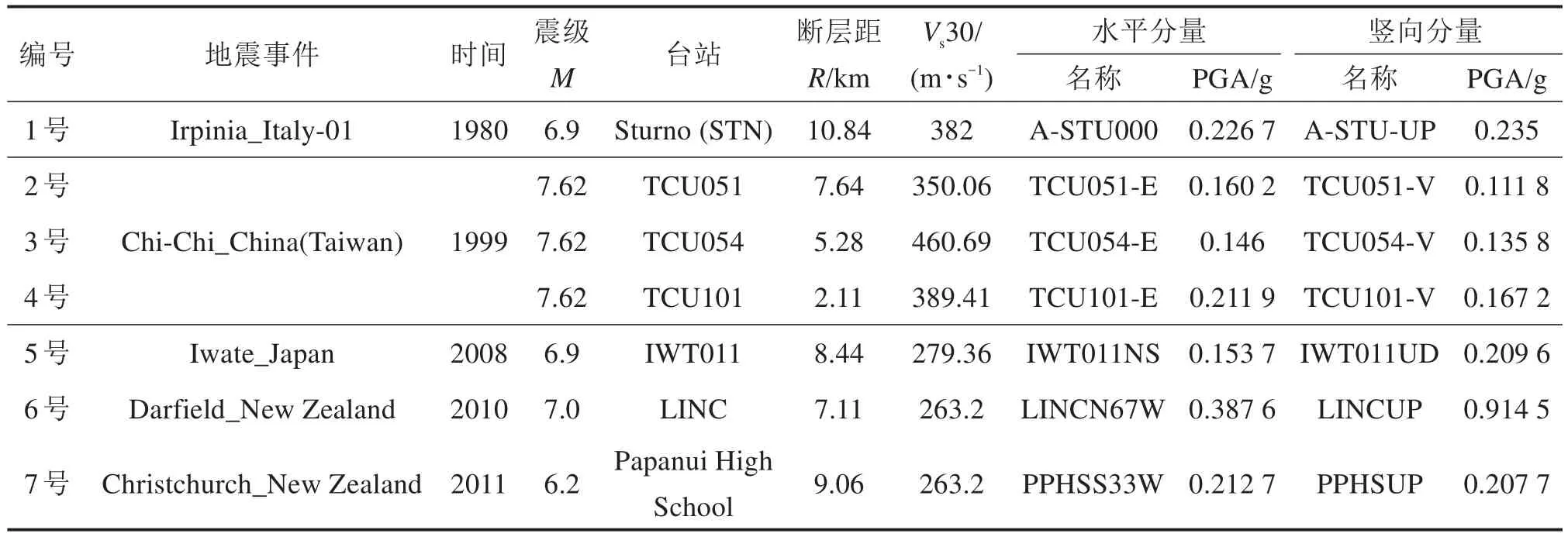
表3 所选地震动记录基本信息Table 3 Basic information of selected ground motions
目前多点激励分析方法主要包括相对运动法及大质量法,前者基于叠加原理,只适用于线弹性体系;大质量法可实现复杂结构的非线性分析,应用更广泛,因此本文选用此方法进行多点激励地震动的输入。
大质量法原理为:释放结构基础或支撑点地震激励方向的约束并施加大质量块M0(一般取结构总质量的106倍),在大质量点施加动力时程M11模拟地震加速度(图3),其本质是一种近似解法[16],为有效降低瑞利阻尼所带来的地震动输入误差,本文对加速度时程进行修正[17]:

图3 大质量法模型示意图Fig.3 Schematic diagram of the Large Mass Method model

式中:为修正后的加速度时程;和为修正前加速度和速度时程;α为瑞利阻尼的相关系数。
根据结构基础及支撑点,选取A,B和C(西侧锚碇、桥台、桥塔桩基)及D,E和F(东侧桥塔桩基、桥台、锚碇)作为地震动输入点,如图4所示。

图4 地震动输入点示意图Fig.4 Schematic diagram of ground motions input points
3 地震响应特性
本文算例桥梁位于近断层高烈度区,需考虑竖向地震作用。由于近断层地震通常具有较大的竖向加速度幅值,结合场地特征和安评规定,本文所取竖向加速度峰值与水平向一致。
将水平向和竖向加速度时程调幅至罕遇地震水平,输入结构开展时程计算,分析视波速及传播方向对桥梁地震响应的影响。传播方向1为东―西侧,方向2为西―东侧。考虑场地剪切波速及便于与一致激励对比,视波速最小取250 m/s,最大取8 000 m/s,共设置7种波速(250,500,750,1 000,2 000,4 000,8 000 m/s),一致激励下波速为∞。
图5(a)~5(b)为行波激励下梁端位移的分布,可见,随视波速增大,位移总体先下降后上升,当视波速为250 m/s及500 m/s,以方向2传递时,东侧位移响应较一致激励有所增大,其余工况则有所降低,最大降幅为59.49%;西侧规律相似,最大降幅为64.20%。塔顶位移则随视波速的增大先下降后趋于平稳(图5(c)~(d)),其响应值总体较一致激励有所增大,东塔和西塔的最大增幅分别为90.98%和116.06%。

图5 不同视波速下梁端位移、塔顶位移及中央扣应力分布Fig.5 Distributions of girder end and tower top displacements, central buckle stresses at different apparent wave velocities
由图5(a)~(d)还可看出,视波速较小时,行波效应对远波源侧的梁端、塔顶位移响应更不利,视波速较大时则对近波源侧更不利。WANG等[7]也指出,视波速较大时,泰州长江大桥距震源较近的桥塔内力及塔梁相对位移均大于远震源侧。因此,在桥梁抗震设计中,鉴于地震传播方向的不确定性,需考虑其对结构位移响应的影响。
此外,如图5(e)所示,行波激励下,柔性中央扣应力随视波速的增大呈“增大−下降−增大”趋势,其响应较一致激励均有所降低,最大降幅达63.34%,但仍超出限值(1 770 MPa)。由于主梁的地震惯性力通过中央扣传递至主缆,铁路悬索桥主梁刚度、质量更大,其中央扣较公路桥更易被破坏。
图6给出了东塔和西塔弯矩的分布,可看出,其响应峰值均出现在塔底位置。随视波速的增大,东塔塔底弯矩总体逐渐增大,西塔则呈震荡变化。相较一致激励,行波效应对东塔塔底弯矩以有利影响为主,响应最大降幅为41.24%;对西塔则以放大效应为主,响应最大增幅为46.51%。

图6 不同视波速及传播方向下桥塔弯矩分布Fig.6 Distributions of tower bending moments at different apparent wave velocities and directions
以LINCN67W地震波为例,图7为东塔塔底弯矩的时程曲线。研究发现,传播方向一定,视波速为250,500和2 000 m/s时,其弯矩峰值为4 473,6 473和9 337 MN∙m,出现时刻为31.88,30.12和29.08 s;而视波速一定时,方向1和2峰值响应分别为6 473 MN∙m和6 667 MN∙m,出现时刻为30.12 s和33.56 s。可见,视波速主要影响弯矩峰值大小,而传播方向主要影响其出现时间。其他地震波规律相似,此处不再赘述。

图7 东塔塔底弯矩时程曲线Fig.7 Time history curves of bending moments at the bottom of the east tower
通过以上分析可知,行波激励下结构的响应分布十分复杂,随视波速的增大,其变化趋势并不一致且均未呈现严格的单调变化特征,尤其视波速为750,1 000和2 000 m/s时,响应变化幅度大且无明显规律,此特殊现象可采用行波共振理论解释[17−18]。
行波共振是指当结构的跨度接近于其自振频率所对应激励波长的一半时,使得一致激励下对结构地震反应贡献为0的振型处于共振状态,从而对响应贡献最大化的现象。
以该桥桥塔桩基处为例,假设输入正弦波,其频率与桥梁各阶自振频率fi相同,则波长λi为:

其中,v为视波速。一致激励下,纵向地震为反对称输入,对称振型对结构响应无贡献。如图8所示,如果存在某特定视波速使桥梁主跨度接近于激励波长的一半,那么两桥塔地震动输入大小相等、方向相反,从而形成对称激励,若此时振型为对称振型,则会产生行波共振,使该阶振型的贡献最大化。

图8 行波共振示意图Fig.8 Schematic diagram of the traveling wave resonance
表4给出了桥梁跨度与各阶振型激励波长的关系,可看出,视波速为750,1 000和2 000 m/s时均会发生行波共振现象。由于各阶振型反应叠加时存在方向组合的问题,相较一致激励,行波共振可能使结构响应大幅度增大或减小,而在视波速500~750 m/s区间内其变化幅度最大,这是由于低阶振型贡献较高阶振型更大,对结构的影响也更大。

表4 悬索桥跨度与各阶振型激励波长的关系Table 4 Relationships between the span of suspension bridge and modes of vibration’s wavelength
楼梦麟等[17,19]同样指出,对于大跨度拱桥和斜拉桥,特定视波速下同样会发生行波共振现象,从而造成结构响应的大幅度变化。因此,这一现象需在大跨度桥梁抗震设计时格外关注。
4 行波激励下减震技术研究
为充分考虑行波激励对结构抗震设计的不利影响,结合桥梁各关键构件的地震响应,选取视波速500 m/s,传递方向1的行波激励开展减震研究。此时,柔性中央扣应力(5 988 MPa)及梁端位移(东侧1 358 mm,西侧1 518 mm)已超出设计限值。经调研,目前悬索桥常用的减震、限位装置主要包括阻尼器(黏滞阻尼器、钢阻尼器、磁流变阻尼器等)、中央扣(刚性中央扣、柔性中央扣、耗能型中央扣)及弹性索。相较于黏滞阻尼器及钢阻尼器,磁流变阻尼器造价昂贵,控制算法复杂;弹性索多用于多塔悬索桥以限制结构的主梁纵向位移;耗能型中央扣具有支撑与耗能的双重作用,减震效果更好。本文重点分析耗能型中央扣、E型钢阻尼器、黏滞阻尼器及其组合对桥梁地震响应的影响规律及减震效果。
4.1 耗能型中央扣
耗能型中央扣通常由防屈曲支撑制成,多遇、设计地震下可提供刚度,起约束限位作用,罕遇地震下发生塑性变形从而耗散地震能量,其滞回模型如图9所示,图中,k,Fy,Fmax,dy和dmax分别为弹性刚度、屈服强度、极限承载力、屈服位移和极限位移,在Midas Civil中可近似采用双线性模型模拟。本节分析了中央扣布置对数(2,3和4对)及屈服强度[13,20]对桥梁地震响应的影响,其力学参数如表5所示。

图9 耗能型中央扣滞回模型Fig.9 Hysteresis model of energy-dissipating central buckles

表5 耗能型中央扣关键力学参数Table 5 Key mechanical parameters of energy-dissipating central buckles
图10(a)~10(b)为不同屈服强度下中央扣滞回曲线及内力的分布,可看出,曲线形状饱满,中央扣性能稳定,耗能良好。通过调整耗能型中央扣的布置对数及屈服强度,可保证其内力响应低于极限承载力,进而解决高烈度区柔性中央扣破坏的问题。为充分发挥其耗能性能且不失效,建议在主梁跨中布置3对屈服强度10 MN的耗能型中央扣。
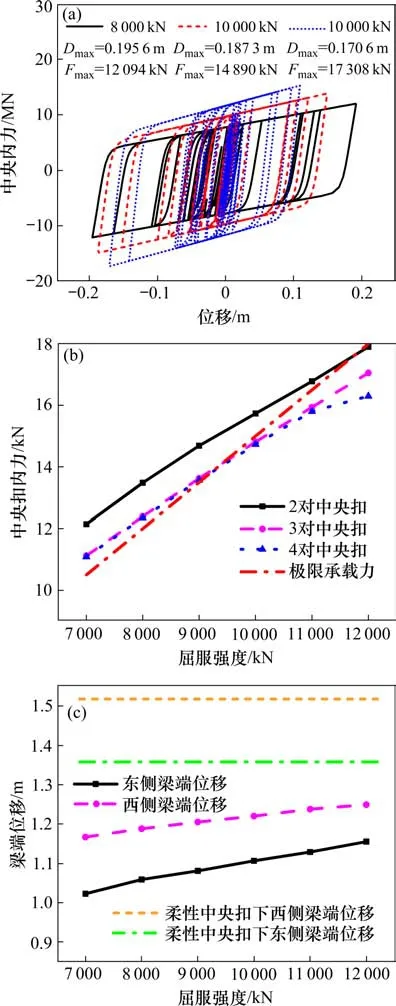
图10 不同屈服强度下中央扣响应及梁端位移分布Fig.10 Distributions of central buckle responses and girder end displacements at different yield strengths
以布置3对中央扣为例,图10(c)给出了不同屈服强度下梁端位移的分布。相较于柔性中央扣,耗能型中央扣可有效降低梁端位移,东侧、西侧的最大降幅可达24.70%和23.11%,但仍超出梁台间隙(1 m)。
4.2 耗能型中央扣+E型钢阻尼器
由4.1节可知,单独布置耗能型中央扣时梁端位移超限。既有研究表明,E型钢阻尼器可有效控制结构的位移响应,其滞回模型如图11所示,图中D1,D2,K1,K2,F1和F2分别为屈服位移、极限位移、弹性刚度、屈服后刚度、屈服荷载和极限荷载,在Midas Civil同样可采用双线性模型模拟。

图11 E型钢阻尼器滞回模型Fig.11 Hysteresis model of E-shaped steel dampers
本节在塔梁、台梁连接处加设一个参数相同的E型钢阻尼器,分析屈服荷载对结构响应的影响及“耗能型中央扣+E型钢阻尼器”的减震效果,所选用阻尼器的屈服位移取10 mm,极限位移取屈服位移的15倍,极限荷载取屈服荷载的1.15倍[12,21],所设工况的具体力学参数如表6所示。

表6 E型钢阻尼器关键力学参数Table 6 Key mechanical parameters of E-shaped steel dampers
研究表明,梁端位移随屈服荷载的增大逐渐降低(图12(a)),较仅布置耗能型中央扣,加设E型钢阻尼器可使东侧和西侧位移响应分别降低68.00%和73.03%,但其对塔顶位移的减震效果并不显著,且由于桥梁刚度的增加,桥塔轴力有所增大,最大增幅为5.98%。此外,如图12(b)所示,阻尼器位移随屈服荷载的增大逐渐降低,但东侧台梁连接处最小响应为167.88 mm,仍超出极限位移(150 mm),阻尼器已失效。

图12 不同屈服荷载下梁端位移、阻尼器位移响应分布Fig.12 Distributions of girder end and damper displacements at different yield loads
4.3 耗能型中央扣+黏滞阻尼器
4.2节研究表明,E型钢阻尼器可控制梁端位移,但会造成桥塔轴力的增大与阻尼器的失效。黏滞阻尼器是一种速度型阻尼器,不会增加结构刚度与受力,在动力时程分析中可采用Maxwell模型模拟。该模型由阻尼器单元、弹簧单元串联而成,力-变形公式与示意图如式(3)和图13所示。

图13 Maxwell模型示意图Fig.13 Schematic diagram of the Maxwell model
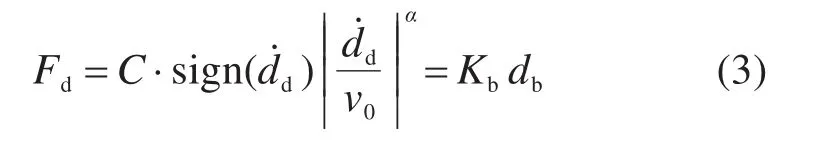
式中:Fd,dd,C和α为阻尼器阻尼力、阻尼位移、阻尼系数和阻尼指数;v0为参考速度;Kb和db为弹簧刚度与位移;sign(·)为符号函数。
分别在相同位置布置黏滞阻尼器,分析得到了阻尼系数和阻尼指数对结构地震响应的影响及组合减震措施的减震效果。阻尼器具体力学参数如表7所示,共设置25组工况。
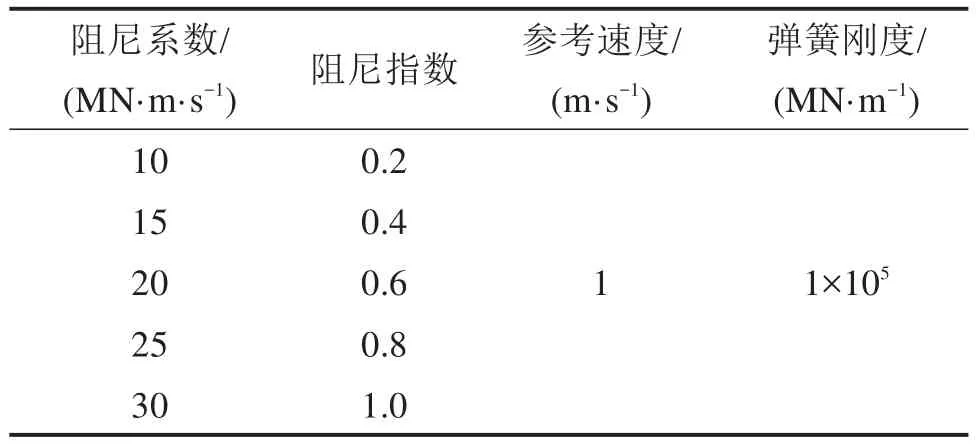
表7 黏滞阻尼器关键力学参数Table 7 Key mechanical parameters of viscous dampers
以东侧梁端位移为例,不同阻尼参数下的位移响应分布如图14(a)所示,可看出,位移响应随阻尼系数的增大不断降低,随阻尼指数的增大逐渐增大。西侧变化趋势一致,此处不再赘述。通过阻尼器的滞回曲线可以较好解释此现象。如图15所示,阻尼指数一定时,曲线面积随阻尼系数的增大而增大,因此耗能量增大,梁端位移降低;而阻尼系数一定时,曲线形状随阻尼指数的增大逐渐由矩形变为椭圆形,耗能性能下降,位移增大。研究得出,较仅布置耗能型中央扣,组合减震措施可使西侧和东侧梁端位移响应分别下降25.98%和26.24%。

图14 不同阻尼参数下梁端位移、塔底弯矩、阻尼器速度分布Fig.14 Distributions of girder end displacements, tower bottom bending moments, and damper velocities at different yield loads

图15 黏滞阻尼器滞回曲线Fig.15 Hysteretic curves of viscous dampers
以东塔为例,图14(b)给出了塔底弯矩的分布。不难看出,弯矩随阻尼系数的增大逐渐降低,而阻尼指数的影响并不显著,最大变化幅度仅为2.71%。由于黏滞阻尼器可大量消耗地震输入能量,相较单独布置耗能型中央扣,组合减震措施可有效降低东塔塔底弯矩,最大降幅为26.10%。
需注意的是,如图14(c)所示,当阻尼系数为10 (MN∙m)/s和15 (MN∙m)/s时,由于阻尼器自身耗能能力有限,无法承受罕遇地震力作用,其速度响应已超出设计限值。综合考虑桥梁各构件响应及减震设计的安全性和经济性,建议该桥采用阻尼系数为20 (MN∙m)/s和阻尼指数为0.2的黏滞阻尼器。
5 结论
1) 行波效应对桥梁响应的影响十分复杂;随视波速的增大,梁端位移先下降后增大,塔顶位移逐渐减小后趋于稳定,东塔塔底弯矩不断增大,而西塔塔底弯矩则呈震荡变化。相较一致激励,行波效应可使梁端位移、东塔塔底弯矩下降64.20%和41.24%,使塔顶位移和西塔塔底弯矩增大116.06%和46.51%。
2) 视波速较小时,行波传递方向对远波源侧梁端、塔顶位移响应更不利,视波速较大时则相反。鉴于实际地震动传播方向的不确定性,需考虑其对桥梁响应的影响。
3) 特定视波速(750,1 000和2 000 m/s)下悬索桥会发生行波共振现象,此时各构件响应的变化幅度更大,由此造成的不利影响需在大跨度桥梁抗震设计时格外关注。
4) 对于铁路悬索桥,布置耗能型中央扣可解决高烈度区柔性中央扣破坏的问题,加设E型钢阻尼器可使梁端位移下降73.03%,但会造成桥塔轴力的增大与阻尼器的失效;“耗能型中央扣+黏滞阻尼器”的组合措施可同时降低结构的位移及内力响应,更适用于高烈度区大跨度铁路悬索桥的减震控制。
5) 考虑结构响应及减震设计的安全性、经济性,推荐主梁跨中布置3对屈服强度为10 MN的耗能型中央扣,塔梁、台梁连接处布置阻尼系数为20 (MN∙m)/s,指数为0.2的黏滞阻尼器。对于同类桥梁,所采用耗能装置的规格可能有所不同,但组合使用位移型、速度型减震技术的设计思路可供参考借鉴。
需说明的是,对于高烈度峡谷区大跨度桥梁,局部场地及部分相干效应的影响同样不可忽视。本文作者研究发现,当同时考虑多种地震动空间效应时,由于场地、地震动和结构等多因素的交叠影响,其响应完全呈波动分布,难以分析和提炼规律性认识,后续作者将对此开展更深入的研究。

