TBM刀盘裂纹分析及止裂方案研究
刘建琴 ,郭晓,闫康伟,安蔚瑾,宋欣
(1.天津大学 机械工程学院,天津 300350;2.天津农学院 工程技术学院,天津 300384)
据统计,工程结构在服役期间的失效约90%是由疲劳引起的,疲劳裂纹的萌生和扩展是工程结构失效的主要原因[1]。裂纹作为常见的一种缺陷,如果萌生以后不加以处理,将会迅速扩展,降低构件强度和使用寿命,甚至造成更大损失。所以,对裂纹止裂方案的研究具有重要的工程意义。在隧道掘进机(Tunnel Boring Machine, TBM)掘进过程中,刀盘系统位于掘进机的最前沿,承担破岩、稳定掌子面的任务。施工过程中刀盘系统要承受大扭矩、大推力和强冲击载荷作用,会出现滚刀严重磨损、刀盘开裂失效、刀盘盘体断裂失效等非常棘手且代价昂贵的工程问题,严重影响施工进度及工程成本。针对TBM刀盘刀具裂纹及寿命研究,欧阳湘宇等[2]根据数理统计理论拟合的幅值分布函数编制了应力程序谱,结合材料的S-N曲线和损伤累积准则预测了刀盘裂纹萌生寿命。刘建琴等[3]研究了地质匹配性因素对危险点裂纹萌生寿命的影响和失效区域性因素对危险点剩余裂纹萌生寿命的影响。朱晔[4]基于Newman模型及累积损伤理论,构建了疲劳裂纹扩展寿命预测模型进行疲劳寿命预测,并用刀盘特征子结构进行了裂纹扩展的实验验证。ZHU等[5]基于断裂力学,结合裂纹的破坏方式和裂纹扩展的一般机理,建立了TBM刀盘全阶段裂纹扩展速率模型,并通过了实验验证。凌静秀等[6]采用基于子模型技术的有限元法,分析了复杂应力状态下刀盘裂纹的应力强度因子,并给出了不同裂纹参数对应力强度因子的影响规律,为刀盘裂纹扩展寿命的预测提供了输入条件。上述研究主要是对刀盘裂纹的萌生位置、萌生寿命以及扩展速率进行研究,但是未涉及刀盘裂纹扩展过程以及扩展后的裂纹止裂方法。在裂纹止裂及修复方法方面,工程上钢结构常用的方法有止裂孔法、补焊法和补强板法(钢板或CFRP)[7]。吉伯海等[8]研究了钢箱梁疲劳裂纹止裂孔的孔径、位置和角度等参数对止裂效果的影响。王秋东等[9]分析了不同补强筋板尺寸对裂纹尖端应力的影响,并对钢板补强维护效果进行了评价。朱晔[4]则通过分析具体施工案例,在刀盘结构内部设计加强筋板,从而提高刀盘内部结构的抗裂能力。上述工程上通用的几种止裂研究主要是针对三维贯穿裂纹的止裂,但是刀盘上的裂纹常位于表面,且裂纹深度相对于刀盘厚度较小,可看作表面裂纹。根据文献[10]可将刀盘表面裂纹简化为半椭圆裂纹处理,而目前学界对于表面半椭圆裂纹的研究较少,对TBM刀盘的止裂方案更是鲜有涉及。LI等[11]利用半椭圆裂纹模型对刀盘裂纹扩展进行了有限元仿真,并在仿真数据的基础上建立了刀盘疲劳寿命预测模型,但其对于裂纹扩展的有限元仿真仅限于数据收集层面,并没有进行裂纹规律的探索和止裂方案的研究。因此,本文针对TBM刀盘在破岩过程中出现的表面裂纹,建立刀盘裂纹扩展模型,用于模拟裂纹的开裂过程,并提出相应的止裂方案。同时,研究止裂筋板关键参数对于止裂效果的影响规律,并提出基于止裂系数的止裂效果评价方法。
1 裂纹扩展模型
1.1 刀盘子模型
选用辽宁大伙房水库输水隧洞项目所用TBM刀盘(MB264-311-8030mm)为研究对象。刀盘为中方五分式刀盘,刀盘材料为Q345,共51把滚刀,其中中心滚刀8把,正滚刀32把,边滚刀11把[12]。
在Abaqus中模拟滚刀破岩过程,以获取滚刀载荷的时间历程,将载荷历程取平均值,通过刀孔上的耦合控制点施加到刀盘模型上,获得刀盘的应力分布情况,如图1所示。
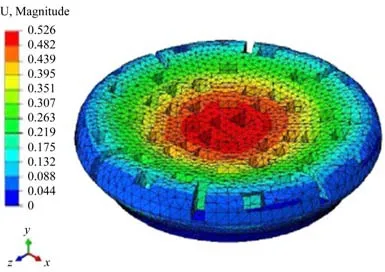
图1 TBM刀盘变形分布Fig.1 Deformation distribution diagram of the cutter-head
从图1中可知刀盘中心位置应力最大。结合文献[13]中刀盘危险区域的分区,从区域4中心块面板取一个子模型进行裂纹分析,如图2(a)所示。为提高计算效率,子模型参数如图2(b)所示。为模拟裂纹扩展阶段,在子模型中设置一条初始裂纹,假定初始裂纹半长c取10 mm,裂纹深度a取5 mm,如图2(b)所示。
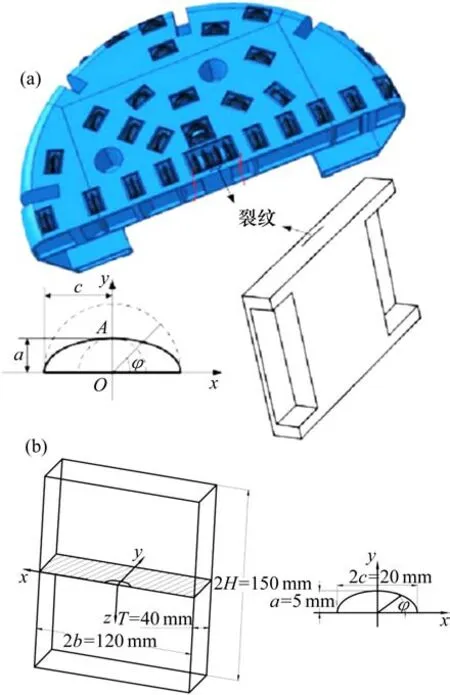
图2 刀盘子模型位置及形状示意图Fig.2 Location and shape of cutter-head model
1.2 裂纹扩展模型
目前,在疲劳裂纹扩展寿命预测方法的研究中,应用最广泛的仍然是Paris公式[14],相对于其他基于概率和断裂力学的“应力−寿命”模型,其与实际更加接近,模拟了缺陷引起的裂纹萌生和扩展机理,同时其也对材料参数的设置要求更严格[15−16]。Paris公式形式为:

式中:a为裂纹长度;N为应力循环次数;dadN为裂纹扩展速率;C和m为材料参数;ΔK为应力强度因子幅。

式中:Kmax为强度应力因子最大值;Kmin为强度应力因子最小值。
为便于Abaqus仿真分析,用能量释放率来代替强度应力因子,则Paris公式可以表示为:
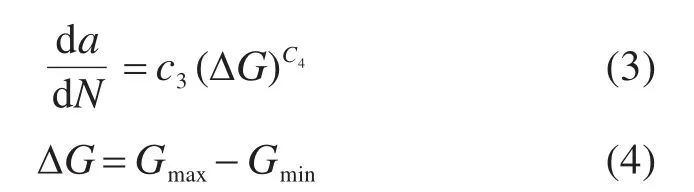
式中:ΔG为应变能释放率;Gmax和Gmin分别为结构中最大载荷和最小载荷对应的应变能释放率;参数c3和c4为材料参数。c3和c4主要由刀盘的材料参数C和m决定,其转换关系见文献[17]。
疲劳裂纹的萌生和扩展规律如图3所示,图中Gthresh为应变能释放率门槛值;Gpl为应变能释放率上限值;GC为临界应变释放率。Paris法则以Gthresh和Gpl为上下界,低于Gthresh疲劳裂纹不扩展,高于Gpl疲劳裂纹将快速扩展至破坏。介于Gthresh和Gpl的中间直线区域,是疲劳裂纹稳定扩展区域,也是Paris法则控制区域。
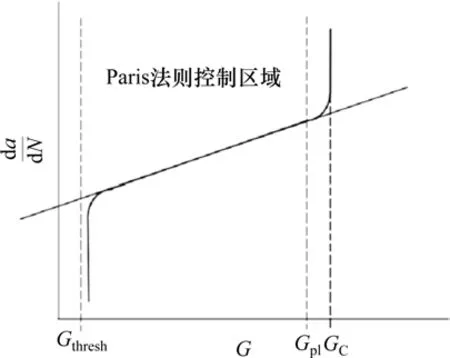
图3 疲劳裂纹的萌生和扩展规律Fig.3 Initiation and propagation of fatigue cracks
基于式(3),在Abaqus中仿真裂纹的扩展规律,通过关键字形式设置相应的材料参数建立裂纹扩展模型。表1所示为刀盘面板材料参数[18−19]。在模型中,加载载荷即可模拟裂纹的开裂过程并获取对应的载荷循环次数。

表1 刀盘面板材料参数Table 1 Material parameters of cutter-head
裂纹在网格中的扩展是利用扩展有限单元法(XFEM)[20−21]来实现的,其是一种新兴的数值计算方法,通过扩充位移项来描述不连续的位移场,使裂纹独立于网格存在,从而能够模拟任意形状的裂纹,克服了传统有限元在裂纹扩展过程中需要对裂纹尖端的网格进行重划分的缺点,能够降低网格划分要求,提高运算效率。
本文采用XFEM方法,实现对裂纹扩展路径和过程的仿真,即在Abaqus中将裂纹设置为XFEM形式。
2 止裂筋板设计及裂纹开裂仿真
2.1 止裂筋板设计
采用止裂筋板的方法进行裂纹止裂,即通过在裂纹两端焊接止裂筋板来改善应力分布,从而通过降低裂尖应力集中以达到延缓或抑制裂纹扩展的目的。
图4为止裂筋板的结构示意图,其中,L代表裂纹尖端距离筋板中心的长度,t代表筋板厚度,h代表筋板高度,W代表筋板宽度。筋板材料与子模型相同,均为Q345。
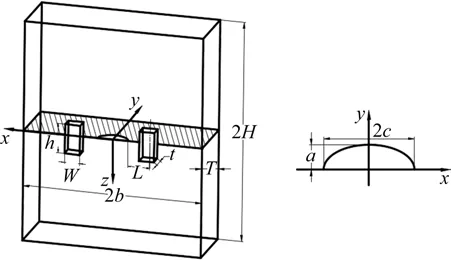
图4 止裂筋板的结构示意图Fig.4 Schematic diagram of crack-stopping stiffened plate
由于该子模型关于YZ平面对称,为了提高运算效率,取模型的一半进行分析,如图5所示,建立带筋板的裂纹扩展模型,图中凸起位置为止裂筋板。在刀盘子模型左侧YZ平面施加对称约束,仿真完成后镜像显示,则可以得到完整裂纹扩展模型。将载荷加载到子模型的上下平面,如图5中箭头所示。为了提高计算速度和运算收敛性,选用理想的正弦非对称周期载荷,载荷函数选为F=200sin(20πt) MPa。
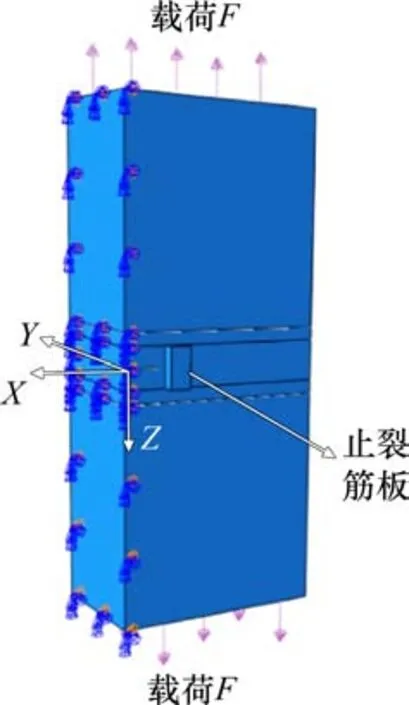
图5 带筋板裂纹扩展模型Fig.5 Crack propagation model of stiffened plate
2.2 裂纹开裂仿真
图6所示为带筋板子模型裂纹开裂过程的模拟结果,从中可知,裂纹接触到筋板以后,首先在筋板下侧开裂,随着载荷的持续作用,裂纹持续扩展,在筋板上也出现了裂纹,最后筋板完全开裂成两部分。

图6 带筋板子模型开裂应力图Fig.6 Cracking stress diagram of the stiffened plate model
为度量筋板的止裂效果,定义止裂系数为相同裂纹长度或深度时,止裂措施前后的载荷循环次数差与未采取止裂措施的裂纹循环次数的比值,用Nη表示。

式中:NS为采取止裂措施以后的裂纹循环次数;N为未采取任何止裂措施的裂纹循环次数。为了分析裂纹在长度和深度2个方向的扩展速率,定义Nηc和Nηa分别为长度止裂系数和深度止裂系数。
3 筋板参数对止裂效果的影响分析
通过改变筋板的关键参数,分析止裂板的位置、厚度、高度及宽度等参数对止裂效果的影响,研究不同参数筋板的止裂效果,并对其止裂效果进行评估。由于刀盘面板结构复杂,能够焊接筋板的位置有限,所以筋板尺寸不宜过大,经过预先实验分析,筋板参数的选择如表2所示。以位置参数研究为例,设置4组对照试验,其中3组筋板位置L取值分别为5,15和25 mm,筋板厚度t为4 mm,筋板高度h为8 mm,筋板宽度W为6 mm。第4组为不加筋板的空白对照组。分析其他参数时,参数设置按照表2依次取值。
3.1 筋板位置参数分析
研究筋板位置L对裂纹寿命的影响。设置4组对照试验,根据表2设置参数,即其中3组L取值分别为5,15和25 mm,t均为4 mm,h均为8 mm,W均为6 mm,第4组为不加筋板的空白对照组。

表2 筋板参数Table 2 Parameters of crack-stopping stiffened plate
在Abaqus中提取裂纹长度与对应的循环次数,通过Matlab进行平滑处理后得到图7。
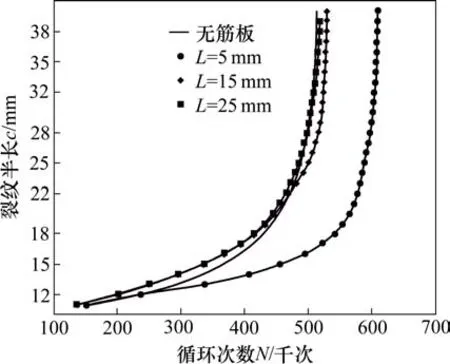
图7 不同位置参数的裂纹长度与循环次数关系Fig.7 Relationship between crack length and cycle number of different location parameters
从图7可知,对于L=5 mm组,在裂纹半长为12~18 mm时,即L=5 mm组筋板焊接位置处,裂纹扩展所需循环次数相比其他3组明显加大。裂纹半长大于18 mm以后扩展所需循环数与其他3组大致相同。
对于L=15 mm时,在裂纹半长小于22 mm时,曲线与L=25组完全重合。在裂纹半长为22~28 mm时,即L=15 mm组筋板焊接位置处,裂纹扩展所需循环次数对比L=25 mm组加大。裂纹半长大于28 mm时扩展所需循环次数与其他3组大致相同。
对于L=25 mm组,全程与对照组曲线变化趋势相近,在裂纹半长为32~38 mm时,即L=25 mm组筋板焊接位置,裂纹扩展所需循环次数稍微小于其他3组。
计算结果显示裂纹前期扩展所需循环次数较中后期更多。为更进一步分析裂纹扩展各个阶段的载荷循环次数,以不加筋板的对照组为例,选取裂纹半长为标准,将裂纹扩展分为3个阶段,得到各个阶段的循环次数占比如表3所示。由表3可知,裂纹半长从10 mm扩展到20 mm所需循环数占到整体循环次数的88.45%,裂纹扩展后期所需循环数仅占到2%,其原因是随着裂纹长度和深度的增加,裂纹前缘的应力集中效应越来越大,应力强度因子越来越大,裂纹扩展速率也随之增加。因此,裂纹前期的扩展速率将决定裂纹的最终寿命,分析裂纹前期的扩展速率更加有意义。
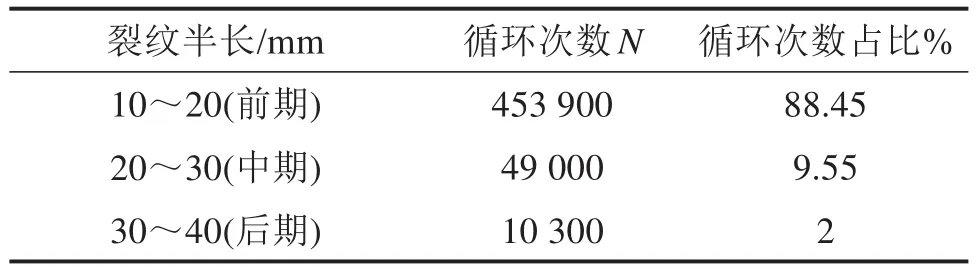
表3 对照组各阶段裂纹扩展所需循环数及比例Table 3 Cycle number and ratio of crack growth in each stage of control group
为了更好地分析裂纹扩展速率,以裂纹半长为横坐标,裂纹扩展速率的对数值为纵坐标得到图8。

图8 不同位置参数的裂纹长度方向扩展速率Fig.8 Propagation rate in the direction of crack length of different location parameters
从图8可知,对于L=5 mm组,当裂纹半长为12~18 mm时,其扩展速率低于其他3组,当大于18 mm时扩展速率高于对照组。由于前期扩展速率较小,所以整体止裂效果较好。
对于L=15 mm组,在22~28 mm时扩展速率有较明显放缓,且低于对照组。28 mm以后扩展速率逐渐变大,与L=5 mm组曲线重合并略高于对照组。由于筋板安装在裂纹扩展中期位置,虽然在筋板区域扩展速率较小,但是中期对整体寿命影响不大,所以止裂效果一般。
对于L=25 mm组,当裂纹半长小于18 mm时扩展速率与L=15 mm组相同,在18~28 mm时一直略低于对照组,在32~38 mm时扩展速率有较明显放缓。由于筋板安装在裂纹扩展后期位置,对整体寿命影响较小。所以即使在筋板区域裂纹扩展速率减小,止裂效果仍较差。
综上,加筋板区域的裂纹扩展速率明显放缓且小于对照组,因此筋板可有效降低裂纹长度方向的扩展速率。
图9为裂纹深度与循环次数的关系,从中可以看出裂纹L=15 mm和25 mm时2组的曲线与对照组大致重合,到最后发生较小偏离。L=5 mm组在裂纹深度为5~10 mm时与对照组完全重合,之后逐渐偏离,且偏离程度逐渐增大。

图9 不同位置参数的裂纹深度与循环次数关系Fig.9 Relationship between crack depth and cycle number of different location parameters
因此,裂纹附近加筋板不仅能够有效减缓裂纹长度方向的扩展,同时也能有效延缓深度方向的扩展。
从表3中可以看出,裂纹在扩展后期进入快速扩展阶段,循环次数变化很小,所以可以在裂纹扩展后期取一组裂纹尺寸作为裂纹失效尺寸,其对应的循环次数作为裂纹扩展寿命,用来计算止裂系数Nη。在长度方向取c=40 mm,深度方向取a=29 mm作为失效标准来计算各组的止裂系数。表4为根据式(5)计算的不同筋板位置的止裂系数,由表4中可知,同一组在长度和深度方向上止裂效果相差不大。筋板距离裂纹尖端越近,止裂效果越好。L=5 mm组止裂效果较好,裂纹寿命提高了18%左右。

表4 不同筋板安装位置的止裂系数Table 4 Crack stopping coefficients of different installation position of stiffened plate
3.2 筋板厚度参数分析
研究筋板厚度t对止裂效果的影响。同样根据表2设置4组实验,得到裂纹半长与循环次数的关系如图10所示。

图10 不同厚度参数的裂纹长度与循环次数关系Fig.10 Relationship between crack length and cycle number of different thickness parameters
从图10可知,加筋板的3组均有较好的止裂效果,其中t=2 mm组相比其他2组止裂效果稍差,t=4 mm组曲线与t=6 mm组相近。
图11为裂纹深度与循环次数的关系,从图中可知3组均有不错的止裂效果。其中t=4 mm组与t=6 mm组在图中曲线重合度均较高,t=2 mm组止裂效果相比其他2组稍差。

图11 不同厚度参数的裂纹深度与循环次数关系Fig.11 Relationship between crack depth and cycle number of different thickness parameters
综上可知,筋板厚度对筋板的止裂效果存在一定的影响,筋板越厚,裂纹在长度和深度方向上扩展速率都越慢,止裂效果越明显。从表5中可知t=4 mm组与t=6 mm组止裂系数均在19%左右,说明筋板增加到一定厚度值,其对止裂效果的影响将不再显著。
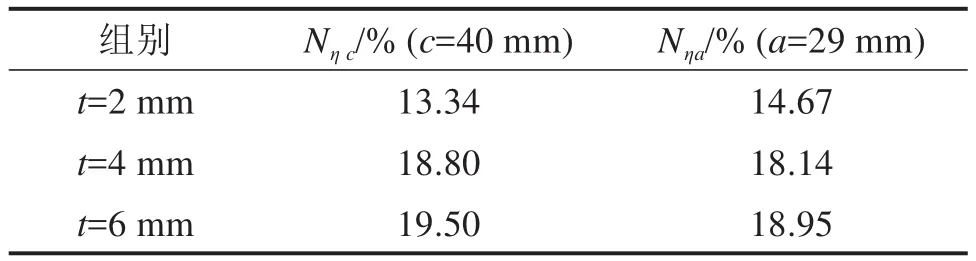
表5 不同筋板厚度的止裂系数Table 5 Crack stopping coefficients of different thickness of stiffened plate
3.3 筋板高度参数分析
研究筋板高度h对止裂效果的影响。同样根据表2设置4组实验,得到裂纹长度与循环次数关系如图12所示,裂纹长度方向扩展速率如图13所示。
从图12中可知,h=12 mm组止裂效果最好,h=8 mm组止裂效果较好,h=4 mm组曲线大部分和对照组曲线重合,几乎没有止裂效果。结合图13可知,3组在裂纹半长为12~18 mm时,即筋板焊接位置处,扩展速率均低于对照组,且筋板高度值越大,扩展速率越低。在18 mm以后扩展速率均高于对照组且有一小峰值,之后逐渐与对照组曲线重合。出现峰值是因为裂纹在贯穿筋板之后会在子模型内部率先扩展,此时表面还未开裂,所以会导致表面应力集中,扩展加速。
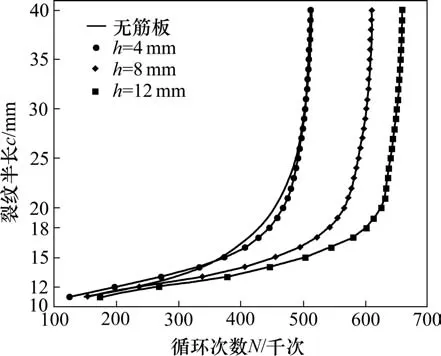
图12 不同高度参数的裂纹长度与循环次数关系Fig.12 Relationship between crack length and cycle number of different height parameters
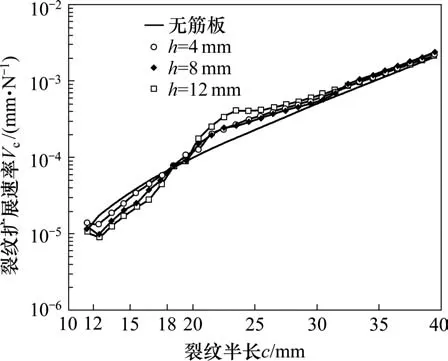
图13 不同高度参数的裂纹长度方向扩展速率Fig.13 Propagation rate in the direction of crack length of different height parameters
从图14中可知,h=12 mm组止裂效果最好,h=8 mm止裂效果较好,h=4 mm止裂效果较差。
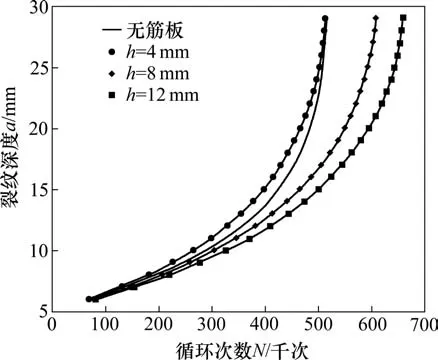
图14 不同高度参数的裂纹深度与循环次数关系Fig.14 Relationship between crack depth and cycle number of different height parameters
从表6中可知,随着筋板高度的增加,止裂系数明显增大,h=12 mm组止裂效果最好,裂纹寿命提高了28%左右。

表6 不同筋板高度的止裂系数Table 6 Crack stopping coefficients of different height of stiffened plate
综上,筋板高度对裂纹寿命影响较大。当h=4 mm时,由于筋板高度过小,不能很好改善裂纹尖端的应力分布,所以几乎没有止裂效果。随着筋板高度的增加,对裂纹尖端的应力集中有所改善,止裂效果有较明显提升。
3.4 筋板宽度参数分析
研究筋板宽度W对止裂效果的影响。为减少筋板位置L对筋板宽度止裂性能的影响,L取15 mm。同样根据表2设置4组对照试验,得到裂纹长度与循环次数关系如图15所示,裂纹深度与循环次数关系如图16所示。
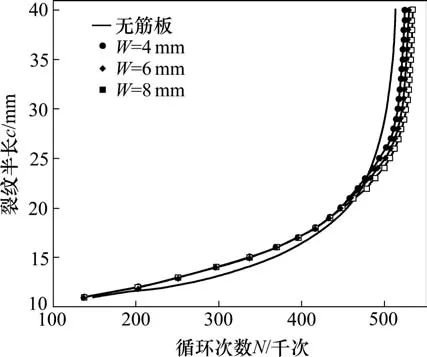
图15 不同宽度参数的裂纹长度与循环次数关系Fig.15 Relationship between crack length and cycle number of different width parameters
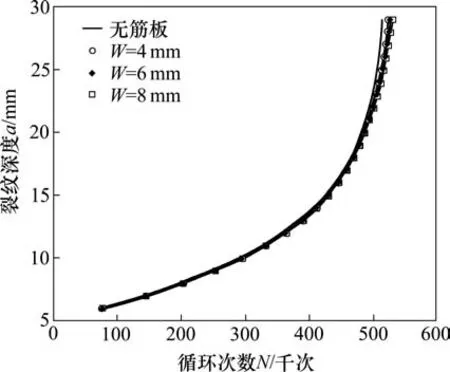
图16 不同宽度参数的裂纹深度与循环次数关系Fig.16 Relationship between crack depth and cycle number of different width parameters
从图15中可知,3条曲线前期重合,当裂纹扩展到焊接筋板位置时,3条曲线在各自筋板焊接位置发生偏离。
从图16中可知,3条曲线前期重合且与对照组曲线重合,裂纹深度扩展至20 mm以后3条曲线逐渐偏离对照组,但是偏离量均较小。
从表7中可知,3组止裂系数均在1%~4%之间,随着筋板宽度的增加,止裂系数也随之增加,但是增长幅度较小。综上,筋板宽度值对延缓裂纹扩展有一定效果,但效果并不明显,且止裂效果与筋板宽度成正相关。

表7 不同筋板宽度的止裂系数Table 7 Crack stopping coefficients of different width of stiffened plate
4 结论
1) 长度方向的止裂系数Nηc和深度方向的止裂系数Nηa相差很小,即止裂效果在长度和深度方向具有一致性。
2) 裂纹扩展初始阶段,扩展速率较慢,需要的载荷循环次数较多,裂纹扩展中后期,扩展速率加快。裂纹半长从10 mm扩展到20 mm所需循环数占到整体循环次数的88.45%,裂纹扩展后期所需循环数仅占2%。裂纹止裂的关键是尽早发现裂纹,及时止裂。
3) 止裂筋板的位置参数L对止裂效果影响较大,筋板距离裂纹尖端越近,止裂效果越好,且变化幅度明显,L=5 mm时相比对照组裂纹寿命提高了18%左右。筋板厚度参数t对止裂效果也有一定影响,但随着t的不同取值,各实验组的止裂系数变化幅度较小,而总的趋势是筋板厚度越大,止裂效果越好,t=6 mm时相比对照组裂纹寿命提高了19%左右。筋板高度参数h对止裂效果影响最大,筋板高度越高,止裂效果越好,且提高幅度最为明显,h=12 mm时相比对照组裂纹寿命提高了28%左右。筋板宽度参数W对止裂效果影响最小,W的不同取值只能将裂纹寿命提高3%左右。
4) 对于止裂板设计和安装的经济性而言,需要重点关注筋板安装位置和筋板高度参数,缩短其安装距离并提高筋板高度。同时,不应过度追求筋板厚度参数和筋板宽度参数的优化,以保证在规定成本下止裂效果的最大化,从而提高止裂筋板的经济性。

