TBM的平面刀盘与两级刀盘的力学性能对比分析

耿麒,魏正英,孟昊,卓兴建,贾连辉,贺飞,楚华丽

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.中铁工程装备集团有限公司,450016,郑州)



TBM的平面刀盘与两级刀盘的力学性能对比分析

耿麒1,魏正英1,孟昊1,卓兴建2,贾连辉2,贺飞2,楚华丽1

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.中铁工程装备集团有限公司,450016,郑州)

为解决全断面岩石掘进机(TBM)大直径(>10 m)平面刀盘承受的破岩载荷、偏心载荷过大会造成刀盘大变形、主轴承损坏的问题,引入一种两级刀盘。基于应用在西秦岭隧道的平面刀盘,采用灰关联分析的方法设计了两级刀盘的结构;建立复合岩层条件下平面刀盘和两级刀盘的受力分析模型,对比分析了两种刀盘的破岩总推力和扭矩、刀盘径向不平衡力和倾覆力矩;建立均一岩层条件下两种刀盘的有限元模型,对比分析了两种刀盘的变形和应力分布。结果表明,两级刀盘的各级破岩总推力、扭矩、径向不平衡力、倾覆力矩、刀盘变形和最大应力均比平面刀盘小,说明两级刀盘有效地把破岩载荷分散到各级刀盘,同时提高了刀盘刚度,避免了刀盘应力过度集中,有效减小了刀盘的偏心载荷。

全断面岩石掘进机;两级刀盘;平面刀盘;复合岩层

掘进机(TBM)是一种用于隧道全断面开挖的大型专用工程机械,被广泛应用于水电、铁路、地铁隧道工程。刀盘是TBM掘进的关键部件,直接承受着来自液压推进缸的总破岩载荷;刀盘主轴承是支撑刀盘掘进动作的关键部件,不仅承受着刀盘轴向破岩总载荷,还承受着刀盘的径向不平衡力和倾覆力矩[1]。对于大直径长距离岩石隧道,由于开挖断面大使得刀盘承受的破岩总载荷过大而造成刀盘面大变形;由于隧道过长使得掌子面岩层复杂多变、刀盘受力不平衡,进而造成主轴承的偏心载荷过大。

针对上述问题,国内外的研究主要集中在刀盘的结构设计与优化方面,具体包括刀盘几何结构设计、滚刀布局优化设计、刀盘结构主参数优化设计。刀盘几何结构设计方面,锥面刀盘和球面刀盘的刀盘面变形小于通用的平面式刀盘,但由于倾斜安装的滚刀数目增多,使得刀盘径向不平衡力增大[2-3];滚刀布局优化设计方面,霍军周等针对均一掌子面研究了滚刀布局模式与刀盘受力特性的关系,提出了基于遗传算法、蚁群算法、协同进化算法、灰关联分析等理论的滚刀布局优化方法[4-6],使得刀盘的变形、径向不平衡力、倾覆力矩都有不同程度的减小;刀盘结构主参数优化设计方面,李震等基于遗传算法进行了刀盘面板厚度等12个刀盘结构主参数的优化设计[7],使得刀盘面的应力有所减小,但是刀盘面的变形并未明显改善。对于均一掌子面岩层,上述研究可使刀盘力学性能得以改善,但是对于由不同岩石组成的复合掌子面岩层,上述研究则无法改善刀盘的力学性能。

本研究引入了一种两级刀盘,首先基于应用在西秦岭隧道的开挖直径为10.23 m的罗宾斯平面刀盘,采用灰关联分析的方法[8-9]设计了两级刀盘的结构,然后建立了复合岩层条件下平面刀盘和两级刀盘的受力分析模型,对两种刀盘的力学性能进行了对比分析,结果表明:两级刀盘的刀盘破岩总推力、总扭矩、刀盘径向不平衡力和倾覆力矩、刀盘变形量和最大应力均明显小于平面刀盘。

1 两级刀盘结构设计

1.1 两级刀盘基本结构

两级刀盘的基本结构如图1所示[10]。一级刀盘为小直径平面刀盘,同轴安装在环柱形的二级刀盘内。两级刀盘轴向相对固定且刀盘面交错,具有各自独立的驱动系统,共用一套推进系统和皮带出碴系统,二级刀盘的岩碴通过开设在刀盘支撑环上的出碴口流入一级刀盘腔内,由皮带出碴机运走。

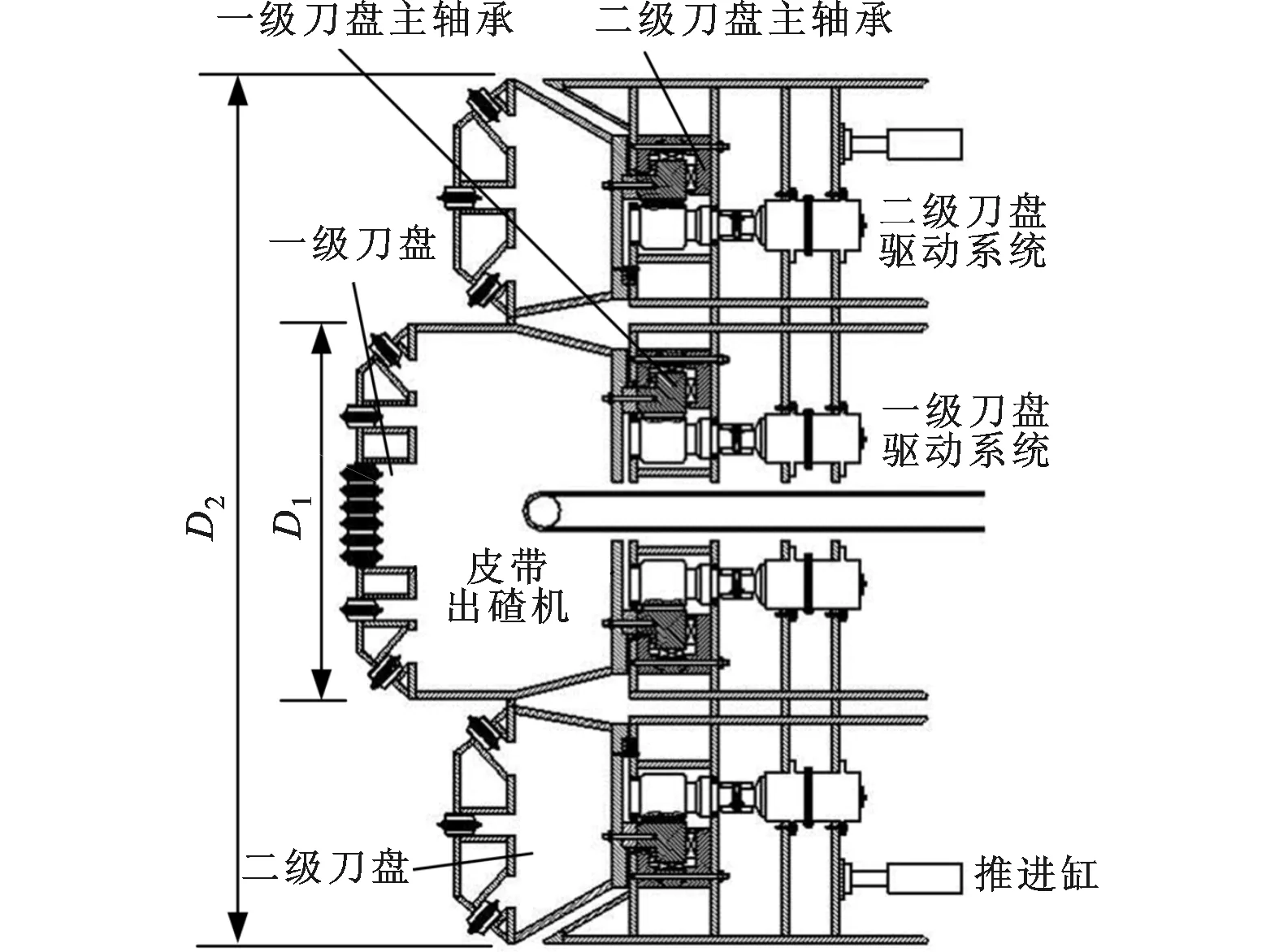
图1 两级刀盘基本结构示意图

1.2 两级刀盘滚刀布局设计

西秦岭隧道的TBM刀盘如图2所示,其滚刀为直径483 mm的罗宾斯滚刀,正滚刀平均刀间距为76 mm,由施工统计,隧道线上78.5%的岩石类型为III级千枚岩,平均单轴抗压强度(UCS)为80 MPa,巴西抗拉强度(BTS)为6 MPa。以此为基础进行了两级刀盘的滚刀布局设计,即滚刀极径r、极角θ和倾角γ设计(见图3),分为边滚刀的倾角和刀间距设计、滚刀的极径设计、滚刀的极角设计,步骤如下。

图2 西秦岭隧道TBM刀盘

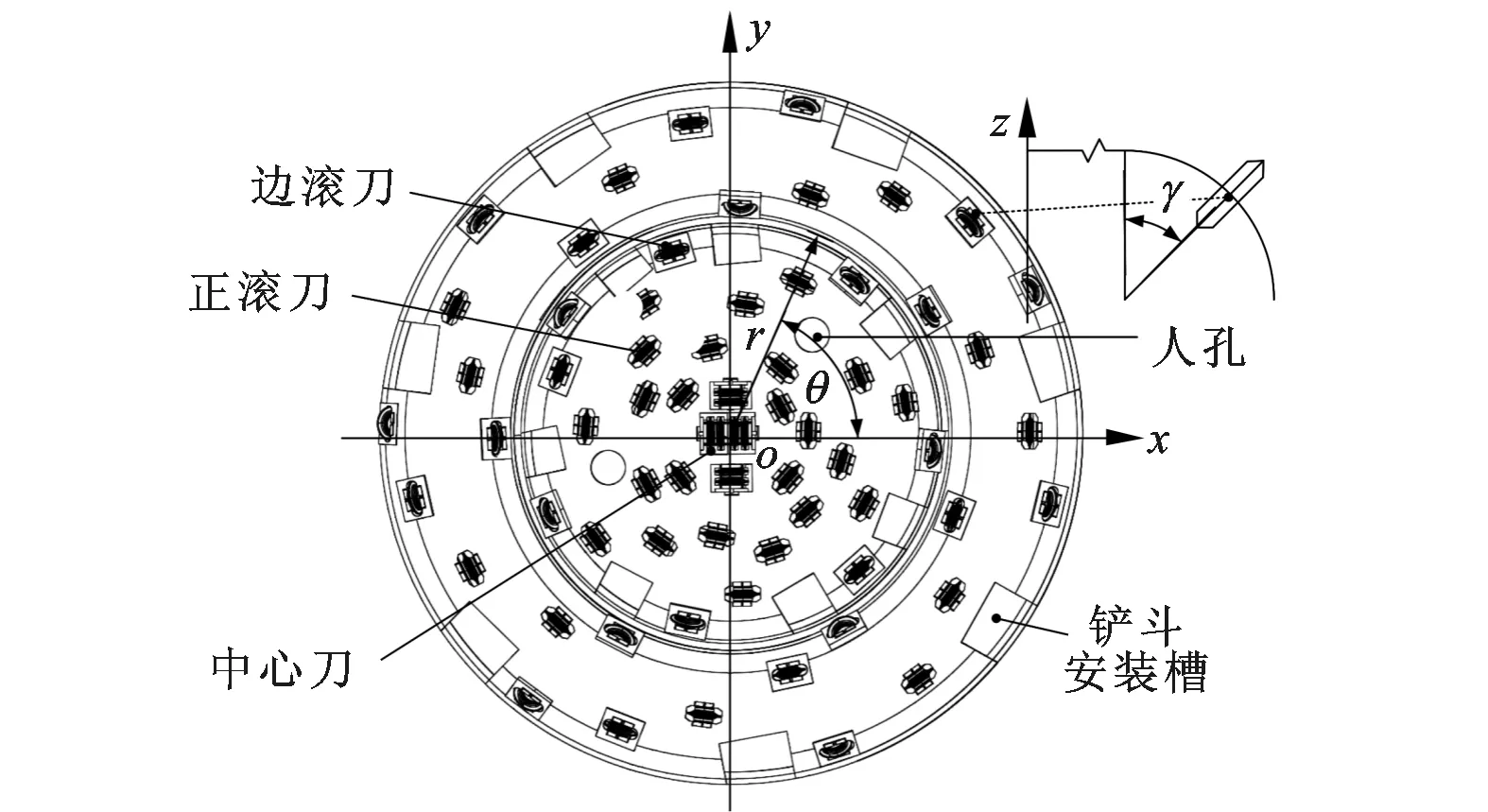
图3 两级刀盘盘面基本布置要素

(1)边滚刀的倾角和刀间距设计。数学模型为

(1)

式中:Xγ为一个边滚刀群的倾角、刀间距方案;Rt为刀盘过渡区域半径;h为刀高;γ1、S1分别为第一把边滚刀的倾角和刀间距;γn、Sn分别为第n把边滚刀的倾角和刀间距;Δγ为边滚刀倾角的公差;n为设计区域的边滚刀数目。

约束条件:边滚刀刀间距小于正滚刀刀间距;边滚刀刀间距随刀号增大而减小;最外一把边滚刀倾角大于55°;最外一把边滚刀刀间距为20～25 mm[11]。

(2)滚刀的极径设计。数学模型为

(2)

式中:Xr为一个滚刀群的极径方案;r1p为一级刀盘滚刀极径;p为一级刀盘滚刀数目;r2q为二级刀盘滚刀极径;q为二级刀盘滚刀数目。

评价指标:f1为两级刀盘破岩推力差;f2为两级刀盘破岩扭矩差。

约束条件:刀孔之间无干涉;刀孔与人孔间无干涉;刀孔与铲斗安装槽间无干涉。

(3)滚刀的极角设计。数学模型为

(3)

式中:Xθ i为分组i的滚刀极角方案;θi t为分组i中第t把滚刀的极角。

评价指标:g11、g21为一、二级刀盘径向不平衡力;g12、g22为一、二级刀盘倾覆力矩;g13、g23为一、二级刀盘滚刀群质心偏斜量。

约束条件:刀孔间无干涉;刀孔与人孔间无干涉;刀孔与铲斗安装槽间无干涉。

以上数学模型采用灰关联分析的方法[6]进行求解。模型中的滚刀破岩法向力FN和滚动力FR采用科罗拉多矿业学院载荷预测模型[2]进行计算,由文献[2],滚刀破岩侧向力Fs比FN、FR小得多,且尚无广泛认可的预测理论,故在计算中可忽略。各评价指标计算如下,最后得到两级刀盘的参数设计结果如表1所示。

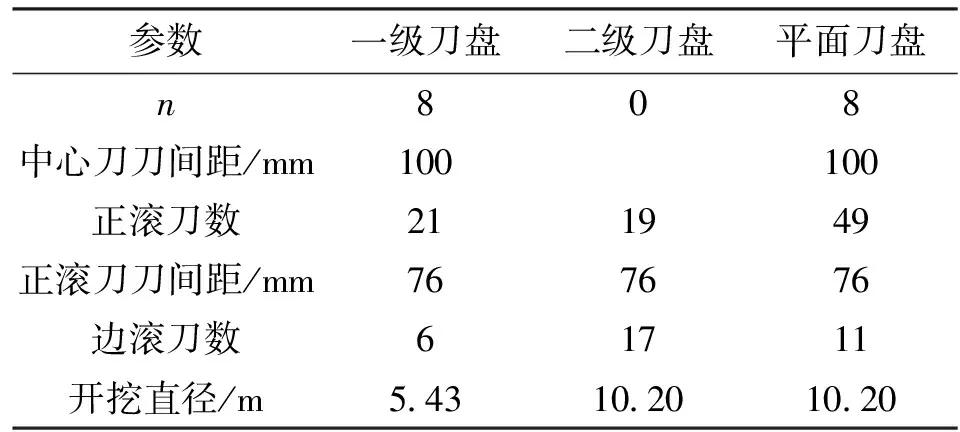
表1 两级刀盘参数设计结果

两级刀盘破岩推力差

(4)

两级刀盘破岩扭矩差

(5)

刀盘径向不平衡力

(6)

对于中心刀和正滚刀

对于边滚刀

式中:FE为滚刀离心惯性力。

刀盘倾覆力矩

(7)

对于中心刀和正滚刀

对于边滚刀

式中:Mg为滚刀的科氏惯性矩,Mg=mcω2ρrc,mc为滚刀质量;rc为滚刀半径;ω为刀盘转速。

滚刀群质心偏斜量为滚刀的位置沿刀盘轴线方向被投影到刀盘正面(见图3)后,滚刀群质量的集中点(质心)与刀盘中心的偏斜距离,即

(8)

式中:x、y为滚刀在xOy平面上的直角位置坐标。

2 复合岩层下刀盘受力分析

2.1 计算模型

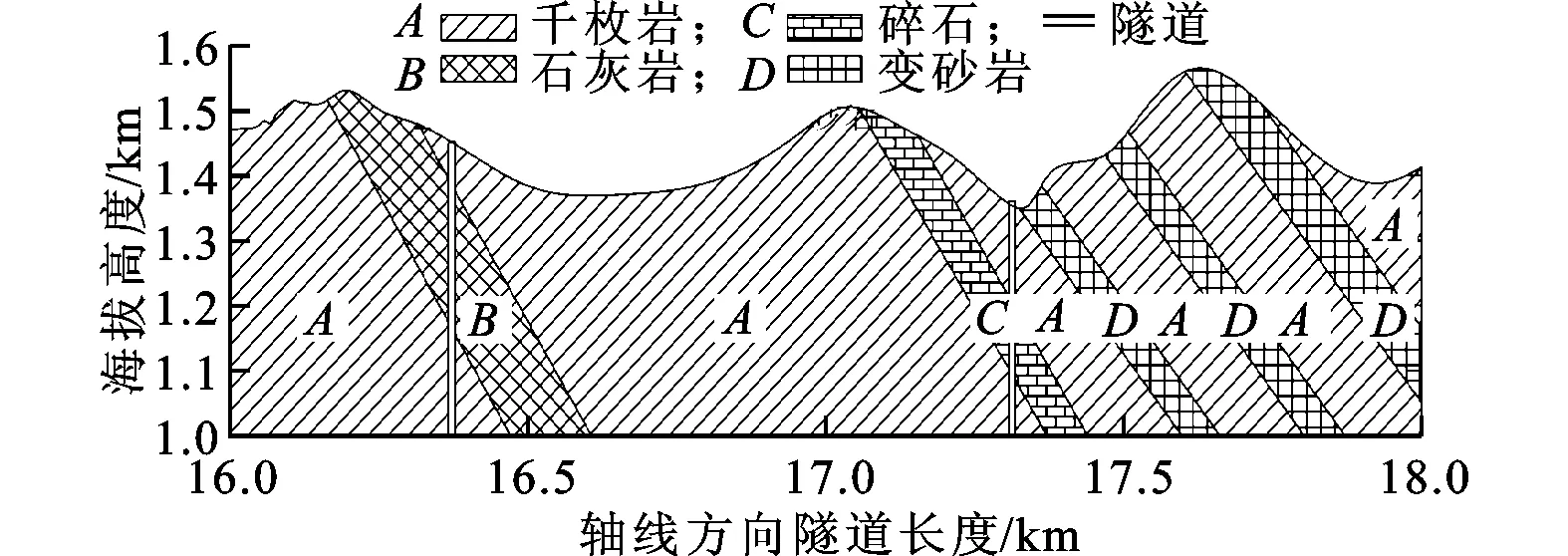
图4 西秦岭隧道某区段岩层剖面图

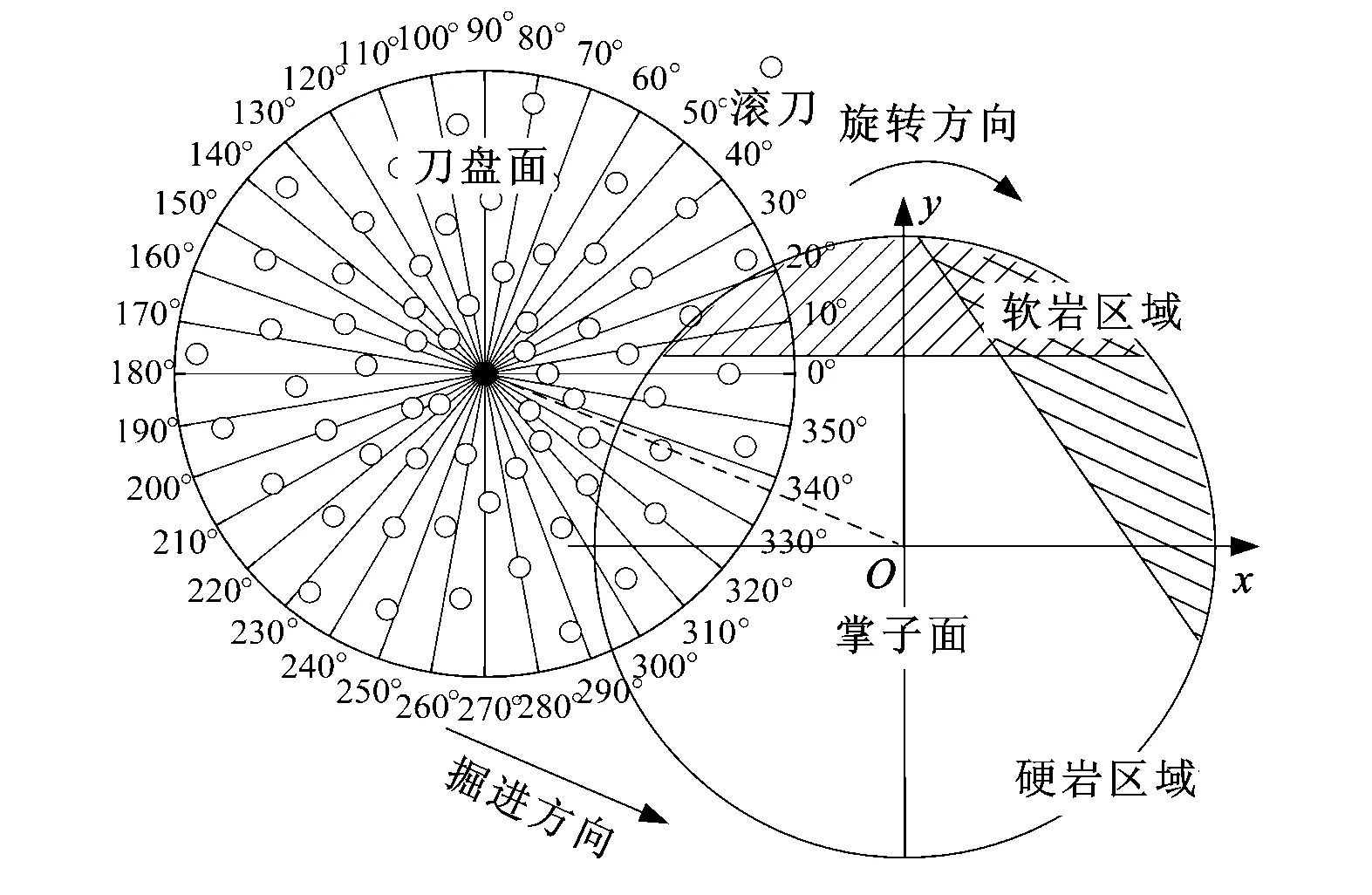
图5 平面刀盘复合岩层受力计算模型

如图4所示,当TBM穿越两种岩层的交界面时,掌子面由两种岩石构成。随着TBM掘进,两种岩石在掌子面上所占的面积比会发生变化,同时不同的交界面上两种岩石的强度比也会发生变化。如图5所示,针对平面刀盘,建立了考虑掌子面上软岩的面积比b、软硬岩UCS比a的刀盘受力分析模型。保持刀盘面固定,对掌子面施加力使其转速与刀盘实际转速大小相等、方向相反,这样刀盘旋转转化为掌子面的反向旋转,从而形成两种岩石交界线的旋转,由此可确定每把滚刀所切削的岩石类型。由于刀盘回转一周的掘进量(10 mm左右)远小于掌子面的直径(10 m左右),因此刀盘回转一周的a值基本不变,故将掌子面上两种岩石交界线绕掌子面中心每次旋转10°,直至一周,对36种交界线情况下刀盘的受力取平均值,可得到刀盘回转一周的受力。如图6所示,采用同样的方法,建立了两级刀盘的复合岩层受力计算模型。相对误差定义为

(9)

式中:Gh为交界线取硬岩时评价指标的计算值;Gs为交界线取软岩时评价指标的计算值。

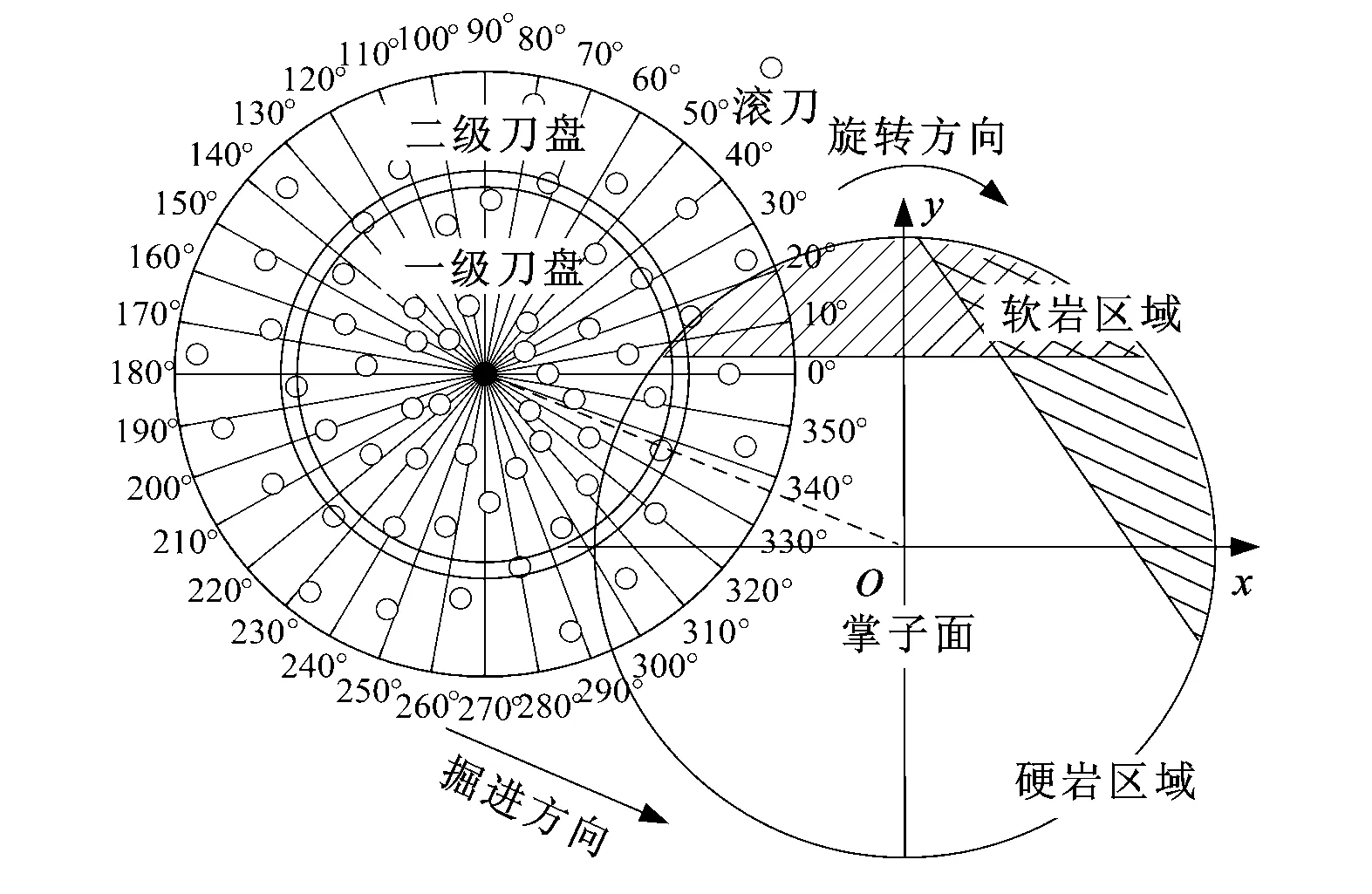
图6 两级刀盘复合岩层受力计算模型

如图7所示,以平面刀盘为例,对于刚好落在软、硬岩交界线上的滚刀,分别假设其切削软、硬岩,取a为0.1、b为0.5,计算刀盘力学性能的主要评价指标(总推力、总扭矩、径向不平衡力、倾覆力矩),发现其相对误差均小于3%,即交界线上的岩石类型对计算结果影响较小。本文2.2节中交界线上的滚刀载荷均按软岩计算。

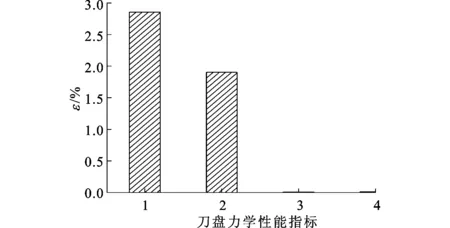
1:总推力;2:总扭矩;3:径向不平衡力;4:倾覆力短 图7 交界线上滚刀切削软、硬时刀盘力学指标的相对误差

2.2 计算结果及分析

假定掌子面上硬岩区域的UCS为150 MPa,软岩区域的UCS为150aMPa,a取值为0.1,0.2,…,1.0;滚刀切深取6 mm,岩石BTS取6 MPa,刀盘受力计算结果如图8～图15所示。

对于平面刀盘,由图8、图9知:对给定的a值,刀盘总破岩推力和扭矩随b值增大而减小,这是因为b值增大使得掌子面软岩区域增大;对给定的b值,刀盘总破岩推力和扭矩随a值增大而增大,这是因为a值增大使得掌子面上软岩单轴抗压强度增大。由图10、图11知:对给定的a值,刀盘径向不平衡力和倾覆力矩随b值增大呈先增大后减小的规律,在b=0.5即掌子面上软、硬岩各占一半时达到最大值;当b=0.1,0.2,…,0.9时,刀盘径向不平衡力和倾覆力矩随a值增大而减小,这是因为a值增大使得掌子面上两种岩石的强度差变小;当b=1时,掌子面为均一岩石,刀盘径向不平衡力和倾覆力矩随a值增大而增大,即随岩石单轴抗压强度增大而增大。

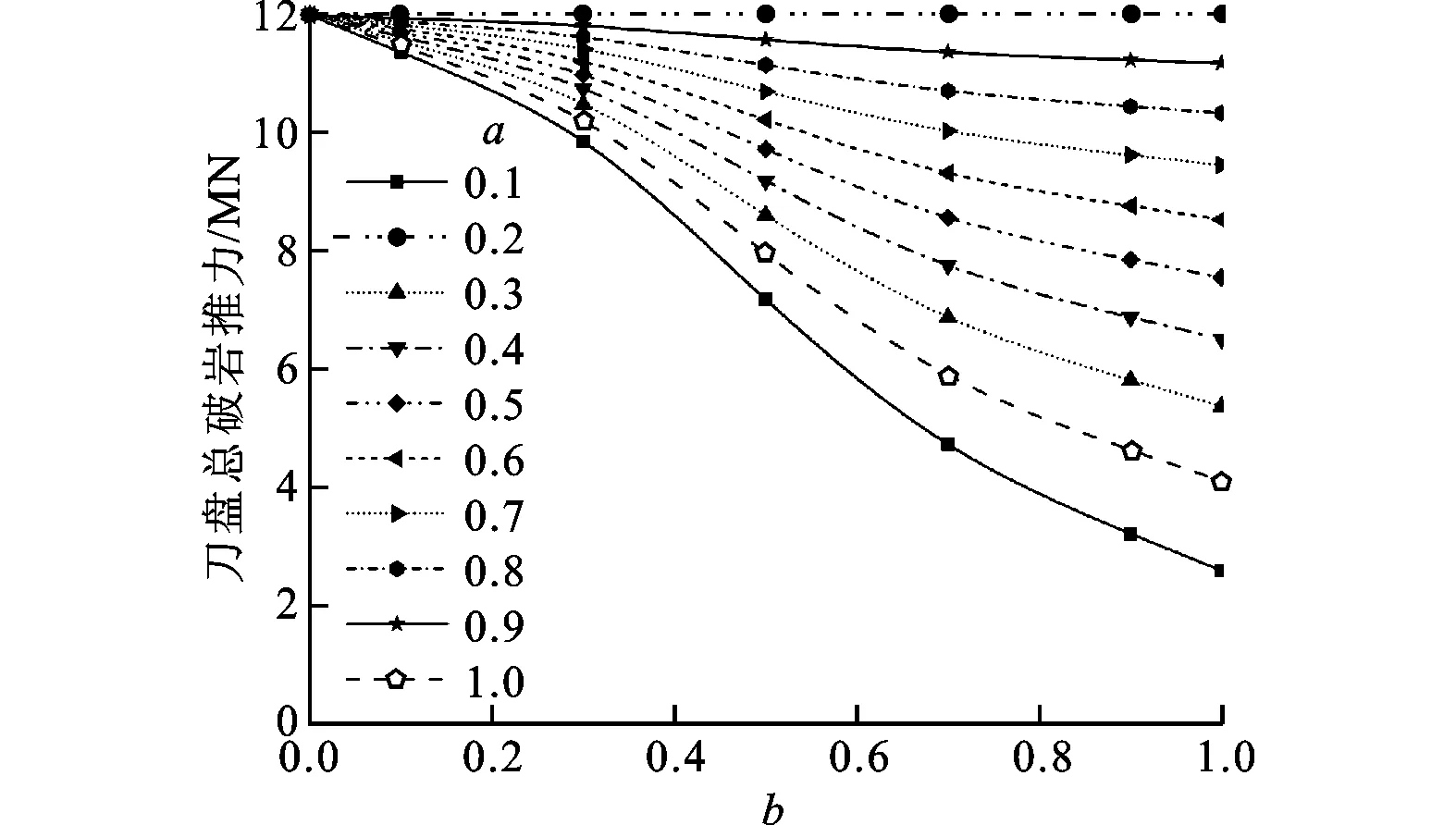
图8 平面刀盘开挖复合岩层刀盘总破岩推力

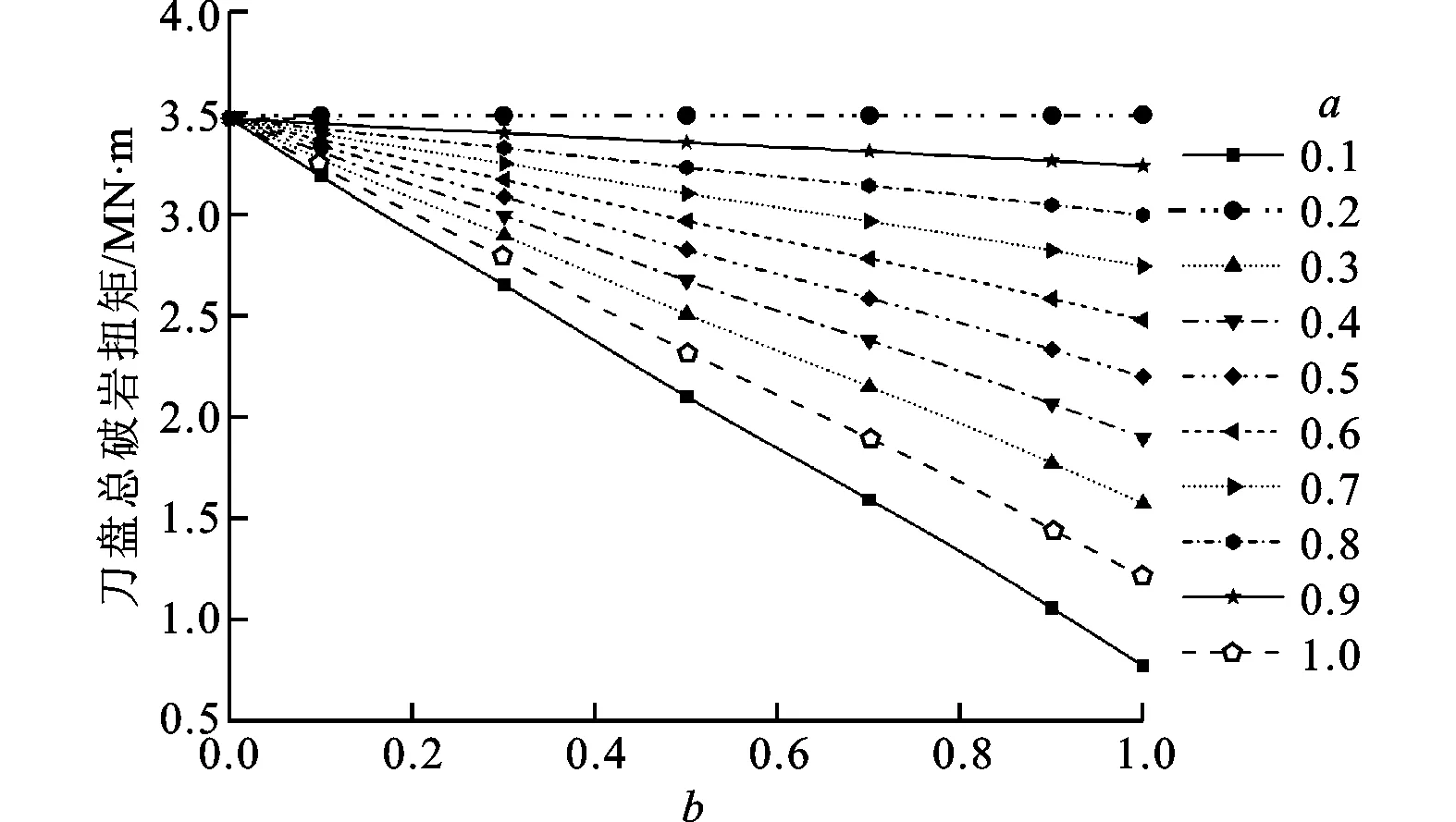
图9 平面刀盘开挖复合岩层刀盘总破岩扭矩

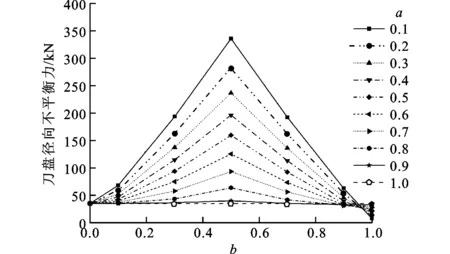
图10 平面刀盘开挖复合岩层刀盘径向不平衡力

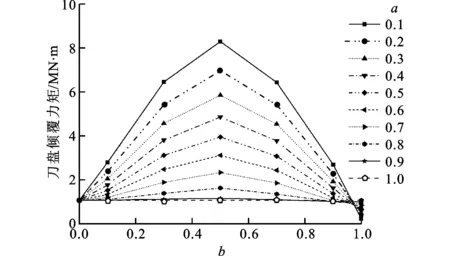
图11 平面刀盘开挖复合岩层刀盘倾覆力矩

图12 复合岩层下平面与两级刀盘总破岩推力对比

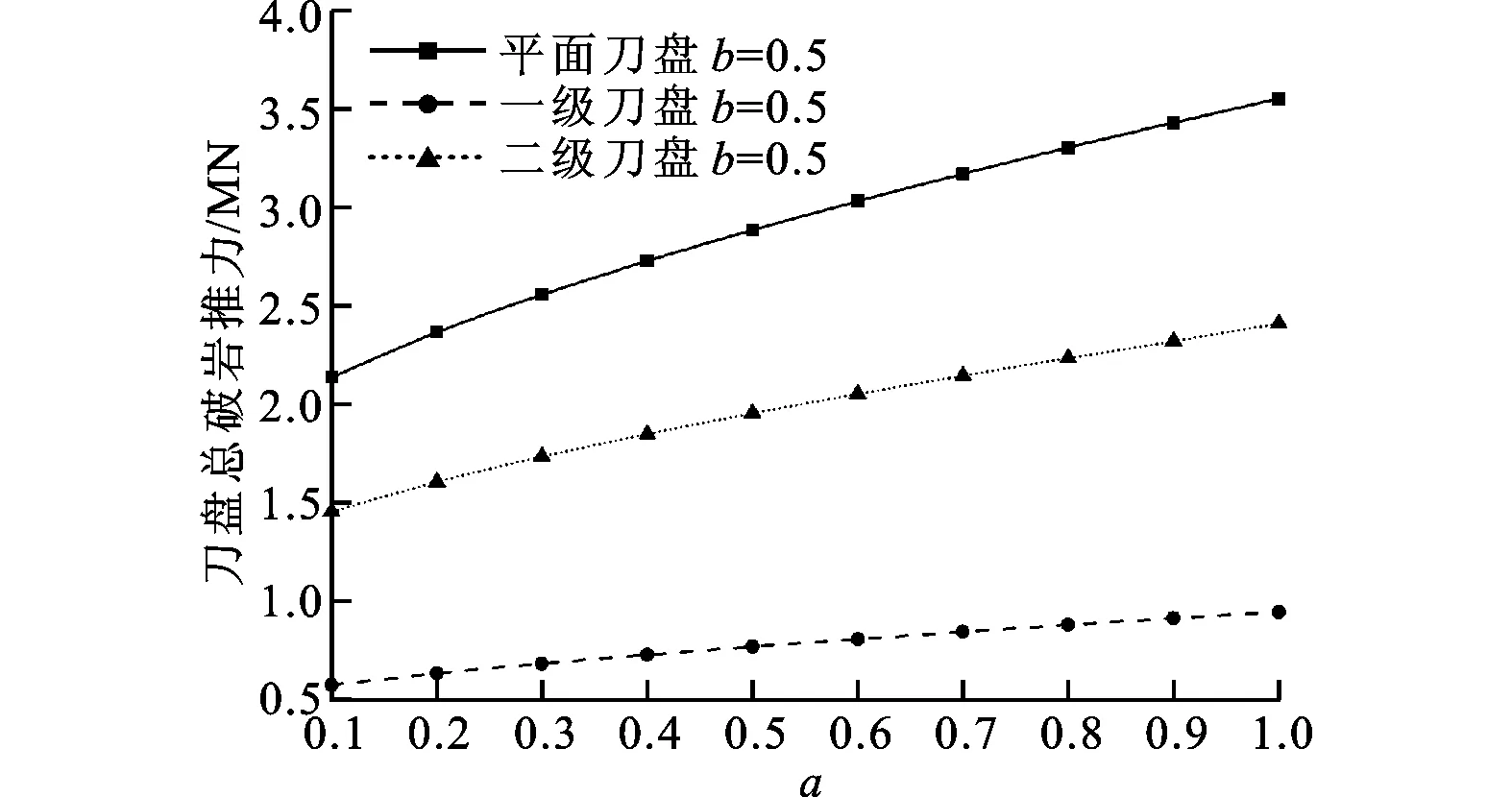
图13 复合岩层下平面与两级刀盘总破岩扭矩对比

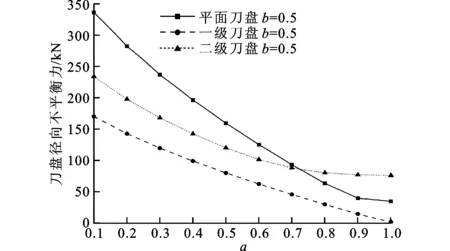
图14 复合岩层下平面与两级刀盘径向不平衡力对比

图15 复合岩层下平面与两级刀盘倾覆力矩对比

由图10、图11知,刀盘的径向不平衡力和倾覆力矩在b=0.5时最大,因此对比分析b=0.5时平面刀盘和两级刀盘的受力情况如下。由图12、图13知,两级刀盘各级的破岩总推力和扭矩均比平面刀盘小;由图14、图15知,除了a>0.8情况,两级刀盘各级的径向不平衡力和倾覆力矩均比平面刀盘小;表2为图12～图15中两种刀盘各力学指标的平均值,两级刀盘各级的指标平均值均比平面刀盘小。这说明在复合岩层条件下,两级刀盘结构不仅可以有效减小刀盘的破岩推力和扭矩,还可以有效减小各级刀盘的径向不平衡力和倾覆力矩,从而有效改善刀盘和主轴承的受力。

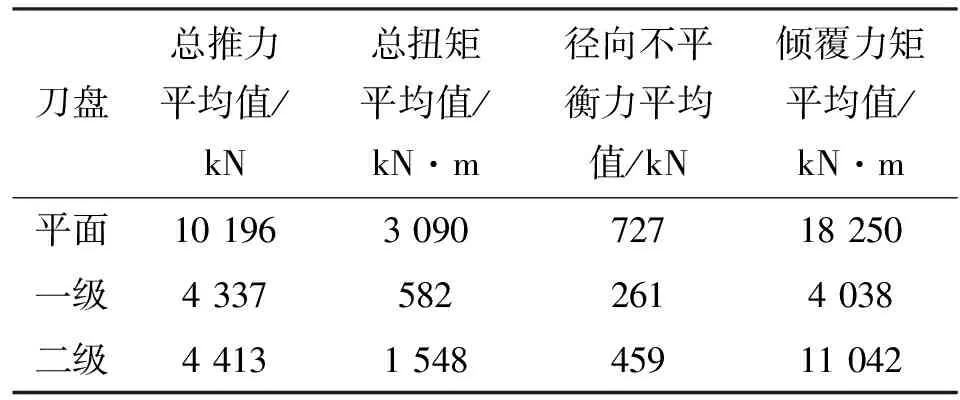
表2 刀盘力学性能指标统计平均值

3 平面刀盘与两级刀盘变形及应力分析

3.1 计算模型

平面刀盘和两级刀盘的几何尺寸如图16、图17所示。建立两种刀盘的有限元模型,划分四面体网格,平面刀盘单元数为27.1万,节点数为43.8万,两级刀盘单元数为41.9万,节点数为72.4万,刀盘材料为结构钢,密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.3。两种刀盘的工作条件为:掌子面岩石均一,UCS为150 MPa,BTS为6 MPa,切深为6 mm。滚刀的破岩载荷由CSM模型计算得到,施加在刀座上。

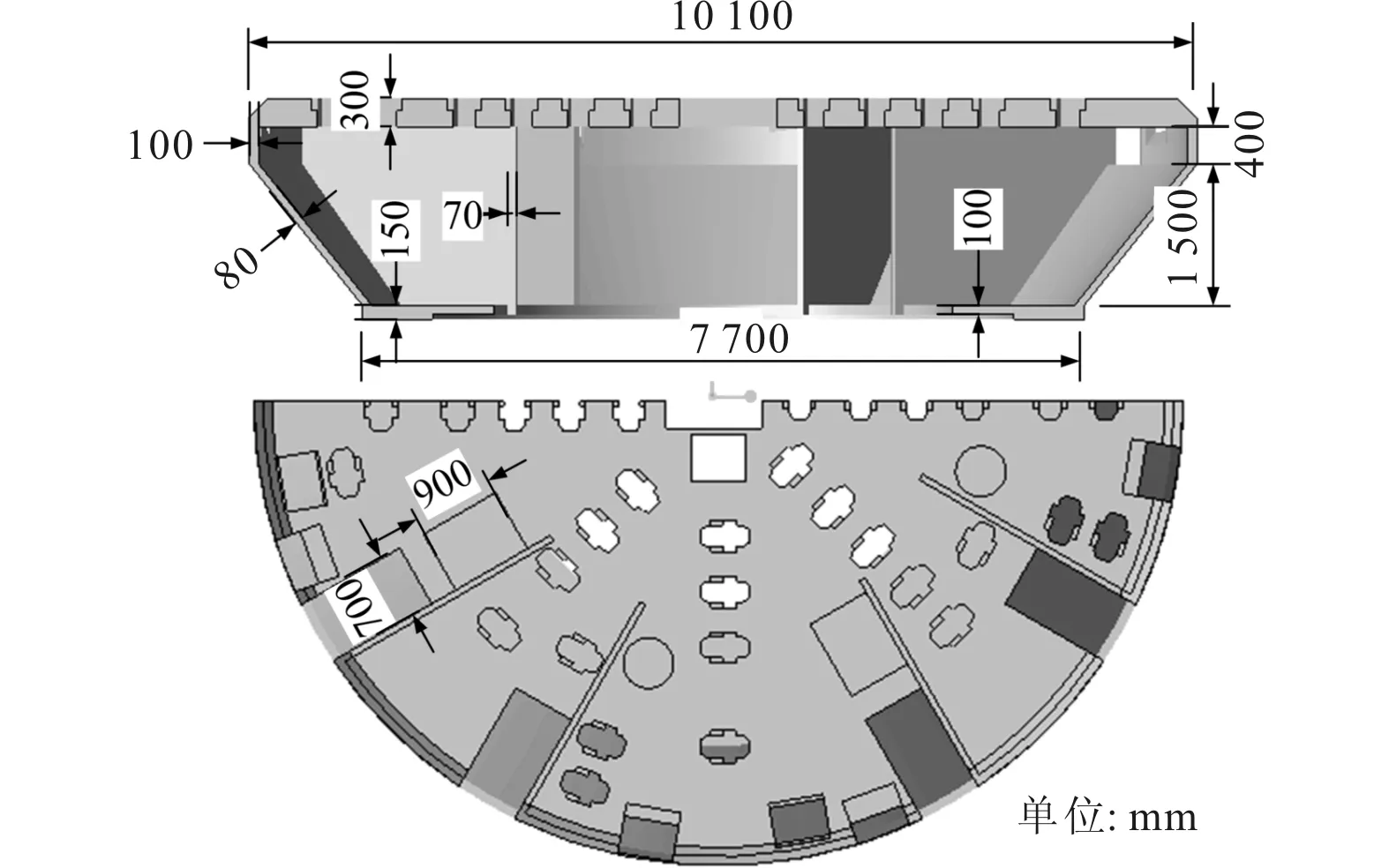
图16 平面刀盘结构及几何尺寸

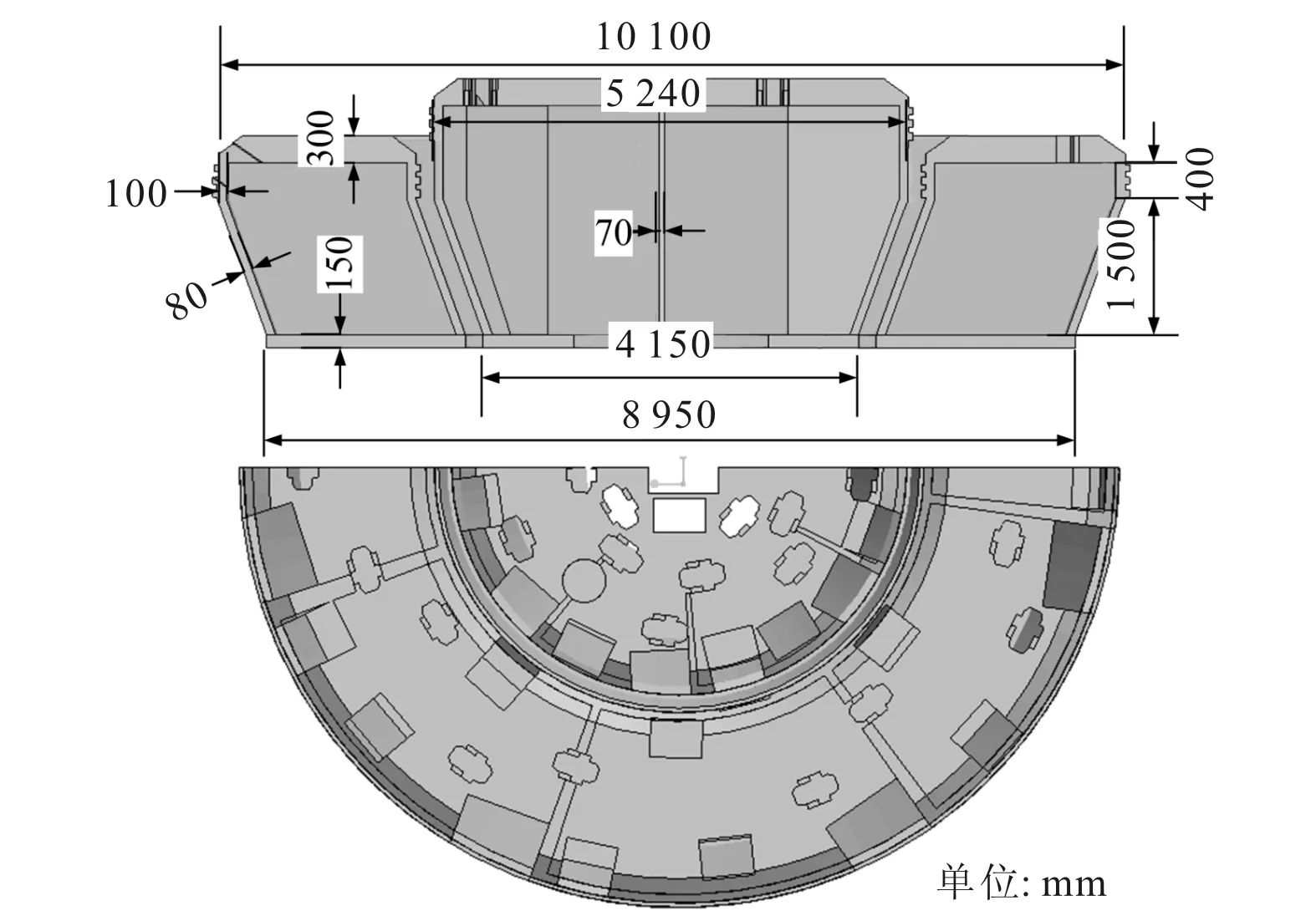
图17 两级刀盘结构及几何尺寸

3.2 计算结果及分析

刀盘所承受的最大载荷为沿刀盘轴向(z向)的法向破岩力,因此刀盘的最大变形也发生在z向。由图18、图19知:平面刀盘的最大z向变形量为1.55 mm,不满足工程上最大刀盘变形量小于1 mm的要求[12];两级刀盘的最大z向变形量为0.69 mm,两级刀盘的变形量比平面刀盘小,这是由于两级刀盘将载荷分散到各级上(见图12、图13),同时两级刀盘比平面刀盘多了两组支撑锥环,结构刚度比平面刀盘大。平面刀盘和两级刀盘盘面的z向变形量从刀盘中心到外周逐渐减小,且变形云图为同心圆状,因此将刀盘面上的单元节点按距刀盘中心距离递增的方向分为20组,统计每个分组内节点的z向变形量和距刀盘中心距离的平均值。由图20知:平面刀盘和两级刀盘的z向变形主要发生在刀盘半径小于3 000 mm的区域;两级刀盘的变形量比平面刀盘小,且沿刀盘半径方向变形量变化更为平缓。

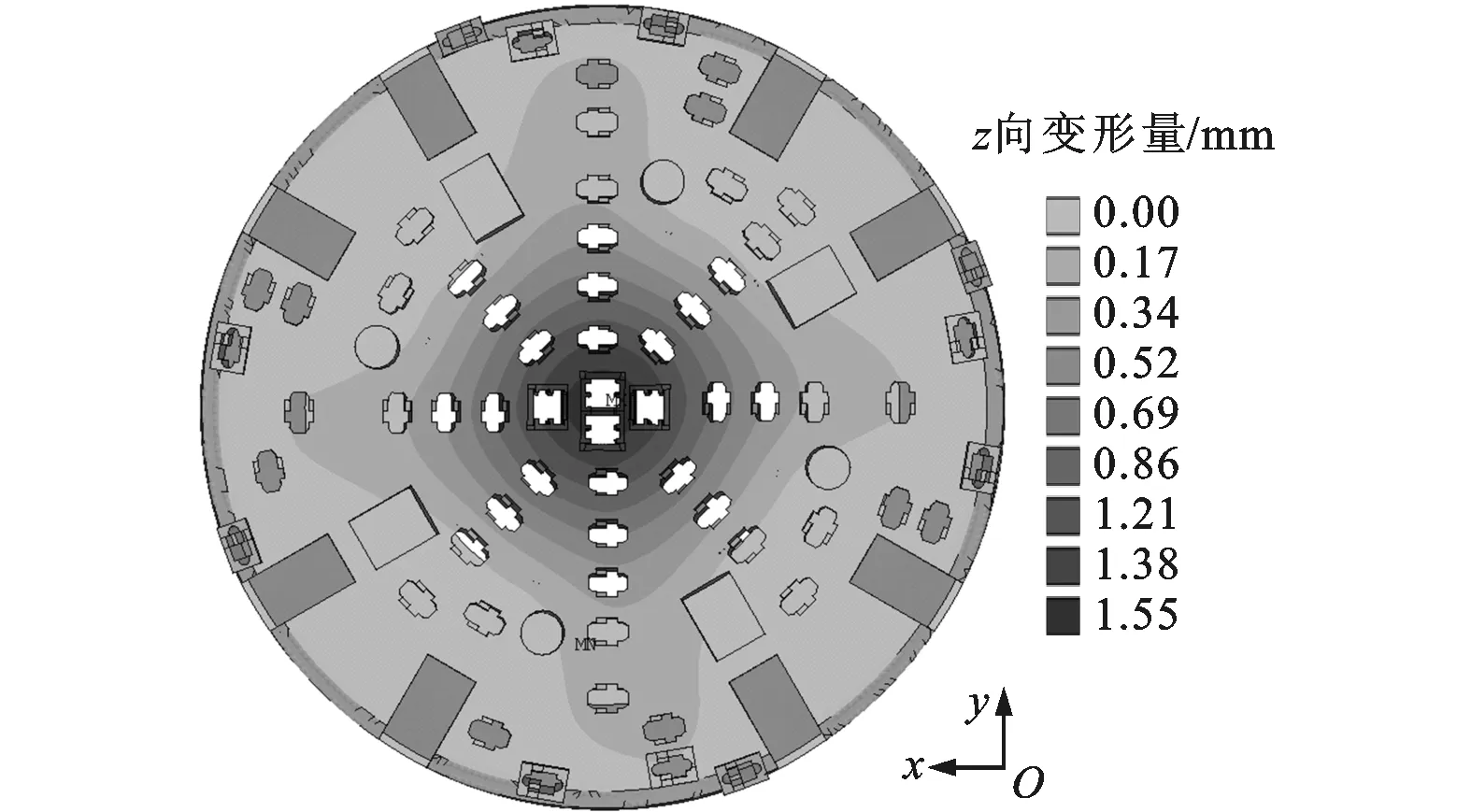
图18 平面刀盘z向变形分布云图

图19 两级刀盘z向变形分布云图

图20 刀盘面的z向变形在刀盘径向的统计平均值

由图21、图22知,平面刀盘的最大应力为213 MPa,两级刀盘的最大应力为98 MPa,两级刀盘的刀盘应力比平面刀盘小,这是由于两级刀盘的滚刀布局设计使得滚刀的分布更为均匀、分散,避免刀盘应力过度集中。

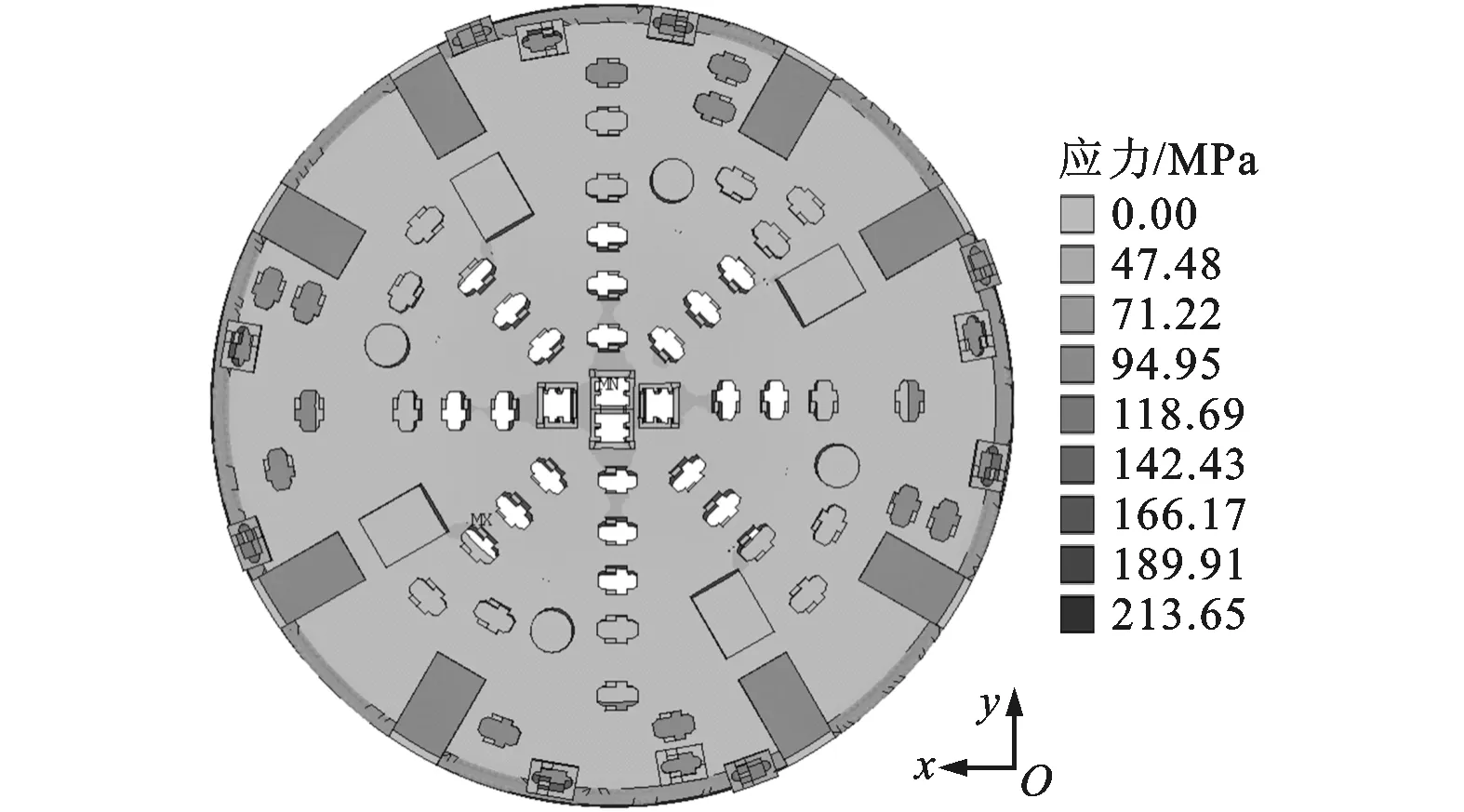
图21 平面刀盘von Mises等效应力分布云图

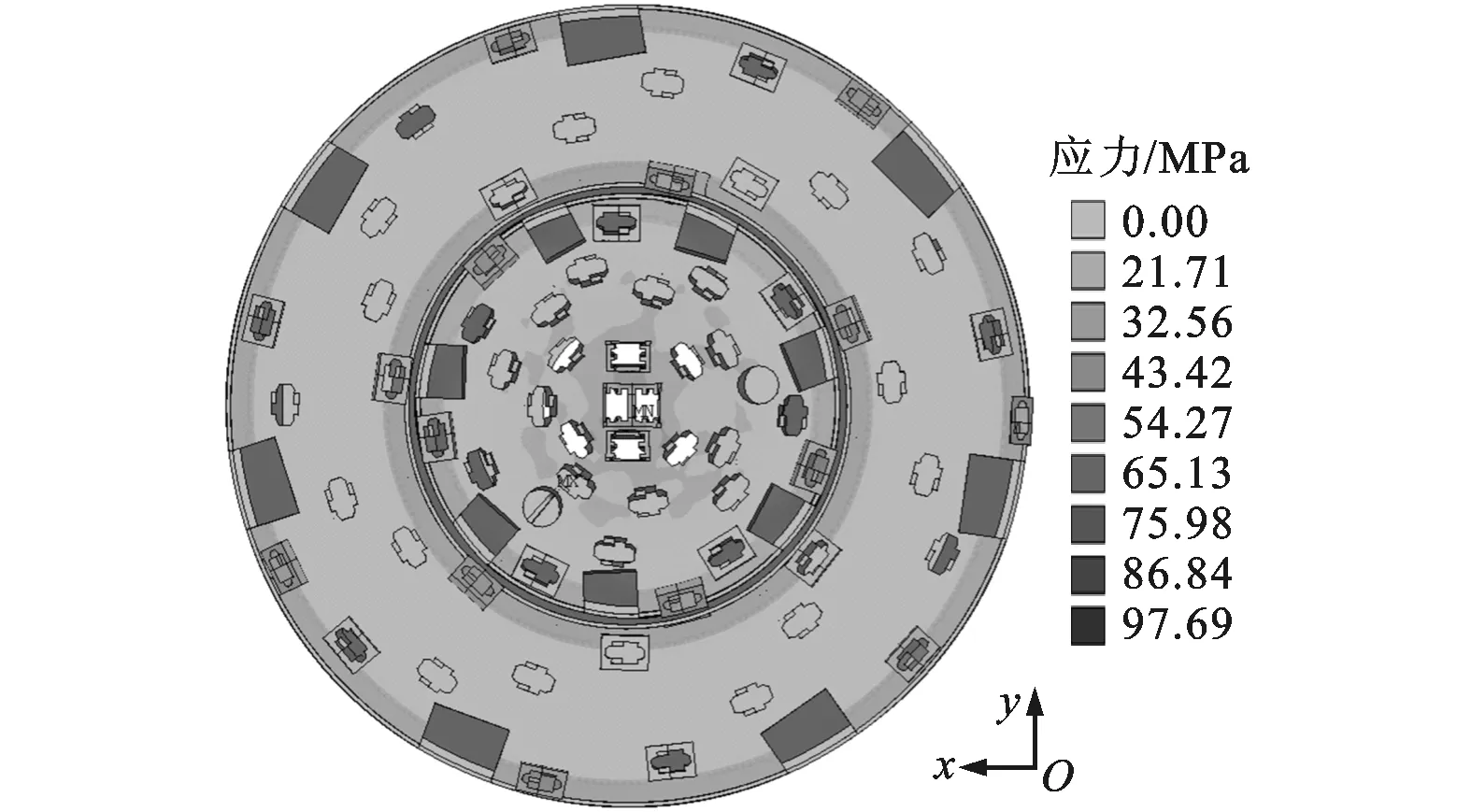
图22 两级刀盘von Mises等效应力分布云图

4 结 论

本文针对大直径硬岩TBM刀盘盘面变形大、主轴承偏载严重的问题,引入了一种两级刀盘结构形式,并采用灰关联分析的方法设计了两级刀盘结构。为此建立了复合岩层条件下平面刀盘和两级刀盘的受力计算模型,对比分析了两种刀盘的力学性能;建立了均一岩层条件下两种刀盘的有限元模型,对比分析了两种刀盘的变形和应力分布。结果如下。

(1)平面刀盘开挖复合岩层时,刀盘破岩总推力、扭矩随掌子面上岩石总体强度的增大而增大;对于给定的掌子面软、硬岩单轴抗压强度比,掌子面软、硬岩各占50%时,刀盘径向不平衡力和倾覆力矩最大;对于给定的掌子面软、硬岩面积比,两种岩石单轴抗压强度相差越大,刀盘径向不平衡力和倾覆力矩越大。

(2)相同的岩层条件(岩石强度、掌子面形状)和掘进参数(切深)时,两级刀盘的各级刀盘的破岩总推力、扭矩、刀盘径向不平衡力、刀盘倾覆力矩均比平面刀盘小。

(3)相同的岩层条件(岩石强度、均一掌子面)、掘进参数(切深)和刀盘结构参数(面板及支撑筋板厚度),两级刀盘的z向变形量比平面刀盘小,且变形量沿刀盘径向分布更为平缓,两级刀盘的最大应力比平面刀盘小,这是由于滚刀布局设计使得两级刀盘的滚刀分布更为均匀、分散,间接证明了灰关联分析方法进行滚刀布局设计的有效性。

[1] 王梦恕. 岩石隧道掘进机(TBM)施工及工程实例 [M]. 北京: 中国铁道出版社, 2004: 26.

[2] ROSTAMI J. Hard rock TBM cutterhead modeling for design and performance prediction [J]. Geomechanics and Tunnelling, 2008, 1(1): 18-28.

[3] 张红星, 张宁川. 803E掘进机刀盘振动问题浅探 [J]. 隧道建设, 2007, 27(6): 76-79. ZHANG Hongxing, ZHANG Ningchuan. Brief discussion on cutterhead vibration of type 803E TBM [J]. Tunnel Construction, 2007, 27(6): 76-79.

[4] HUO Junzhou, SUN Wei, CHEN Jing, et al. Disc cutters plane layout design of the full-face rock tunnel boring machine (TBM) based on different layout patterns [J]. Computers & Industrial Engineering, 2011, 61(4): 1209-1225.

[5] HUO Junzhou, SUN Wei, CHEN Jing, et al. Optimal disc cutters plane layout design of the full-face rock tunnel boring machine (TBM) based on a multi-objective genetic algorithm [J]. Journal of Mechanical Science and Technology, 2010, 24(2): 521-528.

[6] 耿麒, 魏正英, 杜军. 全断面岩石掘进机滚刀布置的优化方法 [J]. 西安交通大学学报, 2013, 47(9): 100-105. GENG Qi, WEI Zhengying, DU Jun. Cutter layout optimization method of full-face rock tunnel boring machine [J]. Journal of Xi’an Jiaotong University, 2013, 47(9): 100-105.

[7] 李震, 霍军周, 孙伟, 等. 全断面岩石掘进机结构主参数的优化设计 [J]. 机械设计与研究, 2011, 27(1): 83-90. LI Zhen, HUO Junzhou, SUN Wei, et al. Cutterhead structure optimal design of the full-face rock tunnel boring machine [J]. Machine Design and Research, 2011, 27(1): 83-90.

[8] 邓聚龙. 灰色系统基本方法 [M]. 武汉: 华中科技大学出版社, 1987: 112-138.

[9] KUO Y, YANG T, HUANG G. The use of grey relational analysis in solving multiple attribute decision-making problems [J]. Computers & Industrial Engineering, 2008, 55(1): 80-93.

[10]魏正英, 卢秉恒, 耿麒, 等. 一种用于全断面岩石掘进机的两级阶梯式刀盘系统: 中国, 20121057 99990 [P]. 2012-12-18.

[11]宋克志, 王本福. 隧道掘进机盘形滚刀的工作原理分析 [J]. 建筑机械, 2007(4): 71-74. SONG Kezhi, WANG Benfu. Operation principle analysis of disc cutter on TBM [J]. Construction Machinery, 2007(4): 71-74.

[12]刘景春, 贾寒飞, 张丽华. 全断面岩石掘进机刀盘简介 [J]. 重工与起重技术, 2006, 10(2): 1-4. LIU Jingchun, JIA Hanfei, ZHANG Lihua. Brief introduction to the cutterhead of full-face rock tunnel boring machine [J]. Heavy Industrial & Hoisting Machinery, 2006, 10(2): 1-4.

(编辑 赵炜 葛赵青)

Comparison of Mechanical Performances Between the Two-Stage Cutterhead and the Flat-Face Cutterhead for Rock Tunnel Boring Machine

GENG Qi1,WEI Zhengying1,MENG Hao1,ZHUO Xingjian2,JIA Lianhui2,HE Fei2,CHU Huali1

(1. State Key Laboratory of Manufacturing System Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. China Railway Engineering Equipment Co., Ltd., Zhengzhou 450016, China)

In order to overcome the drawbacks that large cutting load and eccentric load on the TBM’s large diameter (>10 m) flat-face cutterhead that will cause excessive deformation of the cutterhead and damage of the main bearing, a two-stage cutterhead was introduced. The two-stage cutterhead was designed in grey relational analysis method based on the flat-face cutterhead applied in West Qinling tunnel project. The mechanical performance analysis models of the flat-face cutterhead and the two-stage cutterhead under the mixed-face rock ground condition were built to compare the cutterheads’ rock cutting thrusts and torques, as well as the eccentric forces and moments. And finite element models of the two cutterheads under uniform rock ground condition were built to compare the cutterheads’ deformation and stress distribution. The results show that the rock cutting thrust, the rock cutting torque, the eccentric force and moment, the deformation and maximum stress of the two-stage cutterhead are smaller than that of flat-face cutterhead, which illustrates that the rock cutting loads are distributed into two stages of the cutterhead, and at the same time, the stiffness of the cutterhead is increased and the stress concentration and eccentric load of the cutterhead were also decreased.

full-face rock tunnel boring machine; two-stage cutterhead; flat-face cutterhead; mixed-face rock ground

2014-06-05。 作者简介:耿麒(1989—),男,博士生;魏正英(通信作者),女,教授,博士生导师。 基金项目:国家重点基础研究发展规划资助项目(2013CB035402)。

时间: 2014-12-30

网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20141230.0823.004.html

10.7652/xjtuxb201503019

TU94

A

0253-987X(2015)03-0121-08