多场景智慧高速公路的交通气象观测站点布设

张昕冉，孙洪运，张立涛

(山东理工大学 管理学院，山东 淄博 255000)

2021年《中国可持续交通发展报告》中指出，截至2020年底，我国公路总里程达到519.8万km，其中高速公路里程为16.1万km，国省干线公路和农村公路相互衔接，形成了四通八达的公路网络。在新一代信息技术革命的背景下，积极推进智能交通基础设施建设，打造智慧高速已成为未来发展的必然趋势。作为智慧高速公路交通气象信息系统的重要组成部分，交通气象观测站可以对道路沿线的交通气象环境进行实时监测，并能及时、准确地提供预报预警信息。通过研究站点选址的各种定性、定量方法，可以有针对性地为不同路段提供本地化、个性化的布设方案，提高监测系统的可靠程度，为更多的出行者提供更加优质的交通气象服务。目前，国内外一些专家学者对公路交通气象观测站的选址布设问题开展了研究。吴建波[1]根据路面温度的空间分布特征，采用热谱地图技术为京沈高速公路四方桥到万家段的站点布设提供了建议。吴杨等[2]考虑了灾害性天气的特点及各类气象要素对高速公路的影响，采用模糊熵和层次分析法建立评价模型，并以杭金衢高速公路的站点布设为例进行了实例分析。AL-KAISY等[3]考虑地理覆盖因素，提出了一个优先排序模型，并将其应用在蒙大拿州的样本站点上证明了该模型的实用性。YANG等[4]选择了3个标准对候选点的优先级进行排序，包括是否安装闭路电视摄像机、冬季交通事故数量以及年平均日交通量，并将这种决策支持方法应用在了韩国特别容易下雪的路段。ERIKSSON等[5]考虑了地理坐标、海拔高度、到海岸的距离等，采用多元回归分析研究了瑞典南部的站点布设问题。ZHAO等[6]考虑了年平均降雪量、年平均日交通量以及新建站点到现有站点的距离3种因素，建立了一个线性模型，确定了纽约州(纽约市除外)主要公路沿线的站点布设位置。KWON等[7]考虑了路面状况、降水类型，利用区域化随机变量为不同的气候区域开发了特定的半变异函数，并结合加拿大安大略省现有站点网络说明了该方法的应用。FETZER等[8]考虑车辆行驶里程、覆盖区域、电力和维护设施的可用性等因素，建立了多目标优化模型并使用修正ε约束法得到了一个非劣解集。针对多目标优化模型的求解，有理想点法、约束法和构建Pareto解集等。前2类方法主要将多目标问题转化为单目标问题，这种先决策后搜索的寻优模式在一定程度上降低了算法的求解难度，但破坏了多目标优化问题本身的物理意义。而Pareto 解集能够提供多种有效选择，更有利于决策者根据不同偏好进行决策[9]。进化算法如粒子群算法、遗传算法，由于其优异的性能得到了广泛的应用。黄川等[10]设计了多目标粒子群算法求解其构建的混合整数规划模型，优化了VTS雷达站的选址配置。胡文发等[11]用邻域拓扑结构改进了粒子群算法，求解了其提出的绿色建筑前期设计阶段多目标优化模型。田文等[12]运用带精英策略的非支配排序遗传算法(NSGA-II)求解了多目标非线性0-1整数规划模型，有效解决了航班航迹和时隙资源分配的问题。王宁等[13]使用改进的增强帕累托进化算法(SPEA-II)求解了多目标选址覆盖模型，提出了一种考虑均衡性和效益的消防站选址方法。上述文献主要是在既有公路交通气象观测站网上再优化布设，对于时空气象条件特征、年平均日交通量、天气相关交通事故特征的分析最多，关注交通气象监测覆盖的时空范围，但忽视了传感器故障和监测系统的可靠性。新建智慧高速公路由于应用场景的多元化、智能化和复杂性特点，需要更加有针对性的公路交通气象观测站布设方法。本文考虑新建智慧高速的3种应用场景，建立多目标优化模型并应用带精英策略的非支配排序遗传算法求解，得到站点布设的候选方案，以期为未来交通气象观测站的规划建设提供参考。

1 问题描述

一方面，智慧高速公路的应用场景包括车路协同和自动驾驶、全天候通行和主动交通管控以及伴随式信息服务等。山东省交通运输厅印发的《智慧高速公路建设指南(试行)》[14]指出，车路协同与自动驾驶系统宜由路侧感知设备、高精度地图以及高精度定位等组成，其中交通气象监测设备的布设间距宜小于15 km，并且能够监测能见度、路面结冰等天气状况。为保障全天候通行，应构建交通气象监测预警、交通安全防护诱导等系统，使用主动融冰除雪措施，提高恶劣天气条件下的出行质量。应能基于交通状态、路面状况以及气象条件，采取车道控制、车型控制等主动交通管控措施。对于出行的全过程，应能通过高速公路沿线信息发布设施、移动终端、车载终端等方式，提供实时的信息服务。这些新场景对交通气象站点布设提出了更高的时空和精度要求。另一方面，在其布设的过程中，最大布设个数、维修中心到候选点的距离、交通需求等常规因素都会对选址及传感器配型结果产生影响。施工材料及传感器类型的选择、候选站点的设计使用年限、工作人员到达维修地点的距离长短，会产生不同的固定建设和维护成本。

对于智慧高速公路而言，还需要考虑道路天气信息系统的可靠性。在传感器的使用过程中，不可避免地会发生故障，只有对某些需要重点监测的路段进行多重覆盖，才能保证在一个传感器发生故障时，其他传感器仍能对其实现有效监测。同时，候选站点在全生命周期内所能覆盖路段的总车辆里程数也是需要讨论的问题，更高的车辆里程数意味着站点能够为更多的需求者提供交通气象服务。

综上，本文创新性地提出由建设运营总成本最小、所选站点组成系统的可靠性最大和所覆盖路段的总车辆里程数最大组成的3个目标，提出一个多目标优化问题。场景需求和影响因素影响站点布设的逻辑关系如图1所示。

图1 场景需求和影响因素对站点布设的影响分析Fig.1 Analysis of the impact of scenario requirements and influencing factors on site layout

2 模型构建

2.1 模型假设和参数设置

模型假设如下。

假设1：不同智慧应用场景的服务要求用多重覆盖的次数替代，更高的覆盖次数可以提供更高的监测精度。

假设2：交通气象观测站覆盖范围和传感器可靠性均与天气类型无关，取多种天气综合水平作为传感器类型划分的标准。

假设3：交通需求已知。新建智慧高速公路多周期交通需求是离散的，高速公路腹地区域的经济、技术和社会发展水平等因素均会对其产生影响。

模型参数设置如下。

I为交通气象观测站候选点集合，共有|I|个候选点；L为路段单元集合，整条路段共划分为|L|个路段单元；Il为能够覆盖路段单元l的交通气象观测站集合，l=1, 2, …, |L|；Li为能够被交通气象观测站i覆盖的路段单元集合，i=1, 2, …, |I|；La为应用伴随式信息服务的路段单元集合；Lb为应用全天候通行、主动交通管控的路段单元集合；Lc为应用车路协同、自动驾驶的路段单元集合；K为传感器类型集合，共有|K|种传感器；xi为0-1变量，若交通气象观测站候选点i被选中，则xi=1，否则为0；yik为0-1变量，若交通气象观测站候选点i被选中且选用k型传感器，则yik=1，否则为0，k=1, 2, …, |K|；λik为交通气象观测站i选用k型传感器时的监测概率；μl为路段l被监测的概率；C为建设维护交通气象观测站的总成本；R为交通气象观测站的可靠性；U为规划时间内交通气象观测站覆盖路段的总车辆里程数；ci为站点i的固定建设成本；sk为配置k型传感器的成本；cm为每年每单位km维护成本；P为规划时间；Dmi为交通气象观测站i与其最近维修中心的距离；Ailt为能够被交通气象观测站i覆盖的路段单元l在第t个周期的年平均日交通量；dl为路段单元l的长度；Q为规划时间内允许建设的交通气象观测站的最大数量；dij为两站点间的距离；D为两站点间的建议最小距离。

2.2 路段单元被监测的概率计算

至少有一个交通气象观测站能够监测路段单元l才能保证其被有效监测，路段单元l被监测的概率μl为：

2.3 目标函数及约束条件

模型目标函数为：

约束条件为：

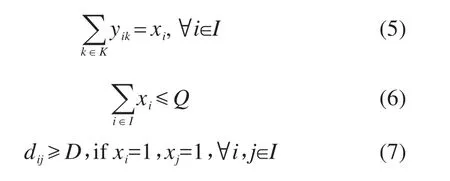
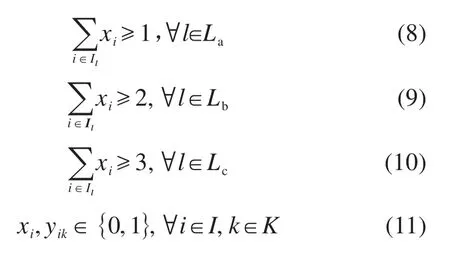
模型中，目标函数(2)表示总成本最小，第1部分为初始安装成本，第2部分为传感器成本，第3部分为维护成本；目标函数(3)表示可靠性最大；目标函数(4)表示5年为一周期，在站点的全生命周期内所覆盖路段的总车辆里程数最大；约束条件(5)表示若候选点被选中则配置一种类型的传感器，若未被选中则不配置传感器；约束条件(6)表示所建站点的数量不超过允许建设的最大数量；约束条件(7)表示两站点间的距离不小于建议最短距离；约束条件(8)表示若路段单元l属于应用伴随式信息服务的路段，则至少有一个能够覆盖路段单元l的候选点被选中；约束条件(9)表示若路段单元l属于应用全天候通行、主动交通管控的路段，则至少有2个能够覆盖路段单元l的候选点被选中；约束条件(10)表示若路段单元l属于应用车路协同、自动驾驶的路段，则至少有3个能够覆盖路段单元l的候选点被选中；约束条件(11)表示0-1变量约束。

3 求解算法

本文构建的模型为非线性多目标整数优化模型，各目标之间存在冲突，难以得到使3个目标同时达到最优的解，只能寻找非劣解。针对此模型的特点，宜采用启发式算法进行求解。带精英策略的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm II, NSGA-II)是由DEB等[15]提出的一种基于非支配排序的多目标进化算法，其优化效率性能比普通遗传算法、粒子群算法等更好。NSGA-II在NSGA的基础上进行了改进，采用快速非支配排序算法，合并了父代和子代种群，保留了更多的优秀个体，使用了拥挤度和拥挤度比较算子，不再需要人为指定共享参数，引入了精英策略，使得优良个体不会被剔除，从而降低了算法的复杂度，保证了种群的多样性，提高了运算的速度和结果的精度。其具体求解步骤如下。

3.1 染色体编码

本文的智慧高速公路交通气象观测站布设问题是一个离散问题，因此采用了二进制编码方式对染色体进行编码。染色体的长度等于候选点数量与每个候选点对应传感器类型的和，用x1,x2, …,x|I|表示候选点1, 2, …, |I|表示是否被选中；y11,y12, … ,y1|K|,y21,y22, … ,y2|K|, … ,y|I|1,y|I|2, … ,y|I||K|表示候选点对应的某类传感器是否被选中，取值均为0或1。例如用表1代表一条染色体，x1和y11取值为1，y12, …,y1|K|取值为0，表示候选点1被选中且配置第1种类型的传感器；x2,y21,y22, …,y2|K|取值为0，表示候选点2未被选中。

表1 染色体编码Table 1 Chromosome coding

3.2 确定初始种群并计算适应度

随机产生一条染色体并判断其可行性，若可行则予以保留，否则将其删除，直到染色体的数目达到设定的种群规模。按照帕累托分级和拥挤距离进行个体的适应度计算，并按从大到小的顺序选择个体保留到下一代。

3.3 交叉和变异

将染色体进行随机配对，并按照设定的交叉概率选择对应的基因进行互换。变异采取0-1变异，即按照设定的变异概率选择染色体上的某一点，将取值为1的变为0，取值为0的变为1。

3.4 终止条件

将设定的最大进化代数作为算法的终止条件，当达到最大进化代数时，停止算法的迭代。

4 算例分析

4.1 算例介绍及参数设置

本文选取正在建设的潍青高速主体部分作为研究对象，介绍所提出方法的应用。济青中线是继济青北线和南线建成通车之后，于2020年开工建设的连接济南和青岛的又一重要通道，是山东省第一条新建智慧高速公路项目。潍青高速是济青中线潍坊至青岛段，按照双向6车道的高速公路标准修建，是济青中线的重要组成部分。

如图2所示，潍青高速主体部分大体呈东西走向。在本文的研究中，将全长81 km的路段以3 km为一段划分为27个路段单元，每个路段单元由圆点之间的线段表示，自西向东依次编号为路段单元1，路段单元2等。在整条路段中有多处匝道，选取路段单元11中匝道西侧的路段划分点和路段单元20中匝道东侧的路段划分点(分别位于自起点起30 km和60 km处)将整条路段划分为3条路段。假定路段Ⅰ为应用全天候通行、主动交通管控的路段，由路段单元1到路段单元10组成；路段Ⅱ为应用车路协同、自动驾驶的路段，由路段单元11到路段单元20组成；路段Ⅲ为应用伴随式信息服务的路段，由路段单元21到路段单元27组成。在路段Ⅰ中由整条路段的起点开始自西向东每隔10 km设置一处智慧高速公路交通气象观测站候选点；在路段Ⅱ中自30 km处开始自西向东每隔5 km设置一处候选点；在路段Ⅲ中自60 km处开始自西向东每隔10 km设置一处候选点，共设置12处候选点，由图中三角形表示。假定在30 km和81 km处分别有一处维修中心，用正方形表示。

图2 潍青高速主体部分Fig.2 Main part of Weiqing Expressway

在本算例中，假定两站点间的建议最短距离为5 km，允许建设的最大站点数为7个，配置传感器的覆盖半径为15 km，各站点的固定建设成本(包括施工材料成本等)为5万元，每年每单位千米维护成本(包括燃油消耗成本、人工成本等)为0.035万元，规划时间为15 a(5 a为一周期，共包括3 个周期)[16−17]。

济青北线位于济南、淄博、潍坊北部，中线位于南部。在济青中线建成之后，由城市中心向两侧分流，可以有效缓解当地的交通拥堵问题。分别计算路段Ⅰ，Ⅱ和Ⅲ的年平均日交通量，并以此作为各自包含路段单元的年平均日交通量。在第1周期内，由于道路新建，所承载的年平均日交通量都比较少；在第2和第3周期内，由济青北线和济青南线转移到中线的车辆数逐渐增加。假定路段Ⅱ在第1周期内的年平均日交通量相比于其他2个路段少，但随着经济的不断增长、技术的创新发展，路段Ⅱ的服务水平逐渐提高，交通量逐渐高于其他2个路段，在总规划时间内的年平均日交通量也高于其他路段。各路段在不同规划时间内的年平均日交通量如表2所示。各候选点与其最近维修中心的距离、不同类型传感器的成本和监测概率分别如表3和表4所示。

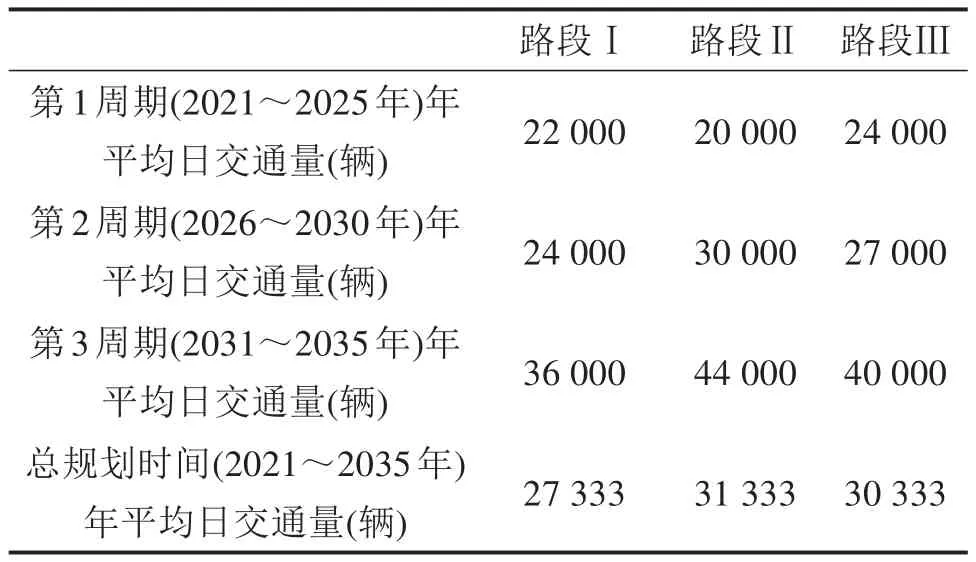
表2 各路段在不同规划时间内的年平均日交通量Table 2 Annual average daily traffic volume of each road section in different planning periods

表3 各候选点与其最近维修中心的距离Table 3 Distance from each candidate site to its nearest maintainment center

表4 3种类型传感器的成本和监测概率Table 4 Costs and monitoring probabilities of three types of sensors

4.2 计算过程及求解结果

在PyCharm中进行编程计算，目标维数为3，用F1表示总成本(万元)，为最小化目标；F2表示可靠性，为最大化目标；F3表示总车辆里程数(百万千米)，为最大化目标。决策变量维数为48，其中x1,x2, …,x12表示候选点1, 2, …, 12是否被选中；y11,y12,y13,y21,y22,y23, … ,y121,y122,y123表示每个候选点对应的3种传感器类型是否被选中，取值均为0或1。设置种群规模为100，最大进化代数为200，交叉概率为0.9，变异概率为0.02，三维目标的Pareto前沿如图3所示。为直观显示求解结果，将此三维坐标图中的每两维对应关系展示在二维坐标图4～6中。可以看出F1-F2Pareto前沿呈分开的2条曲线，符合经典的形状，而F1-F3Pareto和F2-F3Pareto前沿呈分开的2条直线，这是因为所有的路段单元全覆盖，所以总车辆里程数只有2个水平。

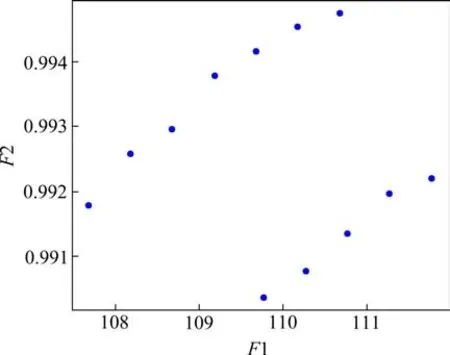
图4 F1与F2 Pareto前沿Fig.4 Pareto frontier for F1 and F2

由图3可知共得到12个非劣解，且不存在使每个目标都能达到最优的解，各非劣解之间不存在支配关系，决策者可以根据自己的偏好选取一个解作为布设方案。本文以图3中方块圈出的解为例，此非劣解对应的总成本为109.175万元，可靠性为0.993 79，总车辆里程数为31 809.75百万km，最终的选址结果可以满足本文提出的约束条件。在12个交通气象观测站候选点中选出了7个点，并为每个选出的点配置了一种类型的传感器，具体选址结果及传感器类型如表5所示，如候选点1被选中且配置传感器类型ESS-III，候选点3未被选中。选出的布设位置在图7中用三角形表示。

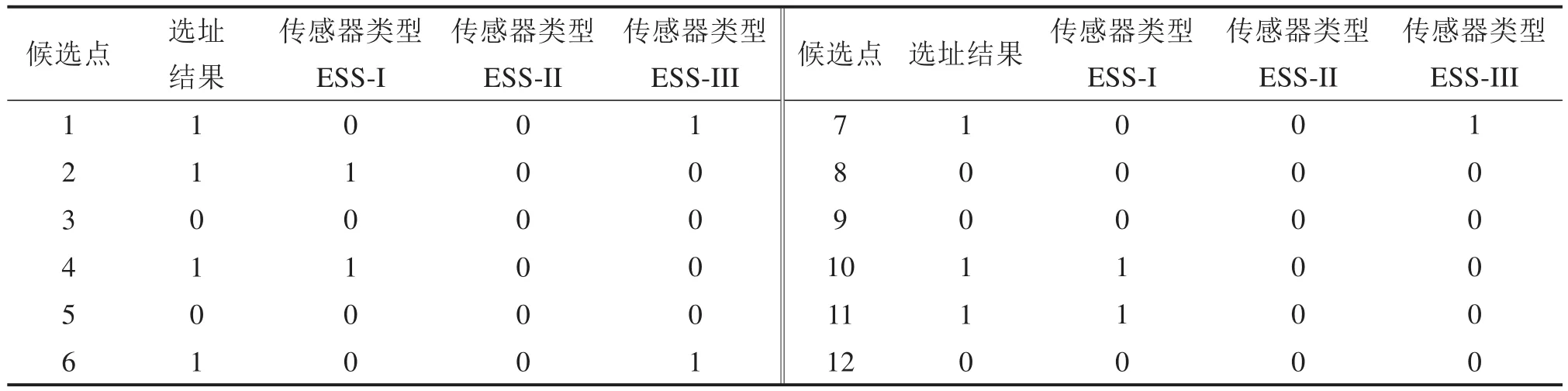
表5 选址结果及传感器类型配置Table 5 Site selection results and sensor type configuration

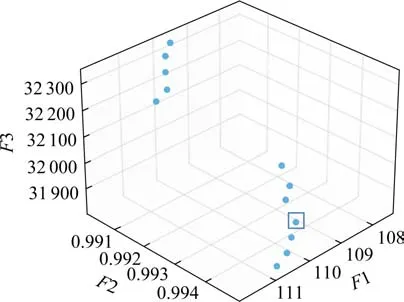
图3 三维目标Pareto前沿Fig.3 Three-dimensional objectives’ Pareto frontier

图7 一个交通气象观测站布设推荐位置Fig.7 One recommended locations of road weather information system stations

4.3 Q取值对目标值的影响分析

规划时间内允许建设的交通气象观测站的最大数量Q的不同取值对应着不同的目标函数值。计算程序运行一次得到的各个非劣解对应目标函数值的平均值，作为该次运行得到的目标函数值。将程序运行10次，取10次运行的目标函数平均值作为该Q值下每个目标函数的取值。分别取不同的Q值，当Q≤6时，无可行解；当Q取7，8，9，10和11时，对得到的目标函数值进行标准0-1变换，绘制出不同Q下的目标函数值变化如图8所示。

图5 F1与F3 Pareto前沿Fig.5 Pareto frontier for F1 and F3

图6 F2与F3 Pareto前沿Fig.6 Pareto frontier for F2 and F3

由图8可得，总成本、可靠性和总车辆里程数3个目标值均随着Q值的增加而增加。总成本在Q由7增加到8时增加的速度最快，之后逐渐放缓，在由10增加到11时略有回升，但均小于由7增加到8时的增速。可靠性的增速在Q由7增加到8和由8增加到9时均较快，而在9到10和10到11时增速较慢。由此可知，Q取值增加到8和9时对可靠性的增加影响较大，而增加到10和11时，对可靠性的增加作用较小。总车辆里程数在Q由7增加到8时的增速较快，之后的增速变化不大。决策者可以根据自己的偏好确定Q的取值。

图8 不同Q下的目标函数值Fig.8 Objective function values with different Q

5 结论

1) 以潍青高速的主体部分为例，使用本文构建的多目标优化模型及NSGA-II得到了一个非劣解集，并以其中一个非劣解作为布设方案，在12个候选点中选出7个布设位置，验证了模型和算法在解决智慧高速公路交通气象观测站选址布设问题中的可行性。

2) 总成本、可靠性和总车辆里程数3个目标值均随着Q值的增加而不同程度地增加。当最大布设个数由9增加到10和11时，对可靠性的增加作用较小。

3) 在未来的研究中可以加入更多的智慧高速公路应用场景，对于不同路段所需的覆盖次数和交通需求预测还需要进行进一步讨论。同时，对于天气时空差异以及与网联车载移动感知器的协同布设问题还需要进一步研究。