债券信用溢价的共同因子与结构变化：基于机器学习方法

熊海芳，刘 跃，刘天铭

（东北财经大学 金融学院，辽宁 大连 116025）

一、引 言

债券和股票均是公司融资的重要渠道，也是基金经理投资的主要资产，因此，应用因子模型对公司债券信用溢价的截面差异进行研究，有助于投资者提高对债券风险溢价因素的理解和风险管理。对于公司债券市场，已有文献多探讨影响公司债券信用溢价的因素，如宏观经济、市场利率、发行主体特征等。［1－3］但是这些研究对债券因子组合以及债券信用溢价共同因子模型的研究比较少。因此，本文将构造多个债券共同因子，进而考察其对公司债券信用溢价的解释能力。

对于公司债券信用溢价在截面上存在的差异，已有研究从不同角度进行了分析，发现多个具有解释力的影响因子。现有因子主要分为以下几类：第一类，债券特征因子，比如债券流动性、发行主体信用评级、债券信用评级、发行规模等。［4－6］由于我国社会信用体系建设并不健全，外部评级基本集中于AAA级和AA级，因此，单纯依赖信用评级对公司债券信用溢价进行分析效果不佳。［7］第二类，债券市场因子。有学者发现与股票市场类似，债券市场中也存在动量因子，［8－9］债券持有人对债券下行风险更为敏感，下行风险是一个有效影响因子。［10］流动性和波动率因子在公司债券定价中也有强解释能力。［4，6，10］第三类，股市因子。一些研究利用股票和债券市场因子来探讨其对同期或未来的债券收益的影响，如Fama－French三因子。［11－12］第四类，公司特征因子，这类因子主要与公司基本面有关，比如其盈利和投资。［13］由于在我国发债企业中包含部分未上市企业，其信息披露不完善，多数财务数据无法获取，因此，本文在构建我国债券市场共同因子的过程中并未考虑公司特征因子。部分研究发现市场利率、债券久期等因子会影响单个债券收益率，［5，14］本文在研究过程中主要通过截面视角对因子进行研究和检验，需要进行久期匹配并引入债券市场因子，因此不再考虑宏观因子、市场利率、久期及利率期限结构因子。根据文献研究、国内数据的可获得性和研究需要，本文在构建债券组合的基础上，综合规模、动量、流动性、波动率和下行风险等考察我国公司债券风险溢价的共同因子。此外，2015年1月16日《公司债券发行与交易管理办法》（下文简称“2015‘办法’”）的推出对债券市场影响巨大，公司债市场容量明显增大，各子样本内公司债数量增加。因此，为了探讨2015年1月之后市场扩容的影响，本文进一步以2015年1月为界研究公司债券信用溢价因子的解释力度是否存在结构性变化。

研究影响公司债券信用溢价的共同因子，需要探讨如何选择有效因子。最常见的做法是将因子加入线性模型，通过回归对比截距项。这样做尽管直观，但只考虑了因子的线性影响。随着机器学习的发展，有学者开始尝试将机器学习引入因子模型，利用正则化稀疏学习等方法来进行因子选择。Breiman提出了适用于这类问题的集成学习算法——随机森林。［15］Patel等发现随机森林方法在股指趋势预测中有一定优势。［16］鉴于此，本文将LASSO等机器学习算法应用于债券信用溢价因子模型，比较不同模型的解释能力并探讨因子是否存在结构变化。

与已有研究相比，本文的创新在于：第一，从债券市场、股票市场、债券特征等角度综合构造公司债券信用溢价的共同因子，这从理论上为探讨我国公司债券信用溢价的决定因素提供了新的解释；第二，除了使用传统线性回归模型外，本文综合利用多种机器学习方法对因子回归模型进行变量选择，对不同方法的精确度、稳定性进行比较，分析共同因子存在的结构变动情况，进一步证实机器学习方法在我国公司债券市场的可行性与实用性。

二、公司债券信用溢价因子与多因子模型

（一）市场因子

要构建公司债券信用溢价的单因子模型，通常根据单因子值对资产进行排序，然后分组构建组合，直接检验最高和最低两组差异的显著性。在判断因子有效性时还可以进行CAPM回归。债券组合CAPM回归中需要构建市场因子，一是像构建股票因子一样采用多空组合方法计算，二是参考Houweling和Van Zundert通过做多策略构建债券市场因子，这是因为债券市场中做空难度较大，做空成本较高。［6］回归方程如式（1）所示：

其中，Rt和DEFt分别代表因子和债券市场组合在t时刻的信用利差，即CAPM－alpha。

（二）债券特征因子

已有研究发现，债券的发行规模、发行期限以及信用评级均会对公司债券信用溢价产生影响。规模因子用债券流通市值总额表示，期限因子用债券久期表示，信用评级则通过计算理论信用利差及其与债券实际信用利差的差值来衡量。经验研究中通常采用公式（2）构造公司债券价值因子组合。［17］

在式（2）中，CSi为该月公司债券信用利差；Dir是代表债券评级的虚拟变量；Mi代表债券久期。本文仅保留主要评级级别，将AAA＋、AAA－统一视为AAA，并以此类推，因此模型中评级虚拟变量个数为8个。这样做可以保证回归过程尽量减少自由度的损失。此外，公司债券自身特征还有久期利差因子，本文根据久期匹配对应国债计算债券的信用利差，这样做可以从信用利差中剔除久期的影响。

（三）债券市场特征因子

除了债券特征因子，本文还引入了债券市场特征因子，如动量、波动率、下行风险、流动性等。波动率因子组合通过计算收益率的历史波动率来构建，下行风险因子组合通过计算债券的历史累积收益率来构建。对于流动性因子组合，由于我国公司债券交易不活跃，多数债券的交易在时间序列上并不连续，故无法采用Bai等的流动性因子构造方法，直接采用债券日换手率进行构建。［10］对于动量因子组合，先将债券根据公式（3）计算各自的历史累积收益率并进行排序后，再构建组合。

其中，Pi，t和 Pi，t－1分别代表形成期期末和期初债券 i的日收盘全价，couponi，t为形成期内该公司债券的实际支付利息。

（四）多因子模型

1.基于债券的多因子模型。参考Houweling和Van Zundert、Bai等的做法，本文将公司债券共同因子以及债券市场因子一同纳入多因子模型。［6，10］在考虑了公司债券的共同因子和市场因子后，本文构建包含七个单因子的多因子模型，具体形式见公式（4）。其中，Ri，t为债券或组合i在t月的年化信用利差。DEFt为市场组合t月的信用利差，作为市场因子。size、value、momentum、volatility、downrisk和liquidity分别为规模因子、价值因子、动量因子、波动率因子、下行风险因子和流动性因子。

2.考虑股市的多因子模型。参考Franke等的做法，在公式（1）的基础上，加入股市因子构造多因子模型，以此检验本文构建的单因子组合收益在加入了股市多因子模型下是否仍具有无法解释的alpha收益，回归方程见公式（5）。［18］其中，MKTt、SMBt、HMLt为 Fama － French 三因子。

三、因子模型的机器学习方法

（一）基于LASSO族的稀疏学习方法

1.LASSO。LASSO通过正则化进行压缩估计，使得LASSO兼具变量选择和变量降维的功能。对于多因子回归模型，LASSO主要通过对公式（6）的最小值求解。其中，第一项为回归方程的残差平方和，第二项为压缩惩罚。为使公式（6）取值最小，惩罚项的存在会使解释能力弱的变量参数估计值压缩为零，从而起到变量选择的作用。在分析公司债券信用溢价因子模型时，为防止过拟合，需要对λ值进行设定。

2.自适应LASSO。自适应LASSO加入最优化过程，通过公式（7）使各个变量回归系数具有自选择的特点。其中，为因子j回归系数的惩罚权重，γ＞0，通常将其设定为［1，10］的任一整数。为因子j在OLS中的参数估计值。与LASSO算法不同的是，自适应LASSO并不需要人为设定λ值。对于γ和λ的取值，均通过算法循环求解，以模型拟合均方误差最小为判断准则，采用十折交叉增加样本容量，从而得到各债券最优组合（λ*，γ*）及最优参数估计值。

3.弹性网络。LASSO使用的惩罚项为L1范数，弹性网络和LASSO类似，区别在于弹性网络是L1和L2范数的组合，具体形式如公式（8）所示。弹性网络仍通过对参数施加压缩惩罚进而实现变量选择的功能。弹性网络的优势在于：当模型自变量存在多重共线性问题时，OLS估计虽然无偏但方差膨胀，而弹性网络利用L2范数，泛化能力更好。

（二）集成学习方法

集成学习方法大致分为串行生成的序列化和可同时生成的并行化两类。其中第一类最常见的是Boosting算法，往往用于分类问题，但也有如XGBoost算法可用于回归。第二类算法不仅可用于分类也可用于回归，最常见的如Bagging和随机森林算法。［19］其中，随机森林算法是在Bagging算法的基础上加入了随机属性（因子）选择，因此，随机森林算法拥有较强的泛化能力和防过拟合能力。XGBoost作为一种集成学习方法，借鉴了很多随机森林算法的思想，最后结果根据多个可叠加树求和得到。对于一个存在m个特征的数据集，算法通过对每个“树”函数求和来输出预测结果，具体形式如式（9）所示：

其中，f（x）＝wq（x）为回归树模型，其结构与权重均通过学习确定，在整个学习过程中，需要对如下目标函数进行不断优化：

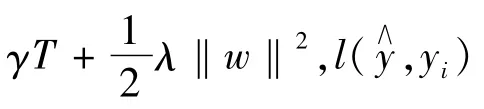
四、公司债券信用溢价的共同因子

本文以我国流通的公司债券为研究对象。由于2010年前公司债发行数量极少，样本代表性不足，故研究的时间区间从2010年开始。由于本文研究时国泰安数据库中Fama-French三因子月度数据更新至2018年6月，因此样本区间设为2010年1月～2018年6月。数据来源及预处理过程如下：（1）债券交易、评级数据均来自于锐思网站，剔除了含权债券，Fama－French三因子数据来源于国泰安数据库。（2）由于我国债券市场流动性较差，为了避免部分流动性极差债券带来的异常收益影响，剔除单只债券中月交易日不足10天的不活跃月份，保留的月份定义为有效交易月份。

2015“办法”后，公司债规模的扩大、发行增速的提高以及非公开债券发行的拓宽有利于提高债券流动性，进而降低债券流动性风险。2015“办法”建立了投资者适当性制度，设立资质条件过滤合格投资者，限制中小投资者的投资标的，从而改变公司债投资者的组成结构。为进一步探究2015“办法”对公司债券风险溢价的影响，本文以2015年为界研究公司债券信用溢价因子的解释力度是否存在结构性变化。

本文参考Houweling和Van Zundert的方法 计算信用利差。［6］根据债券久期匹配对应国债，将公司债到期收益率扣除匹配久期的国债到期收益率，所得即为该公司债的信用利差。通过匹配后计算的债券信用利差可以排除久期对信用利差的影响。将组合内债券信用利差按照等权重求平均值即可得到组合信用利差。由于我国债券市场上不存在衡量市场整体信用溢价的指标，本文以信用债市场上全部公司债构建市场因子。公司债券各因子的定义如表1所示。

表1 公司债券因子名称及其定义

（一）基于线性回归的单因子模型：公司债券特征与市场特征

将债券分别根据规模、价值、动量、波动率、下行风险、流动性因子对各个因子构建H－L（High minus Low）组合，通过观察相同因子下不同组合的信用利差差值判断因子有效性。进一步以2015年1月为界，探讨因子在2015年前后是否存在结构性变化。不同样本时间区间内单因子多空收益率（H－L组利用利差差异）表现如表2中Panel A～Panel C所示，完整时间区间下市场组合以及单因子持有做多组合表现如Panel D所示。从实证结果来看，动量因子对公司债券未来信用溢价解释能力较差，其在我国公司债市场上因子收益并不显著。①关于动量因子本文分别探讨了3、6、9、12个月不同动量形成期下单因子组合信用利差，由于文章篇幅有限，本文只汇报了3个月动量形成期的实证结果，其余形成期下H－L结果与3个月期结果类似，有兴趣的读者可向作者索取。规模、价值、波动率、下行风险、流动性五因子均可获得显著超额收益。

表2 不同时间区间下的单因子组合信用利差

2018年债券违约事件频发，2018年的违约债券数量已超过了2014～2017年的总和。除了违约风险增加，2018年还伴随着资管新规的推出以及去杠杆进程的推进，货币紧缩带来信用紧缩导致债券市场在2018年波动巨大。①本文实证同样发现2018年债券市场波动对债券收益率的影响较大，限于文章篇幅，相关实证结果并未列示，留存备索。为了剔除债券异常信用利差的影响，本文将研究的样本区间控制在2010～2017年。

（二）基于线性回归的多因子模型：股市因子与债券特征

基于公式（5）对公司债券信用溢价做多因子回归分析，发现在控制股市三因子后，债券单因子组合alpha仍在1%水平上显著为正②限于文章篇幅，经过股票市场多因子调整后的债券因子组合alpha的实证结果并未列示，留存备索。，即加入Fama－French三因子后的多因子模型不能解释各个债券单因子组合的信用利差，这与Houweling和Van Zundert、刘桂梅和杨晨的研究结论一致。［3，6］

综上可以发现，在我国债券市场中，规模因子、下行风险因子、价值因子、波动率因子以及流动性因子共5个共同因子，可以获得显著的因子收益，而动量因子收益不显著。不论是单因子检验还是在加入了Fama－French三因子后的多因子检验下，5个共同因子组合均存在显著alpha收益。基于以上结论，从公式（4）中剔除动量因子构建多因子模型。从单因子间相关系数可以看出③限于文章篇幅，因子的相关系数矩阵并未列示，留存备索。，不同共同因子间相关性不高，说明因子之间的关联性不强。

五、机器学习方法下公司债券因子模型与结构变化

（一）基于稀疏学习的多因子模型

本文利用5个有效共同因子及市场因子共6个因子，对每个公司债券分别基于LASSO、自适应LASSO做回归，通过统计各因子在全部样本公司债券回归中最优估计参数非零的个数，来对比单因子对公司债券信用溢价解释能力的差异。由于下行风险因子计算限制，本文使用2013年1月～2017年12月经前文条件筛选后保留的债券数据，在此基础上，仅保留至少有20个有效月的公司债券作为样本，共150只。尽管前提条件苛刻，保留的债券数据较少，但每只债券的日交易数据充足，信用利差数据更具真实性和代表性。两种算法下最优估计参数取值情况如表3所示。

表3 稀疏学习下各因子最优参数取值统计

在表3Panel A中展示了惩罚项系数λ为0.01的LASSO的参数取值统计。除去市场因子外，流动性因子参数估计值非零数量在全部样本债券中占比最高，其余5个因子非零比例均超50%。参数估计值均为0的公司债数量为0，均非零的公司债数量为44。在Panel B中，自适应LASSO通过对样本内数据交叉验证得到最合适的λ参数值。随着λ值增加，六因子最优参数估计值非零频率均出现下降，但仍十分显著。

（二）公司债券因子的结构变化：基于线性回归

为探索我国公司债券因子在2015年前后是否存在结构变化，借鉴传统的邹检验构建如下模型：

其中，Rit为债券i因子组合在第t月的年化信用利差；DEFt为市场组合在第t月的信用利差；Dt是代表时间的虚拟变量，2015年1月之后取1，否则取0；DtDEFt为时间虚拟变量与市场信用利差的交乘项。从实证结果来看，五个债券共同因子组合在各自的回归方程中，交乘项系数均显著大于0，说明公司债券因子在2015年前后存在结构变化。①限于文章篇幅，邹检验下公司债券单因子组合结构变化的实证结果并未列示，留存备索。

（三）公司债券因子的结构变化：基于稀疏学习方法

利用自适应LASSO方法，研究其是否可以发现公司债券因子中存在的结构变化。为保证每只债券均有充足样本数据，在每个样本区间仅保留有效交易月份不少于10个月的债券，经筛选2015年前后两个样本区间分别保留145只及120只公司债券。各样本区间最优参数估计值取值情况见表4。从表4中可以看出，2015年以前，规模因子解释广度最广，市场因子解释力度最弱。2015年以后，下行风险因子解释广度最广，规模因子解释力度最弱，其次是流动性因子，这点与流动性风险分组的表现相对应：2015年以来最低流动性风险分组的债券组合波动率明显升高，这会对参数估计产生影响。所有因子最优参数估计值均非零的公司债数量占比上升至10%。此外，利用弹性网络算法，即使在惩罚项增多的情况下，因子解释力度强弱及变化与自适应LASSO基本一致。②限于文章篇幅，弹性网络算法下各因子最优参数取值统计的实证结果并未列示，留存备索。因此，通过基于稀疏学习方法同样可以发现公司债券市场及其共同因子的结构变化情况。

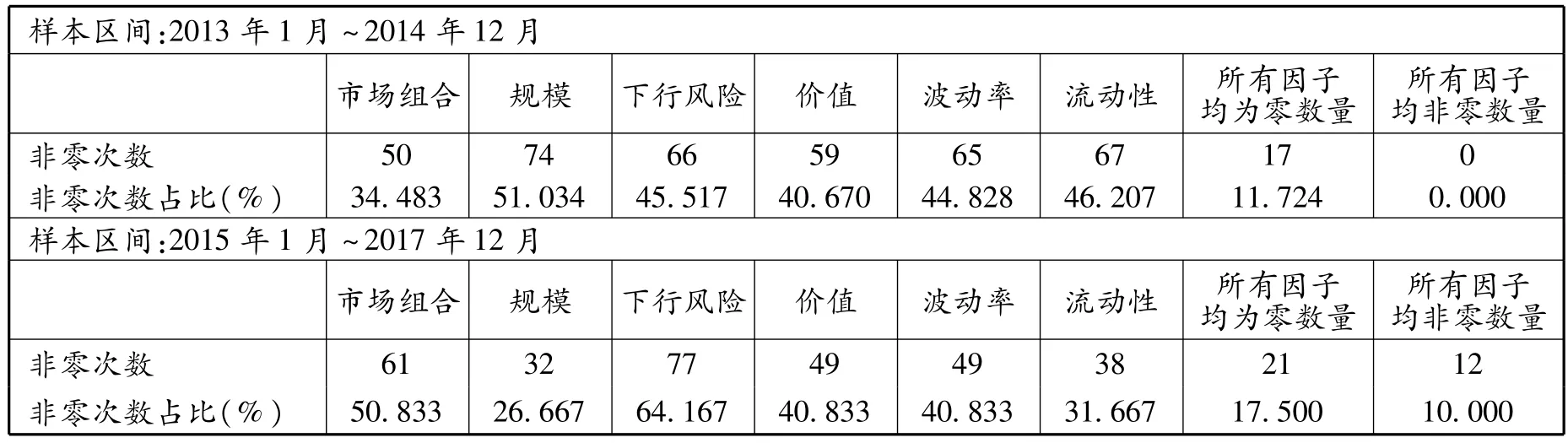
表4 自适应LASSO下各因子最优参数取值统计

（四）公司债券因子的结构变化：基于集成学习方法

利用集成学习中随机森林、XGBoost以及决策树三种方法，采用同前文相同的划分区间方式，分析整个时间区间内因子的重要性变化。两个子样本区间内债券信用溢价六因子在三种方法上的信息增益如表5所示。2015年以前，规模因子在决策树和随机森林方法中的信息增益最大，市场因子在XGBoost方法中的信息增益最大，其次为规模因子，波动率因子最小。2015年之后，三种模型中信息增益最大的因子分别为价值因子、下行风险因子和市场因子；规模因子在决策树和随机森林中的信息增益最小，XGBoost中流动性因子信息增益最小。

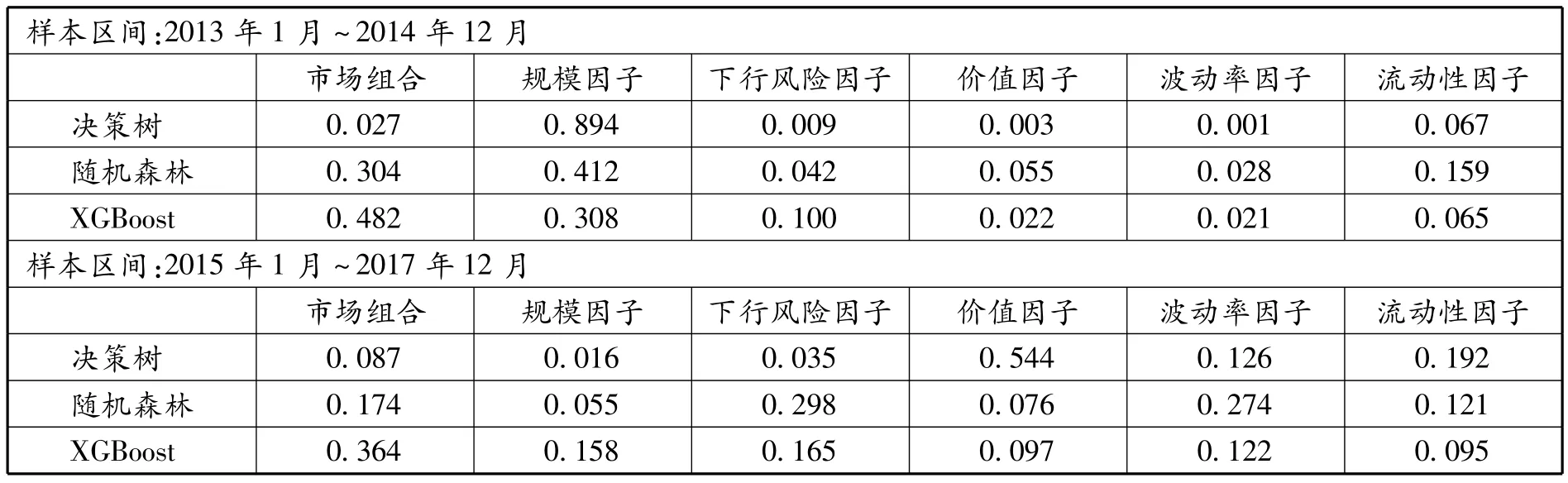
表5 债券信用溢价因子的信息增益

总的来看，不论线性回归、稀疏学习还是集成学习均可发现公司债券市场及其共同因子存在结构变化。利用基于稀疏学习的自适应LASSO、弹性网络，可以发现因子在公司层面上的结构变化情况，利用基于集成学习的随机森林等三种方法可以发现因子在样本区间层面的结构变化。经对比，2015年前，市场因子、规模因子、下行风险因子在稀疏学习中有较高的解释力度，前两者在集成学习中也有较高的信息增益，波动率因子在稀疏学习及集成学习中解释力度均较小；2015年后，市场因子、下行风险因子在稀疏学习及集成学习中对应的解释力度均较高，流动性因子在稀疏学习及集成学习中解释力度均较低；2015年前后，在两种稀疏学习方法中，流动性因子均明显下降，价值因子、波动率因子变动不明显，规模与下行风险因子在稀疏学习和集成学习中解释力度分别明显下降和上升。

（五）公司债券因子机器学习方法结果的比较分析

对比来看，机器学习方法下的实证结果与前文传统线性回归与邹检验结果基本一致。首先，在线性回归中加入惩罚项的稀疏学习方法中，因子不论在全样本还是分时期样本下依然具有显著解释意义；在集成学习方法中，共同因子在降低信息熵的过程中均提供了信息增益。这些结果说明机器学习方法下共同因子在解释公司债券信用溢价方面具有显著的解释能力，与基于线性回归的单因子和多因子模型结论一致。在理论上，这与资产定价的多因子模型是一致的。其次，稀疏学习和集成学习均可发现因子存在结构变化，这点与传统的邹检验结论一致。综合来看，机器学习方法下的实证结果与传统的线性回归结果基本一致，且提供了更丰富的信息，同时结构变化分析揭示了政策调整的影响，有效说明了机器学习方法结论的准确性和适用性。总体来看，机器学习算法结果比较符合公司债券投资的理论解释和我国的市场实践。

六、结 语

本文采用线性回归和多个机器学习方法对我国公司债券信用溢价的共同因子模型展开研究。结果发现：（1）在对2010～2017年债券市场信用溢价的截面差异进行解释时发现，规模因子、下行风险因子、价值因子、波动率因子以及流动性因子等5个共同因子可以获得显著的因子收益，而动量因子收益不显著，2018年债券违约和市场信用紧缩导致市场波动，因子模型的解释发生较大变化。（2）在单因子检验和加入了债券市场因子、Fama－French三因子后的多因子检验下，5个共同因子的做多组合均存在显著alpha收益，说明这5个因子是具有解释能力的。流动性因子组合对市场风险的β值较低，组合收益的波动率最小，说明该因子的逆周期防御功能较强。（3）本文构造了规模因子、价值因子、下行风险因子、波动率因子和流动性因子等5个共同因子模型，稀疏学习方法能够验证模型中5个因子的有效性。（4）利用邹检验和机器学习方法均能发现我国公司债券共同因子在2015年前后存在结构变化，机器学习方法比邹检验可以发现更多因子结构变化细节。（5）自适应LASSO对因子变动更为敏感，识别结构能力更强。基于集成学习的随机森林和XGBoost方法要比单纯的决策树算法好，在因子区分度上表现更明显。本文的结果证实截面共同因子在公司债券信用溢价中的解释作用以及机器学习方法在我国公司债券市场的实用性。

本文的发现具有较强的政策启示：机器学习算法可以在传统因子模型的基础上提供更多的有效信息，因此，可利用机器学习算法建立风险预警。此外，在公司债券市场的市场制度和环境改变过程中，可以利用机器学习算法识别其对市场的影响，防范化解潜在的系统性风险。