递推积分滑模变结构控制在有源电力滤波器中的应用
陈 聪
(中国石油天然气管道工程有限公司)
油气管道站场设有不间断电源UPS、 开关电源设备等,这些电力电子设备的使用会产生谐波电流,谐波电流又会对其他设备和电网会产生一定的威胁。 有源电力滤波器(APF)的原理为实时检测谐波电流,使逆变器输出同谐波电流幅值一致、相位相反的电流,以动态消除谐波电流,较无源滤波器具有动态滤波效果好的优点[1]。 而APF的滤波效果关键取决于补偿电流控制策略。
滑模变结构控制可以快速、频繁切换系统的控制状态, 而且它与电力电子开关器件的 “开-关”模式相似,本质都是开关型控制,同时滑模变结构控制具有较强的鲁棒性,在有源电力滤波器控制中得到了一定的应用。 笔者针对滑模变结构控制存在的跟踪静差问题, 提出一种递推积分PI控制算法来降低稳态误差,将该控制算法的输出作为滑模变结构控制的输入,形成多重变结构控制, 使得APF不但具有较快的响应速度同时可以减小稳态误差。
1 递推积分PI控制原理
为了使受控对象的输出无差别地跟踪给定信号,要求其控制器必须包含积分环节。传统的PI控制在被控量为缓慢变化的量或直流量时能够实现无差控制,但当被控量为快速变化的量或交流量时,如果采用传统的PI控制方法,会产生稳态误差[2]。 因为给定的谐波指令信号是各次谐波的叠加,是一种交流量,为此笔者提出一种基于离散信号迭代运算的递推积分PI控制算法代替传统的PI控制方法,用来消除稳态误差。
递推积分PI控制的输入可视为周期为20 ms的正弦量倍数的各种频率信号的叠加, 如图1所示。
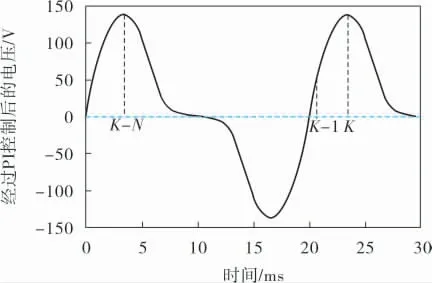
图1 递推积分PI控制的输入参考信号示意图
传统PI环节s域传递函数为:
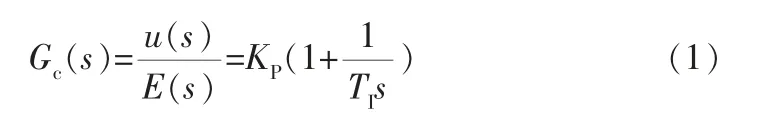
式中 KP——比例系数;
TI——积分时间常数。将其离散化得:
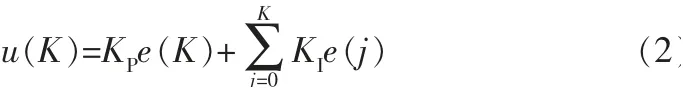
式中 e(K)——K时刻的误差采样值;
KI——积分系数;
u(K)——K时刻的控制器输出。
可见,传统PI算法是对误差进行逐点积分的[3]。
递推积分PI控制算法函数如下:
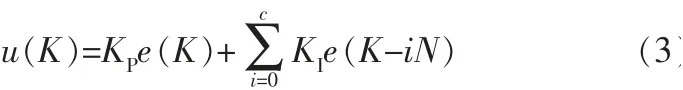
其中,c=K/N,取整。
该算法包含周期信息,按逐个周期对每个采样点的误差进行积分, 而传统PI控制没有包含周期信息,所以递推积分更精确。 对于误差e,每个周期中的相应采样点被积分, 这相当于使N个PI并行工作。
利用u(K)的增量形式可简化计算,在K-N时刻,由式(3)得:
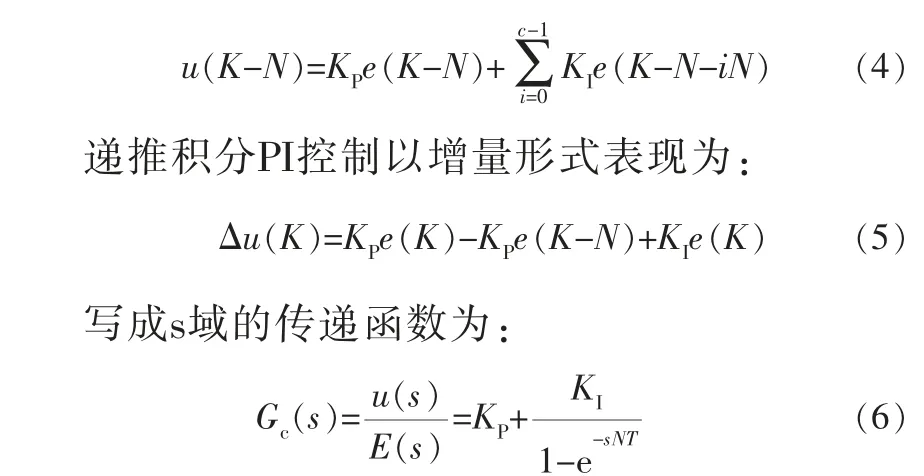
其中,T为采样时间间隔;NT=20 ms。
对于谐波电流的采样来说,按采样点的误差逐个周期积分比按误差逐点积分效果好,因为谐波是频率为50 Hz倍数的周期信号的叠加。
控制量uc(K)在s域的表达式为:
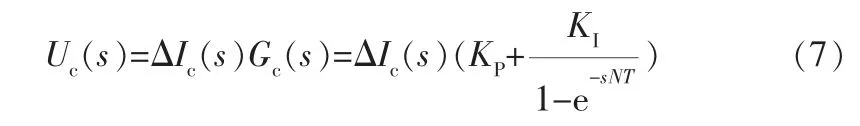
式中 ΔIc——谐波电流跟踪误差。
2 滑模变结构控制
2.1 三相三线制有源电力滤波器数学模型
对于三相三线制有源电力滤波器,引入变量Ki:

其中,i=a,b,c(380 V系统中的a、b、c三相)。
对此电路应用基尔霍夫电压定律[4],有:
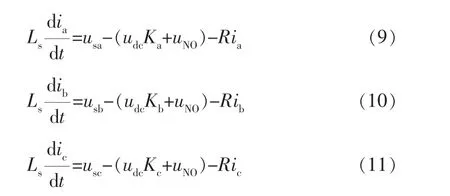
式中 ia、ib、ic——有源电力滤波器a、b、c三相发出的电流;
Ls——有源电力滤波器每相电感;
R——有源电力滤波器每相电阻;
udc——有源电力滤波器直流侧电压;
uNO——电源侧中性点O和逆变器公共端N之间的电压;
usa、usb、usc——电源侧每相电压。
假设三相电源对称,有:
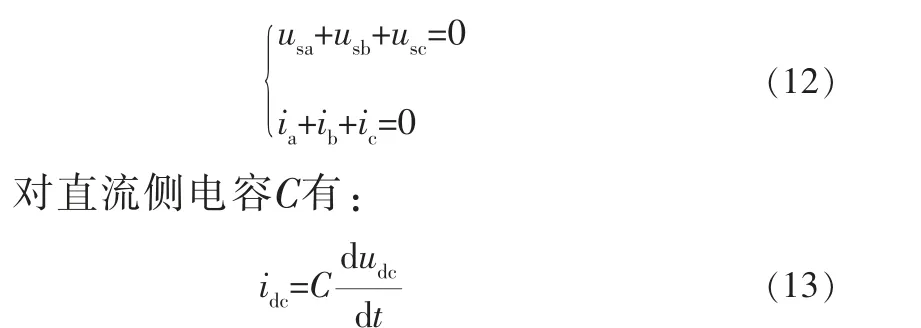
在电容的正极处采用基尔霍夫电流定律,得:

2.2 滑模变结构控制器设计

首先把APF滑模变结构控制切换的曲面设为si=ei=0, 通过判别当前跟踪误差在切换曲面的哪一侧选取相应的开关模式[5]。
一般采用等速趋近律来设定滑模变结构控制器,即:

同理可得Kb,Kc。
在选择逆变器时, 注意应满足Keq∈(-1,1),同时需选择合理的ε′使Ka∈(-1,1), 这个定理将控制Ka转换为用±1电平表示的PWM波。
根据滑模变结构控制理论,APF离散滑模变结构控制率Kx如下:
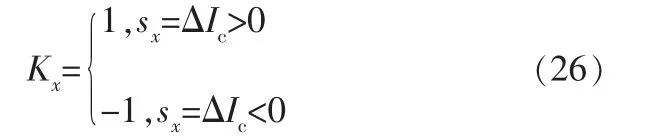
其中,sx为控制曲面。
从式(26)可以明显看出,没有电流跟踪误差ΔIc=0时的等效控制,即只有当ΔIc不为0时滑模变结构控制器才被激活,控制器只识别切换曲面的两侧。 所以这种控制不能实现对给定无差异的跟踪[6]。
为了弥补递推积分控制算法响应慢的不足,引入滑模变结构控制,如图2所示,将PI控制器的输出W(uc(K))作为滑模变结构控制的一个输入量,当电流跟踪误差ΔIc较大时,滑模变结构控制起主要作用,此时ΔIc降低较快,当电流跟踪误差ΔIc较小时,递推积分控制起主要作用,此时可以保证逆变器输出的电流实时跟踪指令电流。
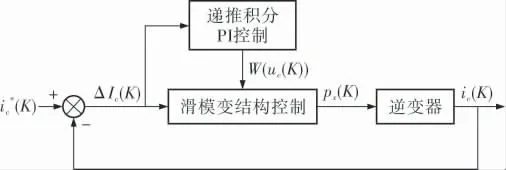
图2 复合变结构控制系统结构框图
新的滑模变结构控制的控制率px(K)为:
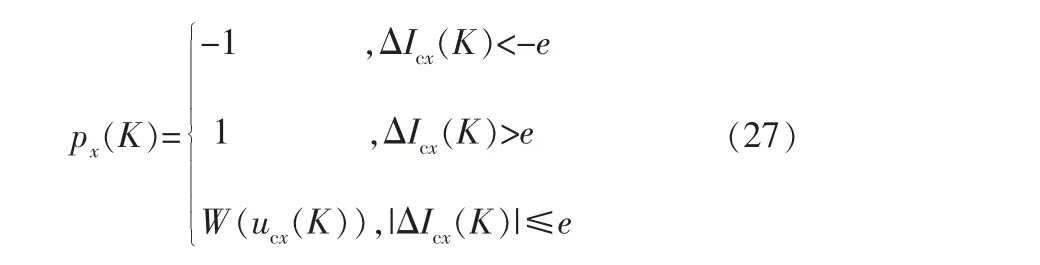
其中,下角x代表采样点数。
3 实验验证及分析
为了验证笔者提出的控制策略的可行性,利用Matlab/Simulink仿真软件, 分别搭建滑模变结构控制(图3)和递推积分滑模变结构复合控制模型(图4)进行仿真实验,谐波源是两个二极管整流桥负载,0.08 s第2个整流桥投入, 负载动态变化, 注入电网的谐波特性发生变化,APF电路在0.04 s接入,观察APF的滤波效果。
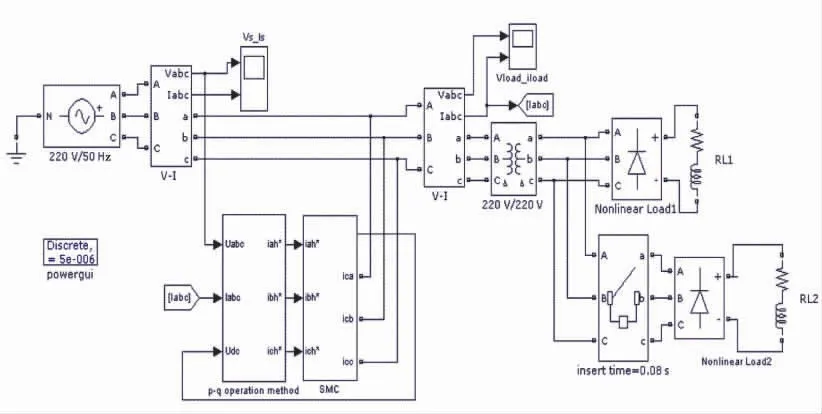
图3 控制系统仿真模型
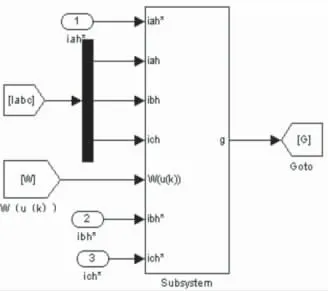
图4 复合控制部分模型
以A相为例,从图5可以看出,补偿前负载电流含有大量谐波, 谐波次数主要是5、7、11、13等次, 使得负载电流发生了畸变,THD=24.72%,远超过低压(≤1 kV)电网THD<5%的标准。如图6所示, 采用滑模变结构控制补偿后A相电流谐波总畸变率THD=3.55%,电流畸变率大幅降低。 如图7所示,采用递推积分滑模变结构复合控制补偿后A相电流THD=2.55%, 比单独的滑模变结构控制电流畸变率降低了1%,补偿后A相电源电流波形如图8所示。
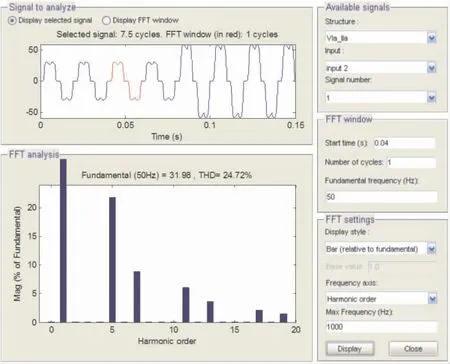
图5 A相负载电流谐波图
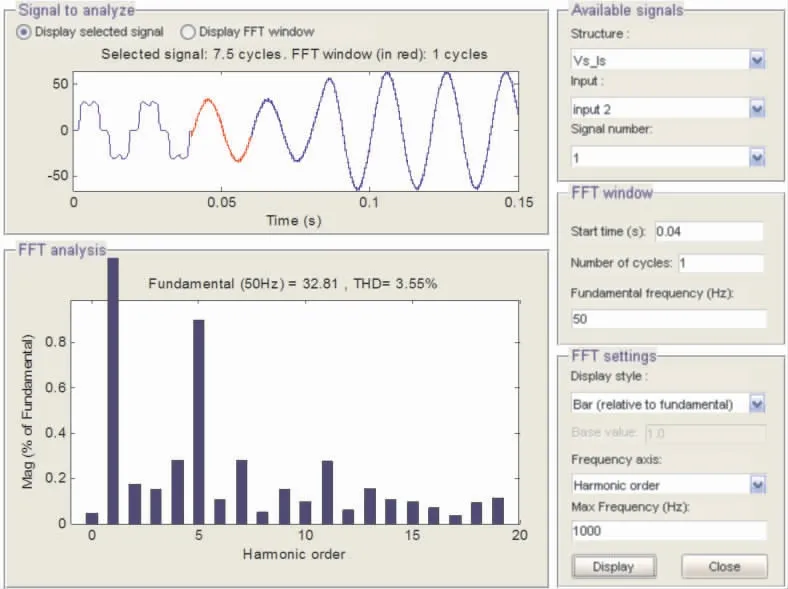
图6 滑模变结构控制补偿后A相电源电流的谐波分析
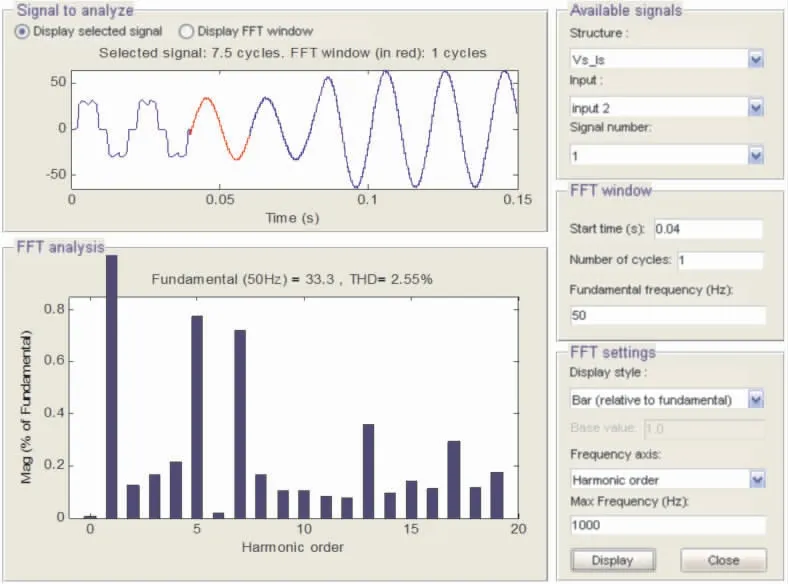
图7 递推积分PI与滑模变结构复合控制电源A相电流谐波分析
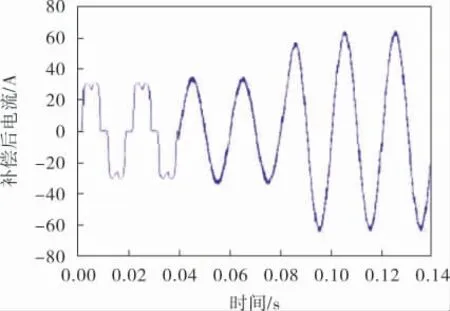
图8 补偿后A相电源电流波形
对比图9、10的曲线可以发现, 递推积分滑模变结构复合控制比传统滑模控制的电流跟踪误差明显减小,对APF来说提高了直流侧电压的利用率。
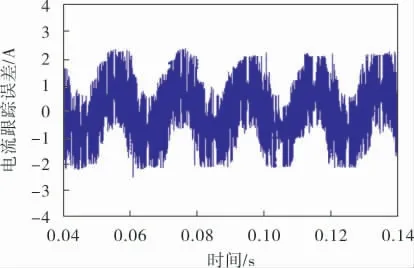
图9 滑模变结构控制电流跟踪误差
4 结束语
笔者提出一种基于离散信号迭代运算理论的递推积分PI控制算法,对于周期性的被控量它能够实现无静差跟踪,滑模变结构控制具有响应速度快等优点。 笔者将两种控制算法结合设计出多重滑模变结构控制器,将控制策略应用在有源电力滤波器中,仿真结果表明,多重滑模变结构控制电流跟踪性能好, 有效降低了谐波含量,本方法也为研究消除滑模变结构控制存在稳态误差提供了借鉴。

