物理空间中无光标反馈的指向端点分布模型研究

孟曙光 殷继彬

（昆明理工大学信息工程与自动化学院）

万物互联的时代，人与万物的互联互通将使世界充满无限活力。 计算机借助传感器对周围环境的感知和控制， 可以帮助人们提前进行决策。智能家居的指向交互技术蓬勃发展，大量厂商提出基于指向交互的技术，比如小米提出的一指连技术，OPPO的一键连技术，苹果、三星等公司均对该技术进行布局。 然而，通过指向端点进行选择指向，对不同距离的物体精准选择仍然是一项困难的任务。 在现实生活中，人们在操纵目标物体（例如遥控电视、空调）之前会调整指向方向，使之与目标物体的方向相匹配，因此需要通过判别用户意图来预测要选择的对象［1］。 由于用户进行指向选择时，手部没有物理支撑［2］，机体的生理性震颤［3，4］会进一步阻碍目标的准确选择［2］。 当目标远离用户时，指向技术通常会受到严重影响［5］。在过去的几十年里， 空间输入设备有了巨大的进步，操纵任务通常依赖于选择任务。 因此，对于物理空间中高效、准确和轻松的新式指向目标选择交互技术仍然具有挑战性。

目前， 指向目标选择技术的研究主要针对AR、VR领域，基于控制器的指向技术通常利用手持式设备向场景发射激光指针，选择与光线相交的第1个物体［5，6］。 因这种指向选择技术简单、高效，故开展了很多基于该技术的研究。指向选择和建立交互是指向目标选择技术中的基本问题，对人类交互体验有着重大影响［7］。 而物理空间的指向交互无法像虚拟空间一样借助光标、 激光射线及虚拟手等方式实现指向反馈， 解决物理空间中无光标反馈的指向交互是当前亟待解决的问题。通过对指向选择任务的端点分布进行分析， 建立基于指向的端点分布模型， 对用户指向意图进行判断，帮助用户选择预期的目标，可以较好地解决物理空间中无光标反馈指向交互存在的问题。 因此， 建立基于物理空间无光标反馈的指向端点分布模型具有较大的研究意义。

1 指向端点分布模型

端点指用户使用指向性交互设备进行交互操作时，手持指向设备的指向射线对于目标操控设备所处平面的交叉点的坐标。 而指向端点总落在目标设备周围，呈散点状分布。 对物理空间中无光标反馈的指向目标选择任务进行分析，指向端点坐标呈现x轴与y轴的二维分布，同时在x、y轴上分别呈现正态分布，即端点以二维正态分布为基础，二维正态分布的概率密度函数f（x，y）为：

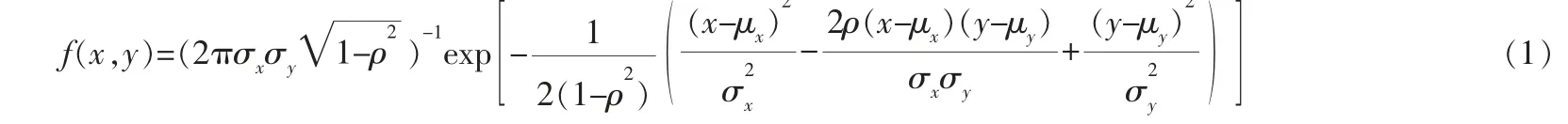
其中，ρ是x和y之间的相关性系数；μx和μy是x和y的期望值；σx和σy是x和y分布的标准差。

而笔者更关注于目标距离D对端点分布的二维正态模型中期望μ和协方差矩阵Σ这两个参数的影响：

指向任务是通过控制手臂来操控手持设备指向目标。 点击确认阶段的任务是当指向阶段任务完成后，保持手臂平稳，进行点击确认，发送交互指令。 由于指向阶段，每次指向任务的指向方位会发生不同程度倾斜，指向端点并非恰好与目标点重合，而是落在目标点周围，从而产生选择误差，同时身体会伴随生理性颤动，导致每次指向任务的端点会处于不同的位置，而上述问题会使端点呈现二维正态分布。

由于视觉误差会使主观意识上的指向目标与实际指向方位发生偏差，视线方向位于指向方向上方。 由于方向不一致，导致指向端点向目标点上方偏移，即指向阶段会因为视觉误差使得实际端点与主观端点产生偏差，从而影响端点分布模型的期望μ。

在进行指向性交互操作时，人们通常与目标之间处在不同的距离， 即目标距离D会影响指向阶段的操作精度。随着目标距离D的增长，选择误差、手臂和手部的生理性颤动对端点分布的影响被逐渐放大，即影响协方差矩阵Σ。 同理，随着目标距离D的增长， 其与视觉误差交互作用对端点分布模型的期望μ的偏移量也会增加。 综上分析，得到物理空间中无光标反馈的端点分布模型：其中，a、b、c、d、e、f、g、h为根据经验确定的常数，需通过实验验证和分析确定。

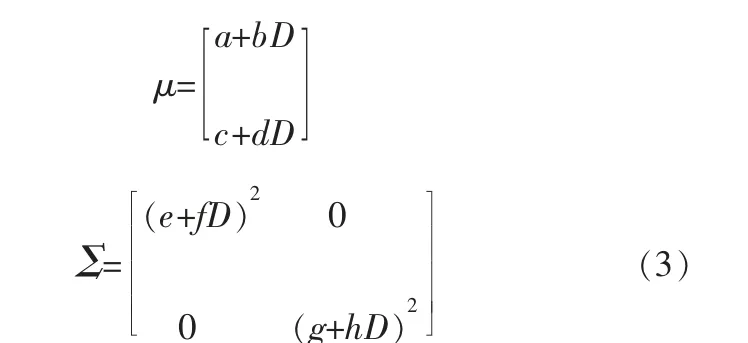
2 实验验证及分析

2.1 实验环境

本研究中的实验设备主要有： 计算机1台、Optitrack动作捕捉设备1套、投影仪1台。 Optitrack动作捕捉检测设备用于提供实验所需环境并自动记录实验中的时间、各标记点的三维坐标等实验数据。 计算机与Optitrack动作捕捉设备的性能参数和运行的软件环境见表1。

表1 实验设备的性能参数和运行的软件环境

在实验设计开始前，需要将目标大小设置为最适宜的尺寸，并对实验参与者有一个共同的要求。 根据菲兹定律中的一个默认假设：“尽可能快速地移动，并达到准确的位置”，以此满足实验数据的可靠性［8］。

实验自变量为：参与者与目标的距离D（600、1 200、1 800、2 400、3 000 mm）。该实验的设计总共得出：15名参与者×5组实验×50次选择任务=3750组数据。

将目标交互设备使用标记点进行模拟并用三角架进行固定，参与者站立在与三角架的不同距离处，使用惯用手进行指向目标选择。 当认为选中目标时，进行点击确认。 实验设计了一个指向器，方便采集和分析指向信息。 实验时，要求参与者采用最舒服的姿态握持指向器和鼠标，自然地尽快指向目标并点击确认，实验环境如图1所示。 Optitrack捕捉指向器记录前后标记点和目标标记点坐标，计算指向端点坐标。 完成一组实验后，将采集到的数据以.xlsx格式文件输出保存。

图1 实验环境

2.2 实验结果及分析

使用Origin和SPSS软件对实验数据进行了重复测量方差分析（置信度α=0.05）。 当数据违反球形假设时， 使用Greenhouse-Geisser方法校正，并对组件数据进行事后检验两两比较。

2.2.1 正态性检验

使用Origin 2021b软件对不同目标距离上的5组数据进行正态性检验，通过Kolmogorov-Smirnov假设以确定x轴和y轴上的正态分布，α=0.05。并通过Origin 2021b对x、y的相关性进行Pearson相关性检验， 通常认为相关系数在-0.3～0.3是微相关或不相关。 分析结果见表2。

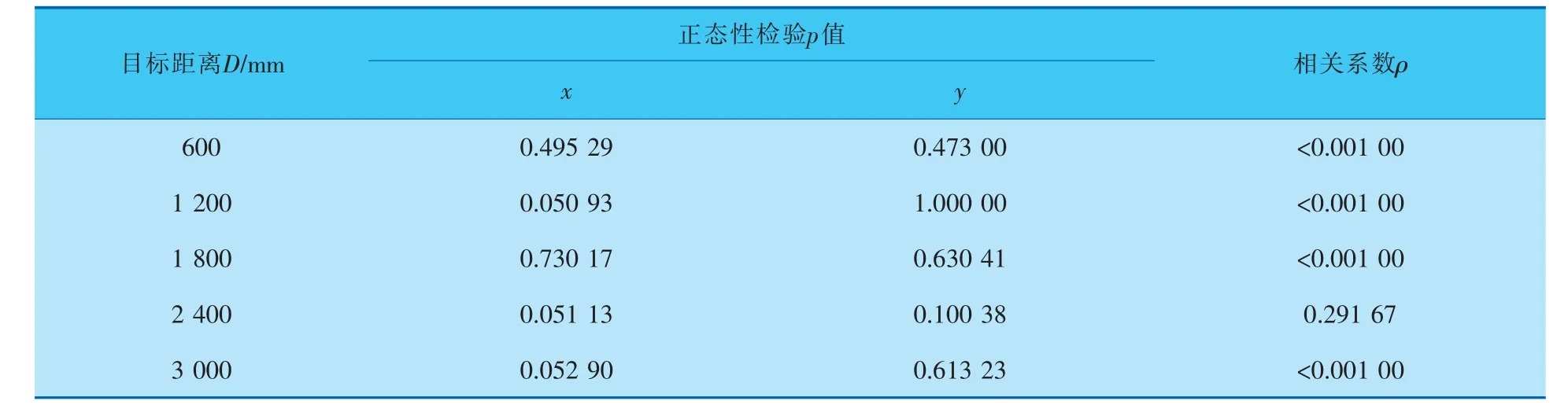
表2 端点分布正态性、相关性分析结果

由实验数据可知：各组数据均大于0.05，所以拒绝原假设，不能排除正态性，端点的x、y均符合正态分布。 各组数据的相关系数均处在-0.3～0.3之间，特别对于600、1 200、1 800、3 000 mm这4组数据，其相关系数ρ几乎趋近于0，因此认为各组数据的x、y之间相互独立。

正态性检验结果表明，所有端点集均通过了x轴和y轴上的正态性检验， 即x轴和y轴坐标服从正态分布， 同时实验数据证明了x与y相对独立，即x与y其中一个的出现不会影响另外一个的出现率。 综上所述，基于指向的端点分布模型服从二维正态分布。

2.2.2 目标距离对模型的影响

使用SPSS软件对不同目标距离上的5组数据进行了重复测量方差分析ANOVA（α=0.05）。

在对x轴坐标的重复测量方差分析中， 目标距离在Mauchly检验上χ2（9）=456.345，p＜0.001，因变量不满足球形假设。 经Greenhouse-Geisser方法校正（F2.847，1338.279=61.749，p＜0.01），表明不同目标距离对指向目标选择任务的端点分布的x轴方向具有显著性影响。 对组间数据差异进行成对比较分析，结果见表3。

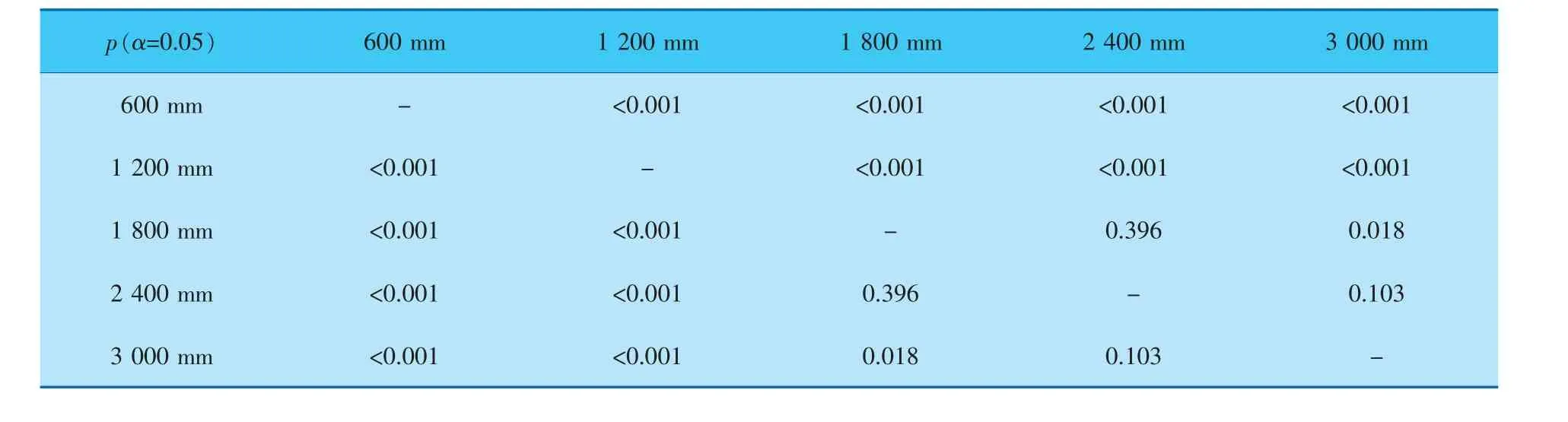
表3 不同目标距离x坐标组间差异比较

由表3可知， 除了1 800 mm与2 400 mm （p=0.396）、2 400与3 000 mm（p=0.103），其余各组间的x坐标p值均小于0.05。由此认为目标距离对x坐标存在显著影响。

对自变量目标距离D的5组不同数据，能够计算各组期望μx和标准差σx，通过Origin对其进行线性拟合，结果如图2所示。

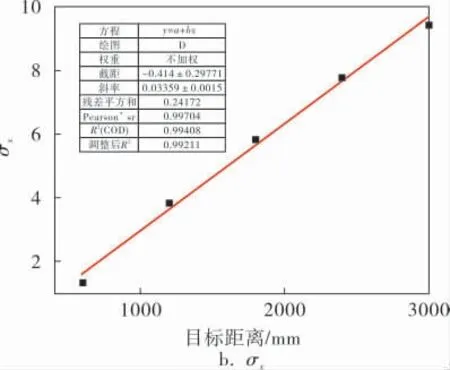
图2 5组不同目标距离D端点分布的μx和σx拟合

在对期望μx的拟合中得到下式：

调整后拟合优度R2为0.786。

在对标准差σx的拟合中得到下式：

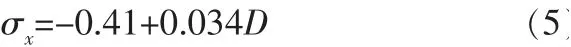
调整后拟合优度R2为0.992。

对5组不同目标距离的端点分布的期望μx、标准差σx进行的回归分析表明，这些因素与因变量目标距离D之间存在很强的线性关系。

在对y轴坐标的重复测量方差分析中， 目标距离在Mauchly检验上χ2（9）=761.631，p＜0.001，因变量不满足球形假设。 在分析中使用了Greenhouse-Geisser方法校正 （F2.69，1353.131=470.201，p＜0.01），表明不同目标距离对指向目标选择任务的端点分布的y轴方向具有显著性影响。 对组间数据差异进行成对比较分析，结果见表4。

表4 不同目标距离y坐标组间差异性比较

由表4可知，5个不同目标距离的y坐标组间p值均小于0.001，满足小于0.05的要求。 由此认为目标距离对y坐标存在极为显著影响。

对自变量目标距离D的5组不同数据，能够计算各组期望μy和标准差σy，通过Origin对其进行线性拟合，结果如图3所示。

图3 5组不同目标距离D端点分布的μy和σy拟合

调整后拟合优度R2为0.985。

对5组不同目标距离的端点分布的期望μy、标准差σy进行回归分析表明，这些因素与因变量目标距离D之间存在很强的线性关系。

通过分析因变量目标距离对x、y的影响，可以看出目标距离对x、y具有显著影响，x、y与目标距离呈现正相关的线性关系。

通过目标距离对模型的影响分析，表明目标距离D是μx、μy、σx和σy这4个参数的主要影响因素。 线性回归还揭示了目标距离D对μx、μy、σx和σy这4个变量的强线性关系。 观察式（4）和式（6）的斜率发现，式（6）中的斜率近10倍于式（4），所以由于视觉误差的存在，μy的偏移量明显大于μx的偏移量。 这是由于视线方向与指向器方向并不处于同一方位上，从而导致指向方向向视线方向进行偏移。

2.3 实验结论

通过实验分析，无反馈目标指向任务的端点分布服从二维正态分布， 且x轴与y轴相对独立。无反馈目标指向任务的端点分布由目标距离、视觉误差及手部颤动等因素决定，端点分布模型的均值和标准差与目标距离之间有强关联关系，均值和标准差随着目标距离的增长呈现正相关的增长。

通过目标距离对模型的影响分析，并对期望μx、μy和标准差σx、σy进行线性拟合，得到线性拟合公式（式（3））。 对式（3）中的经验常数a、b、c、d、e、f、g、h进行代换，得到物理空间中无光标反馈的指向端点分布模型：

指向端点分布模型对期望μx、μy和标准差σx、σy调 整 后 的 拟 合 优 度R2分 别 为0.786、0.992、0.984、0.985，可以很好地对物理空间无光标反馈的指向端点分布进行描述。

3 结束语

笔者提出了面向物理空间的无光标指向性选择任务的端点分布模型。 该模型探索了目标距离、视觉误差、手部颤动等因素对指向目标端点分布的影响，从而预测指向目标选择的端点分布区域。 模型的研究是基于实验中收集的数据进行的。 总体而言，端点分布模型对物理空间中指向任务的端点分布有较高的拟合程度，可以较好地预测用户指向意图，提升物理空间中指向选择任务的交互体验。