分数阶PMSM混沌系统的柔性同步控制研究

王军光 郭浩轩

（1.国能榆林化工有限公司；2.东北石油大学电气信息工程学院）

永磁同步电动机（PMSM）系统具有良好的动态特性，具有高效率、高性价比、高可靠性等特性［1］，适用于中低端的工业应用功率范围，被广泛应用于石油石化等领域［2～4］。 分数阶PMSM系统由于在系统模型中引入了分数阶微积分理论，优化了系统模型，因而能够更好地表现永磁同步电机的动态特性［5］。

PMSM系统是含有多变量耦合的非线性系统。 对非线性动力系统的动态特性进一步研究发现，PMSM的状态变量存在混沌现象［6］。文献［7］讨论了PMSM系统混沌现象的存在， 发现在一定条件下，PMSM系统状态变量呈现杂乱无章的变化，但相图中存在吸引子。 PMSM系统的混沌现象会影响电机工作的稳定性，为了消除此种不稳定特性，需要对其混沌状态进一步分析和研究。

近年来， 分数阶PMSM混沌系统同步控制被广泛研究。 文献［8］针对不确定参数分数阶PMSM系统同步控制， 提出了一种新分数阶控制方法，实现了初值不同参数不确定的两个分数阶PMSM系统的同步控制。 文献［9］研究了分数阶PMSM系统中混沌现象存在的条件，并通过设计控制器实现了分数阶PMSM系统的同步控制。 文献［10］利用分数阶滑模变结构控制方法，实现了两种不同PMSM系统的同步控制。 然而，目前对于柔性变结构控制策略的研究则较少。

笔者利用柔性变结构控制策略实现同步控制， 对两个分数阶PMSM混沌系统的稳定性进行理论分析， 最后通过常见的分数阶PMSM系统数值仿真进行验证。

1 问题描述

分数阶PMSM混沌系统如下［11］：

当系统初始状态为x（0）=［1，1，0.1］时，系统呈现出如图1所示的混沌现象。

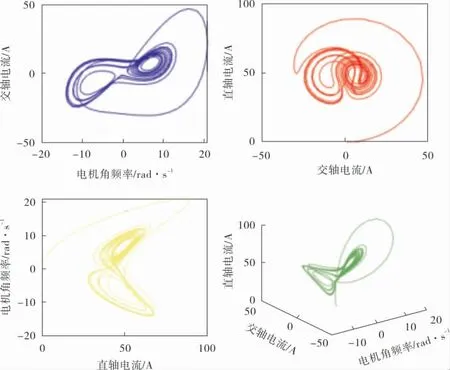
图1 分数阶PMSM系统初始状态下的混沌现象

对上述结构相同初值不同的分数阶PMSM混沌系统进行同步控制， 可将系统简化为如下形式：

2 同步控制器设计

为实现两初值不同系统的同步控制，采用分数阶Lyapunov理论，设计柔性变结构同步控制器。由式（3）得：

其 中，ui=H（p，e），H 为 光 滑 函 数 并 且 满 足Lipschitz条件，p=［p1，p2，p3］为控制器参数；aij为系统参数。 为了设计柔性控制器，采用分数阶微积分的方法确定选择参数pi，则选择参数pi连续变化时，控制器也会变化，避免出现抖振情况。 其中选择参数取：

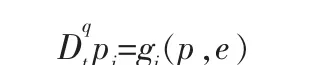
定义1 在所设计控制器ui的作用下， 系统（4） 是Lyapunov稳定的。 即控制器实现两分数阶PMSM系统的实时跟踪。

证明 根据分数阶PMSM同步系统选取Lyapunov函数：

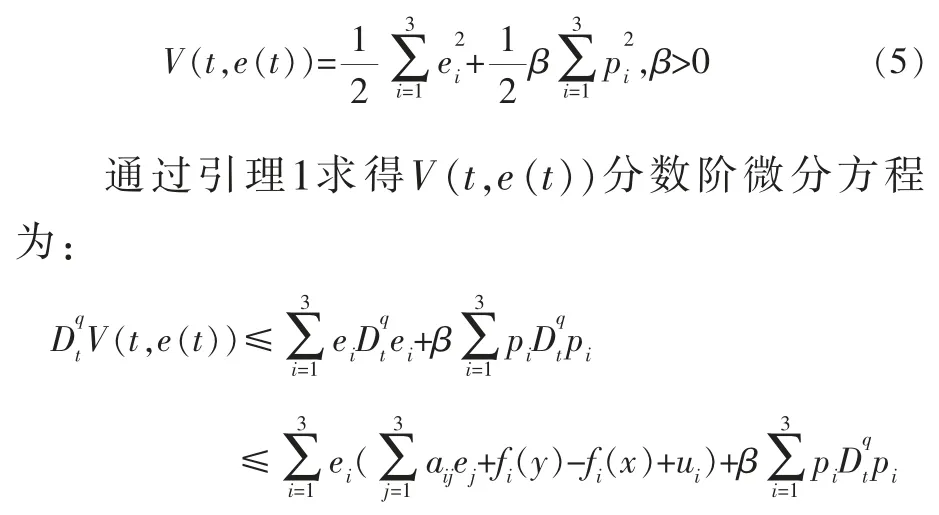
由分数阶Lyapunov稳定性理论判定该系统是渐近稳定的，证明从任意初始条件出发的误差系统（3）将稳定在平衡点。 所设计的控制器（6）实现了系统（2）与系统（1）状态变量之间的同步控制。

3 数值仿真

对三维分数阶PMSM混沌系统进行数值模拟仿真，以验证该方法对两永磁同步电机混沌系统同步控制的效果。

驱动系统为：

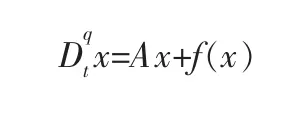
分数阶阶次q=0.98。 两系统的状态变量初始值x（0）=［1，1，0.1］，y（0）=［0.01，0.01，0.01］。

如图2所示，当控制器u无输出时，系统状态误差在10 s内不收敛。

图2 无控制器作用时系统状态误差曲线

为使系统误差收敛并趋于稳定，加入柔性控制器ui=-kiei-piliei，选取k=［2，2，2］。

为体现柔性控制器反应迅速的优越性，先设置控制器中的l=［0，0，0］，即控制器为：

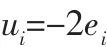
得到当控制器为比例控制器时的系统状态误差曲线如图3所示， 可以看出此时误差曲线收敛速度较慢。

图3 比例控制器下系统状态误差曲线

为缩短两分数阶PMSM系统同步的时间，利用柔性变结构控制器（6）对该系统进行控制。 为简化仿真，选取l=［1，1，1］，φ（p，e）=1，β=1，使选择参数pi在一定范围内。 通过数值仿真得出柔性控制器作用下系统误差曲线如图4所示， 选择参数pi如图5所示。从图4中可以看出，柔性变结构控制使得系统误差更快地收敛至平衡状态，具有更短的收敛时间。 图5中最初2 s需要控制器较大的调节能力， 此时选择参数较大；2 s后系统趋于稳定，控制器输出会干扰系统稳定，故选择参数逐渐衰减至0，从而具有更快的稳定时间。

图4 柔性控制器下状态误差曲线

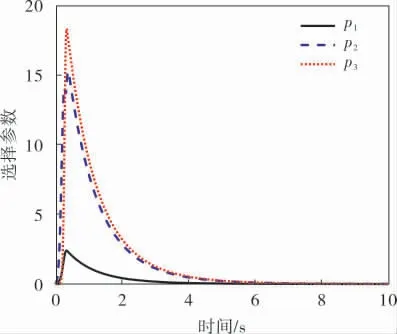
图5 选择参数变化曲线

为进一步验证柔性控制器对系统误差的影响，仿真中对柔性变结构控制器的加入时间加以设定，在仿真开始2 s后加入控制器，结果如图6所示。可以看出，仿真的前2 s误差曲线不稳定、波动大，在2 s后加入柔性控制器后，系统状态误差逐渐趋于稳定，收敛速度较快。 仿真结果表明，两分数阶PMSM系统在任意初始条件下， 柔性变结构控制器使得同步误差状态渐近稳定，两系统状态变量实现了同步。

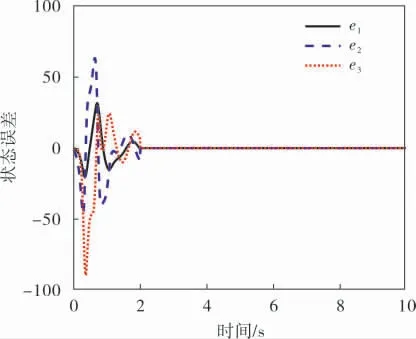
图6 2 s后加入柔性控制器后的误差曲线

4 结束语

笔者设计了一种柔性变结构控制器，实现了两不同初值分数阶PMSM混沌系统的同步控制。通过柔性变结构实现对两系统同步时间的改变，并通过分数阶稳定性理论判定了误差系统的稳定性。 控制器缩短了两分数阶PMSM系统状态变量的跟踪时间。Matlab仿真验证了在分数阶PMSM系统同步控制中， 该控制器缩短收敛时间的优点。