基于WGAN的多孔材料三维重建

张傲克, 钱宇航, 齐 红

(吉林大学 计算机科学与技术学院, 长春 130012)

0 引 言

多孔材料在工程应用中具有重要价值[1-2]。根据“结构决定性质, 性质决定用途”原则, 如何采用适当的方法探究其内在联系是人们关注的重点。目前, 通过计算机断层扫描技术[3]可直接获取3D图像, 但该方法存在高成本、 分辨率低等缺点。 已有的三维重建方法, 包括基于优化的方法[4-5]、 直接取样法[6-7]和多点统计法[8-9]等, 对三维重建问题计算时间复杂度、 空间复杂度和准确率仍然是衡量模型性能的重要标准, 而上述方法在其不同方面均存在一定的缺陷。但通过这些算法可知, 提取一个图像的形态学特征, 并利用该潜在空间中的向量进行三维重建是解决该问题的有效手段之一。笔者以Berea砂岩和Beadpack为数据集, 将WGAN(Wasserstein Generative Adversarial Networks)改造为用于处理三维重建问题的深度学习模型, 通过对相关评价标准的测试得知该深度学习模型具有较高准确性与较低时间复杂性等特点, 并具有较好的泛化能力。

1 Wasserstein GAN

1.1 GAN

在传统的机器学习算法中, 通常仅考虑现有的数据模式, 而无法生成新的事物。Goodfellow等[10]提出的生成对抗网络是目前非常流行的无监督学习方法之一, 该方法通过学习数据的隐式分布生成新的事物, 并且具有极好的效果[11]。在该深度学习模型中使用一个生成器与一个判别器通过相互博弈实现分布近似。其中, 生成器通过给定输入生成需要的结果, 而判别器则用于判断所输入内容是否为真, 生成器和判别器进行以下最小-最大(min-max)博弈

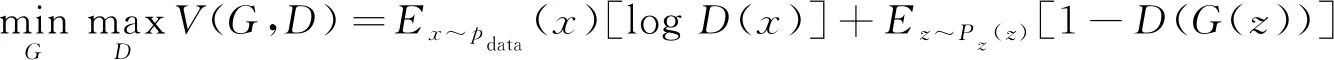
(1)

图1 GAN训练流程Fig.1 The training process of GAN

通过式(1)可知, 在训练过程中首先固定生成器, 并通过训练使判别器达到最优, 即让判别器输入生成数据时判别为假, 输入真实数据时判别为真。再固定判别器, 训练生成器使其达到最优, 即让判别器在输入生成数据时判别为真。重复上述过程, 进行迭代训练达到或接近纳什均衡点, 此时GAN处于收敛状态。

图1为GAN的训练流程。但GAN存在收敛速度慢、 模式崩溃和过度泛化等问题[12], 而Wasserstein GAN则可在一定程度上解决上述问题。

1.2 Wasserstein距离

对式(1)进一步分析可得

V(G,D*)=2J(pr(x)‖pg(x))-2log 2

(2)

而J散度又存在饱和区间, 同时根据“当Pr与P-g的支撑集是高维空间中的低维流形时,pr与pg重叠部分测度为0的几率为1”[13]结论, 可知GAN在初始化状态下就可能出现严重问题。因此, 需要对J散度进行替代。

最优输运起源于Monge问题, 并由Kantorovich通过对偶理论加以发展, 进而提出了Kantorovich-Rubinstein距离等重要概念[14]。最优输运的相关理论在流体力学、 生物医学和人工智能等领域中有重要应用价值。其中, Wasserstein距离[15](简称W距离)是最优输运理论中的重要概念, 其代表诸多输运方法中的最小代价。W距离为

(3)

通过对W距离分析可知, 其具有交换性、 非负性和指标性, 因此解决了J散度的相关问题。并且对生成图像的概率分布, 可通过求解线性规划的对偶问题解决。最终损失函数可更新为[13]

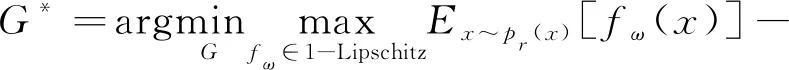
(4)

1.3 Lipschitz连续

通过式(4)可知,fω(x)需要满足k-Lipschitz连续。为满足这个条件, WGAN中使用了一种称为权重裁剪的策略。由于, 在WGAN中Lipschitz连续并不关注于梯度的具体大小, 而是要保证梯度在合理范围内。因此, 通过将fω(x)中的ω限制在[-c,c], 进而使函数的输出值控制在一定范围内, 通过这种方式保证输出值的变化在一个有限的范围内。

2 评估标准

2.1 两点相关函数

两点相关函数计算了随机距离为‖r‖的两点落在同一个相中的概率[15]。其公式为

S2(r)=P(x∈P,x+r∈P),x,r∈n

(5)

其中S2(0)是孔隙率φ, 孔隙率描述了多孔材料存储流体的能力, 并且当r→∞时,S2趋近于φ2。通常由于其各向异性, 需沿x,y,z3个笛卡尔坐标方向计算S2(r)的值, 以及其径向平均值。同时可通过函数图像获取更多信息。由文献[16]可知, 在一个各向同性的多孔材料中, 比表面积Sv与S2满足

(6)

其中比表面积的大小与物体的吸附能力有关。并通过式(5)可计算出颗粒相与多孔相中的弦长。其计算公式为[17]

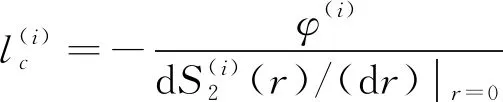
(7)

2.2 Minkowski泛函

采用Minkowski泛函对多孔材料进行数据分析是通过形态学特征刻画多孔材料特性的基本方法之一。Minkowski 泛函起源于有关凸集的理论, 积分几何中的Hadwiger理论表明可用d+1维参数描述d维的嵌入空间。因此, 对三维图像可采用4个Minkowski泛函刻画其形态学特征[17]。

式(8)是孔隙率, 表示孔隙所占体积与重建对象的总体体积之比。式(9)用于计算比表面积。式(10)是物体表面的平均曲率, 其中r1和r2是面积元dS的最小和最大曲率半径。式(11)与Euler特性密切相关, 它表示了总体曲率。但在实际计算过程中考虑Euler数, 式(11)可表示如下

χ=V-E+F-O

(12)

其中V是顶点数,E是边数,F是面数,O是对象的数量。Euler数表示了介质的连通性等性质。但由于计算工具受限, 在实际数据分析过程中没有计算表面的平均曲率。其余参数通过image J的MorphoLib J进行计算。

2.3 渗透率

渗透率[17]表示流体穿过多孔材料的能力, 高渗透性材料意味着流体更容易通过相应介质。渗透率可看做Darcy定律在多孔材料中的应用。Darcy定律表述如下

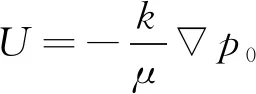
(13)

其中U是平均流体速度,p0是压力梯度,k是介质的渗透率,μ是流体的动态粘度。在计算中, 需要考虑具有一定流量的动态连通部分, 因此需要计算有效孔隙率

φeff=Vflow/V

(14)

渗透率有很多实际应用, 如从多孔岩石中提取石油, 以计算相关数据。为计算原始三维图像以及生成的三维图像中的渗透率, 可采用描述粘性不可压缩流体动量守恒的运动方程, 即Navier-Stokes方程, 关系式为

μΔv=p

(15)

(16)

2.4 后期图像处理

根据Nyquist准则可知, 对一个无噪声低通信道, 最高码元传输速率B满足关系

B=2W

(17)

图2 CT图像的局部放大结果Fig.2 The local magnification result of CT image

其中W是带宽。在图形学中, 经常遇到锯齿、 摩尔纹和车轮效应等走样现象。走样是指低频采样造成的信息失真。由于CT扫描过程存在走样现象(见图2), 因此考虑相应方法对图像进行后期处理。由于已经完成采样, 产生了频谱的混叠, 所以只能通过滤波等操作处理相应的图像, 使生成的岩石表面更加平滑、 清晰。

采用opencv[19]中的相应函数对图像进行处理, 包括中值滤波、 双边滤波和线性滤波。不同的滤波器对图像平滑的方式不同, 例如中值滤波是一种非线性滤波器, 它根据邻域窗口中像素值的中值确定该点处的像素值。通过对每种方法进行尝试, 最终根据实际情况选择合适的处理结果作为最终的生成图像。

3 基于WGAN的三维重建

3.1 网络架构

判别器中将三维卷积神经网络与三维批处理层作为一个模块, 批处理层用于加快神经网络的收敛速度同时提高稳定性。除最后一个模块外三维卷积神经网络中卷积核的大小为(4,4,4), 步长为(2,2,2), 并以(1,1,1)的大小进行填充, 以保留边界信息。同时, 其余模块中均有线性整流函数作为激活函数, 以引入更多的非线性因素增强模型的拟合能力。在最后一个模块中, 不使用激活函数与批处理层, 并且步长为(1,1,1),不进行填充, 卷积核的大小仍为(4,4,4)。对卷积神经网络和批处理层, 其超参数均采用默认值。最终将1×64×64像素的图像转换为1×1×1的距离值。判别器的示意图以及相应的输入输出通道数如图3所示。

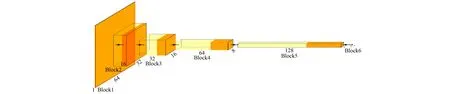
图3 判别器示意图Fig.3 The schematic diagram of the discriminator

由于输入数据维数为4。因此, 用每层网络的宽度表示其通道数, 边长表示三维图像的边长。生成器除最后一个模块外将三维反卷积神经网络与三维批处理层作为一个模块, 三维反卷积神经网络中卷积核的大小均为(4,4,4), 步长为(2,2,2), 以(1,1,1)的大小进行填充, 并且每个模块中均使用线性整流函数。其中在第1个模块中, 仅有一层三维反卷积神经网络, 卷积核大小仍为(4,4,4), 但步长为(1,1,1), 并且不进行任何填充。最后, 通过双曲正切函数处理输出结果。反卷积神经网络和批处理层均采用默认超参数值。生成器的示意图以及输入输出通道数如图4所示。由于输入数据维数为4。因此, 将每层网络的宽度表示其通道数, 边长表示三维图像的边长。

图4 生成器示意图Fig.4 The schematic diagram of the generator

根据Arjovsky等[13]提出的权重裁剪简单地实现Lipschitz连续, 并将相应的参数取为±0.01。但在实际训练中, 应将权重值取为尽可能大的值如±1 000 000, 否则将出现训练失败等情况。同时, 自适应学习率算法应采用非动量算法, 一般使用RMSProp, 该方法已被证明具有良好的效果[20]并得到广泛应用。

4 基本流程

4.1 Berea砂岩

图5所示为Berea砂岩, 是一种浅灰色至浅黄色, 颗粒大小为细粒到中粒的砂岩。Berea砂岩通常用于建筑材料, 同时也是石油和天然气的重要来源。

采用的CT扫描图像来自于文献[18], 该图像的原始大小为400×400×400像素, 以32为步长, 并将原始图像分割成大小为64×64×64像素的子图像。将得到的三维图像作为真实数据在训练中使用。

4.2 Beadpack

Beadpack是一种由相同大小的颗粒无序堆积而成的人造岩心。笔者采用的Beadpack原始图像大小为500×500×500像素, 并将原始图像以步长32进行分割。在训练过程中, 使用子图像作为真实图像的数据集。

图5 Berea砂岩的三维图像 图6 Beadpack三维图像 Fig.5 Three dimensional image of Berea sandstone Fig.6 Beadpack 3D image

首先通过使用满足高斯正态分布并且通道数为512的随机噪声, 固定预先经过初始化的生成器, 并生成相应数据。然后将生成数据与真实数据分别输入判别器, 并计算相应的损失函数值, 通过误差逆传播算法更新判别器中的相应权重。参数值的更新公式如下

ωk+1=ωk-αf(ωk)

(18)

完成该轮对判别器的训练。固定判别器, 对判别器输入生成数据并计算相应的损失函数, 通过误差逆传播算法更新生成器的相应参(见图7)。

图7 训练流程示意图Fig.7 The schematic diagram of the training process

图8为生成图像与迭代次数关系。由图8可知, 在训练初期, 无法观察到具有孔隙结构的图像, 在立方体表面只有模糊的斑点。但在迭代5 000次时, 已经能看见相对清晰的孔隙。而在10 000次～20 000次之间, 训练效果趋于稳定。但当训练次数继续增加达到40 000次左右时, 孔隙数量有一定的减少。

图8 生成图像与迭代次数关系Fig.8 Generate a graph of the relationship between the image and the number of iterations

4.3 数据分析

通过式(5)可计算出重建图像的径向平均两点相关函数值与沿着x,y,z3个方向的归一化两点相关函数值(见图9)。

图9 Berea砂岩生成图像的径向平均两点相关函数值与3个笛卡尔坐标方向的两点相关函数值Fig.9 The radial average two-point correlation function value of the image generated by Berea sandstone and the two-point correlation function value of three Cartesian coordinate directions

由图9可知, 基于WGAN的模型在孔隙率、 比表面积和函数拟合等方面均具有较好的效果。而在图10中, 笔者采用箱线图对原始图像与合成图像进行分析。箱线图的上下两条线表示最大值和最小值, 而长方形的上下两边分别表示上四分位数和下四分位数, 即数据经过排序后处于25%和75%的位置。方格中间的虚线表示数据的中位数。

通过结果可看出, 由该模所生成的图像具有与原始图像类似的拓扑性质, 即具有相似的连通性。图11给出了基于WGAN的三维重建图形的渗透率。从图11可看出, 生成图像的有效孔隙率与渗透率的关系表现出的相关性与原始图形类似, 并且坐标点的分布也比较接近。

图10 原始图像与生成图像的Minkowski functional比较结果Fig.10 Comparison results of Minkowski functional between original image and generated image

图11 原始图像与生成图像的渗透率比较Fig.11 Comparison of permeability between original image and generated image

为验证基于WGAN的三维重建模型能广泛适用于不同数据集, 采用Beadpack进行测试(见图12)。通过对其归一化两点相关函数的对比图像可知, 其在笛卡尔坐标方向和径向方向均具有较好的拟合效果。从而进一步表明了该模型的泛化能力。

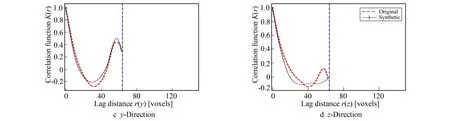
图12 Beadpack生成图像径向平均两点相关函数值与3个笛卡尔坐标方向的两点相关函数值Fig.12 Beadpack generates the radial radial average two-point correlation function value of the image and the two-point correlation function value in three Cartesian coordinate directions

4.4 后期处理

使用opencv中的中值滤波、 双边滤波和线性滤波进行比较, 最终选用中值滤波对图像进行处理。从图13中可看出, 图像的清晰度明显提高, 岩石表面更加连续、 光滑。

图13 原始重建图像和经过平滑处理后的结果Fig.13 The original reconstructed image and the result of smoothing

5 结 语

基于WGAN的三维重建模型具有较低时间复杂度。基于随机数的三维重建模型在NVDIA 3060上完成对berea砂岩和Beadpack图像的84 000次迭代仅需3.5～4 h左右。并且在1 h左右即可观察到明显效果。当训练完成后, 便可在秒级时间单位下完成三维重建, 同时通过训练得到的生成模型可存储并重复利用, 而传统方法则需要数小时完成三维重建, 并且这种通过显式分布进行学习的方法的时间复杂度随着图像的体素的增多而变大, 因此基于深度学习的模型在效率上具有明显优势。同时根据相应的性能评估标准可知, 生成图像与真实图像有较好的拟合效果。

通过对实验结果进行分析可知, 该模型仍存在以下不足: 1) 该模型可能会出现模式崩塌等常见问题, 从而导致生成图像的单一性; 2) 由几何的相应知识可知, 在整个过程中使用单张二维图像进行训练会造成信息的缺失, 从而导致生成图像不能无限接近于真实图像。因此, 通过采用更多数目的非平行图像可能会有更好的效果。

基于WGAN的三维重建模型相关参数并未进行精细调控, 例如在训练过程中可实时关注损失函数的变化情况, 通过人工改变学习率的方法提升训练效果。同时文中所示的权重截断超参数的范围为有效范围, 但实际范围可以进一步缩小。网络中的参数与网络层数量可以得到进一步地调整与缩减, 在保证高性能的同时, 能提高训练速度, 并减小空间复杂度。另外, 批尺寸大小与图像的大小也是值得考虑的因素, 通过找到相应参数的最优取值, 能加快训练速度, 提高内存利用率, 并优化训练效果。并且, 传统方法与深度学习方法相结合也是值得考虑的方向之一。可以考虑采用模拟退火算法对重建结果进行再重建, 由于通过深度学习方法可在低时间复杂度的情况下实现较高准确率的三维重建, 因此可以结合高效率的传统三维重建算法进行优化, 以实现准确率与效率的权衡。