便携式瞬变电磁系统探测未爆弹反演算法优化

李庆振, 张 爽, 陈曙东

(吉林大学 电子科学与工程学院, 长春 130012)

0 引 言

未爆弹(UXO: UneXploded Ordnance)是指战争结束后在交战区域遗留的未爆炸弹, 其将给战后区域重建和当地经济发展带来很大的安全隐患[1]。为消除未爆弹隐藏的威胁, 人们采取了多种方法探测和清理未爆弹, 其中瞬变电磁法(TEM: Transient Electromagnetic Method)由于其具有较高的抗干扰性和较低的虚警率, 得到了快速发展[2-3]。

便携式瞬变电磁系统轻便、 易于携带, 适用于山地、 丛林等其他中大型探测系统难以到达的地域, 搜寻未爆弹的过程分为探测、 反演和分类3步[4-5]。首先通过探测获取目标的电磁响应, 笔者选用吉林大学电磁传感技术实验室制作的便携式瞬变电磁系统[6]开展目标探测； 其次对数据进行反演, 获取目标体的位置参数和特征响应, 反演效率的高低直接影响未爆弹探测和清理的速度； 最后根据目标体的特征响应对目标进行分类和识别。

反演是基于某一正演物理模型, 应用某些方法对目标观测数据进行处理, 以得到目标的待定参数[7]。在未爆弹的多种物理模型中, 磁偶极子模型易于理解, 计算便捷[8]。笔者采用磁偶极子模型表示未爆弹电磁响应。基于磁偶极子模型反演目标体的位置参数和特征响应是非线性问题, 常用的反演方法有梯度法、 牛顿法、 遗传算法[7]和DE(Differential Evolution)算法[9-10]。笔者选用DE算法反演目标体的位置参数和特征响应, 通过逐项分析影响反演计算效率的相关因素, 采取对应措施进行优化, 提升反演计算速度。

1 便携式瞬变电磁系统与磁偶极子正演模型

1.1 瞬变电磁原理与探测系统

TEM是一种基于电磁感应原理的时间域电磁感应探测方法[11-12], 工作原理如图1所示。在发射线圈中接入以脉冲形式的发射电流, 从而在其周围激发出变化的一次场。地下有限导体在一次场作用下产生随时间衰减的涡旋电流, 涡旋电流将在周围空间中再次激发出随时间衰减的二次场。接收线圈接收二次场, 得到二次感应电压, 从而得到地下有限导体的相关信息。

瞬变电磁系统传感器结构如图2所示, 该传感器外圈为单分量发射线圈, 其内部按十字形布设了5个三分量接收线圈[6]。系统开展探测时, 发射线圈向目标区域发射一次场, 5个三分量接收线圈同时接收目标体旋涡电流产生的二次场, 形成15个独立的电压响应数据。为提高信号的信噪比, 接收机对数据进行了瞬态叠加和抽道叠加处理。瞬态叠加是将信号按周期叠加取平均, 以提高信号的信噪比； 抽道叠加是根据信号衰减速度将信号按一定的时间比例分为60段, 每段的数据取均值作为这段数据的信号值, 最后按照时间先后得到60道信噪比较高的数据[13]。

图1 瞬变电磁探测原理 图2 传感器结构 Fig.1 Principle of transient electromagnetic detection Fig.2 Sensor structure

1.2 磁偶极子正演模型

根据瞬变电磁原理, 在发射线圈发射的一次场BP激励下, 磁偶极子模型将目标体等效为一个中心重合、 两两正交的三维正交磁偶极子m, 用偶极子的磁场分布表示目标体的二次场分布, 接收线圈接收目标体产生的二次场, 获得到二次感应电压, 形成探测数据, 具体过程如图3所示。

接收线圈得到的感应电压为[6]

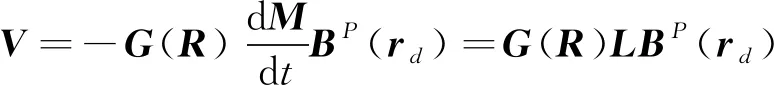
(1)

其中G(R)为格林函数, 与位置参数相关；L为特征响应矩阵, 是磁极化张量M对时间导数的负值, 轴对称物体的特征响应矩阵L为对称矩阵；BP为发射线圈产生的一次场。式(1)中L可分解为

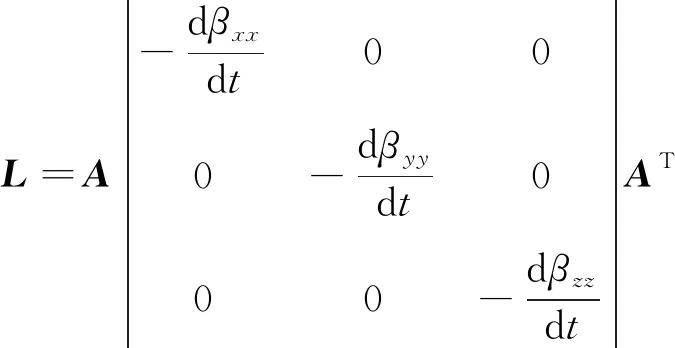
(2)

A为目标体的欧拉旋转张量, 与目标体姿态角相关；βxx、βyy、βzz为目标磁极化的主极化元素。定义l(t)为目标体的特征响应, 即主极化元素对时间的导数

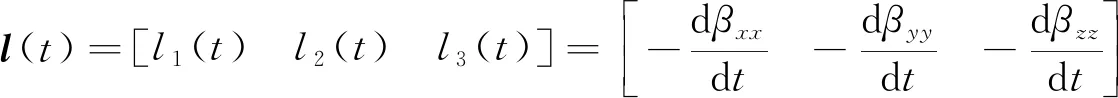
(3)

其中l1(t)、l2(t)为目标体横轴特征响应,l3(t)为目标体纵轴特征响应, 对轴对称物体, 两个横轴特征响应相同。为进一步简化正演模型, 对式(1)进行矩阵变形, 可得

V=γ(rd)p(t)

(4)

(5)

其中γ为位置矩阵, 与目标体的位置参数相关；p(t)为特征响应矩阵L的变形, 与目标体的特征响应和姿态角相关。通过矩阵变形将特征响应参数和位置参数分离, 使目标体电磁响应与特征响应参数呈线性相关, 以利于反演的简化。

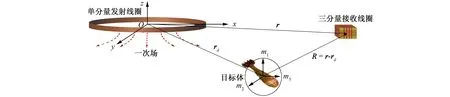
图3 瞬变电磁响应Fig.3 Transient electromagnetic response

2 反演算法优化

2.1 反演过程

反演过程就是用正演模型响应拟合实测响应确定待定参数, 将待定参数用向量v表示, 正演模型响应为Vmod(v), 实测响应为Vdata(v)。可通过最小二乘法寻找最佳待定参数v, 目标函数定义为Vmod(v)与Vdata(v)误差平方的最小值, 即

minimizeφ(v)=‖Vdata(v)-Vmod(v)‖2

(6)

基于磁偶极子正演模型采用分步反演法, 减少每一步需要反演的参数[13]。第1步采用DE算法反演目标体位置参数； 第2步由位置参数求得γ位置矩阵, 基于式(4)通过线性最小二乘法直接求解p(t), 进行矩阵变形得到特征响应矩阵L, 通过奇异值分解(SVD: Singular Value Decomposition)得到目标体特征响应l(t)。

为逐项优化影响反演计算效率的因素, 以82 mm未爆弹的瞬变电磁响应数据反演为例进行分析。

表1 目标体状态参数

未爆弹的状态参数如表1所示,x、y、z为未爆弹位于正交坐标系中的3个坐标,θ为未爆弹竖轴与z轴夹角,φ为未爆弹竖轴在xy平面投影与x轴夹角。探测测点设置如图4所示, 形成一组25个测点的响应数据Vdata。

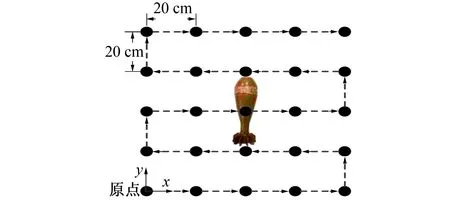
图4 测点设置Fig.4 Measuring point setting

2.2 目标位置反演

位置反演具体流程如图5所示, 首先将实测响应数据Vdata输入程序, 而后依次选取60道数据采用DE算法进行反演, 每道数据反演出一组位置参数, 最后将中间道反演出的位置参数取平均, 得到最优位置参数。采用DE算法逐道反演位置参数时, 建立初始位置参数种群, 种群中的每个位置参数均可求得γ矩阵, 磁极化张量p(t)可通过求解以下线性方程获得

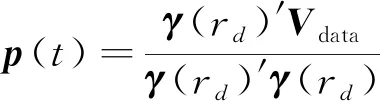
(7)

其中p(t)为这一道与γ最匹配的特征响应矩阵, 则目标函数可设置为

φ(v)=‖Vdata-γ(rd)p(t)‖2

(8)

应用式(8), 通过变异、 交叉、 选择形成下一种群位置矢量进行迭代, 达到最大代数或终止条件后停止迭代, 输出每道数据对应的最佳位置参数。

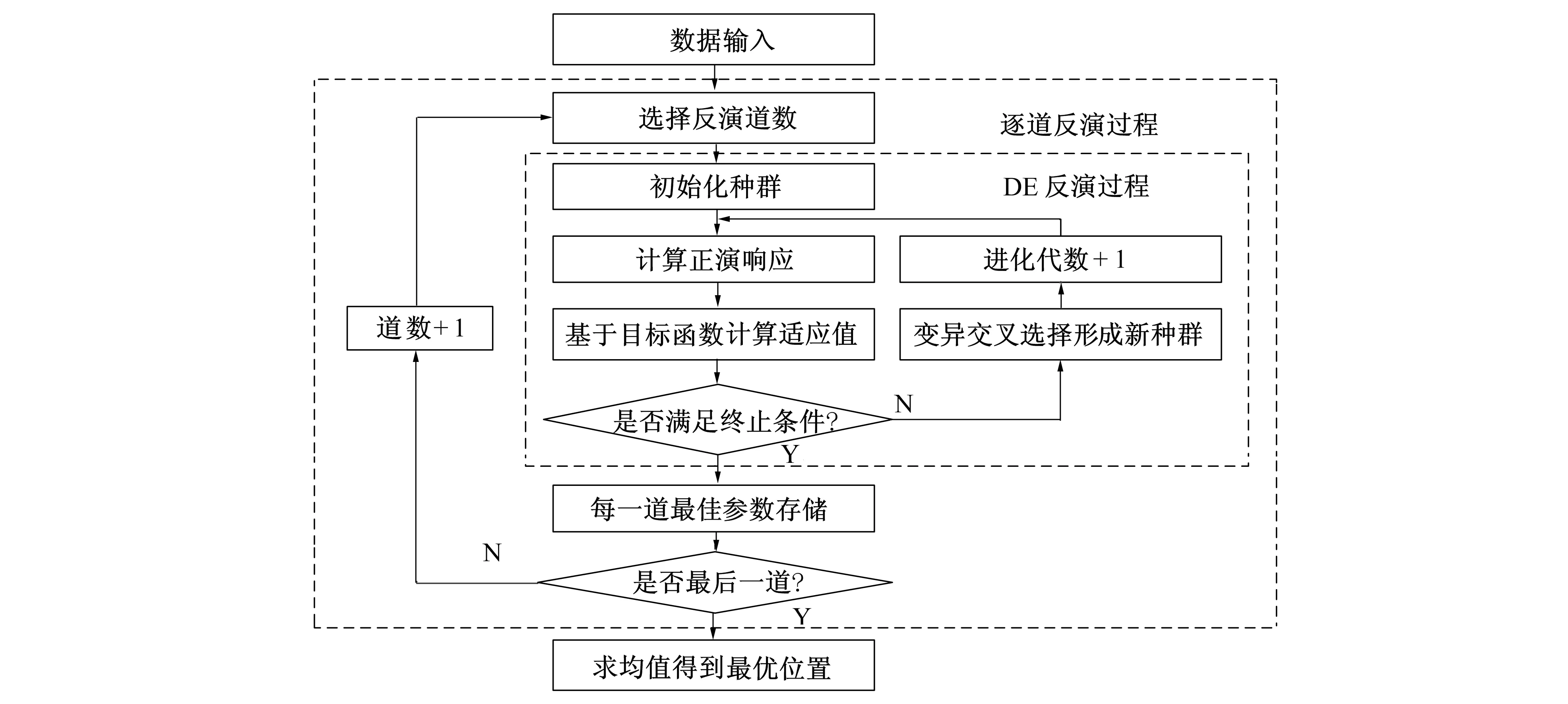
图5 反演流程图Fig.5 Flow chart of inversion

影响反演算法速度的因素主要有数据预处理中数据道数(CH: Channel)的选择和DE算法的种群数量(Np: Number of population)、 变异因子(F: Factor)、 交叉因子(CR: Crossover)、 最大进化代数(G: Generation)、 终止条件(CT: Condition of Termination)。常规DE算法各参数设置如表2所示。下面以82 cm未爆弹电磁响应数据Vdata反演为例对这些参数进行优化。

表2 参数设置

2.2.1 数据道数优化

探测系统获取的目标响应数据共60道, 每道数据通过反演均会得到一组位置参数, 最后得到60组位置参数, 图6为82 mm未爆弹的60道数据逐一反演所获取的位置参数。由于早期道信号幅度饱和, 晚期道信号信噪比低, 反演出的位置参数都不够准确, 一般选择中期20～40道数据反演出的位置参数取均值作为最优位置参数。常规DE反演方法需要逐一对这21道数据进行反演, 再对21组位置参数取均值得到一组最优位置参数, 这种计算方法需循环计算21次, 耗时较长。

从图6可以看出, 20～40道中每道数据反演出的位置参数较为一致, 说明在信噪比较高的情况下, 每道数据都能反演出准确的位置参数。为减少计算次数, 预先对20～40道响应数据进行取平均操作, 而后再进行反演计算, 既提高了信号信噪比, 保证了反演位置的准确性, 也大大减少了计算次数。

为验证反演结果的稳定性, 将常规DE反演与道数优化后DE反演分别计算10次, 并对反演结果和计算用时进行比较。位置反演结果如图7所示, 可见两种方法的反演的位置参数均一致, 误差在3 cm以内。反演用时如图8所示, 可见常规DE反演用时约140 s, 道数优化后DE反演用时约7 s, 计算用时大大减少。道数优化后DE算法在保证反演精度的同时较大提高了反演速度, 因此采用该方法进行反演计算。

图6 1～60道数据位置反演 图7 10次位置反演 图8 10次计算用时Fig.6 Position inversion of 1～60 data Fig.7 Position inversion of 10 cycles Fig.8 Time of 10 cycles

2.2.2 种群数量和最大进化代数优化

种群数量(Np)指待求位置参数向量v的规模, 主要影响种群的多样性和收敛速度,Np应大于位置参数的维度。最大进化代数(G)指最大迭代的次数, 主要影响收敛结果和计算用时。

为分析Np和G对反演结果的影响, 将Np依次设置为4～50之间以1为间隔递增的47个典型值, 将G依次设置为1～50之间以1为间隔递增的50个典型值进行反演, 并对反演结果进行分析。Np值对位置的影响如图9所示,G值对位置的影响如图10所示,Np/G用时如图11所示。

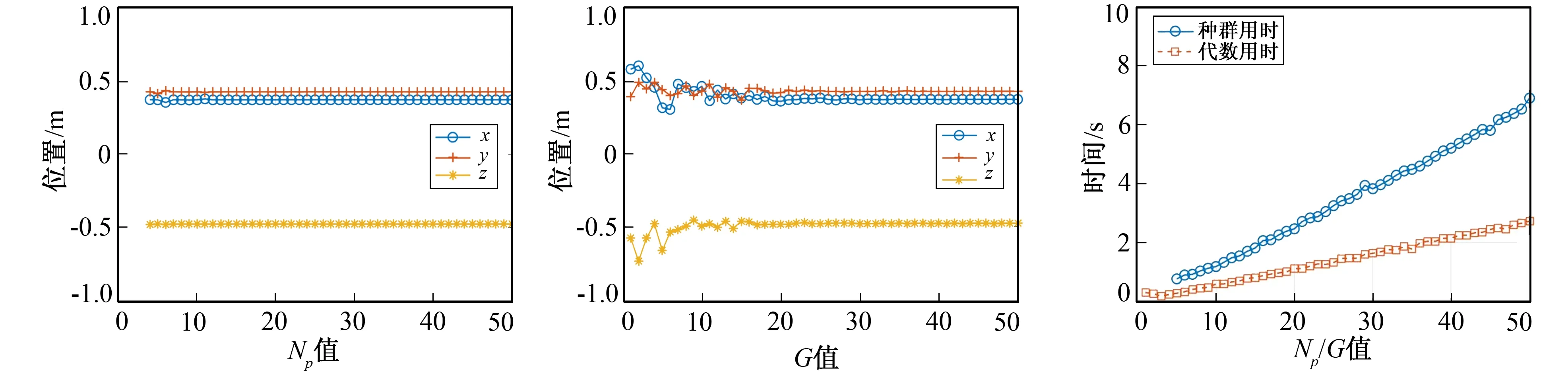
图9 Np值对位置的影响 图10 G值对位置的影响 图11 Np/G用时 Fig.9 Influence of Np on position Fig.10 Influence of G on position Fig.11 Time of Np/G

由图9、 图11可以看出,Np值在9以下时, 反演位置参数有一定波动；Np值在9以上时, 反演的位置参数均一致, 误差在3 cm以内, 计算用时随着Np值的增大而增加。为确保反演数据的准确性, 预留一定的冗余, 将Np设置为20。

由图10、 图11可以看出,G值在30以下时, 反演的位置参数有一定波动；G值在30以上时, 反演的位置参数均一致, 误差在3 cm以内, 计算用时随着G值的增大而增加。为确保反演数据的准确性, 预留一定的冗余, 暂时将G设置为40, 后续根据其他参数值的设置再进行优化。

2.2.3 变异因子和交叉因子优化

变异因子(F)是0～2之间的实常数, 主要影响算法的搜索步长。交叉因子(CR)是0～1之间的实常数, 主要影响算法进化信息的调整权重。为分析F和CR对反演结果的影响, 将F依次设置为0.1～2之间以0.1为间隔递增的20个典型值, 将CR设置为0.1～1之间以0.1为间隔递增的10个典型值进行反演, 并对反演结果进行分析。F值对位置的影响如图12所示,CR值对位置的影响如图13所示,F/CR用时如图14所示。

图12 F值对位置的影响 图13 CR值对位置的影响 图14 F/CR用时 Fig.12 Influence of F on position Fig.13 Influence of CR on position Fig.14 Time of Np /CR

由图12可以看出,F值在0.2～0.7之间变化时, 反演的位置参数均一致, 误差在3 cm以内。F为其他值时, 反演的位置参数有一定波动。由图14可以看出,F值变化时, 计算用时无明显变化。综上所述将F值设为0.5。

由图13可以看出,CR值在0.1～1之间变化时, 反演的位置参数均一致, 误差在3 cm以内。由图14可以看出,CR值变化时, 计算用时无明显变化。综上所述将CR值设为0.9。

2.2.4 终止条件优化

终止条件(CT)一般设置为某个最大进化代数或代价值小于某个阈值。目前每个参数设置如表3所示, 将DE算法每个参数按照表3中所示设置后, 循环运行程序10次观察反演过程中代价值的变化规律。

表3 参数设置

10次循环的代价值如图15所示。由图15可知, 每次循环代价值的大小都不同, 这是由每次循环初始种群数据的随机性造成的, 但最终在迭代25次后都开始趋于稳定, 说明DE反演经过25次迭代后, 就可以稳定收敛。为确保反演计算的准确性, 预留一定的冗余, 将终止条件设置为G=30, 并循环运行程序10次观察反演结果的稳定性和计算用时。位置反演情况如图16所示, 10次循环反演的位置全部一致, 误差在3 cm以内, 反演结果稳定性良好。计算用时如图17所示, 单次计算用时均值约2 s。综上所述, 将终止条件设置为G=30, 即最大进化代数为30代。

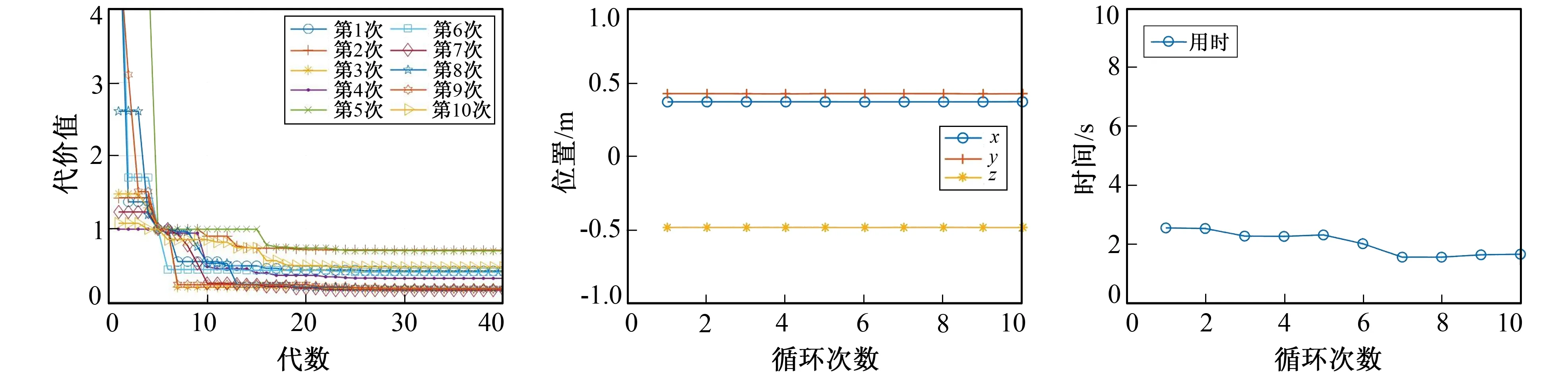
图15 10次循环的代价值 图16 10次位置反演 图17 10次计算用时 Fig.15 Cost value of 10 cycles Fig.16 Position inversion of 10 cycles Fig.17 Time of 10 cycles

2.3 目标特征响应反演

通过DE算法反演得到位置参数后, 根据得到的位置参数计算出γ(rbest)矩阵, 实测响应Vdata已知, 则p(t)可通过式(7)求解线性最小二乘方程获得。根据轴对称物体特征响应矩阵的对称性质, 将p(t)转换为L矩阵, 通过奇异值分解即可求得目标的x、y、z轴的特征响应

(9)

其中酉矩阵U为目标的姿态参数,lxx(t)、lyy(t)、lzz(t)为目标体的两个横轴和纵轴的特征响应。

3 实验结果

为便于对比分析, 数据处理使用内存为8 GByte、 CPU为AMD Ryzen5处理器的笔记本电脑, 数据分析软件为Matlab 2017版。实验选取5种未爆弹(U1～ U5)和4种未爆弹类似物(O1～ O4)作为测试目标, 目标体物理参数如表4和图18所示。应用便携式瞬变电磁系统获取9个目标体的瞬变电磁响应数据, 测点按照图4设置, 分别采用常规DE算法和优化DE算法反演目标的位置参数和特征响应, 并对结果进行比对分析。

表4 目标体物理参数

图18 目标体实物图Fig.18 Target photo

3.1 位置反演结果

表5为分别采用常规DE算法与优化DE算法对目标体位置进行反演得出的结果与计算用时。

表5 位置反演结果

如表5所示, 常规DE算法与优化DE算法反演出位置参数基本相同, 误差均在6 cm之内。优化DE算法的计算用时为常规DE算法的1.4%, 在保证反演位置准确性的基础上大大提高了反演效率。

3.2 特征响应反演结果

图19分别为采用常规DE算法与优化DE算法反演9个目标体的特征响应衰减曲线图, 从图19中可以看出, 两种反演方法获取的9个目标体的特征响应衰减曲线基本一致, 都能准确反演出目标体的特征响应。

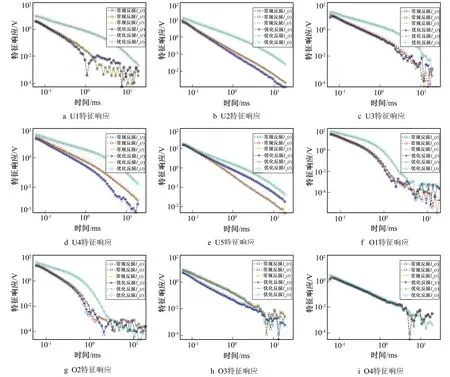
图19 目标体的特征响应曲线Fig.19 Characteristic response curves of 9 targets

其中U1～U5为轴对称未爆弹,x、y轴响应较小且衰减曲线基本相同,z轴响应较大； O1、O2为轴对称铁管,x、y轴响应较小且衰减曲线基本相同,z轴响应较大； O3为铁饼,x、y轴响应较大且衰减曲线基本相同,z轴响应较小； O4为铁球,x、y、z轴衰减曲线基本相同。

4 结 语

笔者利用吉林大学电磁传感技术实验室制作的便携式瞬变电磁系统获取未爆弹电磁响应数据, 基于磁偶极子正演模型采用DE算法反演目标的位置参数和特征响应。通过对数据预处理与DE算法参数的优化, 在保证反演精度的同时提高了瞬变电磁数据处理速度。在数据预处理优化过程中, 采用合并数据道数的方式, 减少了计算重复次数, 计算速度提高了20倍。在DE算法参数优化过程中, 以82 mm未爆弹的电磁响应数据反演为例, 逐项优化DE算法的最大代数、 种群数量、 变异因子、 交叉因子和终止条件, 在保证准确性的基础上, 再次将计算速度提高了3.5倍。

最后, 通过对9个目标体的电磁响应数据进行实际反演验证, 优化后的DE算法与常规DE反演算法都能准确获取目标体的位置参数和特征响应, 反演位置的误差在6 cm以内。优化后的DE算法在保证准确的基础上, 最终将计算用时减少至常规DE算法的1.4%, 达到了预期目标。如何优化探测测点的设置, 在较少的探测测点情况下实现对目标位置和特征响应快速准确反演, 将是下一步重点研究的内容。