泵站快速闸门上小拍门的水力损失特性分析

孙 翀,肖正友,张泽玉,陈松山*

(1.扬州大学电气与能源动力工程学院,江苏 扬州 225127;2.山东省调水工程运行维护中心,济南 250100)

立式或卧式轴流泵站常采用快速闸门断流,为防止快速闸门发生事故无法起门或开启速度过慢,引起轴流泵闭阀起动,造成电机严重过载,通常在快速闸门上装设小拍门．泵站快速闸门上小拍门的水力损失特性是影响水泵机组起动安全的重要因素．近年来,国内外学者采用数值模拟和模型试验方法对拍门水力特性进行了大量研究．杨帆等[1]利用数值模拟研究泵装置出口拍门的阻力损失,指出阻力损失与流量的平方不呈正比,泵装置效率下降值与拍门开度角亦非正相关;Zhou等[2]通过试验及数值模拟,得到在相同流量条件下,当上翻拍门开启角大于46°,下翻拍门开启角大于64°时,水力损失小于70 mm并趋于稳定;Xi等[3]对4种常用拍门开启角度不同流速下拍门后水流流态进行三维模拟和物理模型研究,发现出口涵洞沿线的阻力损失系数与开启角度呈负相关,拍门开启角度越大,出口涵洞中水流的水力损失越小,水流流态也逐渐变好;Wang等[4]研究不同安装形式、不同阀页、不同材料的拍门开启角度和冲击力,得到翻式拍门冲击力为单拍门冲击力的42%,盖板式双拍门为单拍门的49%;徐辉等[5]基于铺层网格及动网格技术对带小拍门的轴伸贯流泵快速闸门三维过渡过程进行数值模拟,指出机组启动过程中泵段扬程先增大后减小至额定扬程,2.25 s时出现最大启动扬程6.38 m;Yu等[6]对拍门关闭过程中3个典型时刻下的出水池流场进行数值模拟,认为分流墩可改善流速均匀度．但上述研究多为泵站出口单独设置拍门,针对快速闸门上小拍门的研究较少,并且未考虑多因素组合对水力损失特性的影响．本文以浙江省某泵站为研究对象,拟设计不同孔口面积和不同开度角的拍门,通过水泵装置模型试验,研究不同工况、不同开度、不同孔口尺寸下拍门的水力损失特性,以期为实际工程应用提供依据．

1 模型水泵装置与试验方案

1.1 模型设计

以浙江省某泵站为研究对象,该泵站单机设计流量20 m3·s-1,扬程2.42 m,水泵叶轮直径2 200 mm,转速187.5 r·min-1．泵站采用肘型进水流道和虹吸式出水流道,出水流道出口设置两道快速闸门,分别为工作闸门和事故闸门,工作闸门上设置双扇对称小拍门,具体位置如图1(a)所示．为研究工作闸门上小拍门的水力损失特性,设计制作模型水泵装置．模型泵叶轮采用TJ04-ZL-06水力模型,叶片数为3片,导叶数为6片,叶轮直径为300 mm,进出水流道按叶轮直径比3∶22缩小,利用钢板焊接制作,内部喷涂聚氨酯漆,满足糙率相似要求．水泵装置模型如图1(b)所示．

图1 泵站设计方案及模型泵装置Fig.1 Design scheme and Model experimental device

1.2 拍门设计

拍门采用钢板制作,安装在模型泵装置出水流道工作闸门上,如图2所示．根据原型与模型相似几何比尺7.333,计算得出模型工作闸门宽为826.18 mm,高为358.55 mm．设计4种对称拍门孔口,拍门宽分别为314,279,236,183 mm,拍门高分别为205,182,154,119 mm,拍门孔口面积A与工作闸门面积A0的比值A/A0分别为44%,35%,25%,15%．拍门开度角为拍门与垂直面之间的夹角α,如图3所示．试验中通过在拍门后设置两个定位支撑杆来固定拍门开度角，设计拍门开度角分别为20°,35°,50°,65°,80°．

图2 拍门照片Fig.2 Photo of the real flap door

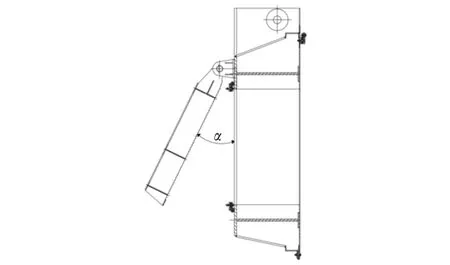
图3 拍门开度角示意图Fig.3 Schematic diagram of flap door opening

1.3 试验参数

水泵装置模型试验在扬州大学高精度泵站试验台进行．试验台为封闭循环系统,由水力循环系统、动力系统、控制系统和测量系统组成,其中水力循环系统包括进水箱、出水箱、储水箱、辅助泵、管道及控制阀门等．模型泵装置安装在进水箱和出水箱之间,如图4所示．

图4 试验系统示意图Fig.4 Schematic diagram of test bench

拍门水力损失特性Δh(Q)可表示为工作闸门全开时的水泵装置流量-扬程曲线H1(Q)与工作闸门关闭小拍门打开时的水泵装置流量-扬程曲线H2(Q)的差值,即Δh(Q)=H1(Q)-H2(Q),因此,模型试验应测流量Q和水泵装置扬程H．其中流量测量采用精度等级为0.2级的OPTIFLUX2300W DN400电磁流量计(科隆公司,德国),水泵装置扬程测量采用精度等级为0.1级的EJA压差传感器(横河电机株式会社,日本)．

2 结果与分析

2.1 模型泵水力特性

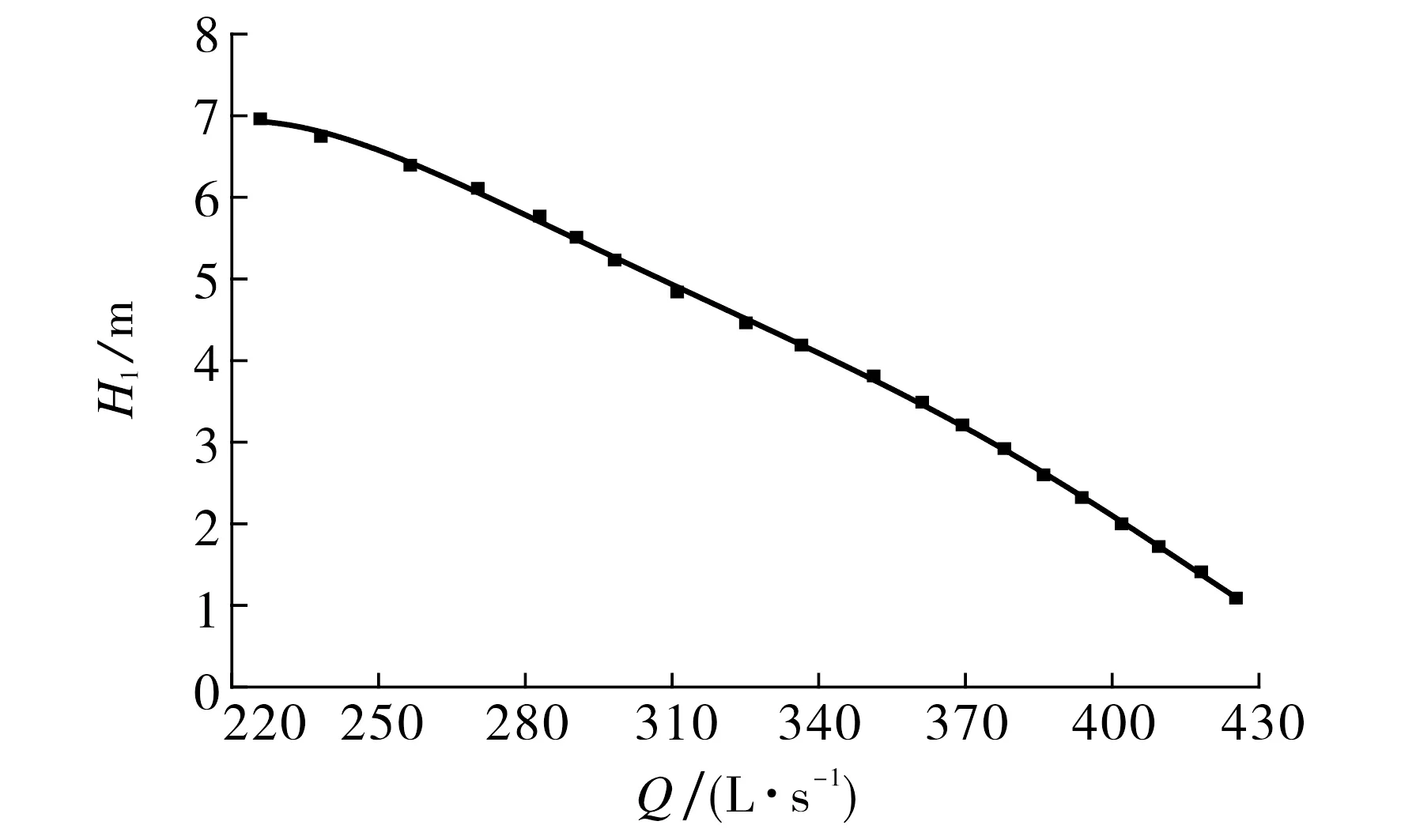
图5 工作门全开时的流量-扬程曲线Fig.5 Q-H1diagram when flap valve fully opened

根据欧拉准则确定水泵转速为1 375 r·min-1,试验中转速保持不变,测试工作闸门全开时模型泵装置的能量特性,结果如图5所示．由图5可知,模型水泵装置扬程随流量的增大而减小,最大扬程为6.96 m,此时流量为225.82 L·s-1,最小扬程为1.09 m,此时流量为425.30 L·s-1,当扬程下降5.87 m时,流量增大了199.48 L·s-1．

测试工作闸门关闭条件下小拍门打开不同孔口面积和不同开度角时模型泵装置的能量特性,结果如图6所示．由图6可知,拍门孔口面积比相同时,随拍门开度减小,水泵装置流量-扬程曲线整体向左偏移,但并非随拍门角度变化呈线性偏移,当拍门开度角为50°～80°时,偏移量小,而拍门角度小于50°时,偏移量明显增大;水泵装置流量-扬程曲线斜率随孔口面积比减小而增大,曲线整体向左偏移,拍门开度和流量均相同时,孔口面积比越小,水力损失越大．

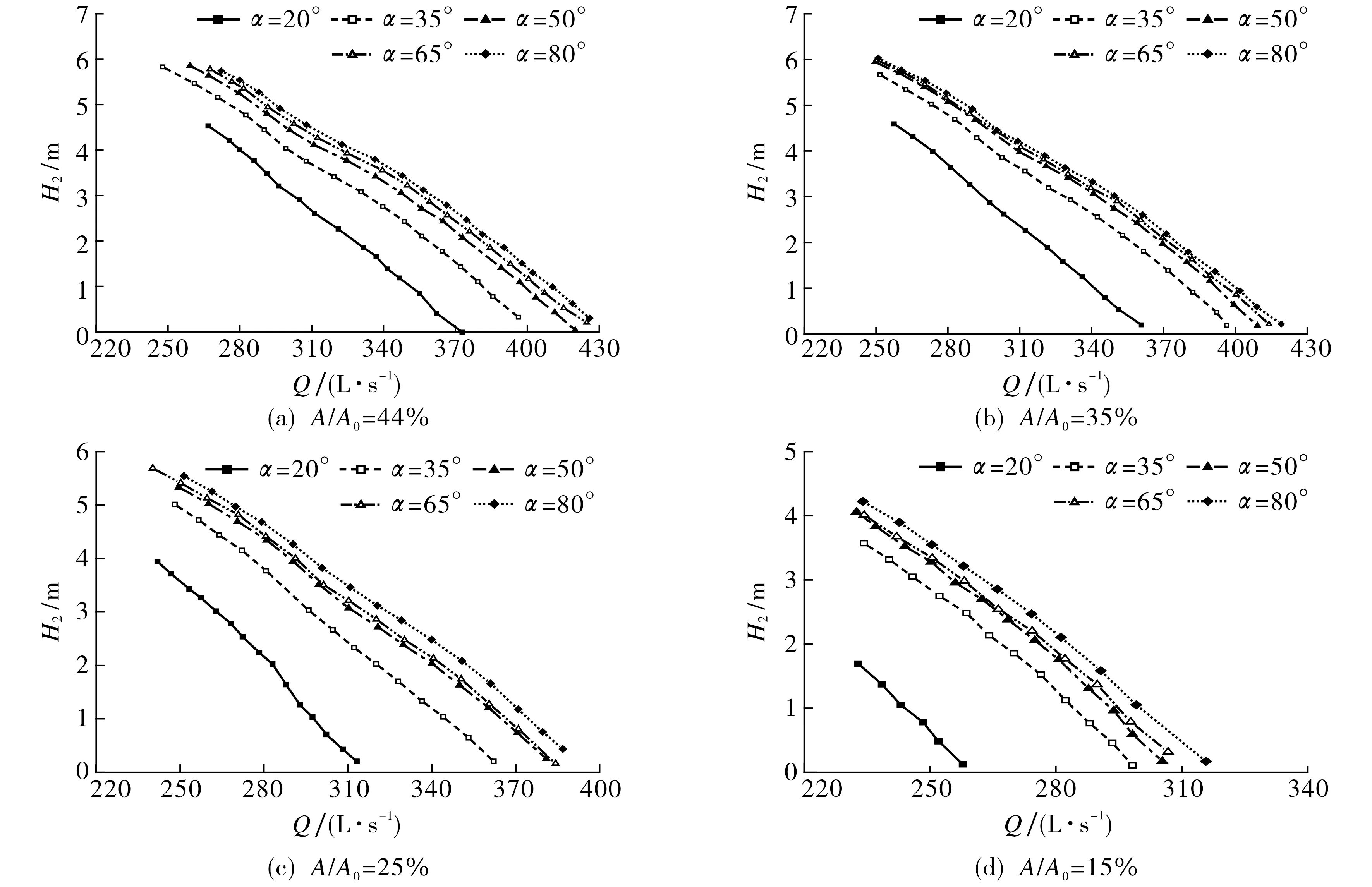
图6 不同孔口面积比不同拍门开度角下的流量-扬程曲线Fig.6 Flow-head curve under different opening areas and opening degrees

根据拍门水力损失特性Δh(Q)=H1(Q)-H2(Q),将图5和图6中能量特性曲线拟合得到的5次多项式相减,得到水力损失的5次多项式系数,以此获取流量范围,在此区间等间距取若干个点,代入水力损失5次多项式函数,得到不同工况下的水力损失特性,结果如图7所示．由图7可知,开度角越小,孔口面积越小,水力损失越大,最大水力损失可达6.12 m,最小水力损失仅为0.34 m,最大值为最小值的18倍．

图7 不同孔口面积比不同拍门开度角下水力损失特性Fig.7 Hydraulic loss diagram of flap door with different opening areas and opening degrees

2.2 拍门水力特性

为了研究不同因素对局部水力损失系数的影响,将图7试验结果参数无量纲化,得到不同孔口面积比和不同拍门开度角下的水力损失特性,如图8所示．由图8可知,孔口面积比相同时,拍门开度角越小,局部水力损失系数越大;拍门开度角相同时,孔口面积比越小,局部水力损失系数越大;局部水力损失系数随Froude数变化的变动范围较小,即Froude数对局部水力损失系数的影响较小．

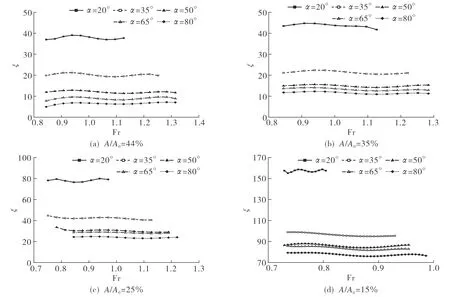
图8 无量纲拍门水力损失特性Fig.8 Dimensionless diagram of hydraulic loss

根据前述分析,局部水力损失系数函数可简化为ξ=f(A/A0,α)．图9为局部水力损失系数与不同拍门开度角和不同孔口面积关系．由图9(a)可知,局部水力损失系数随开度角的增大而减小;当开度角小于35°时,随开度角减小,局部水力损失系数急剧增大;当开度角大于50°时,局部水力损失系数渐趋平缓．由图9(b)可知,局部水力损失系数随拍门孔口面积比的增大而减小;当孔口面积比小于25%时,随孔口面积比减小,局部水力损失系数急剧增大;当孔口面积比大于35%时,局部水力损失系数变化平缓．综上分析,在工程实际中应尽量避免拍门开度角小于35°、孔口面积比小于25%．

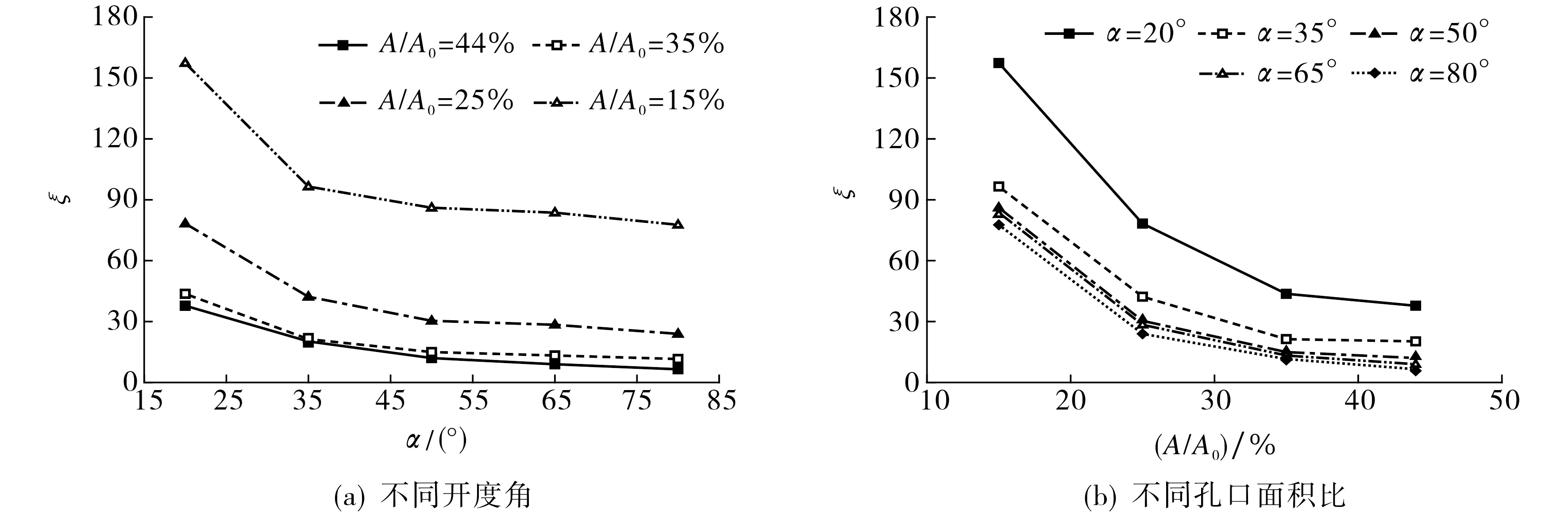
图9 局部水力损失系数变化规律Fig.9 Variation law of local hydraulic loss coefficient

2.3 局部水力损失系数

借助现代神经网络[7-10]学习方法计算局部水力损失系数,构建具有1个隐含层的反向传播(back propagation,BP)神经网络,模型设定输入层2个神经元,隐含层6个神经元,输出层1个神经元．

BP神经网络的输入列向量X=(α,A/A0)T,隐含层神经元输入Z1=W1X+b1,其中W1和b1分别为从输入层到隐含层的权重系数矩阵和阈值．隐含层采用双曲正切S型转移函数,即tansig函数f1(x)=(1-e-2x)/(1+e-2x)．输出层神经元输入Z2=W2f1(Z1)+b2,其中W2和b2分别为从隐含层到输出层的权重系数矩阵和阈值．输出层采用purelin线性传递函数,得到局部阻力系数预测值ξ′,输出误差函数E(W,b)=(ξ-ξ′)2/2．按照W-H学习规则,基于误差函数的最小均方差,修正权重系数矩阵和阈值．

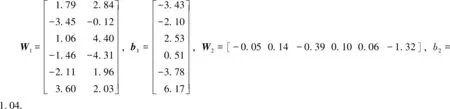
3 结论

1) 拍门水力损失系数与孔口面积和拍门开度的曲线呈非线性单调变化,变化曲率随孔口面积和拍门开度减小而增大,流道出口Froude数对拍门水力损失系数的影响较小．

2) 拍门水力损失系数在拍门开度角小于35°,孔口面积小于25%处的曲率明显增大,工程设计中应尽量避免出现此类工况．

3) 通过BP神经网络训练,得到小拍门局部阻力系数的权重系数矩阵和阈值,可预测任意开度角和孔口面积比下的拍门局部水力损失系数．