任意两个平面多边形螺线线圈间互感系数的解析模型

吴德会，陈红富，王晓红

(厦门大学航空航天学院，福建厦门361102)

平面螺线线圈已广泛应用于传感器领域，如涡流传感器[1]、无源无线传感器[2-3]、植入式生物医学传感器[4]、核磁共振传感器[5]、位移传感器[6]和阵列涡流传感器[7]等.其中，平面螺线线圈之间的互感(mutual inductance，MI)系数是上述传感器和执行器设计和优化的重要基本参数.

因此求解具有明确物理意义的MI系数公式始终是一个有意义的问题，它可以为设计人员提供直观的见解.在现有的文献中，有几种计算各种几何形状线圈之间的MI系数的方法，包括麦克斯韦公式[8]、Greenhouse方法[9]、格罗弗方法[10]和诺依曼积分[11].在这些方法中，Greenhouse方法是一种较为有效的方法：一个多匝线形线圈中总的MI系数是其两两单匝平行线圈之间的MI系数之和(M总=M1，2+M1,3+…+M1,n).然而，Greenhouse方法通常只适用于线形线圈，并且该方法一般需要计算机的辅助和繁琐的初始值设置，操作性极其不便.

在现如今的研究中，也有大量关于圆形和矩形线圈的MI系数计算，但是关于八角形和六边形线圈的MI系数研究却很少.又因为八角形和六边形线圈在品质因数方面比矩形线圈具有更好的性能[12].因此，六边形和八边形线圈的MI系数计算是一项有意义的研究.

据本文作者所知，六边形和八边形线圈的MI系数仅Tavakkoli等[13]研究过，Tavakkoli等将次级线形线圈的面积细分为多个三角形区域和正方形区域，并分别通过积分计算这些区域的相应磁通量，然后得出总的MI系数为次级线圈上的总磁通量之和与激励电流的比值.但该方法需要分别计算多个不同区域的磁通量，计算表达式比较复杂，并且该公式中两线圈仅仅是同轴分布，没有考虑线圈使用的实际情况，如线圈是存在相应横截面以及没有考虑初级(TX)线圈和次级(RX)线圈在实际传感器应用中错位分布的情况，并且Tavakkoli等[13]的方法仅适用于六边形和八边形线圈，不适用于其他多边形线圈.

本文针对现有问题，将任意多边形螺线线圈划分为多个三角形区域，统一的区域划分简化了计算步骤，基于二阶矢量位(SOVP)并引入顶角坐标，优化了复杂的MI系数计算公式，并且在公式中考虑了线圈横截面这一几何参数以及线圈之间的空间位置布局，从而更符合传感器实际应用情况.

1 多边形线圈的电磁场

1.1 多边形线形线圈

根据参考文献[13]可知，螺线线圈可以被近似为一组同心单匝线圈.所以首先考虑具有n条边的单匝多边形线形线圈的情况，如图1所示.任意形状线形线圈的电磁场问题可以使用SOVP公式解决.根据Theodolidis等[14]的标量势计算公式可得该线形线圈初级场标势Wε：

{∬Se-i(axs+bys)dxsdys}dadb,

(1)

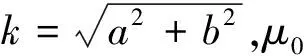
图1 n边形线形线圈Fig.1Polygonal filament coil with n-sides

与Tavakkoli等[13]的方法不同，本文将区域S细分为n个三角形子区域.由顶点(xi,yi)、(xi+1,yi+1)和原点O组成的子区域表示为Si,其中：i表示多边形的第i个顶点，即以顶点(x0,y0)为第零个点，按逆时针数多边形的第i个顶点.如图2所示，子区域Si表示为：

(2)

其中，ki,ki+1,ki,i+1是三角分区中三条边的斜率.设

(3)

(4)

对于具有n条边的多边形区域S,有

(5)

(6)

1.2 带横截面的多边形线圈

假设TX线圈中的导体横截面为矩形δ×w,其中，δ为线圈厚度，w为线圈宽度，而RX线圈中的导体横截面为δ′×w′,如图2所示.

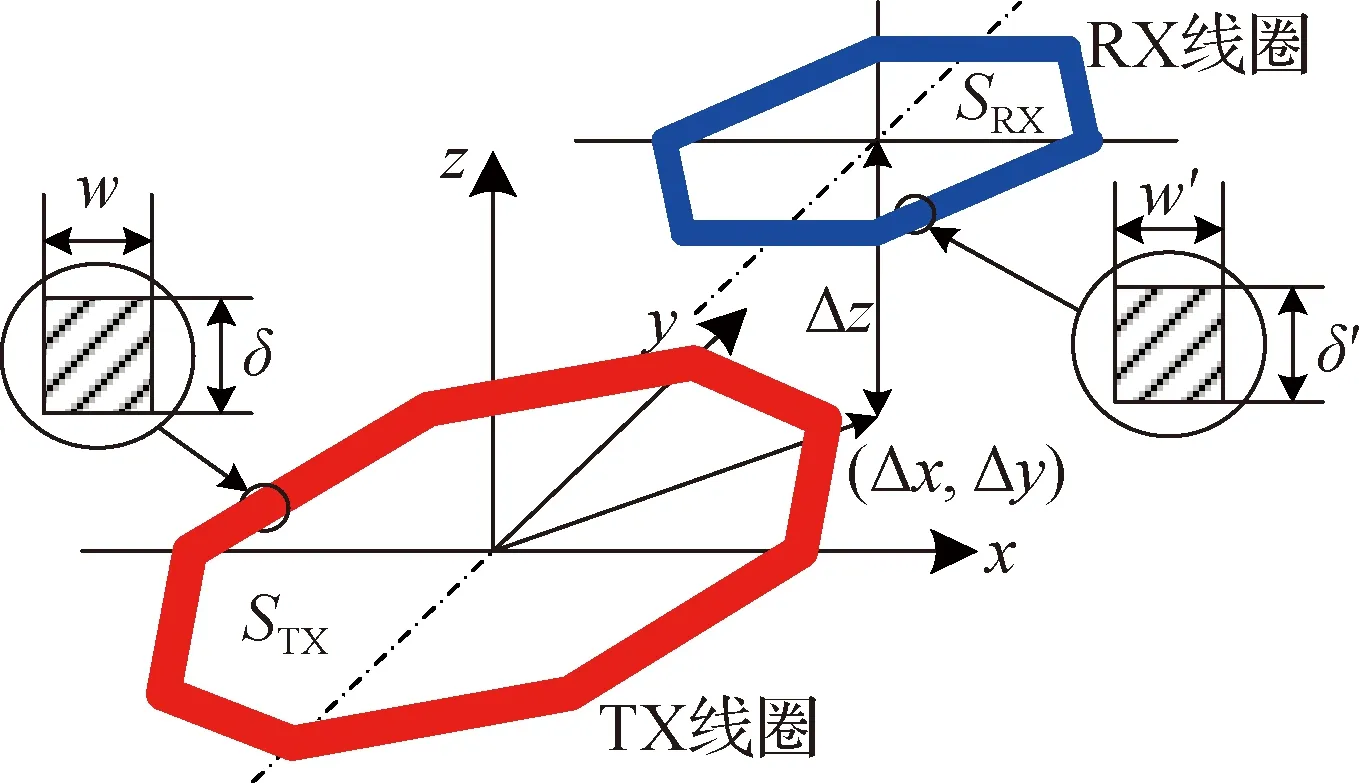
图2 两个带横截面的错位分布的单匝多边形线圈Fig.2Two misaligned single-turn polygonal coils with cross-sections

可以推导出单匝TX线圈的标量势Wsingle：

(7)

平面多匝螺线线圈如图3所示，根据叠加原理，一个N匝螺线线圈的总标量势可以被表示为：

(8)

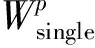
为了计算方便，引入极坐标，即a=kcost,b=ksint.定义螺线线圈函数为Cspir,并将式(6)代入，可得

(9)

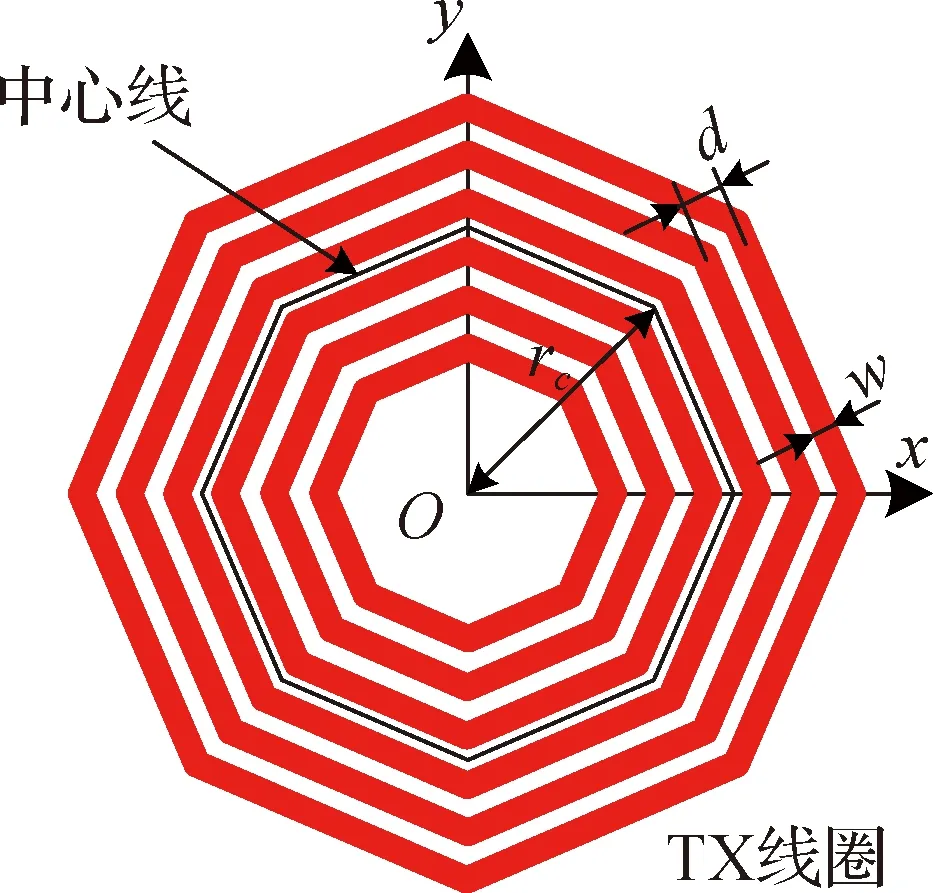
图3 具有n条边的 N 匝多边形螺线线圈(俯视图)Fig.3N-turns polygonal spiral coils with n-sides (top view)

从图3中不难看出，第p匝的顶点坐标(xp,i,yp,i)可以用极坐标表示为：

(10)

其中，rc是中心线半径，d是线间距.

将式(10)代入式(9)，可以得简化表达式：

(11)

2 多边形螺线线圈的互感模型

(12)

其中，S表示线形线圈所围成的区域，s表示线圈横截面区域.

将式(8)和(11)代入(12)得到，

Φ=

(13)

定义螺线线圈函数的复共轭为：

(14)

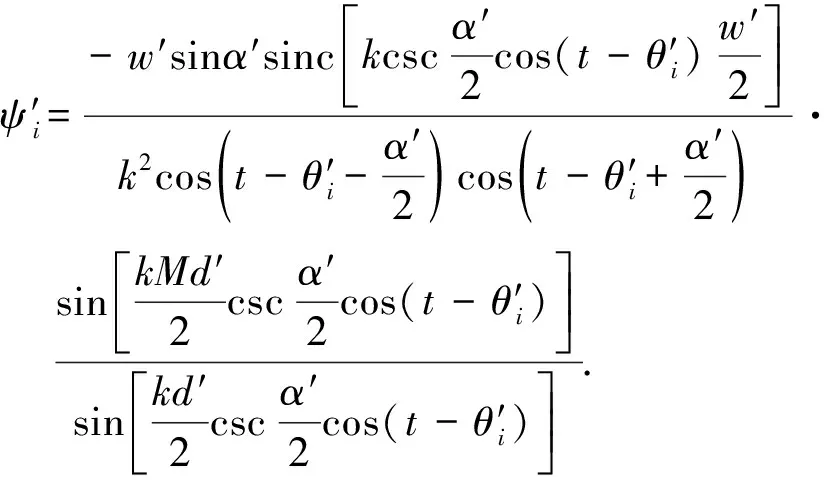
此外，假设与 RX 线圈存在横向错位(Δx,Δy),可以进一步将螺线线圈函数的复共轭重新定义为：

(15)

式(13)中变量的积分z表达式可以由下式推导出

(16)

其中Δz是TX和RX线圈之间在Z方向上的距离.

将式(15)和(16)代入(13)，可以得到MI的计算公式：

(17)

由此可见，式 (17)是任意两个多边形螺线线圈之间MI通用计算公式. TX线圈是具有n条边且横截面为δ×w的N匝螺线线圈，RX线圈是m边且横截面δ′×w′的M匝螺线线圈.与现有研究相比，本文所提出的计算模型可以避免每匝线圈之间所有可能组合的互感叠加计算，大大简化了计算流程.

3 实验验证

为了验证所提出的模型的可行性，使用PCB技术分别制作了八边形螺线线圈和六边形螺线线圈(图4).实验中使用的八边形和六边形螺线线圈的尺寸分别列于表1中.

图4 螺线线圈示意图Fig.4Schematic diagram of spiral coil

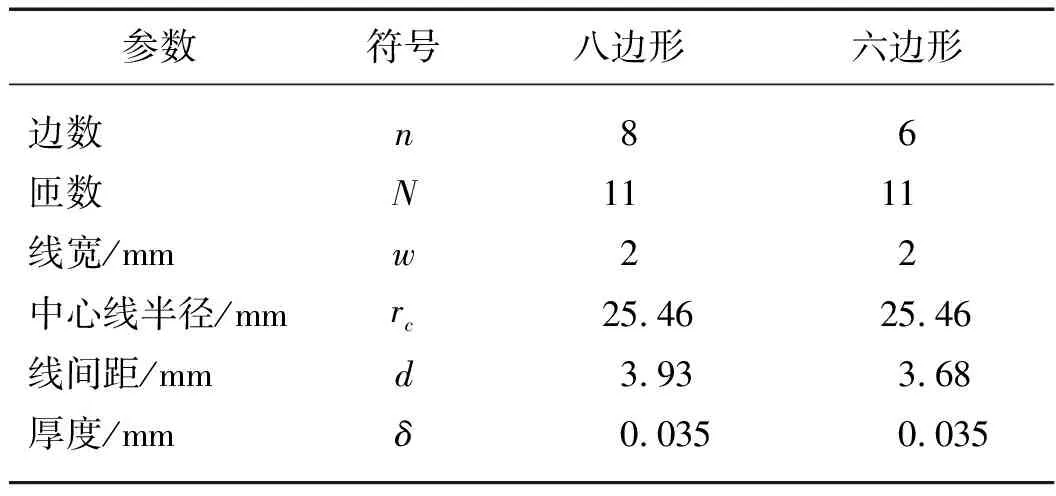
表1 螺线线圈的几何参数

为了开展实验研究，搭建了如图5所示的实验平台，以测量两个错位线圈之间的互感.该实验平台主要由HIOKI IM3523 LCR 测量仪、PCB线圈、换向开关等组成.

为了证明本文提出的互感计算模型很好地适用于两种不同形状的螺线线圈，因此在接下来的实验中以八角形螺线线圈作为TX线圈和六边形螺线线圈作为RX线圈. TX线圈和RX线圈之间的纵向间距Δz、横向错位(Δx,Δy)皆可调.

图5 测量互感的实验装置Fig.5Experimental setup for measuring MI between two misaligned coils

(18)

如图6所示，通过改变Z方向的间距和X与Y两个方向的错位距离，设置两组验证实验.在实际实验过程中，使用LCR测量仪在最大激励频率200 kHz下测量同相和异相两个线圈之间的电感.

图6 两个多边形线圈的位置分布Fig.6Layouts of two polygonal spiral coils

第一组实验，两个螺线线圈最初是同轴排列的(即Δx=Δy=0)然后X-方向横向错位Δx=20 mm与Y-方向横向错位Δy=20 mm,如图6(a)所示.在三种位置情况下，改变两线圈Z-方向之间的间距，从10 mm逐渐增加到100 mm，每次变化的间隔为10 mm.为了验证模型的准确性，使用Mathematica 12.0数学软件对式(17)进行求解，得到相应MI的理论值.计算与实测结果如图7所示.

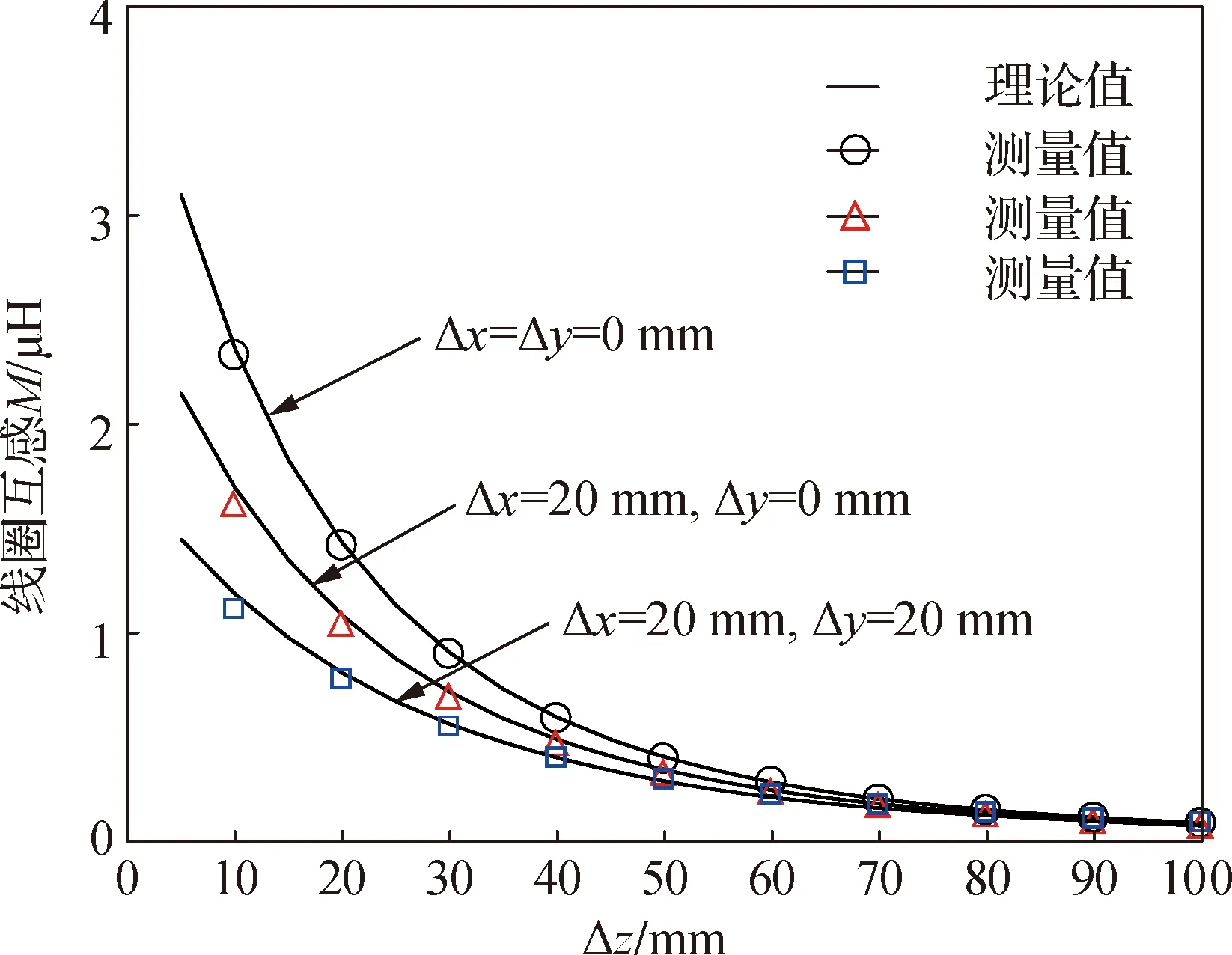
图7 Z方向间距变化的线圈之间的互感Fig.7MI between two polygonal spiral coils with distance change

由图7可知，互感的测量值与理论值吻合度很高，其中最大误差数值为0.040 9 μH,最小误差数值为0.004 7 μH,平均误差数值为0.026 04 μH,相对误差均小于2.5%.这些实验结果表明所提出的模型可以有效地解决两个不同形状的多边形螺线线圈之间的MI系数随间距变化的计算问题.

第二组实验进行横向错位实验.将两线圈Z方向的间距固定为10 mm，Y方向错位分别设置为0 mm、20 mm和30 mm，如图6(b)所示.同时，X方向错位从0 mm逐渐变为100 mm，间隔为10 mm.使用所提出的方法计算错位分布的两个线圈之间的互感，并与测量值进行比较.结果如图8所示.

图8 横向错位变化的线圈之间的互感Fig.8MI between two polygonal spiral coils with lateral misalignment

从图8中可以看出，所提出的方法也可用于有效地计算未对准的MI.理论值和测量值之间的相对误差约为3%.这种微小的差异可能是由于测量设置中的缺陷造成的，例如纵向间距、横向错位、线圈的几何参数以及连接器引起的寄生电感.

将本文算法与Tavakkoli方法的计算速度进行对比，结果如表2所示，虽然计算速度相当，但是本文提出的公式更具有通用性.

表2 本文提出的方法与Tavakkoli方法计算速度对比

4 结 论

1) 本文推导了正方形、五边形、六边形、八边形等任意两个正多边形螺线线圈之间互感计算的一般解析公式. 两个线圈可以是不同的线圈尺寸和几何形状，例如，八边形线圈作为TX线圈和六边形线圈作为RX线圈.

2) 使用所提出的公式解决的布局不仅包括同轴，而且包括不同方向的横向错位.在分析模型中同样考虑了导体的横截面，这更符合实际线圈的情况.

3) 在本文提出的互感计算公式中，两平面螺线线圈之间的互感直接使用TX线圈和RX线圈的系数计算.从而有效地避免了计算每匝线圈之间所有可能组合的互感叠加，因此本文提出的新互感计算公式比之前的更简便.