风扰和故障条件下集群无人机强化学习自适应容错协同控制

余自权，程月华，张友民，姜 斌*

(1.南京航空航天大学自动化学院，江苏南京210016；2.加拿大康考迪亚大学机械、工业与航空工程系，蒙特利尔H3G 1M8)

集群无人机逐渐被用于执行广域监视、资源勘查、森林火情检测等复杂、危险且耗时的任务[1-3].与单架无人机只能挂载少量特定类型的任务载荷相比，集群无人机可以挂载庞大数量和多种类型的任务载荷.通过将不同任务载荷分配至不同的无人机，集群无人机可以协作完成单架无人机难以完成的任务[4].目前，国内外均已开展集群无人机的相关研究，例如：国内中国电子科技集团电子科学研究院完成的119架(2017)和200架(2018)无人机集群飞行试验；国外的“小精灵”项目、“低成本无人机集群技术”项目等.集群无人机协同执行任务涉及感知技术、通信技术、计算机技术、控制技术和管理技术，为典型的“感-传-算-控”系统，属多学科交叉研究领域[5].在上述技术中，控制技术主要用于确保集群无人机系统协同编队的稳定性[6].比较典型的协同编队控制架构包括基于领航-跟随、行为、虚拟结构和图论的控制架构[7].基于上述控制架构，神经网络自适应、滑模、有限时间、势能场等控制方法被广泛用于集群无人机的协同控制中[8-9].

集群无人机协同执行任务过程中经常会遭遇阵风、风切变、常值风等外界风扰的影响，给整个集群编队的安全控制带来极大的挑战.此外，集群无人机编队飞行过程中可能会遭遇致命性和非致命性故障[10].在突遭致命性故障情况下，如何将完全失效无人机从集群编队中移除而不碰撞邻近无人机，并且确保通信拓扑变换后的编队稳定性是亟待解决的关键性难题之一.另外一个关键性技术难题是当集群无人机遭遇非致命性故障时，如何利用硬件冗余或者容错控制算法确保故障集群编队依旧能较好地完成既定任务.在非致命性故障情况下，集群无人机容错飞行控制算法的设计主要面临如下挑战性问题：1) 外界风扰与集群内部故障耦合情况下的容错协同控制问题；2) 考虑性能强约束需求的集群容错协同控制问题；3) 机间通信中断/网络攻击下的集群容错协同控制问题；4) 集群无人机分布式故障诊断与容错协同控制的集成设计问题；5) 面向故障执行器二次损伤防护的平稳快响容错协同控制问题；6) 考虑输入、状态、输出约束下的容错协同控制设计[10].为提升集群无人机编队遭遇非致命性故障情况下的飞行安全性，基于预设性能函数，Yang等[11]针对多架三自由度无人直升机设计了分布式协同控制策略，确保了无人机编队在遭遇故障、不确定性和输入饱和情况下的飞行安全性.Yu等[12]采用分布式滑模估计器与容错控制分层设计架构，基于神经网络学习算法、最小参数学习方法和一阶滑模微分器设计了集群固定翼无人机有限时间容错协同控制方案，提升了集群无人机遭遇故障情况下的编队飞行安全性.Yu等[10]针对集群无人机容错协同控制研究的历史及现状，以及未来可能的研究方向进行了详细分析，并阐述了目前用于容错协同控制研究的方法.

作为一种可用于解决强非线性控制问题的强化学习方法，Actor-Critic强化学习方法集成了基于Value的Q-Learning方法和基于Policy的Policy Gradients方法，其中Critic神经网络用于评估控制行为，Actor神经网络基于Critic神经网络评估结果修正控制信号.与四旋翼无人机的运动特性相比，固定翼无人机具有较强的非线性，并且各个控制通道之间存在强耦合特性[13-14].将强化学习机制引入集群固定翼无人机容错协同控制设计中，可以有效解决风扰、故障、强非线性耦合影响下的容错协同控制设计难题.最近，越来越多的研究者开始在非线性控制设计中引入强化学习机制，以提升控制方案的学习能力[15-19].Xian等[15]针对遭遇外界干扰与系统不确定性的小型无人机，设计了Actor神经网络和Critic神经网络，分别用于估计未建模动态不确定性和跟踪性能函数，并构建了基于Actor-Critic神经网络的强化学习鲁棒自适应控制策略，确保了无人机的飞行安全.Shi等[16]针对无向通信拓扑下的多航天器姿态编队控制问题，引入预设性能函数，设计了可在线补偿系统不确定性和估计代价函数的Actor-Critic神经网络强化学习机制，提出了一种航天器智能编队控制方法，满足航天器编队跟踪性能预设要求.Elhaki等[17]进一步采用基于Actor-Critic神经网络的强化学习策略，研究存在未建模动态和不确定性的欠驱动自主无人潜航器跟踪控制问题，提出了基于强化学习机制的鲁棒自适应神经网络控制方法.虽然目前基于强化学习机制的控制研究已取得部分成果，但针对遭遇风扰、故障下的集群固定翼无人机强化学习容错协同控制研究还较少，亟待进一步研究.

基于上述分析，本文将针对外界风扰与内部故障耦合影响下的集群无人机容错协同控制问题，结合强化学习机制，研究集群无人机容错协同控制方法，确保集群无人机在遭遇非致命性故障和风扰情况下可同步跟踪上参考指令信号.

1 理论基础

1.1 无人机数学模型

本文研究N架固定翼无人机集群编队飞行过程中遭遇风扰与执行器故障情况下的容错协同控制方案，其中，第i架无人机的姿态动力学模型可表示为[20]：

(1)

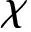
(2)

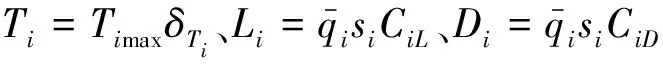
进一步地，第i架无人机的姿态角速率运动模型可表示为：

(3)

(4)

其中：Cil0、Cilβ、Cilδa、Cilδr、Cilp、Cilr、Cim0、Cimα、Cimδe、Cimq、Cin0、Cinβ、Cinδa、Cinδr、Cinp和Cinr为气动力矩系数.

基于式(1)～(3)，可得：

(5)

其中：fi11、fi12、fi13、di11、di12和di13具有如下的表达式：

(6)

其中：fi

χ

0、fiγ0、di

χ

和diγ可表示为：

(7)

(8)

将气动参数表达式(4)带入角速率式(3)，可得：

(9)

(10)

定义xi1=[μi,αi,βi]T、xi2=[pi,qi,ri]T、ui=[δia,δie,δir]T，则可以获得如下姿态模型：

(11)

其中：fi1=[fi11,fi12,fi13]T，fi2=[fi21,fi22,fi23]T，di1=[di11,di12,di13]T，gi1和gi2的表达式如下：

(12)

(13)

考虑副翼、升降舵、方向舵执行器效率下降和作动偏差故障，则可获得如下面向控制的故障无人机模型：

(14)

其中:ρi=diag{ρi1,ρi2,ρi3}为效率下降矩阵，bif=[bif1,bif2,bif3]T为有界作动偏差向量，ρiv=1代表第v个执行器未遭遇故障；ρiv∈(0,1)代表第v个执行器遭遇了效率下降故障，v=1, 2, 3分别代表副翼、升降舵、方向舵.

1.2 分数阶微积分

将分数阶微积分引入整数阶系统中可以有效改善控制系统的暂态和稳态性能[21]，本文采用下述分数阶微积分进行控制器设计[22]：

(15)

其中：a∈(n-1,n]为分数阶微积分算子，n∈N.Γ(·)是Gamma函数.

针对微积分定义(15)，存在如下等式[23]：

(16)

1.3 神经网络

本文采用神经网络设计强化学习算法.神经网络的结构包括输入层、隐含层和输出层，当隐含层的神经元节点数量足够大时，可以用来逼近强未知非线性函数.神经网络学习结构可以表示为[24]：

f(z)=wTφ(z)+ε,

(17)

其中：z为神经网络的输入向量，w和φ分别代表神经网络的最优权重矩阵和高斯基函数向量，ε为有界偏差.基函数向量φ中的元素φκ可表示为

(18)

其中：κ=1,2,…,n，n为基函数向量的维度，c和σ分别为基函数输入信号的中心向量和宽度.

1.4 基本图论知识

本文采用无向通信拓扑G=(Ω,E,A)描述集群无人机之间的通信关系，其中，Ω={1,2,…,N}为集群无人机集合，E⊆Ω×Ω为机间通信链路集合，A=[aij]N×N为邻接矩阵.如果(UAV#i,UAV#j)∈E，则说明第j架无人机的状态信息可以传输至第i架无人机，同时有aij>0，否则，aij=0.定义第i架无人机的邻近无人机集合为Ni={UAV#j|(UAV#i,UAV#j)∈E}.在集群分布式通信架构中，如果对于任意两架无人机，均存在至少一条通信链路，则认为通信拓扑G=(Ω,E,A)是无向联通图.

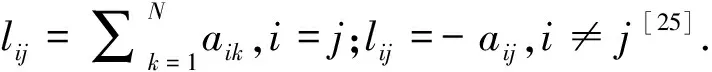
2 强化学习自适应容错协同控制

本节首先构建分布式分数阶同步跟踪偏差，并在此基础上利用神经网络学习机制设计强化学习算法；然后，基于同步跟踪偏差与强化学习算法，设计集群无人机容错协同控制器；最后，利用Lyapunov方法对系统的稳定性进行分析.

2.1 控制目标

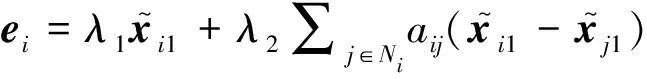
2.2 分数阶跟踪偏差

将式(14)中的xi1进行二次求导，可得：

(19)

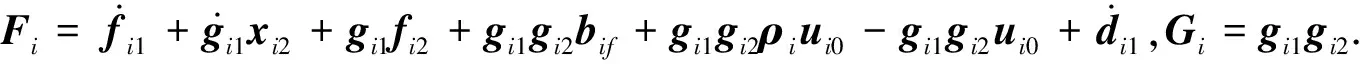
类似文献[26]，定义第i架无人机与近邻无人机的同步跟踪偏差为：

(20)

其中：λ1和λ2分别用于调节第i架无人机的跟踪性能和第i架无人机相对于邻近无人机的同步性能.

基于同步跟踪偏差(20)，设计如下分数阶滑模面：

(21)

其中：λ3和η为正的设计参数，a∈(0,1]为分数阶微积分算子.

对式(21)求导，可得：

(22)

2.3 Actor-Critic神经网络容错协同控制器设计

本小节采用强化学习中的Actor-Critic神经网络机制，设计如下智能自适应容错协同控制信号：

(23)

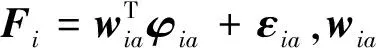
图1 控制结构Fig.1Control structure

将控制信号(23)代入式(22)，则可得：

(24)

借鉴文献[17]，定义如下包含Critic神经网络的Critic函数：

(25)

上述Critic神经网络函数的估计值为：

(26)

设计Actor-Critic神经网络的自适应律如下：

(27)

(28)

其中：κ21、κ22、κ31和κ32为正的设计参数.基于自适应律(27)和(28)，Actor-Critic神经网络组成强化学习单元，并用于调整控制信号(23)的输出.整体控制框图如图1所示.

2.4 稳定性分析

定理1考虑N架固定翼无人机组成的集群编队，假设机间通信链路为无向连通，并且部分无人机遭遇执行器故障，设计同步跟踪偏差(20)、分数阶滑模面(21)、控制信号(23)、Actor-Critic神经网络自适应律(27)～(28)，则所有固定翼无人机均可同步跟踪上参考指令信号xid，并且同步跟踪偏差ei最终一致有界.

证明定义如下Lyapunov函数：

(29)

对上式求导，可得：

(30)

进一步，可得：

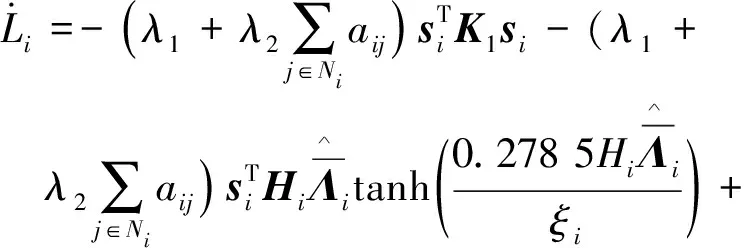
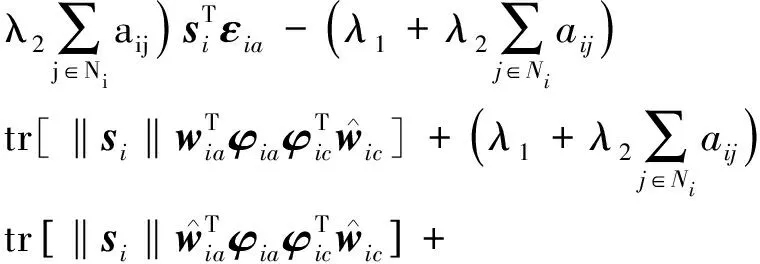
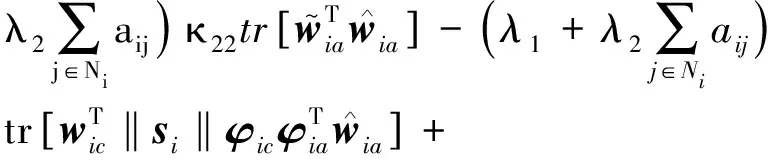
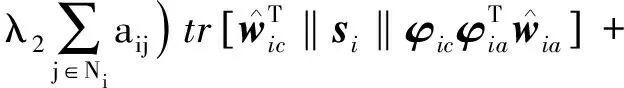
(31)

定义

(32)

则有

T≤‖si‖·‖εia‖+‖si‖·‖wia‖F·

(33)

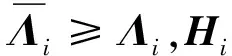
(34)

设计自适应律：

(35)

其中：κ41和κ42是正的参数.

将式(33)、(35)代入公式(31)，可得：

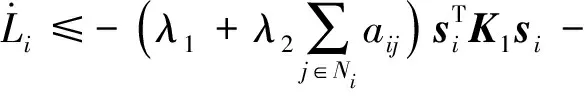
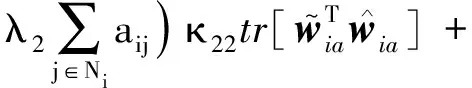
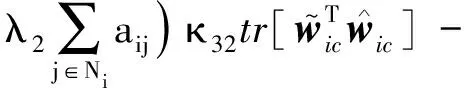
(36)

利用如下不等式：

(37)

可得：

(38)

进一步利用如下不等式：

(39)

(40)

可得：

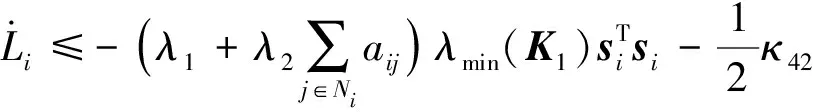
(41)

其中:πi1和πi2的表达式为

(42)

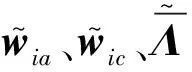
3 仿真分析

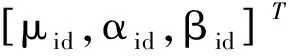
为检验容错协同控制方案的性能，假设UAV#1～UAV#3分别在t=15 s,t=30 s,t=45 s遭遇如下故障：

图2 无人机通信拓扑图Fig.2Communication topology of UAVs

UAV#1副翼、升降舵、方向舵故障(t≥15 s)：

(43)

UAV#2副翼故障(t≥30 s)：

(44)

UAV#3升降舵故障(t≥45 s)：

(45)

无人机的结构参数和气动参数取自文献[29].仿真中的控制参数设为λ1=0.9，λ2=0.2，λ3=1.5，K1=diag{18,27,13}，ξi=0.08，κ21=19.6，κ22=2，κ31=48，κ32=2.7，κ41=98，κ42=2.3.

图3为所有无人机的侧滚角、攻角和侧滑角响应曲线.从图3中可以看出，即使UAV#1～UAV#3在t=15,30,45 s时遭遇执行器故障，但在所设计容错协同控制方案的作用下，所有无人机的姿态均保持有界.图4为所有无人机的角速率响应曲线.从图中可以观察到，当无人机遭遇故障时，角速率信号出现了瞬态变化，但在控制方案的作用下，角速率信号很快稳定下来，从而确保了集群编队系统的稳定性.

图3 无人机姿态角响应曲线Fig.3Time responses UAVs′ attitudes

图4 无人机角速率响应曲线Fig.4Time response of UAVs′ rates

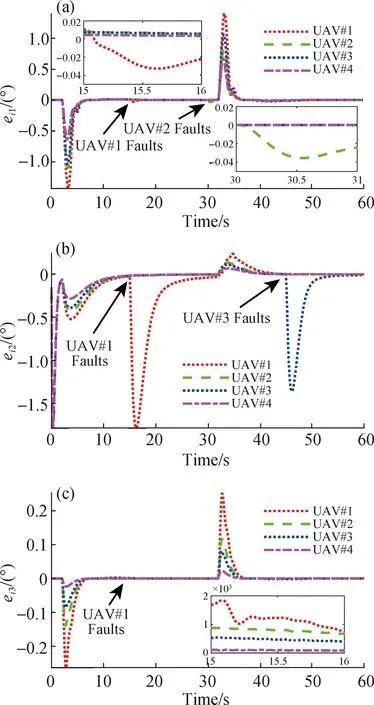
图5 无人机姿态同步跟踪偏差Fig.5Attitude synchronization tracking errors of all UAVs

图6 无人机个体姿态跟踪偏差Fig.6Individual attitude tracking errors of all UAVs

图7 无人机控制输入信号Fig.7Control input signals of all UAVs

4 结 论

本文针对风扰和故障条件下的集群无人机容错控制问题，基于Actor-Critic神经网络强化学习机制，设计了分数阶强化学习容错协同控制方案.首先，构建了可同时反映个体跟踪性能与同步性能的同步跟踪偏差，并引入了分数阶微积分算子，形成分数阶偏差变量；其次，基于Actor神经网络设计了智能自适应容错协同控制信号；再次，设计Actor-Critic神经网络自适应律，激活强化学习算法的学习能力；然后，结合Lyapunov稳定性理论证明所有无人机的姿态同步跟踪偏差均收敛至含零的很小区域内；最后，数值仿真结果验证了所设计的强化学习容错协同控制方案的有效性.