基于强化学习的切换系统综合性能优化设计

孙振东,王苗苗

(1.山东科技大学电气与自动化工程学院，山东青岛266590;2.中国科学院数学与系统科学研究院系统控制重点实验室，北京100190)

切换线性系统由多个线性子系统和一个在子系统间进行切换的监控装置组成.这类系统包含取值于连续空间的系统动态、取值于离散空间的切换动态、及其相互作用，是一类基本而典型的混合动态系统.切换系统为复杂系统建模和控制设计提供了行之有效的体系架构.经过近30年研究，对切换系统的探索已取得巨大进展，包括能控性、能稳性、鲁棒性、适应性等性能[1-5].已有的部分工作表明，切换控制在改进系统暂态性能方面具有巨大潜力[6-7].然而，现有的多数切换设计方法可能引起高频切换或控制信号跃变，损害整体系统的暂态性能，从而限制了切换控制的可应用性.

经典频域方法在工程应用上的一个突出优势是可以对系统的暂态性能进行评估和优化[8].与之相比，基于时域分析的现代控制理论尚缺乏优化复杂系统暂态性能的基本工具.即便对线性系统，针对暂态性能的研究成果还远未完善[9-10]，而对非线性系统超调控制的研究更是凤毛麟角[11-12].利用多模型切换优化系统暂态性能的文献参见文献[13-14].

本文探索连续时间切换线性自治系统的综合性能优化，力图通过有效的切换策略设计实现包括状态模超调，调节时间和指数收敛速率的多目标优化.该多目标优化是建立在整个时间空间的分阶段优化，各阶段的时间窗口依赖于初始条件，因此无法通过预测控制进行滚动式优化.另一方面，优化的变量是切换策略而非传统的控制输入，缺乏基于变分法的最优控制方法.

强化学习是3种基本机器学习范式之一，它关注智能体如何在不确定环境/非平稳过程中采取行动以获得最大奖赏或最小成本[15].对于给定的成本和初态，智能体要寻求适当的行动策略以获取最优的长期(强化)收益[16].切换系统具有多模态切换和清晰的执行-监控双层结构，所以将切换信号构成行动策略空间，利用强化学习对切换规则的优化设计可以探索切换系统的最优控制和最优资源配置等优化问题.但是，对二次型(积分)形式的优化函数，尽管基于自适应动态规划/强化学习的最优控制方法已成功应用于离散时间切换系统的优化设计[17-18]；对连续时间切换系统，由于行动取值于连续空间，难以实现有效搜索[19]，迄今为止，在文献上仍未见强化学习对连续时间切换系统的有效处理.

本文借鉴强化学习的算法思路[20-21]，通过分路径模压缩的设计方法，在无穷的切换策略中汲取有限个行为策略，通过对有限行为策略的串接扩展实现强化信号(系统性能)的迭代优化.选择强化学习方法的优势包括:1) 利用行为→奖赏模式模拟切换逻辑动态与连续动态性能的交互；2) 对切换策略空间进行有效离散化，可在优化目标收敛性和计算复杂度间取得良好平衡；3) 对切换策略的离散化(而不是采样)可避免Zeno现象的发生.由于优化策略是依赖于系统初始状态的，不同初态会对应截然不同的行为动作.本文发展有效结合动态系统分析和策略驱动学习的优化算法，分别给出超调、调节时间和指数收敛率的优化估计.

1 预备知识

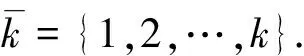
本文考虑不含输入的连续时间切换线性自治系统

(1)

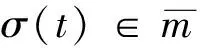
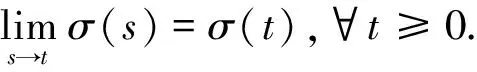
切换路径是定义在有限时间区间的切换信号.设切换路径θ是定义在区间[0，s)上的， 则定义|θ|=s.给定切换路径θ1和θ2，定义其串接(coneatenation)θ1∧θ2为

(θ1∧θ2)(t)=

多个切换路径的串接可类同定义.

设t0，t1，…，tk是切换路径θ的切换时间，则此路径对应的状态转移矩阵为

Φθ=

eAσ(tk)(|θ|-tk)eAσ(tk-1)(tk-tk-1)…eAσ(t1)(t2-t1)eAσ(t0)(t1-t0).

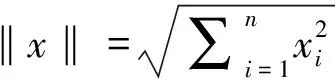
定义1称切换系统(1)为可指数镇定的，若存在正实数α,β及切换信号σ，使得

‖φ(t;0,x0,σ)‖≤βe-αt‖x0‖,

∀x0∈Rn,t≥0.

这里α称为指数收敛率.

引理1[2]切换系统(1)是可指数镇定的充要条件是对任意γ>0,存在有限个切换路径θi，i=1，2,…,l，满足

∀x0∈Rn.

(2)

定义2对切换系统(1)，设初态x0≠0,定义x0对应的(状态模)超调是

注1上述关于系统超调的定义与经典概念有区别：这里考虑的是切换系统在镇定设计基础上的超调量，因此假设状态收敛到原点且初值非零.这实际上结合了经典控制中的超调和欠调概念.显见，若系统可指数镇定，则每个非原点初态对应的超调是有限的.

定义3对切换系统(1)，设初态x0≠0,给定∈(0,1).定义x0对应的-调节时间是

TS(x0,‖x0‖}.

注2可以证明，如果系统可指数镇定，那么对任给正实数，系统具有有限的-调节时间.反之亦然.

2 问题的提出和分解

本文针对切换系统(1)，探索系统综合性能的优化设计，针对给定的系统初态，实现包括超调量、调节时间和指数收敛率的优化计算.为此，作以下假设：

假设1系统(1)可指数镇定.

k=1,2,…,

类似可定义Γ∞.

固定初态x0≠0和≠(0,1).不妨设‖x0‖=1(否则令x0x0/‖x0‖).

考虑到优化目标的基本特征，分3个阶段进行设计.

第一阶段，优化指标为超调，即

这里VEO是VO(x0)的上界估计.

第二阶段，在超调约束下优化调节时间，即

TES=min{|θ|:∃θ∈Γ∞s.t.‖φ(τ;0,x0,

第三阶段，在超调和优化时间约束下优化指数收敛率，即

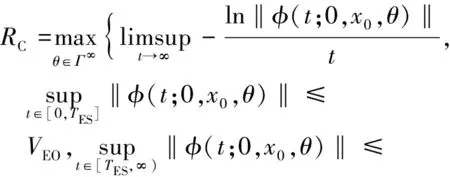
进一步，选取θ(近似)满足上述要求.

完成这3步设计后，切换信号θ即为寻求的优化解.

3 主要结果

3.1 系统分析

记H1为Rn上的单位球面.对任一压缩基路径θi，i=1，2,…,l,定义其对应的单位球上的压缩区域

Ωi={x0∈H1:‖φ(si;0,x0,θi)‖≤γ‖x0‖},

i=1,2,…,l.

进一步，定义

利用S-步骤(S-procedure)技术，可以证明

(3)

其中Vsmin是矩阵的最小奇异值.从计算角度，利用上式通过自适应采样和奇异值分解技术可求得Li.记L=max{L1,L2,…,Ll}.

引理2VO≤L.

证明对任意x0∈H1,利用文献[2]§4.4.1给出的分路径状态反馈切换策略，存在切换路径

θ=θj1∧θj2∧…∈Γ∞,

使得系统轨线φ(t;0，x0，θ)指数收敛.令

ti=|θji|,xi=φ(ti;0,xi-1,θ),i=1,2,….

注意到xi∈Ωji,i=1,2,…，于是有

引理得证.

注3引理2给出系统超调的上界估计.这一估计的精度取决于基压缩路径库的丰度.一般地，系统超调是难以精确求得的.

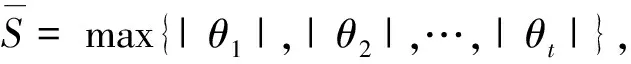
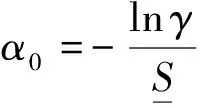
引理3对任意的初态x0，在分路径状态反馈切换策略下有

‖φ(t;0,x0,θ)‖≤β0e-α0t‖x0‖.

(4)

证明在分路径状态反馈切换策略下有

‖φ(|θj1|+|θj2|+…+|θjk|;0,x0,θ)‖≤γk,

k=1,2,….

由此可知

由此可知系统渐近收敛率不小于α0.另一方面，考虑系统在[0,|θj1|)上的动态，设τ满足

eα0τ‖φ(τ;0,x0,θ)‖=

利用轨线端点状态模信息，可得

消去τ，可知

记x1=φ(|θj1|;0,x0,θ)类似可以证明

eα0t‖φ(t;0,x0,θ)‖≤eα0(t-|θj1|)‖φ(t-|θj1|;

0,x1,θ)‖≤β0,t∈[|θj1|,|θj1|+|θj2|).

如此继续下去，引理得证.

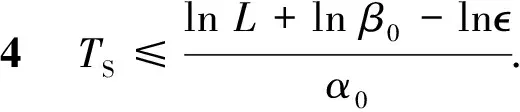
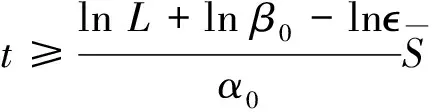
‖φ(t;0,x0,θ)‖≤‖x0‖.

(5)

由定义3，引理得证.

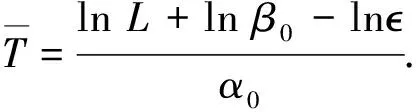
3.2 优化算法

对特定的初态，其对应的超调和调节时间一般远小于系统的超调和调节时间.借鉴强化学习的优化思路，以下分别给出求解超调和调节时间的算法设计.

3.2.1 求解超调估计量VEO的学习算法

第k步：对Λ中每个路径θ，逐一进行以下计算.

2) 判断是否Λ=Ø

(a) 若是，输出VEO,算法结束

注4在此算法中，切换策略库Λ一方面随着k增加进行了更多层的串接，同时又不断被修剪(pruning).数值计算中，系统轨线{φ(t;0,x0,θ):t∈[0,|θ|]}可以用Runge-Kutta四阶法数值求解.由于系统轨线可视作多条局部轨线的联接，其求解可分配到不同的计算步骤中，每步只需保存末端状态值即可.

命题1求解超调估计量VEO的学习算法在有限步结束.

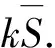
3.2.2 求解调节时间估计量TES的学习算法

第k步：对Λ中每个路径θ，逐一进行以下计算.

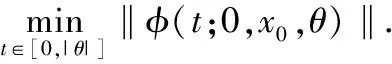
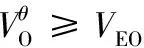
(b) 若否，进一步检查是否VOθ≤L

2) 判断是否Λ=Ø

(a) 若是，输出TES,算法结束

注5容易证明，本算法在有限步结束，给出在超调约束下的调节时间优化估计VEO.

3.2.3 求解收敛速率估计量REC的学习算法

第k步：对Λ中每个路径θ，逐一进行以下计算.

2) 判断是否Λ=Ø

(a) 若是，输出REC算法结束

注6容易证明，本算法在有限步结束，给出在超调和调节时间约束下收敛速率的优化估计REC.

4 仿真例子

考虑带两个子系统的三阶切换系统：

(6)

其中

可以证明，不存在切换路径实现整个状态空间的模压缩[参见文献[22]，Corollary 3.12].另一方面， 取γ=0.95,通过计算可以设计12个切换路径对整个状态空间分段模压缩.进一步，依据引理2和引理4可以分别求出系统超调和调节时间的上界

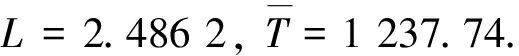
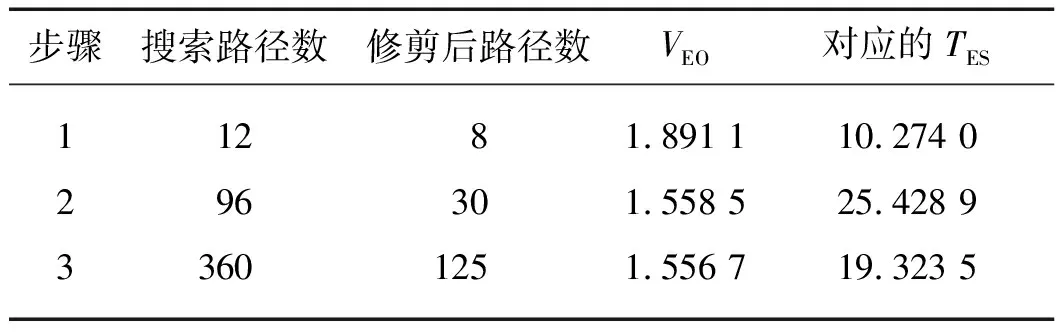
表1 学习算法执行的相关参数

图1是优化后的系统轨线仿真.

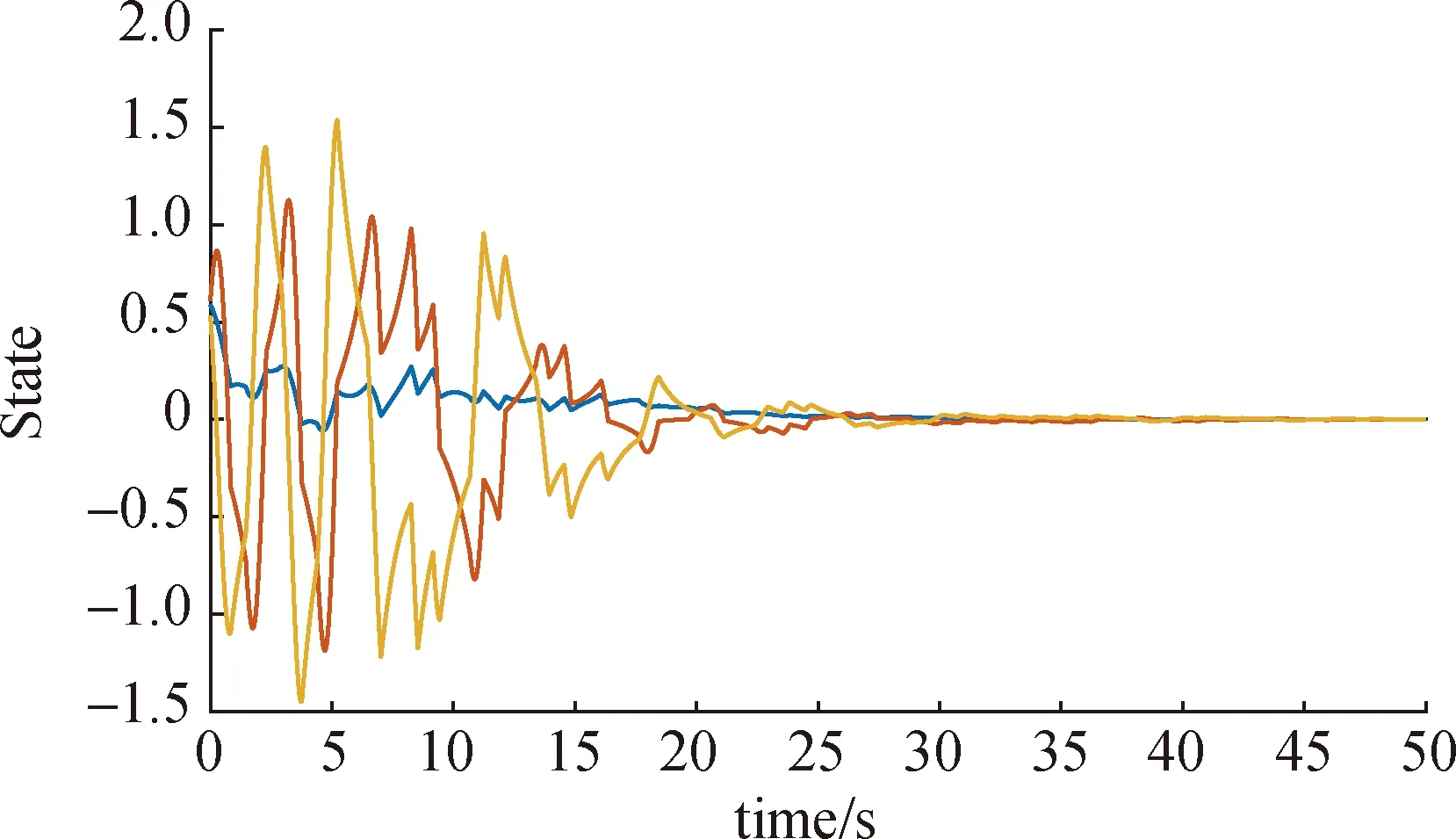
图1 超调优化的系统轨线Fig.1System trajectory for overshoot optimization

进一步，在超调约束下执行求解调节时间估计量TES的学习算法，获得优化的调节时间16.715 5 s.有趣的是，对应的超调为1.243 3,比单纯优化超调得到更优的超调.在此基础上，给定时间区间[0,100],继续优化指数收敛率.图2是整体性能优化后的系统轨线仿真.

图2 整体性能优化的系统轨线Fig.2System trajectory for overall performance optimization

5 结 论

针对连续时间切换线性自治系统，借鉴强化学习思路和分路径模压缩的设计方法，通过对有限行为策略的串接扩展实现系统性能的迭代优化.进一步，发展有效结合动态系统分析和策略驱动学习的优化算法，分别给出超调、调节时间和指数收敛率的优化估计.