基于三层加权分数阶傅里叶变换的安全通信系统*

高 萍，杨宇晓

(南京航空航天大学 航天学院，南京 211106)

0 引 言

随着电子对抗技术的迅速发展，针对飞行器(卫星、飞机)通信信号的射频隐身研究引起了广泛的关注。加权分数阶傅里叶变换(Weighted Fractional Fourier Transform,WFRFT)[1]通过改变通信信号原始调制特征，将私密信号模拟为电磁环境中的公开信号，从而在机理上实现私密通信信号的射频隐身[2]。同时，由于在WFRFT变换域[3]内进行信号处理，截获方难以在传统时频域内解译信号，进一步提高了信号的安全性能。

对于传统的WFRFT通信系统，非合作方在一定时间内可以通过参数扫描[4]获取解调参数，通信信号易被捕获识别[5-6]。文献[7]首先提出了多参数加权分数傅里叶变换(Multiple Parameters Weighted Fractional Fourier Transform，MPWFRFT)的概念。文献[8-9]提出了基于MP-WFRFT的数字通信系统框架，论证了MP-WFRFT信号较于普通的WFRFT信号具有更强的抗截获[10]和抗识别性能，更利于信号的安全传输[11]。文献[12]提出了一种抗截获的大信号掩盖方法，将携带重要信息的弱信号作为大信号的背景信号，实现信号的隐蔽传输。文献[13]提出了一种多层加权分数傅里叶变换，将待调数据等分成多层并行数据，分别进行不同变换阶数的WFRFT，窃听方在未知调制层数和变换阶数的条件下难以正确解调信号，具有较好的保密性能。文献[14]提出了一种双层MP-WFRFT调制方法，破坏了WFRFT的阶数可加性，从而提高了系统的抗参数扫描能力。文献[15]将多层WFRFT与多输入多输出(Multiple-Input Multiple-Output,MIMO)技术相结合，提高了信号的抗截获性能和频谱利用率。但上述研究主要针对多层WFRFT信号的保密性能，未对其调制模拟性能进行讨论。

综上所述，目前针对WFRFT的研究主要集中在单层WFRFT的目标信号调制特征模拟和多层WFRFT的信号加密,而针对多层WFRFT调制的目标信号调制特征模拟的研究还比较少。为此，本文提出了一种基于三层WFRFT的通信信号设计方法，以目标信号星座图特性作为优化目标，采用三层WFRFT调制，选取星座图的裂变点数、裂变构型、裂变样式、模糊程度和旋转角度作为关键参数，选定信号特征约束条件，引入遗传算法进行迭代计算，使得三层WFRFT调制星座图一致且与目标信号调制星座图相同，此时的设计参数为最优控制参数。通过调制星座图仿真、合作方和窃听方的误码率性能仿真，验证了本文方法的有效性和可靠性。

1 三层WFRFT通信系统

1.1 WFRFT调制原理

离散序列X0的WFRFT定义式为

(1)

式中：ωl为加权系数，l=0,1,2,3。ωl是α和V的函数，其定义如式(2)所示：

(2)

式中：M为加权项数；α为变换阶数；V=[MV,NV]表示尺度向量，MV=(m0,m1,m2,m3)，NV=(n0,n1,n2,n3)。

WFRFT定义式中的离散余弦变换(Discrete Fourier Transform,DFT)矩阵F如下式所示：

(3)

式中：N为序列X0的长度；λN=exp(-i2π/N)。

由上述内容可知，WFRFT变换域调制的控制参数包括变换阶数α和尺度向量V，通过设计上述参数可实现信号调制特征的改变。

1.2 基于三层WFRFT的通信系统

基于三层WFRFT的通信系统框图如图1所示，基本流程为：在发射端，将初始数据进行QPSK基带映射，然后按照前后顺序将数据等分为三层并行数据，三层数据分别进行参数集为(α1,V1)的WFRFT、(α2,V2)的WFRFT、(α3,V3)的WFRFT调制，再将三层数据按照顺序进行并串转换，形成的串行数据再经过成形滤波、D/A转换、上变频处理后发射到信道中；在接收端，经过信道的数据通过下变频、A/D转换、匹配滤波处理后，再按照前后顺序等分为三层并行数据，三层数据分别进行参数集为(-α1,V1)的WFRFT、(-α2,V2)的WFRFT、(-α3,V3)的WFRFT调制，即三层加权分数阶傅里叶逆变换，经过并串转换后对数据进行QPSK基带逆映射，得到最终恢复数据。

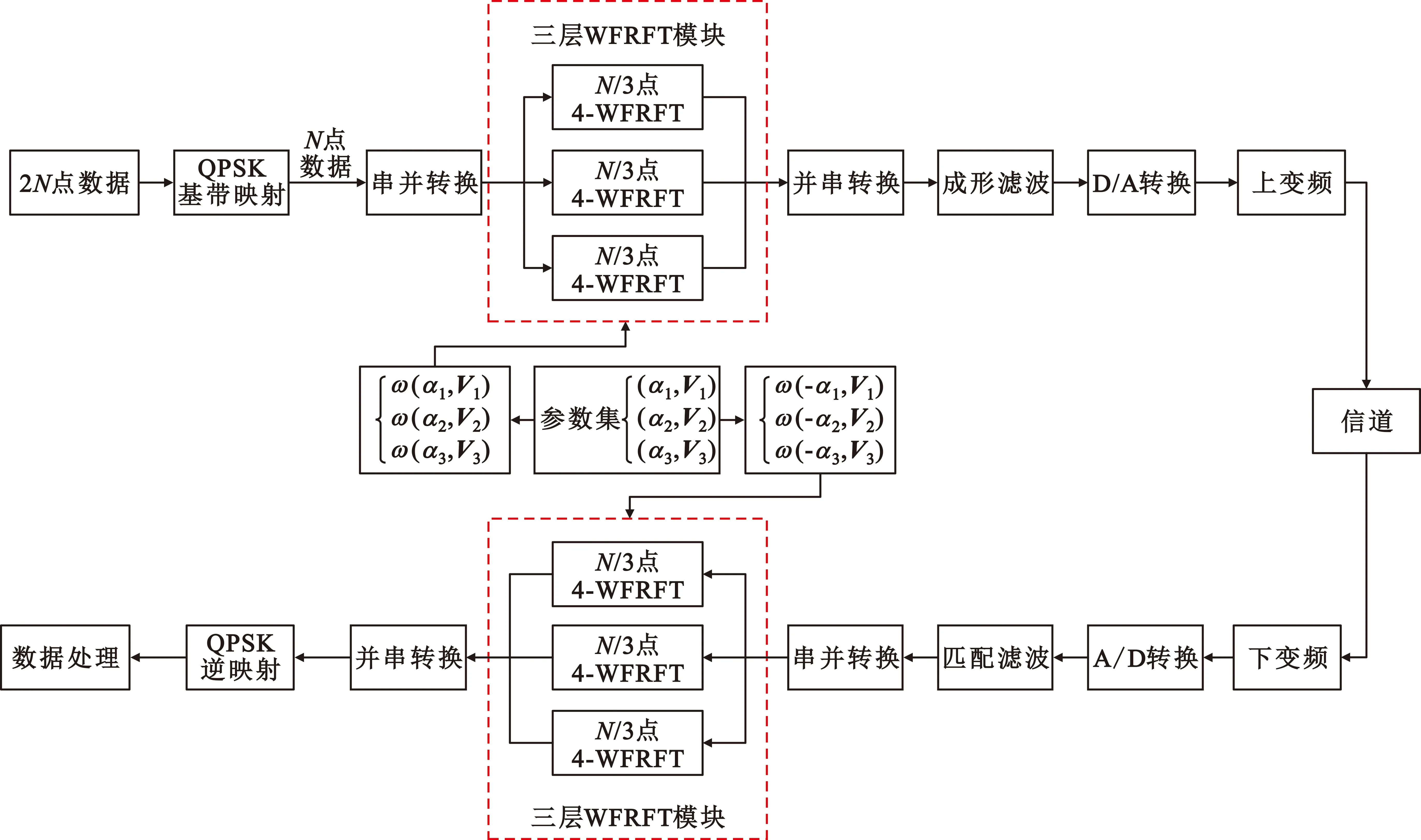
图1 基于三层WFRFT的通信系统框图

2 三层WFRFT调制信号模拟

WFRFT调制通过改变原始信号的调制特征，将私密信号模拟为电磁环境中的公开信号，从机理上实现私密通信信号的射频隐身；通过改变调制参数使得每一层WFRFT的调制特征都一致且与目标信号调制特征相同。因此，首先需要分析目标信号的关键特征，再根据与特性相关的关键参数来约束调制信号的星座图特征。本节将针对星座图裂变点数、星座图裂变构型、裂变样式、模糊程度和旋转角度等关键特征进行分析。

2.1 目标信号关键特性

(1)星座图裂变点数

为实现信号调制特征的变化，首先需要确定所需的信号星座图裂变点数。基带信号的调制阶数B是决定星座图最多裂变点数的关键参数。

以常见的2PSK信号、16QAM信号为例进行星座裂变点数的仿真，星座图如图2所示。图2(a)将2PSK信号的2个星座点分裂成4个，图2(b)将16QAM信号的16个星座点分裂成256个,因此，若原始信号为B进制的基带调制，则调制信号可裂变为B2个星座点。

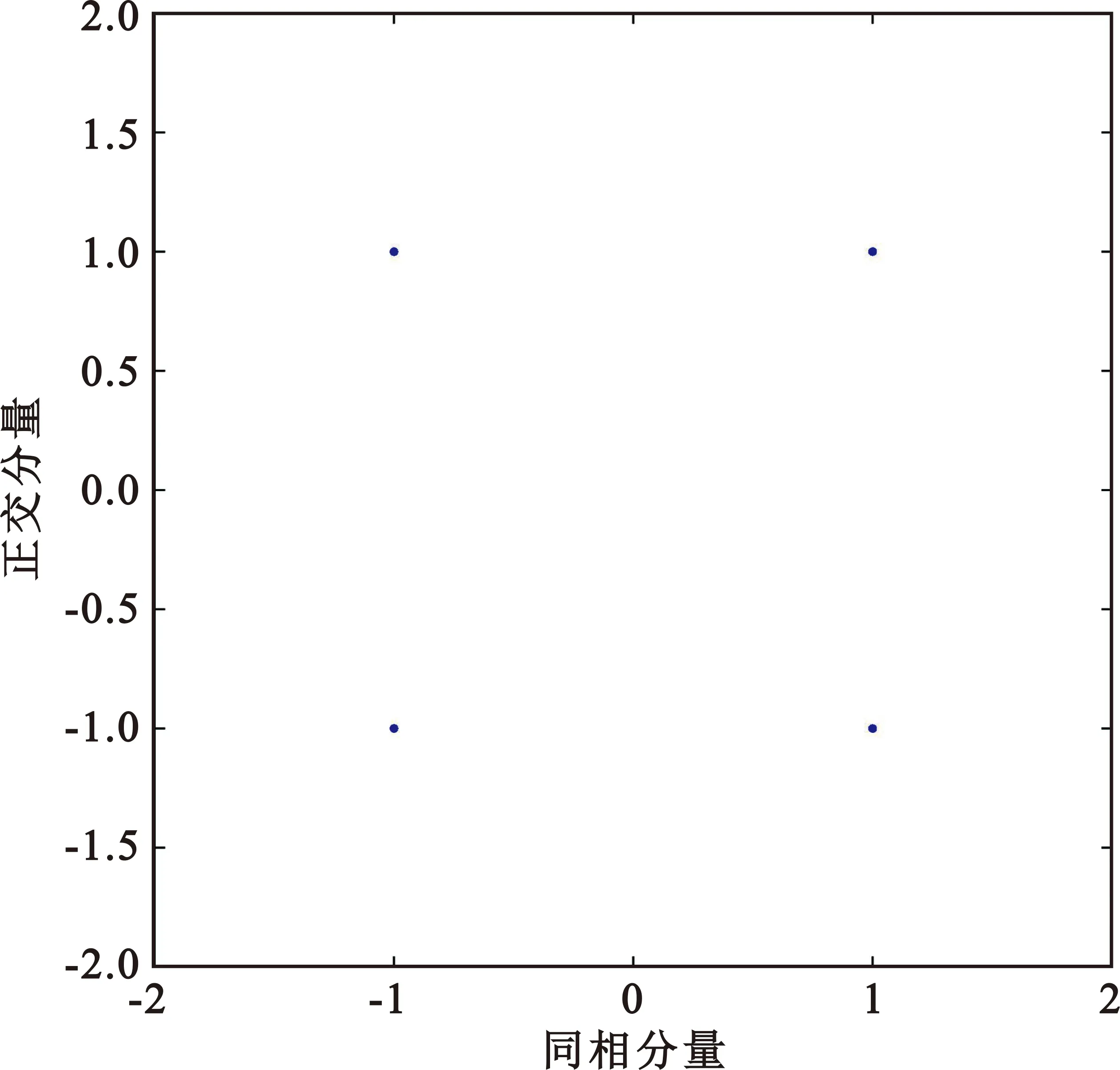
(a)2PSK裂变星座图(B=2)

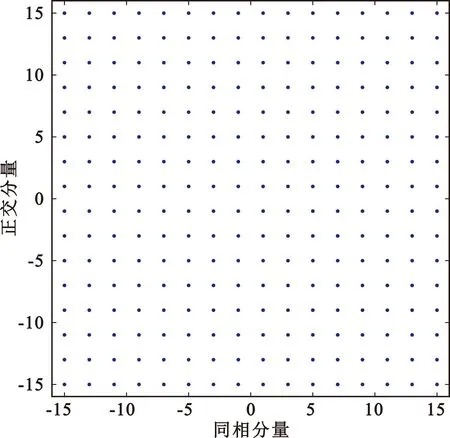
(b)16QAM裂变星座图(B=16)

(2)星座图裂变构型

X0和X2分别为原信号项与反转信号项，星座图都呈现出原QPSK映射的星座特征形式，故处理信号星座图中出现的旋转、模糊现象与这两项没有关联，这两项仅表示时域部分，而相应分裂特性的产生是对应时域分量项的叠加，因此星座图的裂变特性主要是由原始序列X0及其反转序列X2所决定的。因此，定义WFRFT裂变函数如下式所示：

(4)

以ω0和ω2作为基准参考点，由几何知识可知，两者的角度直接影响了星座点的分布及形状，当ω0⊥ω2时，星座裂变构型具有矩形特性。因此，ω0和ω2的夹角〈ω0,ω2〉是决定星座图裂变构型的关键参数。

(3)星座图裂变样式

由裂变函数可得，序列和被加权后，星座点会发生分裂和旋转，而旋转幅度大小和星座点聚散程度与ω0、ω2之比有关，当模值比例因子η=|ω0|/|ω2|取值为0.5时，WFRFT调制信号的星座图为均匀分布的16个点簇。

(4)星座图模糊程度

矩阵满足线性变换的特性，而随机变量序列的分布渐近于正态分布。当多种(7种以上)随机变量的分布特性相同时，它们通过线性组合形成的随机变量就具有了类高斯分布的特性，所以加权之后的X1、X3决定了WFRFT信号的星座模糊特性。则WFRFT模糊函数如下式所示：

(5)

由上式可知，调制信号星座图的模糊程度本质是X1、X3加权求和的结果，通过调节参量|ω1|2+|ω3|2，可将调制信号设计为不同信噪比条件下的信号特征，从而模拟特定的信道条件。

(5)星座图旋转角度

三层WFRFT叠加信号调制特征接近目标信号需要每层WFRFT调制星座图与目标信号星座图相近，除了裂变构型、裂变样式、模糊程度等条件外，还要求每层WFRFT的星座图旋转角度满足一定条件。星座图旋转角度公式如下：

(6)

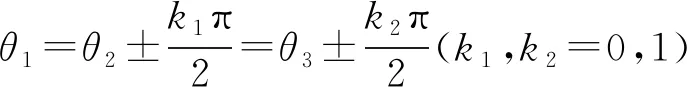
综上所述，三层WFRFT调制实现目标信号调制特征模拟的关键参数如表1所示。

表1 信号模拟关键参数

为了验证本节所提三层WFRFT信号调制特征模拟方法的有效性和可行性，以QPSK信号作为原始信号，进行目标信号调制特征的模拟实验。

2.2 三层WFRFT系统参数设计

(1)目标信号调制特征选取

本节以标准16QAM信号调制特征作为待模拟的目标信号特征，信号星座图如图3所示。

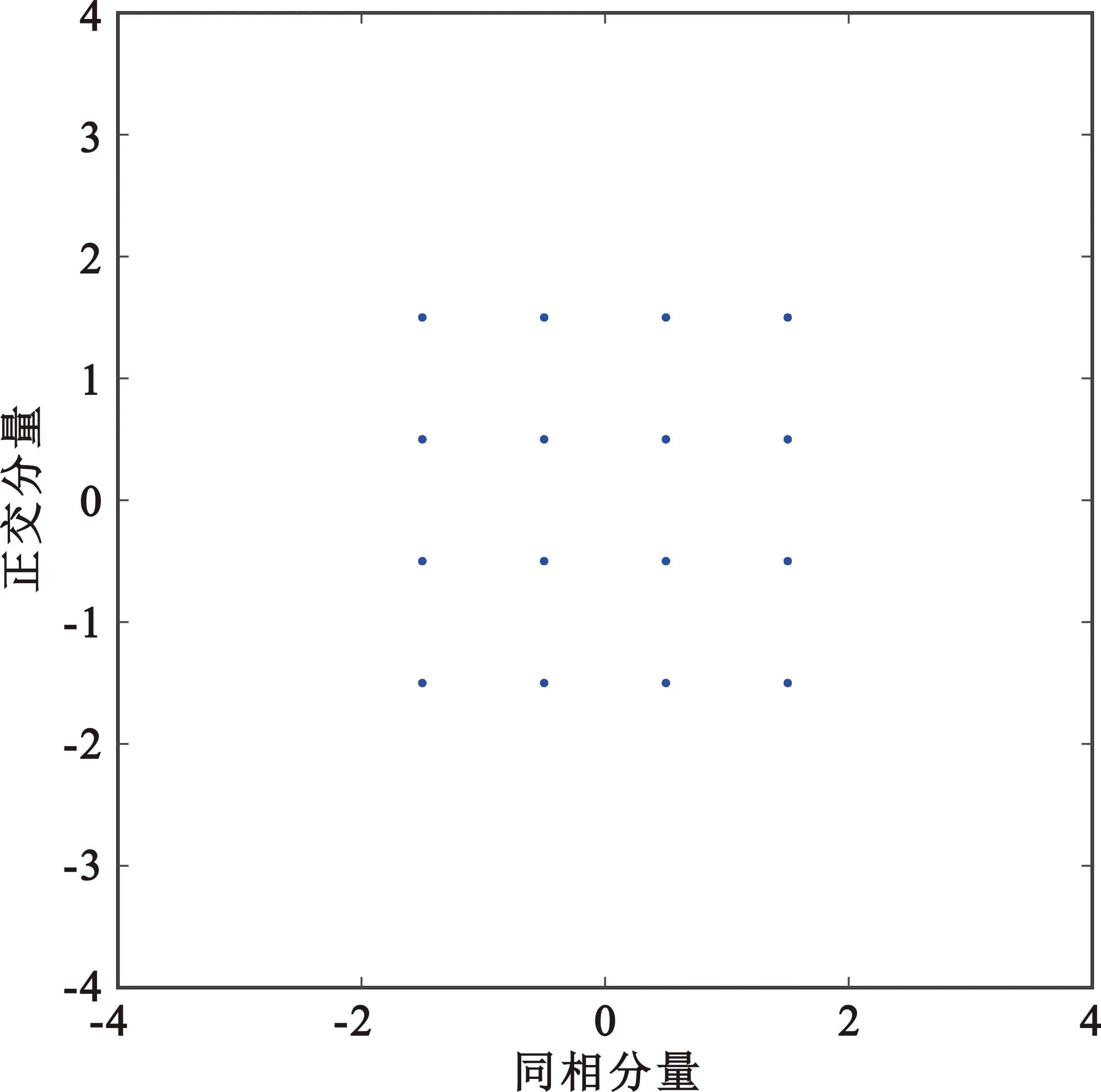
图3 目标信号星座图

(2)优化模型约束条件设置

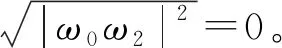
③根据WFRFT的周期为4这一特性，将调制参数α1、α2、α3的取值范围都设置为[0,4)。

④尺度向量V为非负整数且上界P设置为10。

⑤目标信号星座图为清晰的16个点，故调制信号的模糊分量应尽可能小，即|ω1|2+|ω3|2的取值趋向于0。

⑥目标信号星座图为标准16QAM信号星座图，当星座图旋转角度为0、π/2、-π/2时星座图特征仍然保持不变，故三层WFRFT调制星座图的旋转角度θ取值为±kπ/2(k=0,1)。

2.2.1 优化模型

根据上一节的目标信号调制特征选取和控制参数的设置，构建三层WFRFT系统优化目标函数如下：

minf(α,V)=f1(α1,V1)+f2(α2,V2)+f3(α3,V3)，

其中，f1(α1,V1)、f2(α2,V2)、f3(α3,V3)分别为三层WFRFT的优化目标函数;η=0.5;l≠2;k=0,1。

在此基础上，构建三层WFRFT系统的优化模型如下：

minf(α,V)=f1(α1,V1)+f2(α2,V2)+f3(α3,V3)

s.t.

l=0,1,2,3;

V=[MV,NV];

MV=[m0,m1,m2,m3],NV=[n0,n1,n2,n3];

mk,nk∈[0,10],k=0,1,2,3;

α1,α2,α3∈[0,4);

θ1=θ2=θ3=0。

2.2.2 遗传算法

针对上述优化模型，引入遗传算法进行迭代优化计算，得到三层WFRFT信号调制特征模拟的最优控制参数集如表2所示。

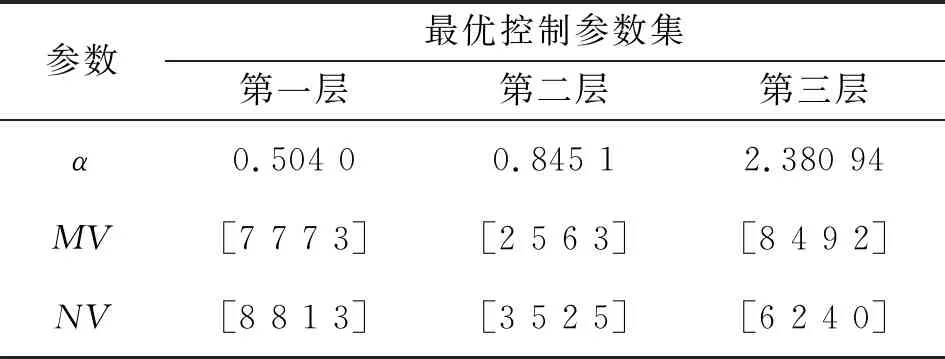
表2 最优控制参数

3 仿真测试与性能分析

为了验证本文所提三层WFRFT系统的通信性能、模拟性能和保密性能，对上述系统进行仿真验证。系统解调所需先验参数为调制层数、变换阶数α1、α2、α3和尺度向量V1、V2、V3。

3.1 三层WFRFT系统通信性能

将本文所提三层WFRFT系统在高斯信道下的误码进行100次仿真计算取其平均值，得到平均误码率，并与QPSK理论误码率进行对比，结果如图4所示。

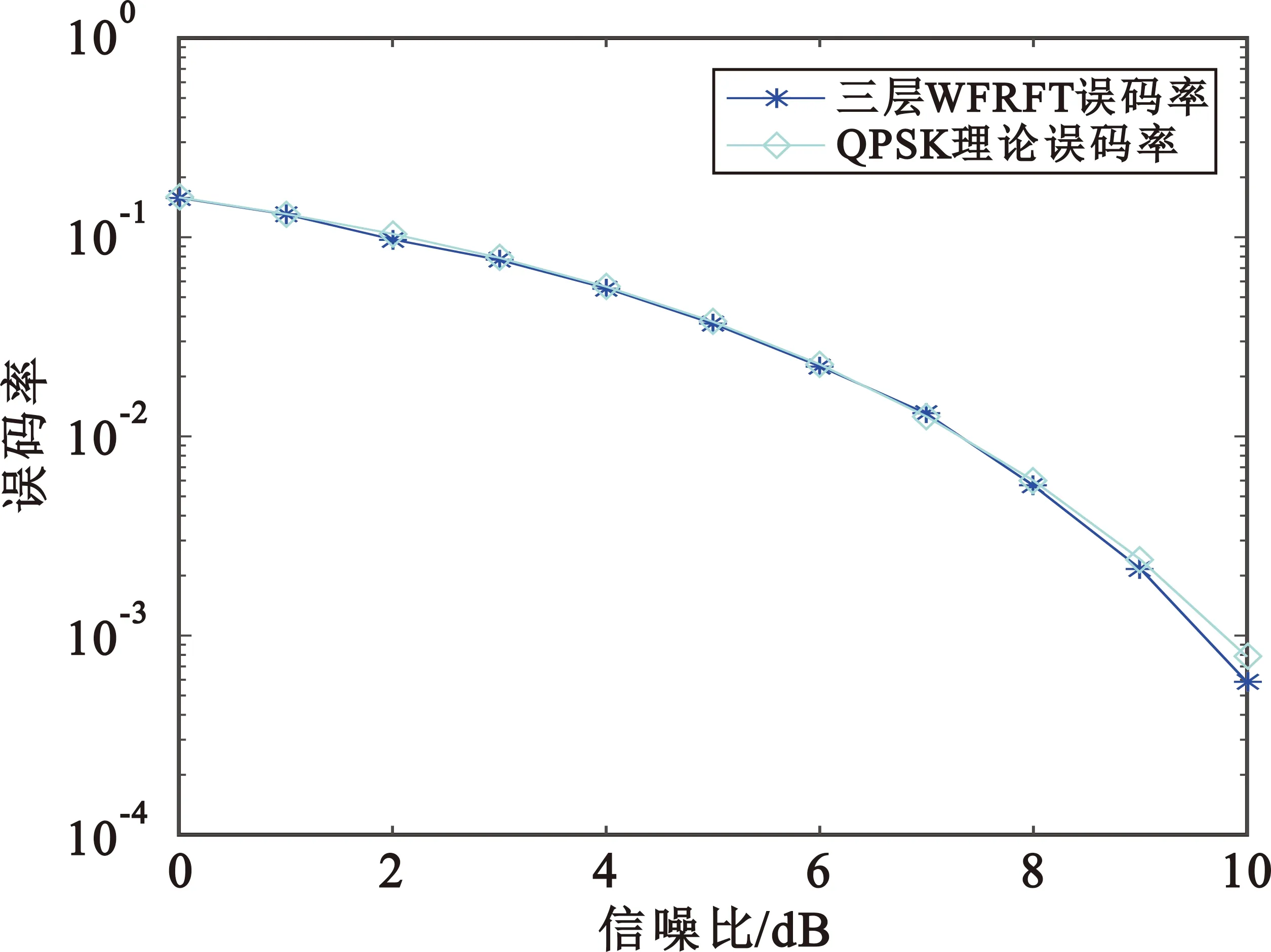
图4 系统通信性能分析

由仿真结果可知，合法接收方在高斯信道中的误码率曲线与QPSK理论误码率曲线相近，在相同的信噪比下误码率没有明显提高，故三层WFRFT系统具有较好的通信性能，满足基本通信需求。

3.2 三层WFRFT系统模拟性能

采用表2最优控制参数集进行三层WFRFT调制，信号星座图仿真结果如图5所示。对比图5(b)和图5(f)可知，三层WFRFT调制信号星座图构型、样式、模糊程度和旋转角度均符合目标信号调制特征，达到了目标信号模拟的预期效果。

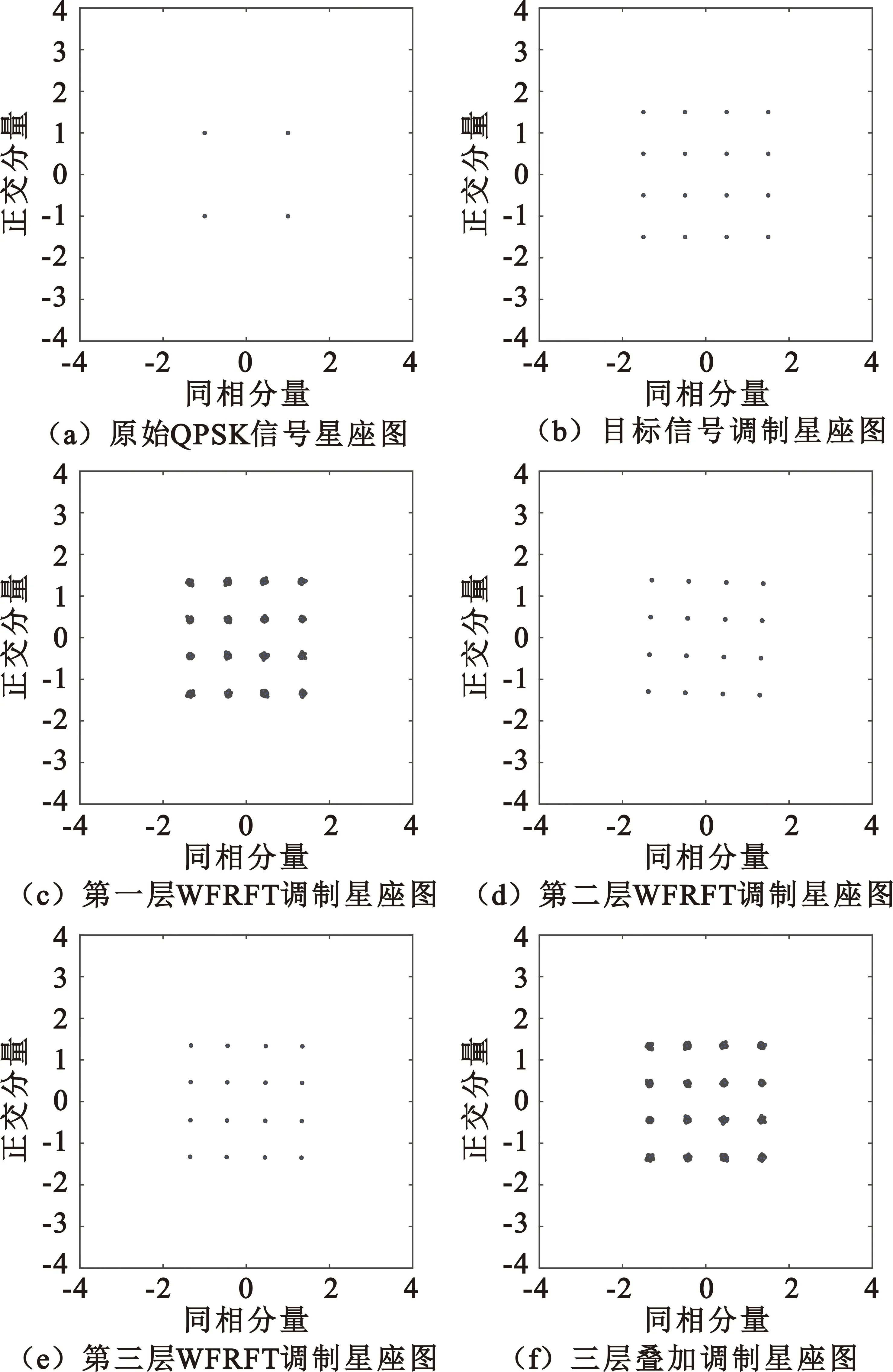
图5 三层WFRFT信号调制星座图

3.3 三层WFRFT系统保密性能

非合作方在未知调制层数、变换阶数和尺度向量的条件下与合作方误码率曲线对比如图6所示。

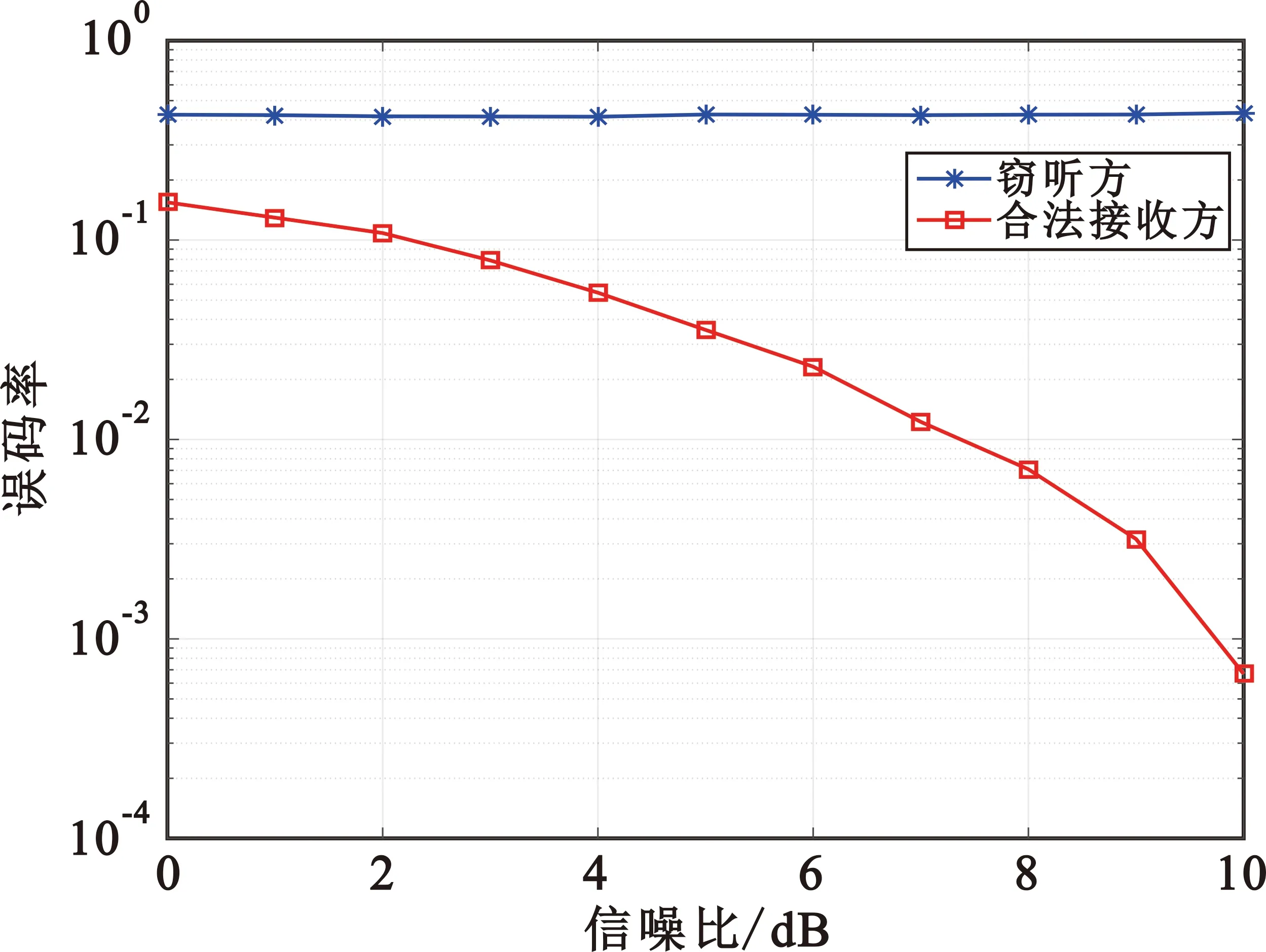
图6 窃听方未知任何先验参数的误码率曲线

由仿真结果可知，非合作方在未知调制层数、变换阶数和尺度向量的条件下基本无法正确解调信号。

3.3.1 三层单参数WFRFT系统保密性能仿真

当参数集(α,V)中V=0时，WFRFT调制参数仅有变换阶数α，系统为三层单参数WFRFT系统。在该系统中，若非合作方已掌握调制层数为三层且调制方式为4-WFRFT，但所掌握的变换阶数数值有误差，误码率曲线如图7所示。

图7 三层单参数WFRFT系统中α抗扫描特性

由仿真结果可知，随着窃听方掌握的变换阶数α的误差从0.1递增到1，非合作方解调误码率也是依次递增的，并且在相同信噪比下高于合法接收方的误码率。当α的误差大于或等于0.5时，非合作方几乎无法正确解调信号。

3.3.2 三层多参数WFRFT系统保密性能仿真

在三层多参数WFRFT系统中，非合作方已知调制层数和调制方式，掌握的变换阶数α和尺度向量V有误差时，误码率曲线如图8所示。其中，图8(a)为非合作方掌握变换阶数α的误差分别为0.01、0.001、0.000 1时的误码率曲线，图8(b)为窃听方掌握尺度向量V的误差分别为1、2、3时的误码率曲线。

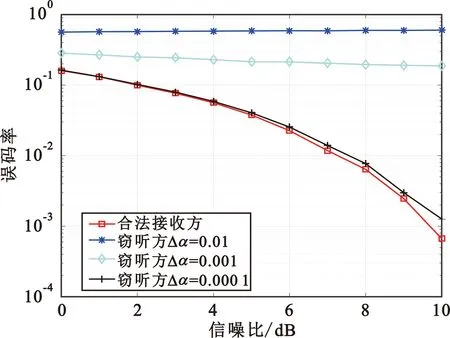
(a)三层多参数WFRFT系统中α抗扫描特性

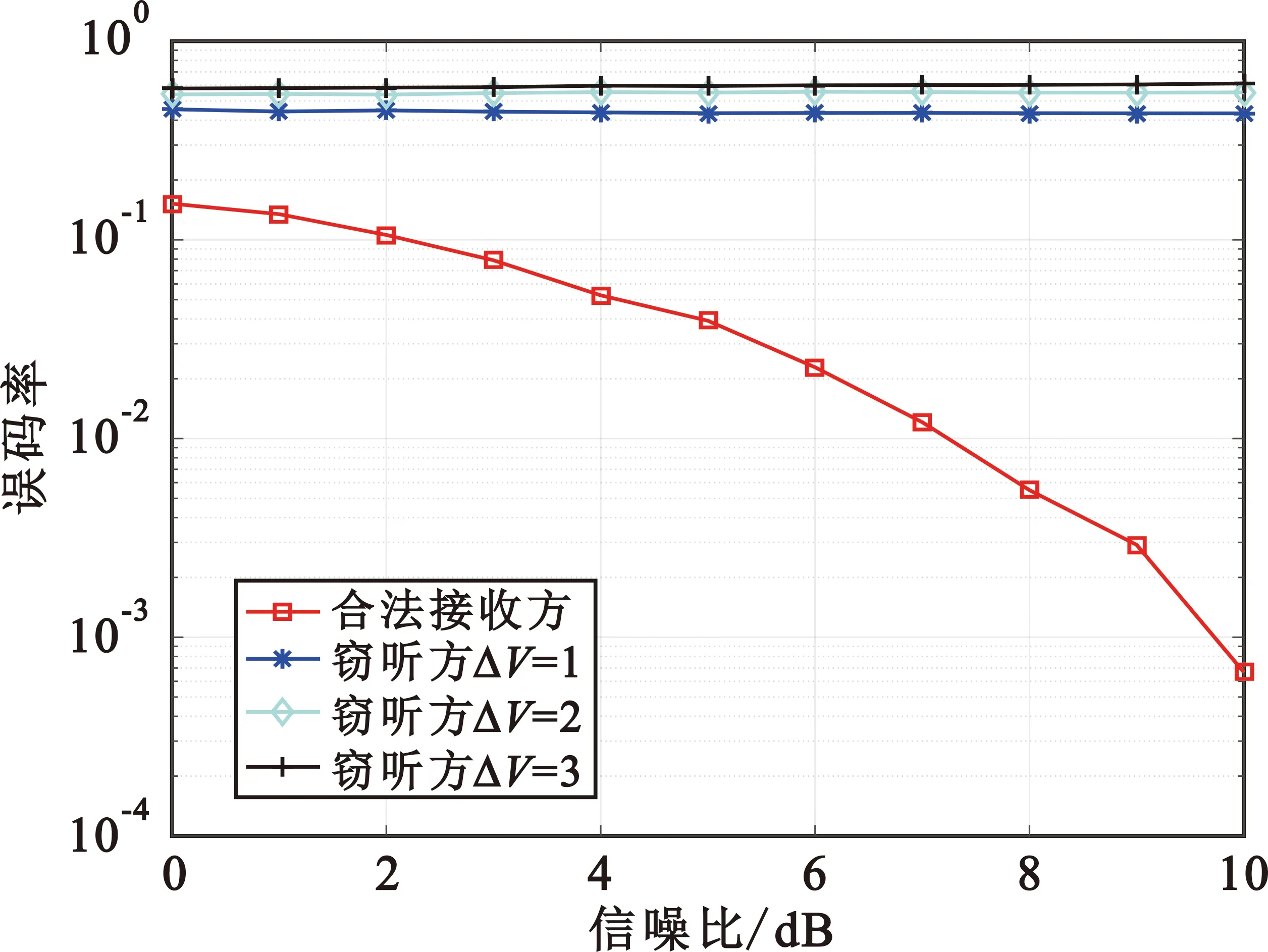
(b)三层多参数WFRFT系统V抗扫描特性图8 三层多参数WFRFT系统α、V抗扫描特性

由图8(a)可知，非合作方若要正确截获参数信息，对变换阶数α的扫描间隔应该小于0.000 1。以0.000 1为标准进行计算，在变换阶数α的全周期内，非合作方需检测4/0.000 1次，即40 000次。由于三层多参数WFRFT由三层MP-WFRFT组成，故非合作方通过参数扫描的方式获取解调参数，需对三层多参数WFRFT信号进行三次MP-WFRFT扫描，若采用相同的扫描间隔0.000 1，三层多参数WFRFT信号扫描次数应为MP-WFRFT信号扫描次数的立方倍，非合作方对三层多参数WFRFT信号的扫描次数为40 0003=6.4×1013次，扫描次数的增加导致非合作方付出的代价增加，由此说明三层多参数WFRFT安全通信系统具有较强的抗截获性能。将图8(a)与图7相比可知，与三层单参数WFRFT系统相比，三层多参数WFRFT系统变换阶数α的误差对解调误码率的影响更大。由图8(b)可知，非合作方掌握尺度向量V的误差为1、2、3时，非合作方误码率均大于0.5，无法正确解调信号。

综上所述，基于三层加权分数阶傅里叶变换的安全通信系统具有良好的抗参数扫描特性，保密性强。

4 结束语

本文提出了一种基于三层WFRFT的通信信号设计方法，将传统单层WFRFT扩展为三层结构，每层进行不同调制参数的WFRFT调制，非合作方在未知调制层数的情况下无法正确分层解调，调制参数也由9个增加到27个，增大了非合作方参数扫描的难度，相比于传统单层WFRFT系统具有更好的保密性能。另外，调制参数的选择以目标信号星座图作为优化目标，选取与目标信号特性相关的关键参数，确定信号特征设计的约束条件，引入遗传算法迭代计算，得到目标信号模拟的最优控制参数。星座图仿真结果表明，本文所提方法可以实现目标信号星座图特征模拟，符合预期模拟效果。误码率仿真结果表明，合作方解调误码率曲线接近QPSK理论误码率曲线，说明系统能够满足基本通信需求；在相同的信噪比条件下，非合作方解调误码率远大于合作方，几乎无法正确解调信号，说明系统具有较好的保密性能。因此，本文所提三层WFRFT系统具有良好的模拟性能、通信性能和保密性能，验证了本文所提方法的有效性。

为了进一步提高系统的保密性能，后续可将三层WFRFT系统的加权分数傅里叶变换项数扩展到多项，从而进一步增加系统的先验参数，提升复杂度，使其具有更好的抗截获识别功能。