融合后验概率和密度的不平衡数据欠采样方法

任艳平，郑 重，江一飞，严远亭，张燕平

安徽大学 计算机科学与技术学院，合肥 230601

近年来，随着机器学习和数据挖掘等技术快速发展，越来越多的机器学习算法从学术界走向工业界。然而这一过程也面临许多实际问题的挑战。数据不平衡问题就是一个典型的例子。对一个二分类问题，样本数量相对较少称为少数类，样本数量较多的称为多数类。数据的不平衡分布对传统机器学习方法提出了挑战，这些算法在构建和训练模型时都有一个基本假设：类间样本呈均匀分布。将这些算法直接用于不平衡数据时，最终得到的结果往往不是很理想。这是因为以最小化总体误差为学习目标的传统分类算法会忽视少数类而过多地关注多数类。但在很多实际应用场景中少数类更值得关注。如医学诊断[1]、欺诈检测[2]、破产预测[3]、文本识别[4]、漏油检测[5]等。

针对不平衡数据的学习问题，学者们从不同角度提出了大量解决方法，这些方法大致可以分为三类：数据层面的方法[6-8]、算法层面的方法[9-10]和集成方法[11]。数据层面的方法通过对不平衡数据重采样，使不平衡的样本分布变得相对平衡，从而提高分类器对少数类的识别率。重采样包括过采样、欠采样和混合采样。算法层面方法通过修改现有算法或提出新算法来解决类不平衡问题。如代价敏感方法，对不同的类别分配不同的误分类代价，通常赋予少数类样本更高的误分类代价，从而增强分类器对少数类样本的识别能力。集成方法通常结合前面两类方法构建多个学习器，并采用集成策略将这些学习器组合成一个多分类系统，以此来提升模型的分类性能[12-13]。数据层面的方法是目前解决类不平衡问题的主流方法，它的主要优势在于其实现简单且能够直接应用于传统机器学习算法。

过采样和欠采样是目前使用最多的两种数据层面的方法。过采样方法主要通过生成合成新样本来平衡数据分布。其典型代表有SMOTE[14]、Borderline-SMOTE[15]、ADASYN[16]等。但是如何合理地生成新样本避免引入额外异常样本和可能的过拟合问题仍然是过采样的一大难点[17]。欠采样方法则是通过选取多数类样本的子集来缓解类别不平衡现象。相较于过采样而言，欠采样方法训练时间更少，训练过程中采用的数据都是来自原数据集中的样本，使得模型更加真实可靠[18]。当前关于欠采样的研究大多认为不适当的样本选择策略所导致的关键样本的信息丢失是影响欠采样方法性能的主要原因，为此，研究者从不同角度提出了一系列的针对性的方法[19-22]。

与此同时，近年来有研究[23-25]表明，相较于类别不平衡，数据复杂因子如类重叠、子概念、噪声等对不平衡学习的性能具有更为直接和重要的影响。已有一些研究表明，高效地处理类别重叠能够有效提升过采样方法的性能[26-27]。但是，对欠采样方法中处理类别重叠的相关研究并不多见。欠采样处理重叠问题主要是为了避免选择高重叠的样本。过采样方法处理重叠问题主要是避免生成的样本进一步造成重叠，加重采样之后的重叠程度。这两种方法处理类别重叠的目的都是为了使平衡后的数据集中的样本重叠度低，它们的区别主要在于实现途径不同。为此，本文针对欠采样过程中的类重叠问题，提出了一种基于后验概率和分布密度的欠采样（BPDDUS）方法。该方法的主要思路是先通过样本的近邻信息，实现重叠区域样本的检测并提出了相应的重叠样本清洗策略，其次通过样本的分布信息对清洗后的样本进行欠采样，提升不平衡学习的性能。本文的主要贡献如下：

（1）提出了一种能够有效处理类别重叠的欠采样方法。该方法提出了一种基于贝叶斯后验概率的先清洗后欠采样的策略。

（2）提出一种融合多数类全局密度信息和局部分布信息的样本选择方法，引入集成学习强化不平衡学习的性能。

（3）在43个不平衡数据集上和13种采样方法的对比实验，验证了本文所提的考虑避免重叠的欠采样思路的有效性。

1 相关工作

自SMOTE被提出以来，不平衡数据学习受到广泛关注，涌现了大量基于SMOTE的衍生算法。如Han等人[15]提出的专注处于边界区域的少数类样本的Borderline-SMOTE策略；He等人[16]提出的专注于困难样本的ADASYN策略；Bunkhumpornpat等人[28]提出的专注于安全区域样本的Safe-Level-SMOTE策略；以及结合聚类技术来避免采样过程中生成噪声样本或重叠样本的LR-SMOTE[29]、GDDSYN[30]方法；引入过滤或清洗技术的混合采样方法SMOTE-IPF[31]、SMOTE-Tomek和SMOTE-ENN[32]等。

与过采样策略相对应的方法为欠采样方法，它包括随机欠采样和有监督欠采样。随机欠采样方法（RUS）是从多数类中随机抽样，被选中的样本将被删除直到数据集达到平衡为止。然而，该方法未考虑数据的实际分布情况，采样具有随机性，容易丢失样本的重要信息。有监督欠采样方法则需要预先设定好选择标准，有目的地删除多数类样本来平衡数据分布。如何根据不平衡数据的分布信息选取多数类样本来构建分类决策面成为此类方法的研究重点。

近年来，研究者们提出了许多智能的欠采样方法。Wilson[33]提出的ENN根据K近邻分类原则将错分的多数类删除，但由于大部分多数类样本的局部区域分布的样本多为同类样本，导致ENN所能删除的样本十分有限。Ivan[34]提出的Tomek Links通过清洗数据来降低类间重叠，其主要思路是找到两个类标签不同且最近邻互为对方的样本，然后移除属于多数类的样本或两者。Hart[19]提出使用1-NN的方法压缩多数类的CNN方法。此外，Mani等人[35]提出了Near Miss利用多数类和少数类之间的距离关系剔除多数类样本的一类方法。Smith等人[23]提出IHT方法，它是在训练数据集上应用分类器，然后筛选掉概率低于阈值的多数类样本。

然而，上述方法大多都是基于近邻信息和随机欠采样的简单规则，在处理复杂的数据时得到的分类效果往往不佳。基于聚类策略的欠采样方法主要利用K-means算法将训练数据集划分为多个簇，然后从这些簇中挑选信息多数类样本子集。如Lin等人[20]介绍了两种聚类欠采样策略。该方法先将所有的多数类样本聚类为与少数类样本等量的簇，然后提出利用簇中心来表示多数类和使用簇中心的最近邻样本代表多数类的两种样本选择策略。然而，基于K-means的聚类方法容易受到噪声和离群点的影响，当数据分布比较复杂时，这类方法并不可靠。

近年来，集成技术在欠采样中得到了广泛的应用，相关研究[13，36]表明欠采样算法更适用于构建集成学习分类系统。基于集成的欠采样方法通过在多个欠采样数据集上训练一组分类器，能够在一定程度上减少多数类样本的信息丢失问题，提高模型性能。集成欠采样方法的典型代表有Seiffert等人[11]提出的RUSBoost及Liu等人[13]提出的EasyEnsemble和BalanceCascade等。

此外，现有研究表明当数据样本单纯在数量上不平衡时并不意味着这个数据就难以分类，而是在不平衡之外的其他因素[37]，比如噪声、离群点、类重叠等也会影响模型的分类性能，而类的不平衡会进一步加剧这一问题。为此，出现一些针对不平衡数据中类重叠问题的相关研究[38-39]。

2 融合后验概率和密度的不平衡数据欠采样方法

本章主要介绍基于贝叶斯后验概率的欠采样方法BPDDUS。BPDDUS的工作原理主要由以下三部分组成：首先，清洗多数类中的噪声和重叠样本；然后，对处理后的多数类样本分配权重；最后，根据多数类样本的采样权重随机采样并构造多个基分类器，集成训练。

为描述方便，这里先给出一些形式化的描述：Dtrain=Dmaj∪Dmin，Dtrain表示给定的不平衡训练集，Dmaj表示多数类样本集，Dmin表示少数类样本集。N=Nmaj+Nmin，N为训练集样本数量，Nmaj为多数类样本数量，Nmin为少数类样本数量。X∈Dtrain∧X=(x1,x2,…,xm)，X表示一个m维的样本，xi表示样本的第i个特征值。Y={y1,y2}，Y表示样本的标签，其中y1为多数类标签，y2为少数类标签。

2.1 多数类样本的清洗

对重叠区域的多数类样本进行处理能够有效提升不平衡数据的分类效果，本文提出的方法通过对样本局部信息学习，根据样本局部分布特征对多数类样本进行清洗，避免选择的多数类样本子集中还存在高重叠样本。目前，挖掘局部信息的方法有很多，最经典的是基于KNN的方法，已经广泛应用于许多学习算法中，比如SMOTE、MWMOTE等。

此外，分类决策实质上是通过将待识别样本的特征空间划分成多个决策区域，然后根据样本的特征向量位于哪个决策区域来判断它属于哪一类别。贝叶斯决策论是概率框架下实施决策的基本方法。对分类任务来说，在所有相关概念都已知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记[40]。在这里，利用贝叶斯后验概率的KNN估计来获取多数类样本的局部信息，并依据样本的局部信息来识别多数类样本中的噪声、重叠样本以及信息样本。其中，贝叶斯后验概率的K近邻估计公式如下：

其中，BPi表示待测样本Xi属于Y的概率，K表示Xi的最近邻样本数量，NK_Y表示Xi的K个近邻中同类样本的数量。基于式（1）来计算训练集中每个多数类样本属于多数类的后验概率，得到式（2），且Xi∈Dmaj，1≤i≤Nmaj。

本文提出的方法首先利用式（2）计算每个多数类样本属于多数类的后验概率，然后根据概率值大小筛选信息多数类样本。

从总体上来看，随着BPi的增大，样本的安全水平也在增大。然而，对于BPi＜1 2的样本，它们的重叠程度较高，周围分布了较多的异类样本。这些样本大概率为噪声或重叠样本，对后续的模型训练会产生不利影响。相反，对于BPi≥1 2的样本，这些样本是靠近决策边界或位于多数类样本的密集区域或边缘区域的信息样本，相对比较安全。尤其是那些靠近边界的边缘样本，它们携带了分类的重要信息，这类样本有助于提升模型的分类性能。为了增强分类边界的可分性，提升后续不平衡数据的学习性能，将BPi＜1 2的多数类的采样权重设置为0，以避免噪声样本或高度重叠区域中的多数类样本参与后续的模型训练。

如图1，圆圈表示多数类样本，四角星表示少数类样本。为了更好地描述多数类样本的局部情况，以图1（a）～（b）中多数类样本A、B、C分别描述噪声样本、重叠样本以及信息样本（最近邻数量为5）。其中，图1（a）中样本A深入少数类内部，其周围分布的全为少数类样本，后验概率BPA=0；图1（b）中的样本B靠近少数类群，其后验概率BPB=2 5，这类样本的类别不确定性最大，不仅会影响其周围少数类样本的识别，还会模糊类决策边界，增加类不平衡问题的学习难度。图1（c）中的样本C远离少数类群，其后验概率BPC=1，这类样本对于不平衡数据的分类模型有着重要的作用。

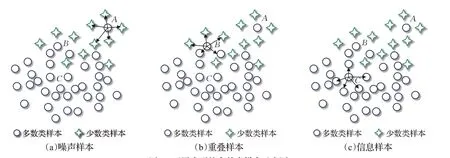
图1 不同类型的多数类样本示意图Fig.1 Different types of majority samples in imbalanced data

2.2 多数类样本的加权

在2.1节中，本文利用贝叶斯后验概率的K近邻估计剔除不平衡训练集中潜在的噪声点和重叠度较高的多数类样本，如图2（a）黑色实心圆为被剔除的样本，空心圆为信息样本。接下来，将对剩余的信息多数类样本做进一步分析，根据不平衡数据的分布特征来评估不同样本对分类的重要程度并依此为其分配相应的采样权重。

根据信息多数类样本在输入空间的初始分布情况可以把样本划分为三种类型：第一种为靠近分类边界的边缘样本，即内边缘样本；第二种为处于多数类内部区域的高密度样本，即中间样本；第三种为远离分类决策边界、远离中间样本的外边缘样本。如图2（b），黄色实心圆为内边缘样本，红色实心圆为中间样本，蓝色实心圆为外边缘样本。在这三类样本中，中间样本的密度最大，内边缘样本和外边缘样本的密度相对较小。另外，远离边界的中间样本和外边缘样本冗余度较大，能够提供的信息比较有限，它们所携带的信息分类器可以从其他样本中获得。相比之下，内边缘样本能够提供更多的有用信息，对提升模型的学习性能有着重要的作用。如果仅考虑样本的密度进行采样，那么中间样本就会采得多，其他样本少。虽然当前已有基于密度的采样方法[30]，但是单用密度在某些情况下并不能很好地度量样本之间的差异性。如图2（b）中的Part1和Part2区域中的样本，这些样本的密度虽然相同，但是它们距离分类决策面的距离是不一样的。Part2区域中的样本比Part1区域中的样本距离决策面更近，对分类的贡献程度更大，得到的采样权应该更大。因此，为了更好地度量样本对不平衡学习的重要程度，引入了信息熵来进一步刻画样本之间的差异。其中，样本离分类决策面越近，熵值就越大。综合考虑样本的全局密度和样本的信息熵来评估样本对分类的重要性。这里给出以下公式来计算样本的全局密度、信息熵以及多数类样本的采样权重：

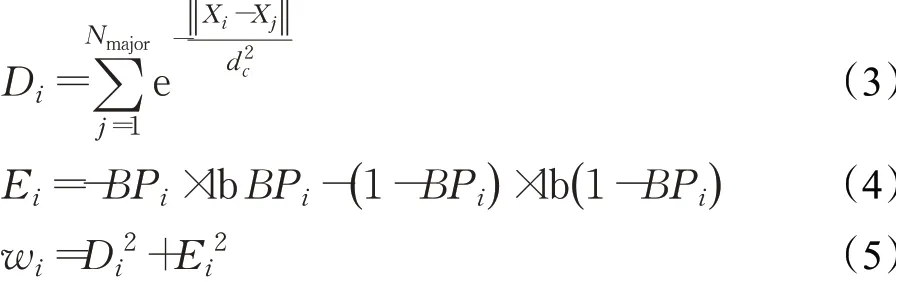
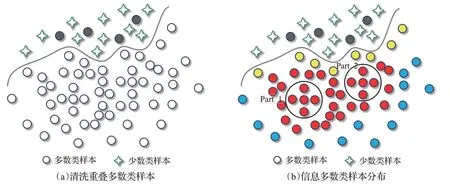
图2 信息多数类样本的空间分布图Fig.2 Spatial distribution of informative majority samples

式（3）为基于高斯核的全局密度计算公式，∀Xi,Xj∈Dmaj，i≠j，Di表示样本Xi的全局密度，dc表示截断距离表示样本Xi和Xj之间的欧氏距离，ω为比例因子。式（4）为伯努利分布熵计算公式，Ei表示多数类样本的信息熵值。式（5）为样本的权重wi计算公式。为了消除量纲的影响，在获得样本的采样权重后对其进行规范化处理。

2.3 集成学习模型的构建

通过2.1节和2.2节对训练数据集进行预处理并按采样权重无放回地随机抽取Nmin个信息多数类样本，结合少数类样本以获取一个平衡分布的数据集。这虽然在一定程度上能够减少关键多数类样本的信息丢失，但若数据中少数类的绝对数量很少时，欠采样很容易由于训练数据不足，出现欠拟合现象，导致分类性能变差，同时样本的信息丢失问题仍无法有效解决。为此，集成学习策略被广泛应用于不平衡数据集的欠采样中，通过构建集成学习系统能够有效地缓解多数类样本的信息丢失问题，同时提升后续模型的泛化能力。

本文结合加权随机采样和并行集成方法来构造不平衡数据的集成分类学习模型。其中，并行集成方法的主要原理是利用不同基分类器之间的差异性，通过各分类器的投票结果来降低分类错误。具体实现过程如下：

（1）构建单个基分类器：对多数类样本按权重无放回地随机抽取与少数类等量的样本，并结合所有少数类样本构建基分类器。

（2）形成集成学习系统：对训练集重复执行步骤（1）来构建一组基分类器，并将获取的基分类器用于bagging集成学习。

（3）结合所有基分类器的预测值，由相对多数投票决定最终的分类结果。

本文方法先通过贝叶斯后验概率来清洗重叠样本，然后根据全局分布密度和信息熵为信息样本设置权重，并依此按权随机欠采样，最后构建集成学习系统.算法的具体步骤如下：

算法1融合后验概率和密度的不平衡数据欠采样方法（BPDDUS）

输入：不平衡训练集Dtrain，近邻数量K，比例因子ω，基分类器数T。

3 实验设计与分析

为了验证所提算法的有效性，本文采用KEEL数据库（http：//www.keel.es）中的二分类不平衡数据集进行对比实验。

3.1 数据集

本文基于KEEL数据集库中的100个不平衡数据集进行实验研究。考虑到KEEL中的一些数据集都是来自同一原始数据的分解变换，为此对数据集进行了筛选。首先，选择所有未重复的数据集；然后，对于重复的数据集选择不平衡率最高和次高的数据集；最后，对剩余的数据集，选择少数类样本数量少于10个的数据集。通过上述的方法得到43个数据集。表1给出了选定数据集的详细信息。其中，IR表示数据的不平衡率，OR表示类间的重叠程度[41]，m表示样本的属性个数，N表示训练集样本的数量，Nmaj表示多数类样本的数量，Nmin表示少数类样本的数量。数据集按IR从小到大排列，这些数据集的IR范围为1.86～129.44，OR范围为0～0.99。

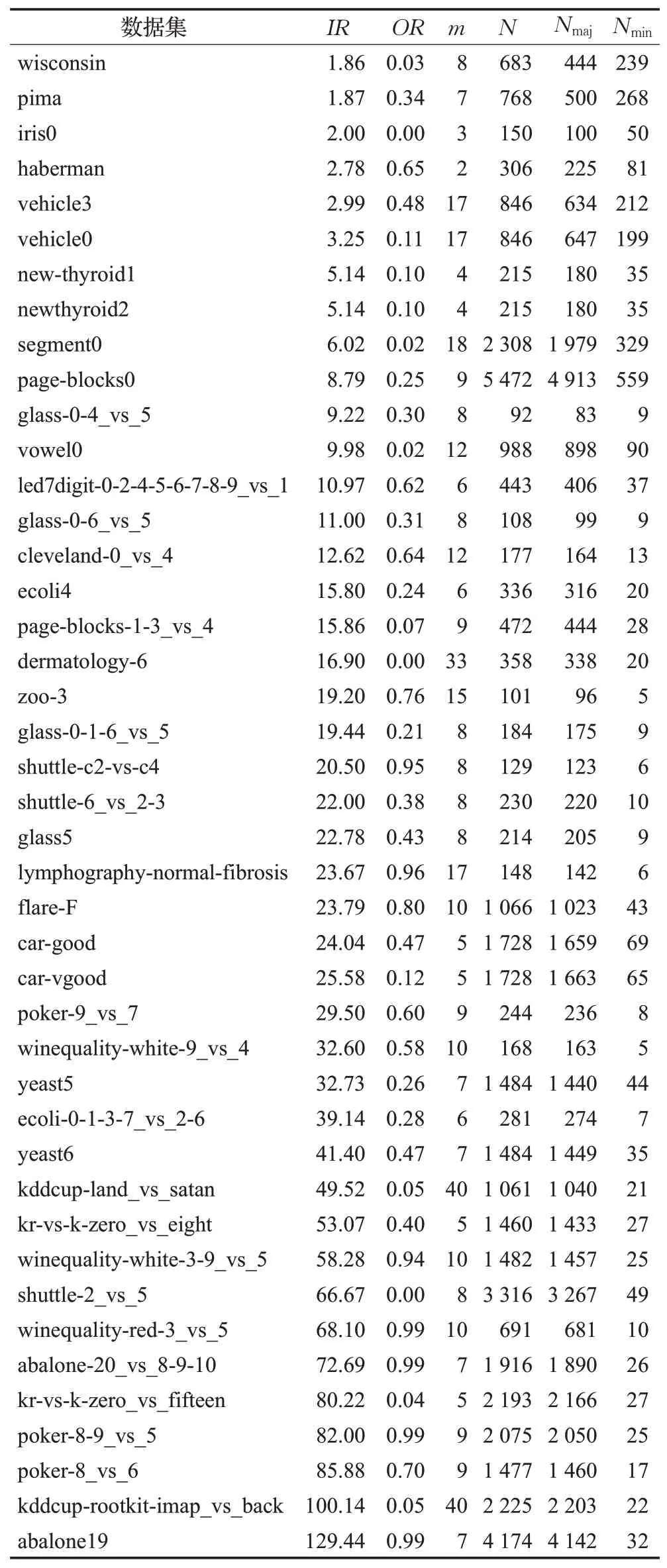
表1 43个KEEL数据集的详细信息Table 1 Details of 43 KEEL datasets

3.2 性能指标

目前比较常用的分类器的评价指标主要有准确率（Accuracy）、精确率（Precision）、召回率（Recall）、F1-score、G-mean以及AUC。其中，准确率为分类正确的样本占总体样本的百分比，它是分类问题中最简单、直观的评估指标，但存在着明显的缺陷。当处理不平衡数据的问题时，准确率不能客观评价学习算法的好坏；Precision又称查准率，针对样本最终的分类结果而言，在所有被分类为少数类的样本中实际为少数类的样本的概率，表示对少数类样本的预测准确程度；Recall又叫查全率，针对实际样本而言，在实际为少数类的样本中被分类为少数类样本的概率。F1-score是Precision和Recall的加权调和平均值，是Precision和Recall的综合指标，F1-score越高，学习模型就越稳健；G-mean是反映了分类器对整体分类性能的评估指标，只有当少数类和多数类的识别率都比较高时，G-mean就较高；AUC则是ROC曲线[42]下的面积，AUC值越大，模型的分类效果越好。因此，本文以AUC、G-mean和F1-score作为性能的评估指标。

3.3 参数分析

BPDDUS算法主要参数：（1）K用于挖掘多数类样本局部信息的最近邻数量；（2）ω用于计算多数类样本全局密度的比例因子；（3）T集成训练的基分类器数量。对于KNN近邻估计K参数，如果取值过小容易产生方差较大的估计，然而K值过大则会产生偏移估计，所以在这里将K设置与SMOTE算法中近邻参数相同，即K=5。在本节中进行了两组实验分别研究ω和T对BPDDUS算法的分类性能影响，由于高斯径向基核函数具有较强的局部性，参数ω决定了该函数的作用范围，随着ω的增大其局部感知能力会减弱。在这里，将ω的域值设定在[1%，2%，3%，4%，5%]。为了节省空间，从表1中随机选取5个IR不同级别的数据集替代选定的所有数据集进行实验，它们分别为wisconsin、flare-F、yeast6、poker-8_vs_6和abalone19，对应的IR分别为1.86、23.79、41.40、85.88、129.44。如表2为不同ω下BPDDUS在三个指标下的性能值。

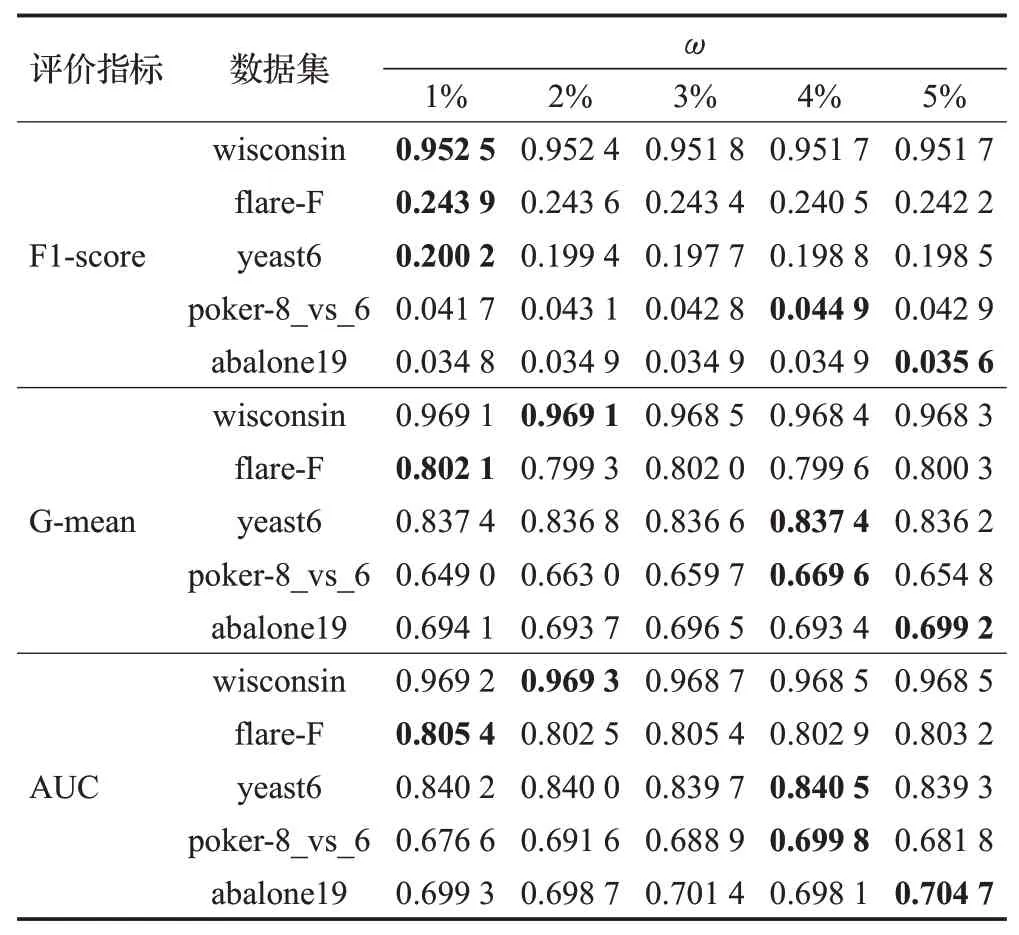
表2 不同ω下BPDDUS的性能值Table 2 Performance values of different ω on BPDDUS

根据表2中的对比结果可知：（1）同一数据集在不同ω下BPDDUS的性能差距不明显，说明BPDDUS算法对参数ω的敏感度比较小，分类性能比较稳定。（2）较小的数据集在ω为1%～2%分类效果相对更好，较大的数据集在ω为4%～5%效果更好。对于集成训练参T，研究T分别在[1，5，10，20，30，40，50]下与BPDDUS算法性能的关系。如图3为BPDDUS随T的改变下的AUC值。从图中可以看出，随着T的增大，模型的分类性能逐渐升高，特别是在基分类器从1～5时效果明显。同时，对IR较小的数据集wisconsin，T值的改变对BPDDUS算法性能变化不明显，而对IR较大的数据集poker-8_vs_6和abalone19在T由1增大到20这一阶段，BPDDUS算法性能提升比较明显，在T为30～50时BPDDUS在这5个数据集上的性能较稳定。从上述实验结果可以进一步说明集成学习的重要性，对于不平衡率较高的数据集，可以通过增加基础学习器来提升模型的分类性能。

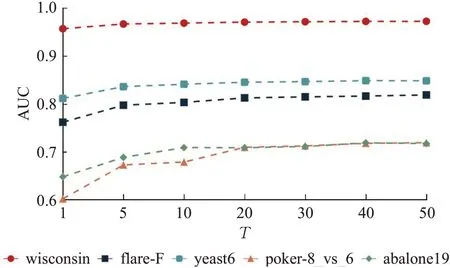
图3 不同T下BPDDUS的AUC值Fig.3 AUC values of BPDDUS at different T values

3.4 结果分析

为了防止在训练过程中出现过拟合问题，同时确保训练集和测试集的类间比例与原始数据一致，本文采用5折分层交叉验证法进行实验。每次实验运行10次，实验结果取10次5交叉的AUC、G-mean和F1-score均值以避免实验的随机性对结果产生影响。本文将BPDDUS（简写为BPUS）算法与13种采样方法进行比较，分别为：ClusterCentroids（CC）、NearMiss（NM）、ENN、TomekLinks（TL）、SMOTE+Tomek（ST）、SMOTE-IPF（SI）、RUS、EasyEnsemble（EE）、RUSBoost（RB）、CNN、AdaCost（AC）、IHT、RBU。这13种算法均来源于imblearn库。为了保证实验的公正性，所有实验均以CART决策树为基分类器，对比算法的所有参数均为默认参数。

同时，为了更直观地分析实验结果，将BPUS与不同算法在43个不平衡数据集上的AUC、G-mean和F1-score的对比结果整理为图4～6。图中深蓝色的部分“DN+”表示在当前性能指标上，BPUS性能值大于其他对比方法的数据集数量，浅蓝色部分“DN=”表示BPUS与其他方法的性能值相同的数据集数量，黄色部分“DN-”表示其他方法性能值大于BPUS的数据集数量。从图4和图5可以看出在指标AUC、G-mean上BPUS与其他方法相比至少有20个数据集表现更优，尤其是与CC、NM、RUS、RBU相比本文的BPUS算法优势更加明显。由图6可知，本文所提方法尽管在F1-score上超过了5种算法，但整体而言，相对表现不佳。尤其是和SMOTE+Tomek、SMOTE-IPF的表现差距较大，这一结果与文献[18]的结果一致，其可能的原因是：一方面过采样方法能够提供更多的安全样本和更低比例的危险样本；另一方面，当数据集中少数类样本较少时，在交叉验证的训练过程中训练集由于缺乏少数类数据的支撑，而导致对少数类样本的识别精度偏低，这可能是另一个方面的原因。

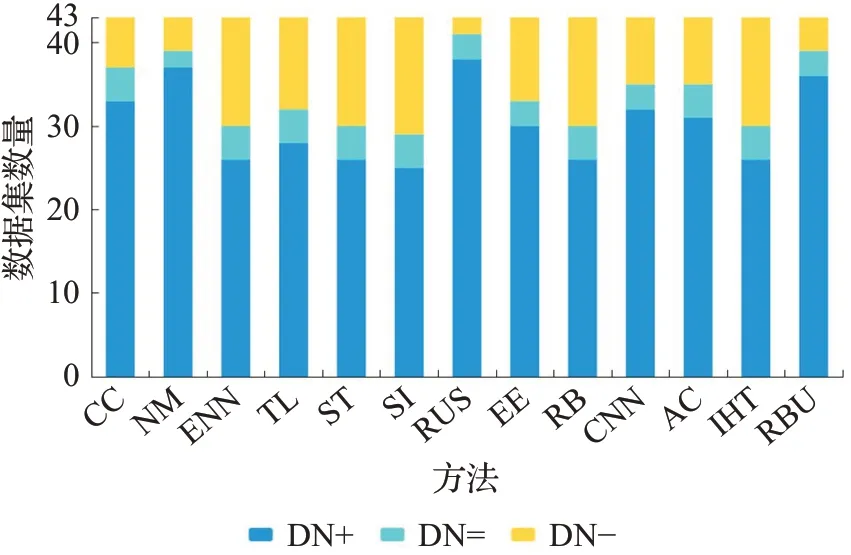
图4 对比实验指标AUC结果Fig.4 AUC results of comparative experiment

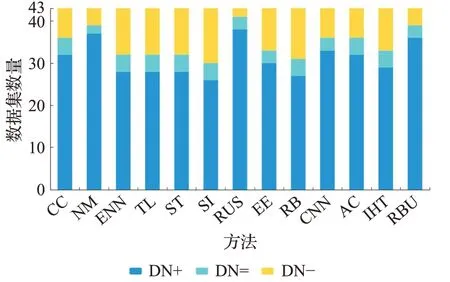
图5 对比实验指标G-mean结果Fig.5 G-mean results of comparative experiment

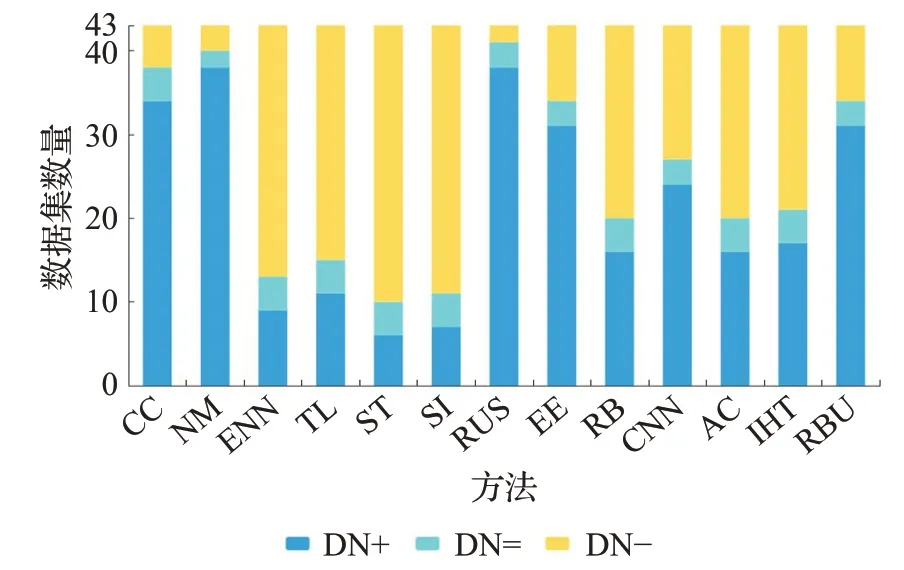
图6 对比实验指标F1-score结果Fig.6 F1-score results of comparative experiment

为了进一步验证BPUS算法的有效性，本文对上述13种对比算法和BPUS算法进行无参的显著性统计假设检验，在这里使用双因素秩方差分析（Friedman检验），表3为所有算法在选定的不平衡数据集上Friedman检验的统计量结果，其显著性水平α=0.05，检验服从统计量为22.36，FF(1 3,546)为1.74。从表中可以看出AUC、G-mean和F1-score下和FF均大于和FF(1 3,546)，p值远远小于0.05，这说明在0.05的水平上应该拒绝原假设，认为这14种算法的分类效果不一样。

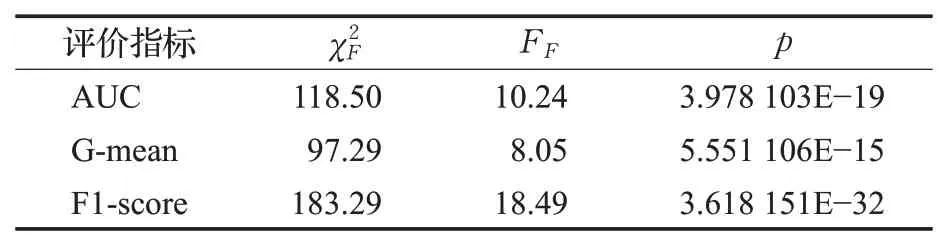
表3 14种算法在43个数据集上的Friedman检验统计值Table 3 Friedman test statistics of 14 algorithms on 43 data sets

同时利用Friedman检验得到了不同算法在43个数据集上三个指标的平均优劣排名次序，见图7～9。其中，算法的性能越好，排名就越靠前。在图7～9中离圆的中心点越近表明算法表现就越好，反之，离圆的中心点越远或者离圆的边界越近算法性能就越差。从图7～9中可以看出本文提出的方法在AUC和G-mean上明显优于其他算法。具体来说，在AUC上表现最好的三个算法为BPUS、EasyEnsemble和IHT，其平均排名次序分别为4.3、5.38、5.78，较差的为平均排名为10.6、10.2、9.23的NM、RBU和CNN算法。同理，在G-mean上可以得出相似的结论，性能最好的三个算法仍然为BPUS、EasyEnsemble和IHT，较差的为NM、AdaCost、CNN算法。在F1-score上表现较优的为SMOTE+Tomek、SMOTE-IPF、ENN和TomekLinks，IHT、AdaCost和BPUS表现居中，RBU、CC和NM表现最差。

图7 14种算法的AUC平均排名次序Fig.7 Average AUC ranking of 14 algorithms

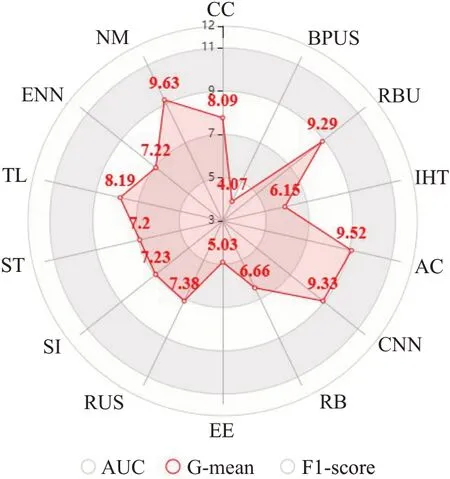
图8 14种算法的G-mean平均排名次序Fig.8 Average G-mean ranking of 14 algorithms

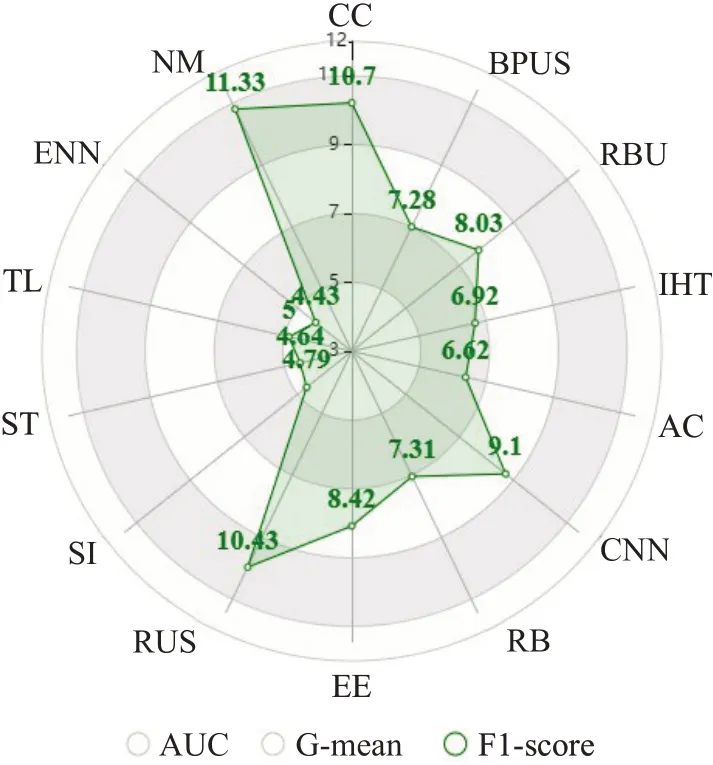
图9 14种算法的F1-score平均排名次序Fig.9 Average F1-score ranking of 14 algorithms

综上所述，本文提出的方法在43个KEEL不平衡数据上总体分类效果较好，尤其是在指标AUC和G-mean表现优异，这说明BPDDUS算法能够有效地加强分类器对关键多数类样本的重视，减少了重要信息的丢失。同时也证实了在进行欠采样时考虑样本的空间分布及局部信息的必要性和重要性。

4 结语

本文提出了一种基于贝叶斯后验概率的多数类集成欠采样方法，该方法利用贝叶斯后验K近邻估计充分挖掘多数类样本的局部信息，根据样本的空间分布尽可能准确地选取能够映射分类信息的重要样本，以提高后续模型训练的质量。通过与13种算法在43个数据集上的对比实验结果表明，BPDDUS是一种有效的不平衡数据预处理方法。另外，Friedman检验也证明了BPDDUS与13种经典采样方法存在显著性的差异，尤其在AUC和G-mean指标上，本文方法明显优于其他方法。

尽管如此，BPDDUS也存在一定的局限性。当数据集中少数类样本较少时，有限的少数类样本能够提供的信息十分有限，此时仅靠增加集成训练次数无法有效地提升性能。因此，如何在此类少数类样本极少的情况下，提升不平衡数据的学习性能值得进一步的研究。