三类笛卡儿积图的完美匹配计数

许丽丽

（闽南师范大学数学与统计学院,福建漳州 363000）

设G=(V(G),E(G))，其中V(G)表示G的顶点集，E(G)表示G的边集.子集M⊆E(G)，若M中任意两条边在图G均不相邻，则称M是图G的一个匹配.与M中的边相关联的点称为被M饱和的点.若图G的一个匹配饱和了图G的所有顶点，则称这个匹配为完美匹配.设C是图G的偶圈，若图G去掉该圈C上的点以及与这些点相关联的边后仍存在完美匹配，则称C是图G的好圈.设表示图G的一个定向，沿着一个方向在圈上走，定向与所走的方向相同的边的数目为奇数（偶数），则称这个圈在是奇定向（偶定向）的.若G中每一个好圈在都是奇定向的，则称这个定向为Pfaffian定向，具有Pfaffian定向的图为Pfaffian图.

图的完美匹配计数问题是图论的一个重要研究课题.基于化学家对芳香碳氢化合物的研究，图的完美匹配的计数问题从20世纪中叶开始受到了化学家的高度关注，他们发现化合物对应的共轭分子图是否具有完美匹配与该化合物的稳定性有一定的关系[1].所以研究图的完美匹配数具有重要的理论和应用的意义.

Valiant[2]证明了一般图中的完美匹配计数问题是NP—完全的.Kasteleyn[3]首次提出利用Pfaffian定向的方法去计算图的完美匹配数.若G中每一个好圈在都是奇定向的，则称这个定向为Pfaffian 定向，具有Pfaffian定向的图为Pfaffian图.

Kasteleyn[3]证明了所有平面图都具有Pfaffian 定向.而对于非平面图是否具有Pfaffian 定向这个问题还是一个公开问题.晏卫根等[4-5]证明了卡氏乘积图C4×T,P4×T以及P3×T（Ci表示顶点数为i的圈，Pi表示i-1长的路，T表示存在完美匹配的树）具有Pfaffian定向，并得到了其完美匹配计数公式.林峰根等[6]进一步证明了C4×G（G表示单圈非二部图）具有Pfaffian 定向，从而计算得到了它的完美匹配数的表达式.卢福良等[7]根据图G的禁止子图刻画了任意图G的卡式乘积图G×P2n和G×C2n的Pfaffian性质.本文证明了三类乘积图具有Pfaffian定向，并利用其斜邻接矩阵行列式得到了它们的完美匹配数的显示表达式.

1 乘积图的Pfaffian定向

设图G的顶点集为(v1,v2,…,v2p)，表示G的一个定向.定义的斜邻接矩阵为，1≤i,j≤n，其中

容易看出，当PM对应的划分不是图的一个完美匹配时，Pf(A)=0；Pf(A)的非零项对应图G的完美匹配.PM的符号定义为wPM的符号.如果中所有完美匹配的符号都相同，则这时称为Pfaffian 定向，具有该定向的图称为Pfaffian图.目前仍没有好的算法去判断一个图是否有Pfaffian定向.

一般地，一个图是否具有Pfaffian定向，以下几个条件等价.

定理1[8]若图G的顶点个数为偶数，是它的一个定向，下面四个条件等价：

3)图G中每个好圈在图都是奇定向的；

4)对于图G中任意一个完美匹配交错圈在图都是奇定向的.

Muir[9]得到了斜对称邻接矩阵的Pfaffian与该矩阵的行列式的关系.

定理2[9]令Α=(aij)m×m为一个斜对称矩阵，则A的行列式det(A)=(Pf(A))2.

定理3[8]若G是一个Pfaffian 图，是G的一个Pfaffian 定向，则G的完美匹配数w(G)=|Pf(A)|=.

如果一个图是Pfaffian图，那么它的完美匹配数可以通过某一定向下的矩阵的行列式得到.也就是它的完美匹配计数就能在多项式时间内算出.

定理4[10]若G是连通的Pfaffian 图，T是G的生成树，e∈E(G)是T中两端点距离为偶数的边.那么T+e的任意定向都可以扩展为G的一个Pfaffian定向.

引理1K1,m×P2n具有Pfaffian定向.

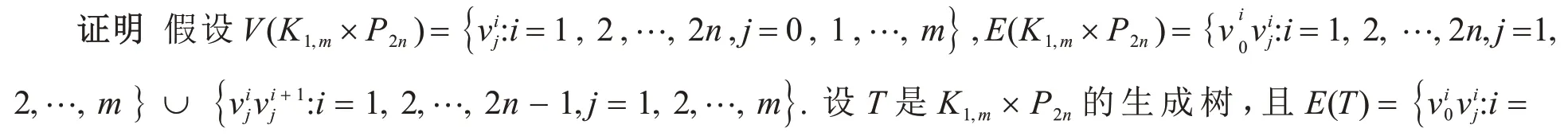
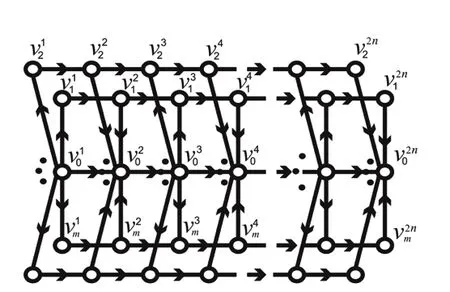
图1 K1,m×P2n的一个Pfaffian定向Fig.1 A Pfaffian orientation of K1,m×P2n

引理2K4×Pn具有Pfaffian定向.

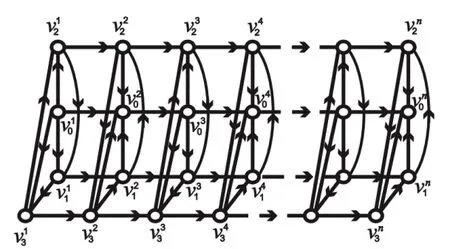
图2 K4×Pn的一个Pfaffian定向Fig.2 A Pfaffian orientation of K4×Pn

引理3若G是由有一条公共边的两个奇圈组成的图，则G×P4具有Pfaffian定向.

图3 G×P4的一个Pfaffian定向Fig.3 A Pfaffian orientation of G×P4

2 三类图的完美匹配数

在本节中，计算了K1,m×P2n,K4×Pn和G×P4（G是由有一条公共边的两个奇圈组成的）的完美匹配数.根据上节中所描述的Pfaffian 定向方法，给这些图的顶点采用适当的标号方式，得到它们的斜邻接矩阵如下所示：

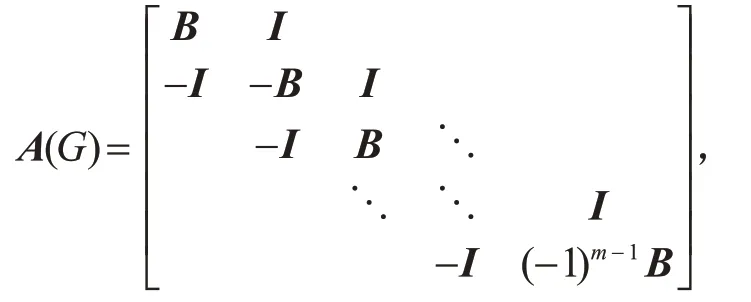
其中，

将矩阵A(G)进行初等变换，先将A(G)的分块矩阵的第一列乘-1，然后是第三行、第四行，接着是第四列、第五列，第七行、第八行分别乘-1，继续此操作，我们不改变行列式的绝对值，得到矩阵V,

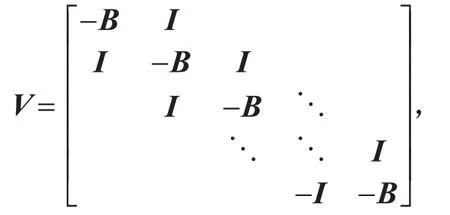
令

那么可以得到V=-I⊗B+C⊗I，其中⊗表示矩阵的克罗内克积，I表示单位矩阵.如果B的特征值为x1,x2,…,xm，C的特征值为y1,y2,…,yt.那么可以得到V的特征值为yj-xi,i=1,2,…,m;j=1,2,…,t.所以V的行列式为.

可以得到这几类乘积图的斜对称矩阵的特征值：

1)若G是K4×Pn，那么B的特征值为（它们的重数都是2）；

2)若G是K1,m-1×P2n，那么B的特征值为；

3)矩阵C的特征值为2cos((kπ)/(t+1)),(k=1,2,…,t)[11].

因此可以得到下面的结果.

定理5K4×Pn,K1,m×P2n的完美匹配数可以表示为

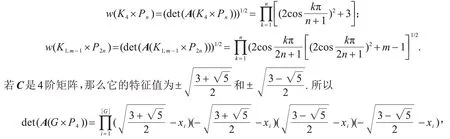
其中xi(i=1,…,s)是G的所有特征值.注意到，实斜对称矩阵的特征值要么为0，要么是虚数.如果x是实斜矩阵的特征值，则它的共轭也是实斜矩阵的特征值.因此我们有

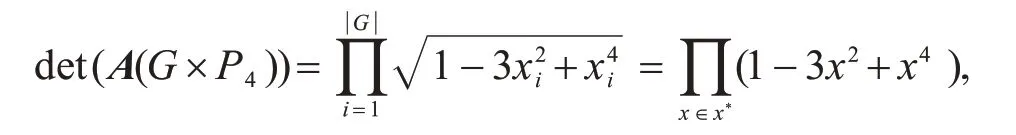
其中x*(G)是A(G)的所有特征值的非负虚部的集合.所以可以得到定理6.

定理6如果G由具有一条公共边的两个奇圈组成的图，那么w(G×P4)=,其中x的取值范围为A(G)的所有特征值的非负虚部.