零强迫数为最大度的树图
涂东鑫,陈鸿章
(闽南师范大学数学与统计学院,福建漳州 363000)
考虑的图为简单图.设图G为n阶简单图,其顶点集和边集分别为V(G),E(G).对任意v∈V(G),用dG(v)和N(v)分别表示顶点v的度和邻域;用δ(G)和Δ(G)分别表示图G的最小度和最大度.图G中度数为1的点称为悬挂点,用p(G)表示图G中悬挂点的数目.称v∈V(G)是图G的一个割点当且仅当ο(Gv)>ο(G),其中ο(G)表示G中连通分支的数目;称e∈E(G)是图G的一条割边当且仅当ο(Ge)>ο(G).用T和Pn分别表示树图和n个顶点的路图.对任意X⊆V(G),G[X]表示图G的一个由顶点集X导出的子图.其他未加定义的符号和术语,参考文献[1].
在介绍图的零强迫数之前,首先回顾一个染色规则:给图G的顶点集V(G)中染黑白两种颜色,设S⊆V(G)是G中所有染黑色的点集.对任意的点v∈S,v的所有邻点中仅有点u为白色,那么点v强迫点u染成黑色,这个染色过程称为强迫过程.从顶点集S开始,交替运用染色规则,最终使得G中所有点变为黑色,那么点集S称为G的一个零强迫集,而G的零强迫集中最小的顶点数目称为G的零强迫数,记为Z(G).
近年来,关于零强迫数的研究吸引了越来越多的学者关注,例如Amost 等[2]给出了图的零强迫数的上界:对具有n个顶点的简单连通图G,有Z(G)≤(n(Δ-2)+2)/Δ-1,其中Δ≥2.近期,Oboudi[3]研究了树图T的零强迫数与其最大度之间的关系,证明了Z(T)≥Δ(T)-1,并刻画了所有满足Z(T)=Δ(T)-1 的树图.受到上述文献的启发,本文进一步刻画了所有满足Z(T)=Δ(T)的树图.
1 预备知识
首先介绍几类树图.
类型1设T(n1,…,nk)是如图1 所示的树图,其中ni≥1,i=1,…,k且n=n1+…+nk-k+1,k是正整数.显然T(n1,…,nk)是一条路或者是星形树(只有一个顶点的度大于2的树).
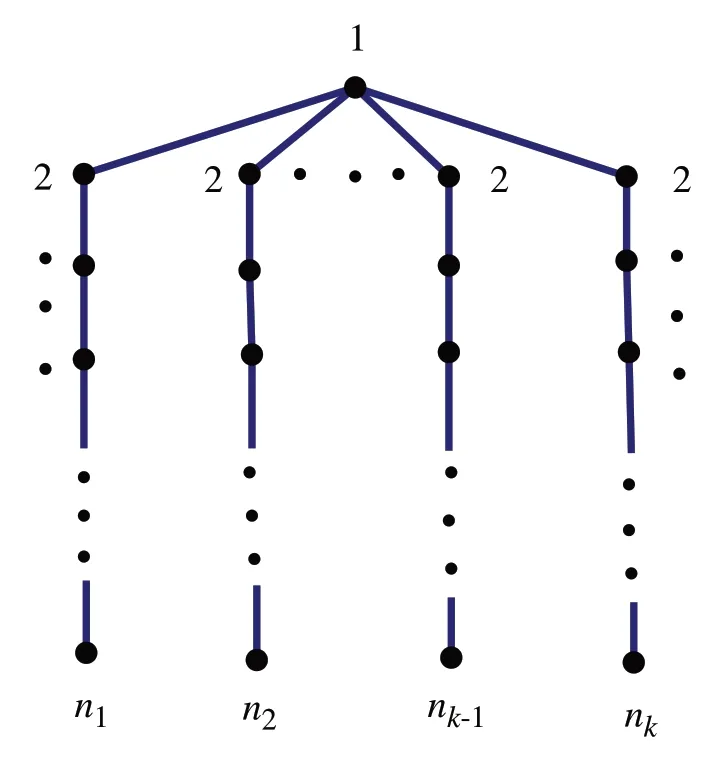
图1 类型1中的树图T(n1,…,nk)Fig.1 Tree graph T(n1,…,nk)in type one
类型2设T(m1,…,mk;n1,…,nk)是如图2 所示的树图,其中mi≥0,ni≥0,i=1,…,k且n=m1+…+mk+n1+…+nk+k+1,k是正整数.树T(1,2,0,1;2,1,0,0)如图3所示.
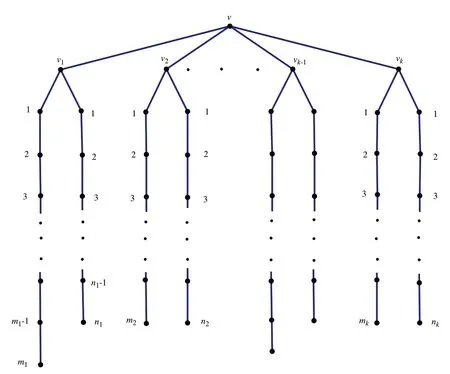
图2 类型2中的树图T(m1,…,mk;n1,…,nk)Fig.2 Tree graph T(m1,…,mk;n1,…,nk)in type two
图T(n1,…,nk)和图T(m1,…,mk;n1,…,nk)的最上层的顶点称为树图的根点.如图1的顶点1是它的根点,图2和图3的根点分别是v和u.
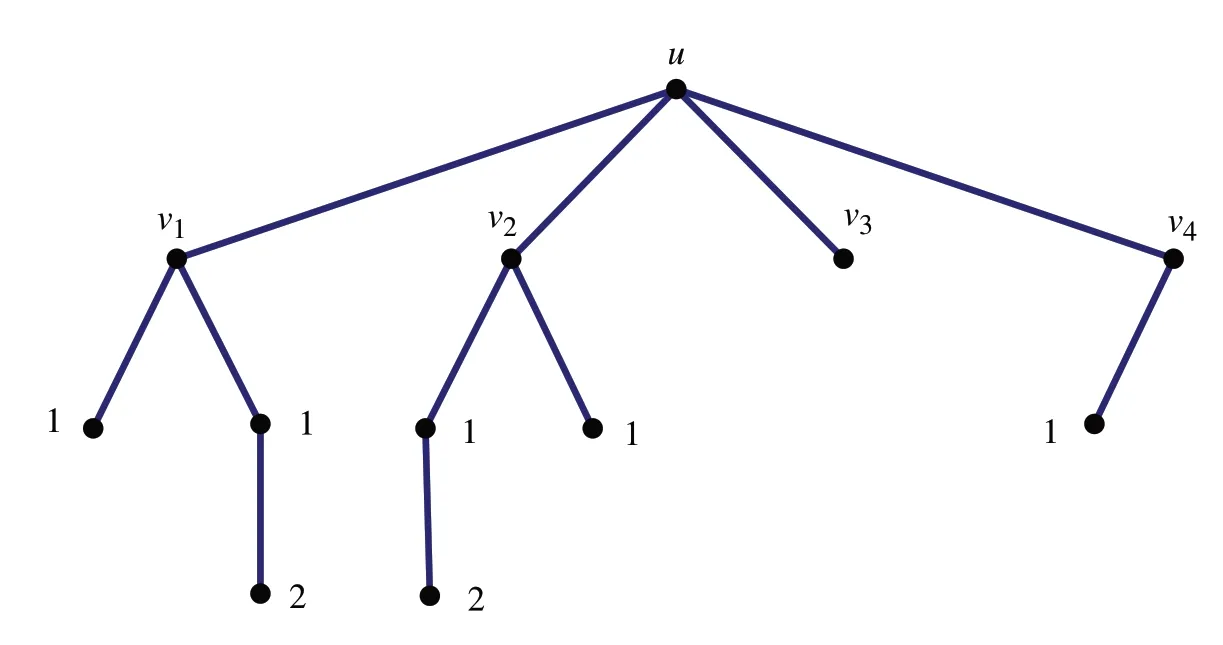
图3 类型2中的树图T(1,2,0,1;2,1,0,0)Fig.3 Tree graph T(1,2,0,1;2,1,0,0)in type two
注1当n1≥2,…,nk≥2 时,上述的两种图形可以进行转换,则有T(n1,…,nk)=T(n1-2,…,nk-2;0,…,0);其次T(n1,…,nk)和T(m1,…,mk;n1,…,nk)的根点只有一个.此外,零强迫集简称为强迫集,零强迫数简称为强迫数.
类型3对于以下四类树图T1,T2,T3,T4它们两个之间通过连接一条新边而得到三类新的树图ξ1,ξ2,ξ3,其如下所示:

1)ξ1表示通过一条边连接图T1的根点和图T2的任意悬挂点得到的图.
2)ξ2表示通过一条边连接图T1的根点和图T3的根点的任意度为2的邻点得到的图.
3)ξ3表示通过一条边连接图T4的根点和图T2的任意一点得到的图,且满足图T4的根点是图ξ3的最大度顶点.
其中ξ1和ξ2阶数为n=m1+…+mk-1+n1+…+nk-2+m1'+m2'+m3'+n1'+k+4,ξ3的阶数为n=m''1+…+m''k-1+n''1+…+n''k-3+m1'+m2'+m3'+n1'+k+4,且k=Δ(ξi)≥3,k是整数,i=1,2,3.
下面给出一些引理.
引理1[3]设T≠P1是一个具有n个顶点的树图,则Δ(T)-1≤Z(T)≤p(T)-1.
注2由引理1可得,当T不是Pn(n≥2)时,Δ(T)≥3,则Z(T)≥2.
引理2[3]设T是一个具有n≥3 个顶点的树图,则Z(T)=Δ(T)-1 当且仅当T=Pn或T=T(m1,…,mk;n1,…,nk-2,0,0),其 中k=Δ(T)≥3,n=m1+…+mk+n1+…+nk-2+k+1 和m1≥0,…,mk≥0,n1≥0,…,nk-2≥0.
引理3[3]设G是一个具有n个顶点的连通图,任意v∈V(G),v1,…,vt是G的悬挂点且N(v)={v1,…,vt},令S是G的任意一个零强迫集,则|S∩{v1,…,vt}|≥t-1.
引理4[4]设G是一个具有n≥2个顶点的连通图,对任意v∈V(G)或e∈E(G),有Z(Gv)-1≤Z(G)≤Z(Gv)+1或Z(Ge)-1≤Z(G)≤Z(Ge)+1.
引理5[4]设G为具有n个顶点的连通图,其割点为v.令V(Gv)=W1∪W2∪…∪Wk,其中,W1,…,Wk是Gv的各个连通分支的顶点的集合,Gi=G[Wi∪{v}]是由顶点集Wi∪{v}的导出子图,其中,1≤i≤k,则Z(G)≥+1.
引理6[5]设G是具有n个顶点的连通图,则Z(G)=1当且仅当图G是路Pn(n≥1).
引理7设G是一个通过一条边连接图H中的一个顶点v和图T(n1,…,nk)的根点得到的图,其中H是连通图,k=Δ(T(n1,…,nk))≥2和n1≥2,…,nk≥2,则Z(G)=Z(H)+k-1.
证明注意到点v是图G的一个割点,则Gv至少有2 个连通分支.由引理2 和引理5 可得Z(G)≥Z(H)+Z(T(n1,…,nk+1)-2+1=Z(H)+k-1.令ST是图T(n1,…,nk)的任意k-1 个悬挂点的集合,显然ST是图T(n1,…,nk)的一个强迫集.假设SH是图H的任意一个强迫集,容易验证ST∪SH是图G的一个强迫集,则有Z(G)≤k-1+Z(H)≤|ST∪SH|,因此Z(G)=Z(H)+k-1,证毕.
2 主要结论
文献[3]证明了树图T的零强迫数满足Z(T)≥Δ(T)-1,并刻画了满足Z(T)=Δ(T)-1的所有树图.下面进一步刻画满足Z(T)=Δ(T)的所有树图.
定理1设T为具有n≥2个顶点的树图,则Z(T)=Δ(T)当且仅当T为以下树图:
1)P2;
2)T(m1,…,mk;n1,…,nk-1,0),其中,m1≥1,…,mk-1≥1,n1≥1,…,nk-1≥1,mk≥0和k=Δ(T)≥3;
3)ξi,i=1,2,3.
证明充分性当T为上述中的三种图形,容易验证Z(T)=Δ(T).
必要性设T是任一树图,其最大度为Δ=Δ(T)且Z(T)=Δ(T),对Δ进行讨论.
当Δ=1时,此时n=2,显然,T=P2,由引理6,可得Z(P2)=1,满足Z(T)=Δ.
当Δ=2时,此时n≥3,显然,T=Pn,由引理6,可得Z(Pn)=1=Δ-1,不满足Z(T)=Δ.
当Δ≥3时,因为Z(T)=Δ,不妨令点v是T的最大度顶点,即d(v)=Δ,且v1,…,vΔ是点v的邻点.由于点v是T的割点,则Tv有Δ个分支,用T1,…,TΔ来表示.若T1,…,TΔ中有两个或两个以上不是路,由注2,引理4和引理6可得
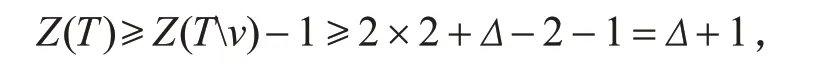
与假设Z(T)=Δ矛盾.所以只需要考虑以下两种情况:
情况1T1,…,TΔ都为路;
情况2T1,…,TΔ仅有一个不为路.
下面对这两种情况进行讨论.不失一般性,对T(m1,…,mΔ;n1,…,nΔ)类型的树图,假设mi≥ni≥0,i=1,…,Δ.
针对情况1,由于T1,…,TΔ是路,可知T=T(m1,…,mΔ;n1,…,nΔ).对于图形T(m1,…,mΔ;n1,…,nΔ)有以下三种情况.
情况1.1假设n1≥1,…,nΔ≥1,则m1≥1,…,mΔ≥1.下面对顶点数n进行数学归纳来证明Z(T)≥Δ+1.当顶点数n=3Δ+1 时,即当m1=…=mΔ=1 时,则n1=…=nΔ=1,vi邻接着2 个悬挂点,记为xi和yi,其中i=1,…,Δ.由引理3 可得,对于树图T的任意一个强迫集S,都有xi∈S或yi∈S,则|S|≥Δ.假设|S|=Δ,由于|S∩{xi,yi}|=1,则S⊆{x1,y1;…;xΔ,yΔ}.在染色过程中,vi被xi或yi强迫染为黑色,但最终每个vi都有2 个白色的邻点,得到矛盾,所以|S|≥Δ+1,即是Z(T(1,…,1;1,…,1))≥Δ+1.假设顶点数为n-1时,仍有Z(T)≥Δ+1结论成立.现在证顶点数为n的情况.假设max{m1,…,mΔ,n1,…,nΔ}≥2,不失一般性,假设m1≥2.设x是T1的悬挂点,使得dT(x,v1)=m1,且y是x的邻点,e=xy,则Te分别是图P1和图T(m1-1,m2,…,mΔ;n1,…,nΔ).运用归纳假设可得
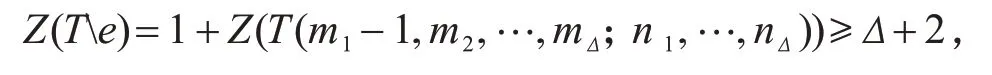
由引理4可得Z(T)≥Z(Te)-1 ≥Δ+1,与假设Z(T)=Δ矛盾.
情况1.2当ni=0,i∈{1,…,Δ},其余n1≥1,…,ni-1≥1,ni+1≥1,…,nΔ≥1.由引理1和引理2,可得Z(T)≠Δ-1 且Z(T)≥Δ-1,则Z(T)≥Δ,满足假设Z(T)=Δ.不失一般性,假设nΔ=0,其余n1≥1,…,nΔ-1≥1,则m1≥1,…,mΔ-1≥1,mΔ≥0.在图T(m1,…,mΔ;n1,…,nΔ-1,0)中取点集如下:当mi=0 时,取wi=vi;当mi≠0,取wi=ui,其中ui是Ti的悬挂点,满足dT(ui,vi)=mi,其中i∈{1,…,Δ}.令点集S={w1,…,wΔ},容易验证S是图T(m1,…,mΔ;n1,…,nΔ-1,0) 的一个强迫集,则Z(T)≤|S|=Δ,从而Z(T)=Δ,那 么树图T=T(m1,…,mΔ;n1,…,nΔ-1,0).
情况1.3当ni=nj=0(i≠j),i,j∈{1,…,Δ},其余为非负整数.由引理2 可得,Z(T)=Δ-1,与假设Z(T)=Δ矛盾.
针对情况2,不失一般性,假设TΔ不是路,显然Z(TΔ)=2.否则,Z(TΔ)≥3,根据引理4和引理6可得
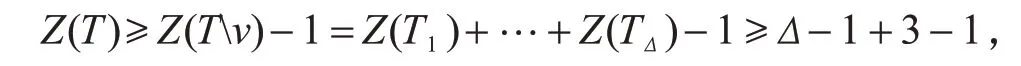
即Z(T)≥Δ+1,与假设Z(T)=Δ矛盾.进一步由引理2 可知Z(TΔ)=2 当且仅当TΔ=,其中.
记I1=,当=0;记I2=,当≥1.在树图T中,最大度顶点v与TΔ邻接的点为vΔ,不妨令v与vΔ邻接的边为e.由于Δ≥3,T1,…,TΔ-1分支是路,那么v与T1,…,TΔ-1邻接得到的图记为T(m1,…,mΔ-1;n1,…,nΔ-1),下面对图T(m1,…,mΔ-1;n1,…,nΔ-1)进行讨论,与情况1证明类似,同理对于图T(m1,…,mΔ-1;n1,…,nΔ-1)分以下三种情况.
情况2.1当n1≥1,…,nΔ-1≥1时,那么m1≥1,…,mΔ-1≥1,根据情况1.1可得
Z(T(m1,…,mΔ-1;n1,…,nΔ-1))≥Δ.在整个树图T中,根据引理4可得
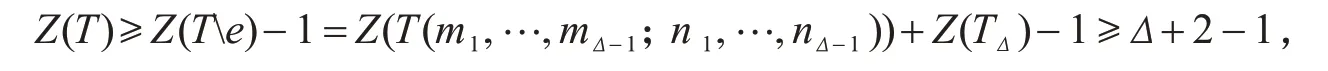
即Z(T)≥Δ+1,与假设Z(T)=Δ矛盾.
情况2.2当仅存在一个i∈{1,…,Δ-1}使得ni=0.不失一般性,假设nΔ-1=0,其余的n1≥1,…,nΔ-2≥1,那么m1≥1,…,mΔ-2≥1,mΔ-1≥0,这个图记为
T1=T(m1,…,mΔ-1;n1,…,nΔ-2,0),由引理1,引理2可得Z(T1)≥Δ-1.在整个树图T中,根据引理4可得
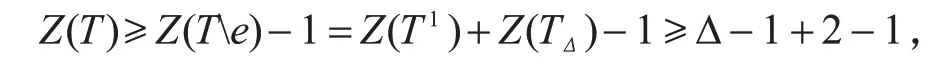
即Z(T)≥Δ,满足假设Z(T)=Δ.此情况下的树图T是通过一条边连接T1的根点v和TΔ的点vΔ得到的图形,接下来对TΔ中的点vΔ讨论如下.
当d(vΔ)=3 时,注意,此时的Δ≥4,否则与根点v是最大度顶点矛盾.由TΔ=I1或TΔ=I2,TvΔ得到T1和3个路Pn(n≥1).根据引理4和引理6可得
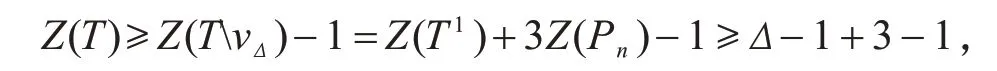
即Z(T)≥Δ+1,与假设Z(T)=Δ矛盾.
当d(vΔ)=2时,且TΔ=I1,此时Δ≥3,考虑以下两种情况.
1)当vΔ是TΔ的根点的邻点时,此时树图T等同于通过一条边连接图T(N1,N2)(N1,N2是不小于2 的整数)的根点与图T(m1,…,mΔ,n1,…,nΔ-2,0,0)的点vΔ得到的图.根据引理2和引理7可得
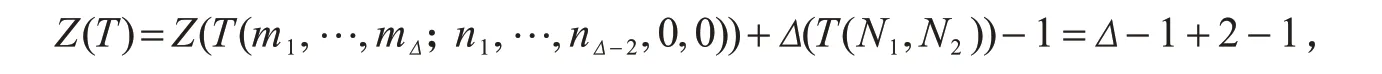
即Z(T)=Δ,此时树图T=ξ2.
2)当vΔ不是TΔ的根点的邻点时,TvΔ有3个分支,分别记为Q1,Q2,Q3,其中Q1∈T1,Q2∈I1,Q3∈Pn(n≥1).根据引理4和引理6可得
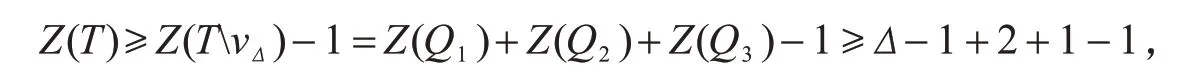
即Z(T)≥Δ+1,与假设Z(T)=Δ矛盾.
当d(vΔ)=2 时,且TΔ=I2时,TvΔ都有3 个分支,分别记为Q1',Q2',Q3',其中Q1'∈T1,Q2'∈{I1,I2},Q3'∈Pn(n≥1).根据引理4和引理6可得
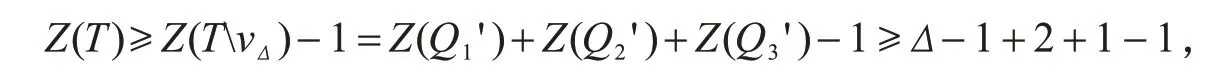
即Z(T)≥Δ+1,与假设的Z(T)=Δ矛盾.
当d(vΔ)=1,TΔ=I1或TΔ=I2,此时Δ≥3.对于图T1,与情况1.2 类似,同理找到T1的一个强迫集,记为S1={s1,…,sΔ-1}.在整个树图T中,根据染色规则,根点v会被T1的某个顶点强迫为黑色,且v只有一个白色邻点vΔ,那么v继续强迫vΔ染为黑色.由于Z(TΔ)=2,那么在TΔ中存在另外一个悬挂点,记为u1,使得点集{vΔ,u1}可以将TΔ所有点染为黑色.容易验证S1∪u1是T的一个强迫集,则Z(T)≤|S1∪u1|=Δ.由引理1,引理2可得Z(T)≥Δ,因此Z(T)=Δ.此时的树图T=ξ1.
情况2.3当ni=nj=0(i≠j),i,j∈{1,…,Δ-1},其余为非负整数.不失一般性,我们假设nΔ-1=nΔ-2=0,其余的n1≥0,…,nΔ-3≥0,那么m1≥0,…,mΔ-1≥0,这个图记为T2=T(m1,…,mΔ-1;n1,…,nΔ-3,0,0),则Z(T2)=Δ-2.在整个树图T中,根据引理4和引理6可得

整理可得Z(T)≥Δ,满足假设Z(T)=Δ.此情况下,树图T是通过一条边连接图T2的根点v和图TΔ的点vΔ得到的图形.在根点v是树图T的最大度顶点条件下,vΔ是TΔ上任意一点.在图T2取点集如下:如果mi=0,令wi1=vi,如果mi≠0,则令wi1=ui,其中ui是Ti的悬挂点,使得dT(ui,vi)=mi,i∈{1,…,Δ-2}.令点集S2=,容易验证S2是T2的一个强迫集.对于TΔ∈T(m1',m2',m3';n1',0,0),同理找到TΔ的一个强迫集,令其为点集S3={p1,p2},其中p1,p2∈V(TΔ).容易验证,S2∪S3是树图T的一个强迫集,从而Z(T)≤|S2∪S3|=Δ,即Z(T)=Δ,此时树图T=ξ3.证毕.

