碳交易市场均衡优化研究——基于演化博弈视角

张左敏暘，凌 静，冯 鲍

1.广西大学 经济学院，广西 南宁 530004；2.广西财经学院 研究生院，广西 南宁 530003；3.中国农业发展银行，广西 南宁 530028

随着全球气候变化形势日益严峻，碳达峰和碳中和已经成为全球共识，国际社会都在为早日实现这一目标而努力。习近平在第75 届联合国大会一般性辩论上提出：“二氧化碳排放力争于2030 年前达到峰值，努力争取2060 年前实现碳中和”。这一目标是我国立足新发展阶段、贯彻新发展理念，并充分考量和权衡了国际形势、国内现状及潜在成本等因素做出的重大战略决策，具有重要意义：一方面碳达峰、碳中和的实现能够优化我国能源结构，推动生态文明建设和经济的可持续发展；另一方面碳达峰、碳中和的实现能够减轻能源依赖，维护国家安全，也能防止我国陷入碳排放领域“单边主义”的困局。

有关抑制碳排放的措施和政策研究有不少积累，如刘雅芳[1]以福建生态文明先行示范区为例研究了生态文明建设对碳排放的影响路径，得到规模效应、结构效应、技术效应和生态保护效应是示范区建设抑制碳排放量的部分中介效应，但碳排放权的交易是从金融角度进行，与以往研究视角不同。碳交易是近年来全球应对气候变化的市场措施，试图通过市场经济机制实现绿色发展。实践证明依靠行政命令进行减排实现绿色发展有较大困难，通过市场机制引导，从企业利益层面出发能够更高效地实现绿色金融、绿色发展的目标。然而，正如Williamson[2]所说的交易成本，环境外部性给碳交易带来了交易成本，所涉及的成本包括了社会成本，因此会扭曲企业的决策行为，因此，交易制度会影响减排效果[3]。方国昌等[4]构建了政企博弈模型探索了这个问题。Dai等[5]使用一个可计算一般均衡模型回答了中国碳排放交易政策在不同部门之间的经济效应，计算发现，电力和航空部门的减排成本相对较高，往往是碳信用的主要购买者，而化工、非金属生产、钢铁、造纸等制造业部门的减排成本相对较低，往往是碳信用的主要卖家。碳排放交易中的激励机制、减排博弈以及合同选择问题正在被学者们研究，如赵新景[6]探析了“双碳”目标中碳交易的激励机制，石柳等[7]研究了林业纳入碳市场配额管理的综合减排效果，夏良杰等[8]研究了碳交易规制下过度自信制造商与减排服务商的减排博弈，王瑞等[9]研究了碳交易的能源枢纽主从博弈优化调度，郭雨等[10]研究了碳交易政策下节能服务公司参与减排的合同选择，王依婷等[11]研究了碳交易规制下供应链上下游企业绿色创新博弈。从经济学的均衡角度出发，Bosello 等[12]构建了一个多重地区可计算一般均衡模型讨论了在欧洲排放市场上“可避免的去森林化”能够降低减排政策的成本，并发现“可避免的去森林化”对于不同主体具有异质性，市场的结果并不能对每一个主体都合意。采用可计算一般均衡的还有Yu等人[13]，同样探讨在中国市场上碳配额的影响。在什么样的条件下碳交易市场才能达到帕累托最优均衡是本研究希望回答的问题。

理论上，现有相关文献探讨均衡时一般采用可计算一般均衡[14-16]，较少地构建博弈理论模型分析碳市场博弈的均衡结果；方法上，较少从三方演化博弈论的角度进行探讨。因此，企业在什么条件下愿意自己升级技术开发清洁能源产品，又是什么条件下愿意直接购买碳排放权？政府部门的监管动机又是什么？这些问题均涉及微观经济理论中的博弈，各方利益的博弈达到的均衡不同。因此，本研究的边际贡献在于较新颖地采用三方博弈理论，从经济学的成本出发，回答碳排放市场博弈均衡的性质并利用Matlab 进行仿真模拟，在此基础上给出相应的政策建议。

一、碳交易市场博弈模型的构建与分析

（一）理论分析

在碳排放中，为了使模型更具现实解释力，我们将企业类型分为两类，一类是普通工业企业，一类是公共生产企业，这样分类可以让我们更好地考察高碳排放和低碳排放部门的行为博弈。普通工业企业所需要排放的量是巨大的，根据《中国上市公司碳排放排行榜（2021）》，其中碳排放大户包括电力、水泥、煤炭、钢铁、有色金属等行业企业；相比之下，造纸、航运、综合、建材等非重工业制造大户所需要排放的碳较少，我们在模型中定义为公共生产企业。在存在碳交易市场的情况下，普通工业企业对碳排放的量需要权衡的是自己改进技术生产低碳产品的成本收益和购买碳排放权的成本收益，此时普通工业企业有两种策略选择，一种是选择改进技术生产低碳性产品，另一种是直接向他人购买碳排放交易权，两种情况下企业面临的成本和收益均是不同的。从《中国上市公司碳排放排行榜（2021）》看，碳排放大户均是各行业的龙头企业，因此对普通工业企业而言，其利润最大化要综合考量改进技术还是直接购买，这对其最终利润的影响较大，改进技术需要消耗当下的利润，普通工业企业是否愿意进行技术升级改造？而对于公共生产企业，本身的碳排放需求就小，其所需要考虑的问题为是否进行碳排放交易权的买卖，如果交易成本过高，其是否有动力进行交易？从政府部门出发，政府所面临的有碳排放达标的政绩考核要求，但是监管是有成本的，因此政府同样面临政绩考核和社会声誉和监管成本之间的权衡，有严格监管和宽松监管两种策略。

（二）模型基本假设

本研究考虑碳交易市场博弈模型，基于前文的理论分析，做出以下3 个基本假设：

假设1：碳交易市场博弈模型中存在三类博弈主体：普通工业企业A、公共生产企业B和政府机关C，博弈主体风险中性且均为有限理性。普通工业企业有“开发”“不开发”两种策略选择，公共生产企业则有“售卖”和“不售卖”两种策略选择，政府机关有“严格监管”和“宽松监管”两种策略选择。在本研究中，“开发”“售卖”和“严格监管”策略视为积极交易策略。

假设2：假定普通工业企业选择“开发”策略的比例为x(0 ≤x≤1)，选择“不开发”策略的比例为1-x；公共生产企业选择“售卖”策略的比例为y(0 ≤y≤1)，选择“不售卖”策略的比例为1-y，政府机关选择“严格监管”策略的比例为z(0 ≤z≤1)，选择“不严格监管”策略的比例为1-z。

假设3：“双碳”目标下，实现绿色低碳非常重要，假定政府宽松监管带来的公信力等损失高于政府因严格监管而付出的成本，即C3＜T。

根据上述假设，构建碳交易市场博弈模型的收益支付矩阵，如表1 所示。

表1 碳交易市场博弈收益支付矩阵

矩阵中参数的定义如下：

S1为普通工业企业不开发环保产品时的基本收益；S2为公共生产企业不售卖碳排放交易权的基本收益；S3为政府机关宽松监管时的基本收益；C1为普通工业企业开发环保产品所付出的成本；C2为公共生产企业售卖碳排放交易权的交易成本；C3为政府机关严格监管所付出的成本；H1为普通工业企业开发环保产品且公共生产部门售卖碳排放交易权时，普通工业企业得到的额外收益；H2为当开发环保产品且售卖碳排放交易权时，公共生产企业售卖所得到的新增收益；T为政府因不严格监管所带来的公信力损失以及其他的一些附加成本损失；P1为普通工业企业不开发环保产品所收到的惩罚；P2为公共生产企业不售卖碳排放权所收到的惩罚。

结合碳交易市场中的实际情况，提出假设4：假定交易市场中开发交易成本相对较高，普通工业企业碳产品的开发成本高于销售收益，公共生产企业碳排放交易权的交易成本高于售卖收益，即有C1＞H1、C2＞H2。而目前碳交易市场中存在的惩罚政策中惩罚值相对不高，会小于开发以及交易成本，即有C1＞P1、C2＞P2。

（三）博弈模型的构建

复制动态方程实际上是一种描述某一特定策略在一个群体中被采用的频数或频度的动态微分方程。

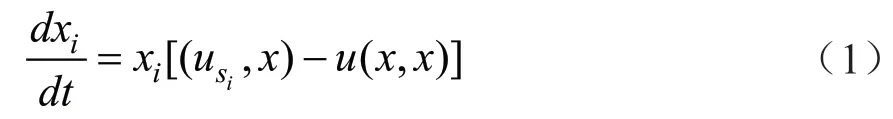
xi为一个种群采用纯策略si的比例或概率，表示采取纯策略时的期望，u(x,x)表示平均期望。在本研究中，假定普通工业企业选择“开发”策略时的期望值为Ex，平均期望值设为由此得到普通工业企业A选择“开发”策略的复制动态方程为：

同理，分别计算出公共生产企业B选择“售卖”策略和政府机关C选择“严格监管”策略的复制动态方程：

联立方程（1）、（2）、（3）得到碳交易市场博弈复制动态方程组，如（4）所示：

（四）模型的渐进稳定性分析

由式（4）可知，碳交易市场博弈系统I存在9 个局部均衡点，分别为E1（0,0,0）、E2（1,0,0）、E3（0,1,0）、E4（0,0,1）、E5（0,1,1）、E6（1,0,1）、E7（1,1,0）、E8（1,1,1）以及E9（x,y,z），其中（x,y,z）是方程组（5）的解。

由于E9不是严格的纳什均衡解，因此只考虑E1～E8。按照Friedman[17]提出的方法，通过分析系统的Jacobian 矩阵J可判定均衡点的局部稳定性。由式（5），可得系统I的雅克比矩阵：

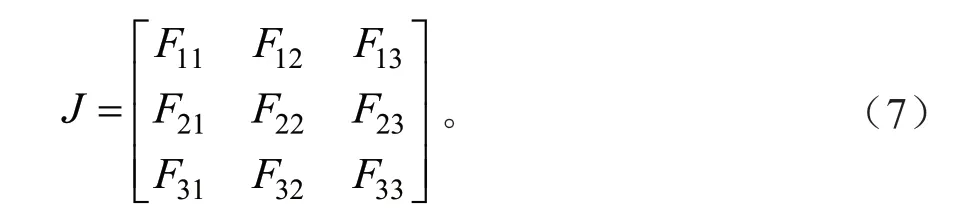
其中核心判断部分F11、F22、F33的值如下所示：

利用李雅普诺夫判定方法可以具体地对三维动力系统均衡点的局部稳定性进行判断[18]，由此得到系统I的8 个均衡点的局部稳定性分析，如表2 所示。

由表2 数据可知，E1（0,0,0）、E2（1,0,0）、E3（0,1,0）均为碳交易市场博弈系统I的鞍点，E4（0,0,1）为I的演化稳定策略（ESS）。对于局部均衡点E5（0,1,1）而言，当H1+P1＞C1时，其雅克比矩阵的正负性为（＋，＋,－），E5为鞍点；H1+P1＜C1时，其雅克比矩阵的正负性为（－，＋,－），E5亦为鞍点。对于局部均衡点E6（1,0,1），当H2+P2＞C2时，其雅克比矩阵的正负性为（＋，＋,－），E6为鞍点；H2+P2＜C2时，其雅克比矩阵的正负性为（＋,－，－），E6亦为鞍点。E7（1,1,0）为博弈系统I的不稳定点。E8（1,1,1）的雅克比矩阵正负性存在多种情形，当参数同时满足H1+P1＞C1、H2+P2＞C2时，其雅克比矩阵的正负性为（－，－，－），E8为博弈系统的ESS，这也是博弈系统的帕累托最优状态；当不满足上述条件时，E8为博弈系统的鞍点。综上所述，E4（0,0,1）恒为I的ESS，当满足H1+P1＞C1且H2+P2＞C2时，E8为博弈系统的ESS，E7为不稳定点，其余任何状态下，其余局部均衡点均为鞍点。

表2 碳交易市场下8 均衡点的局部稳定性判定

结合现实情况考虑，在“双碳”目标下，政府机关希望碳交易市场稳定，达到环保要求的同时提升经济发展，因此其会严格监管，但目前对于碳交易市场的管理仍在摸索，管理惩罚措施相对匮乏，惩罚力度不够，此种状态下对于普通工业企业和公共生产企业来说，其交易成本高于惩罚值，因此倾向于“不开发”策略和“不售卖”策略，即博弈系统最终收敛到E4（0,0,1）点，即（不开发，不售卖，严格监管）。当满足惩罚值和交易收益之和高于交易成本时，普通工业企业会选择开发环保产品，同时公共生产企业会选择售卖碳排放交易权，此时博弈系统又会多一个演化稳定策略，即（开发，售卖，严格监管）的帕累托最优状态。

二、因素影响演化结果的算例分析

在前文理论分析的基础上，本节运用Matlab对博弈系统中参与主体的行为演化进行数值模拟分析，并进一步分析各因素对博弈系统的具体影响机制。为便于分析，假定基本收益S1、S2、S3均为1；开发环保产品付出的成本C1为5，售卖碳排放交易权的交易成本C2为5，严格监管成本C3为2；普通工业企业交易收益H1为4，公共生产企业售卖收益H2为4；政府不严格监管带来损失T为3；不开发环保产品所受到的惩罚P1为3，不售卖碳排放权所受到的惩罚P2为3。上述初始条件同时满足H1+P1＞C1且H2+P2＞C2的参数条件，即按照前文分析，博弈系统此时有且仅有E4（0,0,1）和E8（1,1,1）两个演化稳定策略。考虑初始状态的随机性，除去研究初始策略比例时，其余研究中参与主体的初始策略比例均设为0.5。

（一）初始策略比例对博弈系统演化的影响

碳交易三方博弈系统的演化路径如图1 所示，X、Y、Z轴取值范围均为0 到1 之间，其中X轴表示普通工业企业选择“开发”策略的比例，Y轴表示公共生产企业选择“售卖”策略的比例，Z轴表示政府机关选择“严格监管”策略的比例。图1（a）采用5 点法进行模拟寻找演化方向，图1（b）是通过多点法模拟判定演化路径。

图1 博弈主体初始策略比例对系统演化路径的影响

可以发现，5 点法和多点法的演化方向和路径完全一致，均是在初始积极交易策略比例相对较低的情况下，博弈系统朝着（0,0,1）的方向演化，而在初始策略比例较高的情况下，博弈系统朝着（1,1,1）的帕累托最优状态进行演进。即在上述初始值的条件下，博弈系统I存在着（0,0,1）和（1,1,1）两个演化稳定策略，这验证了前文中的分析，证明了模型推导的准确性。同时博弈系统I演化的路径与主体的初始策略比例大小有关。各主体初始积极交易策略的策略比例越高，则I收敛到均衡稳定点（1,1,1）的概率越高，反之博弈系统收敛到均衡稳定点（0,0,1）的概率就越高，这表明在碳交易市场三方博弈系统中，各主体选择积极交易策略的比例越高，博弈系统就越朝着帕累托最优状态进行演化。

（二）交易成本C1、C2 对博弈系统演化的影响

在上述变量初始值保持不变的情况下，我们进一步数值仿真分析交易成本对碳交易市场博弈系统I的具体影响机制。为更贴合实际情况，假定主体初始策略比例为（0.5,0.5,0.5）。普通工业企业开发环保产品付出的成本C1对博弈系统I的影响如图2（a）所示，公共生产企业售卖碳排放交易权的交易成本C2对博弈系统I的影响如图2（b）所示。

图2 交易成本对博弈系统演化路径的影响

由图2（a）可知，当C1为2 或者4 时，博弈系统I收敛到（1,1,1），即博弈系统朝着（开发，售卖，严格监管）的方向演化，此时博弈系统朝着最优稳定状态进行演化；当C1增大到6 及6 以上时，博弈系统I开始收敛到（0,0,1），由此，存在一个临界值C1*，当满足C1＜C1*时，博弈系统I收敛到最优稳定状态（1,1,1），当满足C1＞C1*时，博弈系统I收敛到（0,0,1）。所以，为促使碳交易市场达到帕累托最优，要使开发环保产品付出的成本小于临界值C1*。

由图2（b）可知，当C2为2 或者4 时，博弈系统I收敛到（1,1,1），即博弈系统朝着（开发，售卖，严格监管）的方向演化，此时博弈系统朝着最优稳定状态进行演化；当C2增大到6 及6 以上时，博弈系统I开始收敛到（0,0,1），由此，同样存在一个临界值C2*，当满足C2＜C2*时，博弈系统I收敛到最优稳定状态（1,1,1），当满足C2＞C2*时，博弈系统I收敛到（0,0,1）。因此，为促使碳交易市场达到帕累托最优，要使售卖碳排放交易权的交易成本小于临界值C2*。

（三）交易收益H1、H2 对博弈系统演化的影响

同样，在上述变量初始值保持不变的情况下，我们进一步数值仿真分析交易收益对碳交易市场博弈系统I的具体影响机制。博弈主体的初始策略比例仍设为（0.5,0.5,0.5）。

图3（a）展示了普通工业企业交易收益H1的变化对博弈系统I演化的影响，由图可知，当H1为2 或者4 时，博弈系统I收敛到（0,0,1），即博弈系统将朝着（不开发，不售卖，严格监管）的方向不断演化，当H1增大到6 及8 以上时，博弈系统I开始收敛到（1,1,1），此时博弈系统朝着最优稳定状态进行演化，碳交易市场逐渐达到帕累托最优。由此，存在一个临界值H1*，当满足H1＞H1*时，博弈系统I收敛到最优稳定状态（1,1,1），当满足H1＜H1*时，博弈系统I收敛到（0,0,1）。所以，为促使碳交易市场达到帕累托最优，要使普通工业企业交易收益大于临界值H1*。图3（b）则展示了公共生产部门售卖收益H2的变化对博弈系统I演化的影响，由图可知，同样存在一个临界值H2*，当满足H2＞H2*时，博弈系统I会收敛到最优稳定状态，当满足H2＜H2

图3 交易收益对博弈系统演化路径的影响

*时，博弈系统I会收敛到（0,0,1）。同样地，为促使碳交易市场达向帕累托最优状态演化，要使公共生产企业售卖收益大于临界值H2*。

（四）惩罚值P1、P2 对博弈系统演化的影响

惩罚值对于博弈系统演化同样存在着重要的影响，在上述变量初始值保持不变的情况下，我们仿真分析惩罚值变化对碳交易市场博弈系统I的具体影响机制。博弈主体的初始策略比例仍设为（0.5,0.5,0.5）。

图4（a）展示了不开发环保产品所受到的惩罚P1的变化对博弈系统I演化的影响，由图可知，当P1为1 或者2 时，博弈系统I收敛到（0,0,1），即博弈系统朝着（不开发，不售卖，严格监管）的方向演化，当P1增大到5 及以上时，博弈系统I开始收敛到（1,1,1），此时博弈系统朝着最优稳定状态进行演化。由此，存在一个临界值P1*，当满足P1＞P1*时，博弈系统I收敛到（1,1,1），当满足P1＜P1*时，博弈系统I收敛到（0,0,1）。所以，为促使碳交易市场达到帕累托最优，要使不开发环保产品所受到的惩罚大于临界值P1*。图4（b）则展示了不售卖碳排放权所受到的惩罚P2的变化对博弈系统I演化的影响，由图可知，同样存在一个临界值P2*，当满足P2＞P2*时，博弈系统I会收敛到（1,1,1），当满足P2＜P2*时，博弈系统I会收敛到（0,0,1）。为促使碳交易市场达向帕累托最优状态演化，要使不售卖碳排放权所受到的惩罚大于临界值P2*。

图4 惩罚值对博弈系统演化路径的影响

三、结论与启示

（一）结论

由于碳排放存在较为严重的外生性问题，普通工业企业要权衡到底是自己开发生产低碳产品还是通过碳交易市场实现最终的碳排放目的，公共生产企业需要权衡是否进行碳排放交易权的买卖，政府也要权衡监管的成本。在此背景下本研究构建了一个普通工业企业、公共生产企业和政府机关的三方演化博弈模型，对模型进行求解并分析了各个均衡点的稳定性，进而通过Matlab 进行数值仿真，验证前文模型以及推导的准确性，并进一步探索交易成本、交易收益以及惩罚值等内部影响因素对博弈系统演化的影响，研究在什么样的条件下碳交易市场能够达成交易，并能够实现帕累托最优。得出以下具体结论：

第一，碳交易市场博弈系统I有8 个局部均衡点，其中E1（0,0,0）、E2（1,0,0）、E3（0,1,0）、E5（0,1,1）、E6（1,0,1）均为碳交易市场博弈系统I的鞍点，E（40,0,1）为I的演化稳定策略（ESS）。E7（1,1,0）为博弈系统I的不稳定点。E8（1,1,1）的雅克比矩阵正负性存在多种情形，当参数同时满足H1+P1＞C1、H2+P2＞C2时，E8为博弈系统的ESS，即当满足惩罚值和交易收益之和高于交易成本时，普通工业企业会选择开发环保产品，同时公共生产企业会选择售卖碳排放交易权，此时博弈系统会多一个演化稳定策略，即（开发，售卖，严格监管）的帕累托最优状态；当不满足上述条件时，E8为博弈系统的鞍点。

第二，数值仿真模拟下，在参数初始值满足既定假设条件的情况下，初始积极交易策略比例相对较低的情况下，博弈系统朝着（0,0,1）的方向演化，而在初始策略比例较高的情况下，博弈系统朝着（1,1,1）的帕累托最优状态进行演进。即在上述初始值的条件下，博弈系统I存在着（0,0,1）和（1,1,1）两个演化稳定策略，这验证了前文中的分析，同时也证明了模型推导的准确性。

第三，开发环保产品付出的成本C1、售卖碳排放交易权的交易成本C2、普通生产部门交易收益H1、公共生产部门售卖收益H2、不开发环保产品所受到的惩罚P1、不售卖碳排放权所受到的惩罚P2对博弈系统的演化均有着一定影响机制。存在一个临界值C1*，当满足C1＜C1*时，博弈系统I收敛到（1,1,1），当满足C1＞C1*时，博弈系统I收敛到（0,0,1）；存在一个临界值C2*，当满足C2＜C2*时，博弈系统I收敛到最优稳定状态（1,1,1），当满足C2＞C2*时，博弈系统I收敛到（0,0,1）。存在临界值H1*，当满足H1＞H1*时，博弈系统I收敛到（1,1,1），当满足H1＜H1*时，博弈系统I收敛到（0,0,1）；存在临界值H2*，当满足H2＞H2*时，博弈系统I会收敛到最优稳定状态，当满足H2＜H2*时，博弈系统I会收敛到（0,0,1）。存在临界值P1*，当满足P1＞P1*时，博弈系统I收敛到（1,1,1），当满足P1＜P1*时，博弈系统I收敛到（0,0,1）。存在临界值P2*，当满足P2＞P2*时，博弈系统I收敛到（1,1,1），当满足P2＜P2*时，博弈系统I会收敛到（0,0,1）。因此，为促进碳市场交易达到帕累托最优，要降低交易成本、提高交易收益、提高惩罚值。

（二）启示

从仿真结果中我们看出，影响帕累托最优均衡的内部因素主要包括交易成本、交易收益和惩罚值。因此，为更好地促进碳交易市场的稳定发展，根据上述研究结论提出以下几条政策建议：

第一，完善市场交易体制，降低交易成本。当前碳交易市场环境下，由于减排技术问题导致开发相关环保产品存在一定困难，客观上造成普通工业企业的开发成本偏高，而碳排放权交易市场制度不合理以及规则不完善则导致了公共生产企业售卖碳排放交易权的交易成本，几大因素综合作用导致交易成本较高，影响市场向帕累托最优状态演进。为降低交易成本，首先应该建立完善的市场交易体制，辅以配套的法律法规体系，尽快建立配额价格抑制储备和“柔性”市场调节机制，减少交易摩擦成本，提高社会福利；其次，应当大力鼓励创新环保技术，降低环保产品的开发成本，引导企业开发新能源产业、减少能耗与排放；最后，加快生态文明市场化机制的探索，鼓励各类金融机构参与碳排放权交易平台，提高碳交易市场流动性，降低交易成本。

第二，激发交易市场活力，提高交易收益。当交易收益较低时，严重影响碳市场向帕累托最优状态迈进。因此将政府主导的环境政策与碳交易市场相结合，坚持市场导向，尊重市场规律，出台相应法律法规规范市场，同时配套相应的激励机制与政策，激发交易市场活力，充分发挥市场作用，切实提高普通工业企业和公共生产企业的交易收益。同时创新碳金融市场，激发企业创新活力，推动碳交易市场朝拍帕累托最优状态迈进，逐步实现碳排放和碳中和目标。

第三，规范碳市场交易，提高惩罚值。中华全国工商业联合会提交的《关于进一步强化碳市场建设的提案》中明确指出目前碳交易市场的违约成本低，市场建设仍没有确立统一的发展观和现代化理念，市场法律支撑不足。因此，下一步的重点是规范碳市场交易，可以参考欧盟的碳排放交易市场规则，尽快出台配套政策以规范市场预期与行为，提高违约成本和惩罚。同时完善信息披露、市场监管与风险管理制度；建立健全碳排放权交易相关标准体系，如碳排放权交易会计处理规则、税务处理规则、碳排放权交易市场准入退出机制等。

总的来说，本研究的模型认为若要促进碳交易市场朝帕累托最优状态演化，要降低碳市场交易成本、提高碳市场交易收益，同时完善相关法律法规，惩罚值要相应地合理提高，从市场层面来看，只有所有参与主体均将社会发展视为自己的己任，都把节能减排纳入自己的决策当中并为之努力时，整体经济才能达到帕累托最优配置。进一步地从社会层面来看，给我们的启示是社会必须要将ESG 纳入综合考量并坚定不移地贯彻执行，必须要将社会成本与社会收益纳入企业的利润函数，以此企业能做出有利于社会的决策，为碳中和、碳达峰贡献自己的力量。