局部冲击下复合材料蜂窝夹芯结构的失效行为与吸能机理

薛 普，秦绪国，苏 伟，公 鑫，邓 健

（1. 北京航天长征飞行器研究所，北京，100076；2. 北京航空航天大学，北京，100191；3. 机械结构力学及控制国家重点实验室，南京，210016；4. 多功能轻量化材料与结构工信部重点实验室，南京，210016）

0 引 言

夹芯结构在保持轻质的基础上，充分利用不同组分的优势特性，提高结构力学性能，使整体结构具有更好的承载能力[1]。以蜂窝夹芯为代表的复合材料夹芯结构由于具有比强度高、比刚度高和抗冲击性能好等优势，在航空航天、交通运输、风力发电等领域得到广泛应用[2,3]。使用中，夹芯结构会面临诸多复杂受载情况，其中面外低速冲击引起的材料损伤与失效，给结构的承载能力带来巨大挑战[4]。因此，深入研究夹芯结构的失效机理和能量吸收规律十分必要。

一些学者[3,5～8]研究了不同的复合材料蜂窝夹芯结构的低速冲击响应，利用超声扫描显微镜对冲击后的结构进行无损检测，研究了夹芯结构的损伤形式和失效机理。此外，众多学者在试验研究的基础上开发了数值模拟研究方法，用以减少测试量和节约成本。

但是，目前对于复合材料夹芯结构低速多次冲击响应的研究尚不充分，本文采用数值仿真和试验两种方法分别研究了复合材料夹芯结构低速单次冲击和多次冲击的力学响应。数值模型考虑了面板的层间和层内损伤等不同失效模式，揭示了不同冲击能量下的吸能规律和损伤机制。多次冲击试验运用力-位移曲线对反复冲击载荷特性进行了讨论，也给出了不同冲击能量下蜂窝结构的力学行为响应。

1 材料本构模型

1.1 面板层内损伤模型

损伤模型包括损伤起始判据和损伤演化两部分。Hashin准则作为一种成熟的复合材料层合板损伤判据，后续还可结合损伤变量模拟损伤演化，被多款CAE软件采用，本文基于Hashin准则和渐进损伤演化建立面板的层内损伤模型。在连续损伤力学方法中，材料损伤表现为刚度矩阵的退化，模型定义了3个全局损伤变量，d1和d2是反映正交各向异性方向（即1方向和2方向）上纤维断裂状态的损伤变量，d12与基体微裂纹有关，反映剪切损伤状态。

损伤起始判据按损伤模式分为纤维损伤和基体剪切损伤。相应的起始破坏准则可以设定为

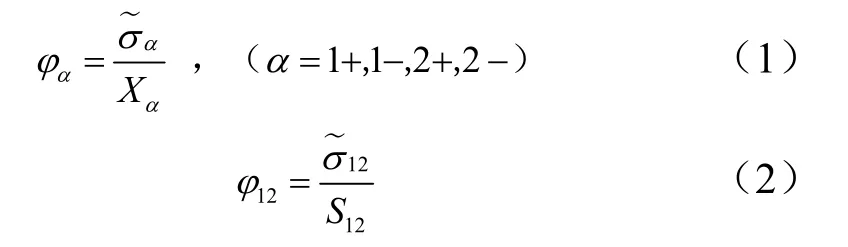
式中Xα为在每个纤维方向上单轴加载的拉伸或压缩强度；S12为剪切强度。当初始参数φα或φ12等于1时，将激活相应的损伤模式。是有效应力，定义为

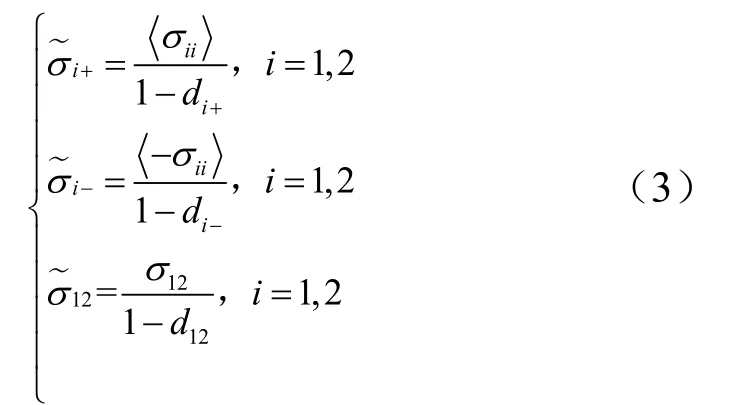
对于纤维损伤演化，采用指数柔化规律来模拟损伤变量的变化，损伤变量由0开始增加，直至变为1时，损伤演化过程结束。损伤变量的演化形式如下式：

式中gα0为损伤起始时的弹性能密度，即为元素的特征长度；Gfα为单轴拉伸或压缩载荷下每单位面积的断裂能；rα表示损伤阈值，初始值为1。

对于基体剪切损伤演化，根据文献[9]的假设，剪切损伤变量的变化规律如下：

式中α12＞ 0 ，≤1均为材料属性；r12表示剪切损伤阈值，初始值为1。

剪切损伤的模拟还与塑性有关，考虑塑性的损伤模型可以采用具有弹性域函数和硬化规律的塑性模型，用于描述受损材料中的有效应力，硬化规律的形式如下：

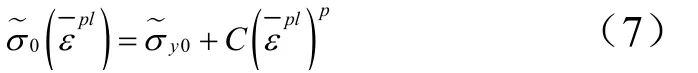
模型根据变形条件设置了基于损伤和基于变形的元素删除规则：当纤维方向的损伤变量或由于剪切变形引起的等效塑性应变达到预设值dmax或时，将激活基于损伤的元素删除准则；当拉伸或压缩对数主应变分别达到其最大或最小预设值时，将激活基于变形的元素删除准则。相关常数的取值根据文献[10]选取。

1.2 面板层间损伤模型

采用黏聚接触模型来模拟面板层间失效，在各铺层间设置黏聚接触属性。损伤起始判据采用二次接触应力准则，当接触应力比的平方和达到1时，损伤发生，判据可表示为如下形式：

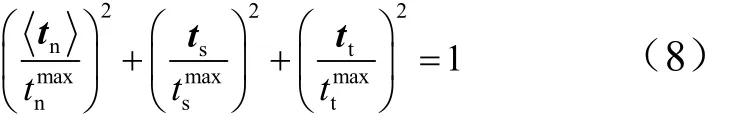
式中ti， (i=n,s,t)分别表示法向和两个剪切方向上的牵引应力矢量；timax，(i=n,s,t)分别表示法向强度极限和剪切方向强度极限。损伤演化采用线性软化规律，建立基于能量的损伤演化，使用混合模式，结合Benzeggagh-Kenane断裂准则，计算形式为

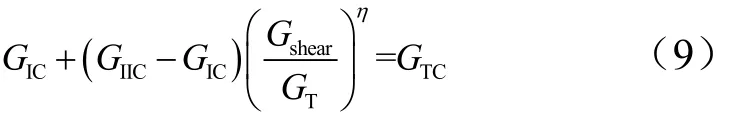
式中GIC，GIIC，GIIIC即3种开裂形式对应的断裂韧性，Gshear=GII+GIII，GT=GI+Gshear。根据文献[11]中的推荐取值，取η=1.45。

3 有限元模型

图1为复合材料蜂窝夹芯结构低速冲击有限元模型。模型包含4个部分：冲头、上下面板、蜂窝夹芯。冲头为半球形，直径12.5 mm，质量为8.95 kg，初始速度设为2.23 m/s。上下面板均为半径37.5 mm的圆形板，选用T300/CYCOM970织物材料，铺层顺序[（45/-45），（0/90），（90/0），（-45/45）]，单层名义厚度为0.22 mm，材料参数见表1。芯材为HexWeb HRH10-1/8-4蜂窝，尺寸为：L=4.2 mm，W=4.2 mm，T=7.2 mm；蜂窝单元简化考虑为单壁厚，设为t=0.07 mm。

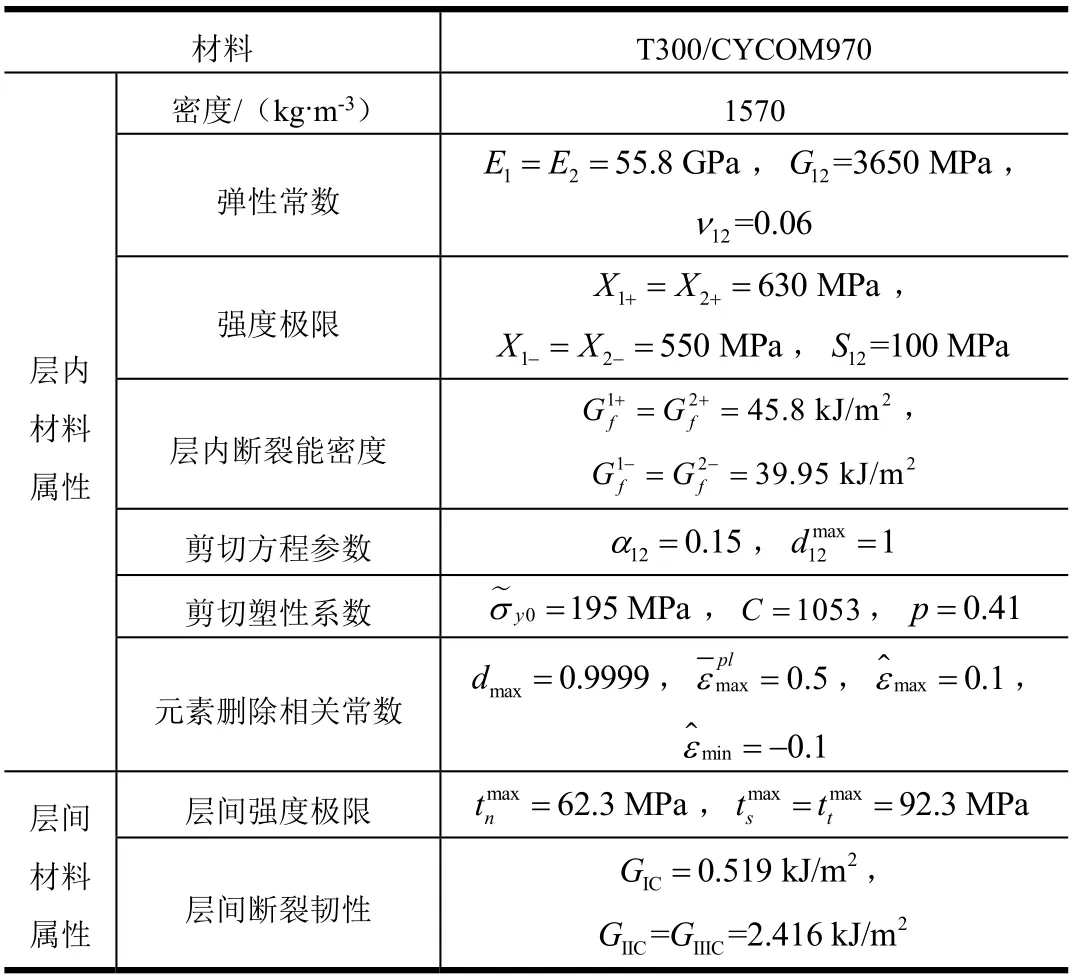
表1 T300/CYCOM970面板属性 Tab.1 Mechanical Properties of the T300/CYCOM970 Composites Facesheets

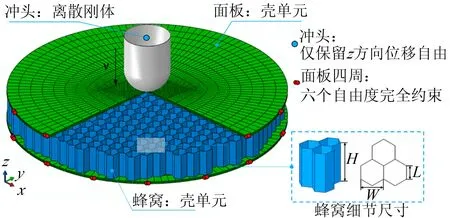
图1 复合材料蜂窝夹芯结构低速冲击有限元模型 Fig.1 Finite Element Model of Composite Honeycomb Sandwich Structures under The Low-velocity Impact，

基于ABAQUS/Explicit平台，建立复合材料蜂窝夹芯结低速冲击有限元模型。冲头建模为离散刚体，面板单层采用四节点减缩积分的壳单元（S4R）进行建模，再由四层堆叠得到完整模型。为了保证数值仿真结果的准确性，冲头下方区域的网格划分比其他区域更为密集。对蜂窝夹芯进行细节建模，考虑到蜂窝壁厚较小，采用S4R壳单元进行建模。蜂窝材料采用理想弹塑性模型，弹性模量设为E=1878 MPa，泊松比ν=0.3，塑性屈服应力为σy=27.21 MPa。

采用通用接触算法来计算和分析接触行为，定义的接触属性有：冲头与夹芯结构的接触、面板各单层间的接触、蜂窝夹芯与面板之间的接触以及蜂窝在压缩过程中发生的自接触。接触计算中，使用罚函数和“硬”接触的方式，设置摩擦系数为0.3，蜂窝单元间设为0.4[10]。与面板层间损伤的模拟相同，面板与蜂窝夹芯之间脱粘同样采用黏聚接触模型。损伤起始判据与损伤演化规律完全相同，接触属性的参数见表2。

表2 面板与蜂窝夹芯间接触属性 Tab.2 Interfacial Properties of The Facesheets and The Honeycomb Core

4 冲击仿真分析

4.1 冲击过程分析

图2记录了复合材料蜂窝夹芯结构在冲击过程中的损伤演变。如图2所示，其中：上面板冲击中心位置应力集中现象明显，损伤开始发生，面板与蜂窝夹芯接触、挤压，通过二者之间的界面传递压力和剪力，导致蜂窝夹芯产生了明显的压缩变形，即图中（a）时刻；上面板完全破坏时，冲击力达到第1个峰值，面板中心位移增大，蜂窝夹芯变形程度加大，即图中（b）时刻；随着冲头继续作用于夹层结构，蜂窝芯被逐渐压缩，但冲击力逐渐下降，主要原因是蜂窝夹芯的刚度比面板低，传递的载荷更小。直至冲头接触下面板，冲击力在大约0.004 s处达到谷值，即图中（c）时刻；由于下面板的高刚度和阻力，冲击力再次增加，下面板穿透，冲击力达到第2个峰值，即图中（d）时刻；到达（e）时刻，整个夹芯结构已经完全穿透，冲头在结构上留下一个孔，孔的周围区域应力集中现象明显，这些区域变形较大且摩擦剧烈。

图2 不同时刻夹芯结构的损坏程度及应力分布 Fig.2 Damage and Stress Distributions of Sandwich Structure at Different Time

为验证数值仿真的准确性，设定与文献[8]中试验相同的工况，并对比2种方法得到的峰值载荷和总吸收能量，结果对比如表3所示，可知误差均在可接受的范围内。

表3 仿真与试验结果比较 Tab.3 Comparison of Simulation and Experimental Results

冲击力-位移曲线的变化趋势与试验结果大体一致，但在峰值附近振荡剧烈，推测原因有以下2点：a）数值仿真分析步设定与真实试验相比冲击力数据的采集频率难以完全一致，试验过程中，由于冲击力传感器的不同，提取到的冲击力数据也会有差异，且传感器采集和传输数据会有一定的滞后性；b）数值仿真与试验得到的数据采用的滤波处理方式不同，因而试验曲线相对仿真曲线更为平滑。

4.2 冲击能量的影响

基于有限元模型，通过调整冲头的初始速度，分别研究了冲击能量为0.243 J、1.119 J、2.778 J、5.563 J、11.13 J、22.25 J时夹芯结构的响应，从而比较不同能量冲击下蜂窝夹芯结构的损伤力学行为。图3为不同冲击能量下冲头处于最大位移状态时夹芯结构的情况，颜色越深代表位移值越大。

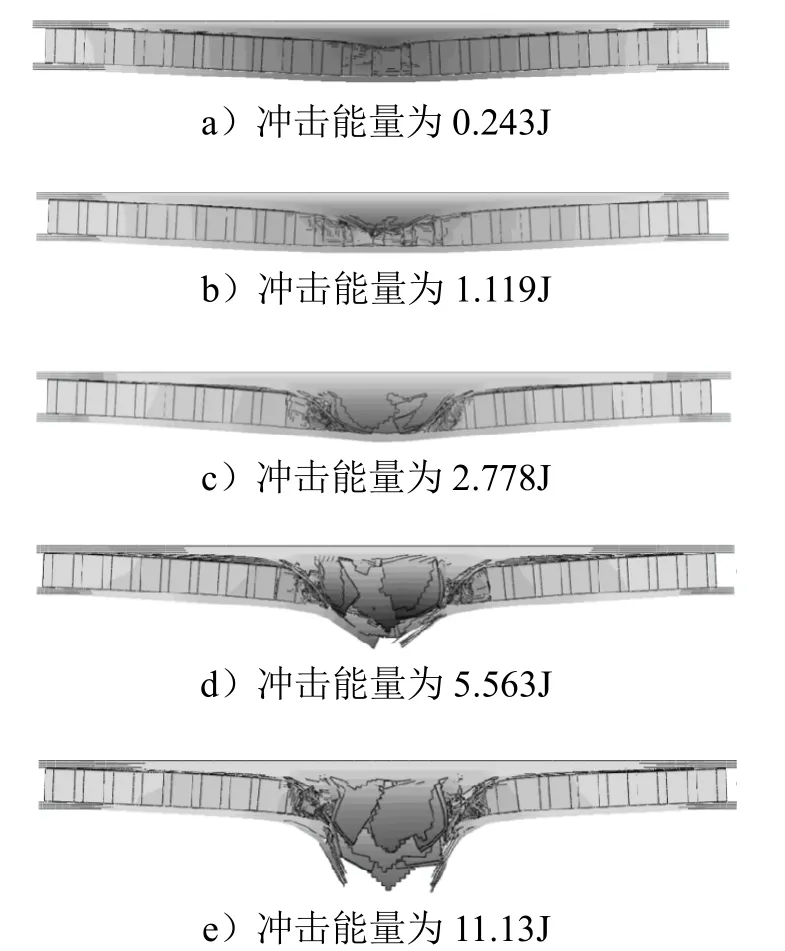
图3 不同冲击能量（速度）冲头位移最大时面板情况 Fig.3 Panel Conditions with Maximum Punch Displacement for Difference Impact Energies

由图3可知：

a）对于低冲击能量的夹层结构，前面板没有损坏，但出现分层，局部蜂窝压溃，损伤区域较小，如图3a所示；

b）随着冲击能量增加，冲头冲破上面板，开始压缩蜂窝，此时蜂窝呈现出逐级压缩的破坏形式，若能量较低，不足以完全压缩蜂窝，则会在能量耗尽后被弹回，如图3b所示；

c）若冲头能量足以将蜂窝完全压缩，则会接触下面板继续减速，在图3c的情况下，下面板最终没有损坏，冲头被弹回；

d）图3d中，冲头也没有穿透整个夹芯板，冲头的能量被夹芯结构完全吸收，在下面板的弹性恢复作用下回弹；

e）与22.5 J冲击能量非常相似，夹芯结构在 11.13 J冲击能量下被完全穿透，破坏面积达到最大，如图3e所示。

图4为不同冲击能量下的下面板中心位移对比。由图4可知，冲击能量越大，下面板中心处能够达到的最大位移越大。有所区别的是，不同的冲击能量冲击造成的下面板中心位移变化趋势不同。冲击能量极低时，下面板中心位移缓增，达到最大值后缓慢下降。冲击能量增大时，位移达到第一阶段最大值后会有一小段平台区，随后位移继续增加，直至最大值。若此时冲击能量耗尽，面板弹性变形恢复，中心位移逐渐减小；反之，若能量尚未完全耗尽，冲头继续向前，但由于下面板变形已经达到极限，中心位移基本保持不变。

图4 几种冲击能量的下面板中心位移曲线对比 Fig.4 Comparison of the Center Displacement Curve of the Lower Panel for Various Impact Energies

仿真结果表示，平台区出现在上面板最初发生破损时，由于面板开裂主要失效形式是纤维断裂，选取上面板四个铺层1方向和2方向拉伸损伤变量分布情况绘制云图，如图5所示，该工况冲击能量为22.25 J，对应0.001 s至0.002 s平台区内的4个时刻，涵盖了从裂纹形成及扩展的全过程。由此推测，出现平台区的原因是上面板的完全失效是一个渐进的过程，裂纹的扩展需要一定的时间，此时冲头与面板接触产生剧烈的摩擦和压缩，位移变化极小。

图5 22.5J冲击能量上面板各铺层拉伸失效损伤变量 Fig.5 Tensile Failure Damage Variables for Each Ply of The Upper Panel for 22.5J Impact Energy

5 多次冲击试验研究

5.1 试验准备

试验件为碳纤维面板和Nomex纸蜂窝粘接而成的蜂窝夹芯结构，如图6所示。蜂窝长宽高为：150 mm×100 mm×15 mm，纸蜂窝的壁厚为0.2 mm，边长为3.1 mm。碳纤维面板尺寸为：152 mm×102 mm×1 mm。本文采用INSTRON冲击试验机按照ASTM D7156标准进行冲击试验。配备数据采集系统记录冲击过程中的冲击力、位移数据，得到冲击力-位移曲线后可用于分析冲击过程中夹芯结构吸收的能量。

图6 低速冲击试验件 Fig.6 Test Specimen for Low-velocity Impacts

5.2 试验及结果分析

为确定结构的冲击性能，对夹芯结构进行单次冲击试验，设置5 J、10 J、15 J、20 J共4组冲击能量。其中，5 J、10 J和15 J冲击能量下结构均未完全破坏，可用于研究多次重复冲击，冲击力-位移曲线如图7所示。

图7 重复冲击试验冲击力-位移曲线 Fig 7 Force-displacement Curves of Repeated Impact Tests

首先研究了5 J冲击能量下的结构失效行为。夹芯结构承受22次冲击后完全破坏。由图7a可以看出存在4种冲击破坏状态。其中，状态1上面板吸能，但尚未破坏，芯材也没有出现明显损伤；状态2上面板已经破坏，但上面板结构在破损处存在堆积，芯材未产生明显破坏；状态3上面板和芯材均产生破坏，下面板未产生破坏；状态4是最主要的破坏模式，上下面板和芯材均出现破坏，但是由于下面板相对于上面板受到的弯矩较小，且冲击能量可向外传递至平台，因此下面板可承受多次冲击。

冲击能量增至10 J，结构由受到22次冲击破坏变为受到6次冲击破坏，从图7b中可以看出：上面板在第1次冲击下接近破坏，第2次冲击后上面板和芯材均完全破坏；通过进一步观测试验过程发现，第2次冲击后芯层的冲击路径上产生了较多失效碎片堆积，且结构在承受3次冲击后，芯层堆积碎片被挤压到冲击路径外，最后一次冲击引起了下面板的最终失效。由此可知，在低速重复冲击过程中，芯层的摩擦耗损起到了明显的吸能作用。

当冲击能量达到15 J时，循环冲击次数为3次，如图7c所示，第1次冲击导致上面板完全破坏并造成芯材的部分损坏；第2次冲击导致芯材完全损坏、下面板出现损伤；第3次冲击下面板完全破坏。

综合可知，冲击能量的增加显著降低了结构重复冲击次数。

6 结 论

本文针对复合材料蜂窝夹芯结构的低速冲击问题，建立了考虑失效模式的有限元模型，有效模拟了低速冲击下面板及蜂窝夹芯的损伤，基于有限元模型研究了冲击能量对低速冲击响应的影响，最后对多次冲击进行了试验研究。研究得到以下结论：

a）单次冲击下，低能量冲击工况与高能量冲击工况差异显著，冲击能量越高，夹芯结构的破坏情况越严重，下面板中心位移越大；

b）多次冲击直至破坏时，下面板承受了大部分次数的冲击，芯材的抗冲击能力较弱，在力-位移曲线中，芯材破坏的阶段较短；

c）随着冲击能量的增加，结构冲击响应变化明显，重复冲击的破坏次数大大降低。