弹箭螺纹连接松动机理分析研究

王 婕，卢红立，冯韶伟，王 帅，巩 浩

（1. 北京宇航系统工程研究所，北京，100076；2. 北京理工大学，北京，100081）

0 引 言

螺纹连接是航天型号中应用最广泛的连接形式之一[1～3]，其连接可靠性对发射任务成败有着重要影响。螺纹连接失效类型多，松动是其中最常见的失效模式之一[4,5]。随着航天事业不断发展，运载火箭、导弹武器、人造卫星等航天产品服役环境日趋复杂，工况条件愈加恶劣，螺纹连接系统经常或始终处于振动环境中，极易造成螺纹间发生相对运动，从而引起螺纹连接松动，最终导致螺纹连接失效，影响航天型号装配及发射流程，给航天产品可靠性带来严重影响[6～8]。

当前，中国在螺纹连接松动机理方面的研究尚不够深入、透彻，对防松措施的指导缺乏完善的理论依据，不同形式的外部振动载荷对螺纹松动的影响规律尚待研究与揭示。因此，本文通过有限元仿真分析方法，系统研究多种外部振动载荷单独作用以及耦合作用对螺纹连接松动的影响规律。

1 螺纹连接的有限元建模

早期对螺纹连接进行有限元建模时大多采用轴对称模型，这种模型忽略了螺旋升角，便于简化分析螺纹面的应力分布和应力集中，显然无法用于分析螺纹连接松动。后来，学者们建立了考虑螺旋升角的有限元模型，例如，四面体自由化网格模型，中间有圆柱孔的六面体网格模型，螺纹和螺杆单独建模并绑定的有限元模型。第1种模型采用四面体自由化网格，计算精度较低，第2种和第3种模型和实际的螺纹连接形状存在差异。直到2008年，Fukuoka和Nomura[9]提出了一种全新的、精确的螺纹建模方法，根据该方法构建的螺纹连接有限元模型全部采用六面体网格，稀疏过度合理，网格质量和计算精度较高，且和实际的螺纹连接形状非常吻合，本文将采用这种建模方法对螺纹连接进行有限元建模。

1.1 螺纹横截面轮廓的数学表达式

图1a是沿轴向剖面的一个螺距的外螺纹轮廓，r为外螺纹面到轴线的距离，在螺纹牙根部有一个半径是ρ的圆弧，因此，外螺纹面可以分为3个不同的部分：A-B（螺纹牙根部分）、B-C（螺纹侧面部分）和C-D（螺纹牙顶部分）。将这3部分扩展到平面，可以获得螺纹横截面轮廓，如图1b所示，事实上，任意横截面轮廓都是通过图1b所示的横截面轮廓旋转一定的角度获得的。选择螺纹牙根部作为起始点，θ为螺纹横截面轮廓上的点相对起始点的转角，r和θ的数学关系为

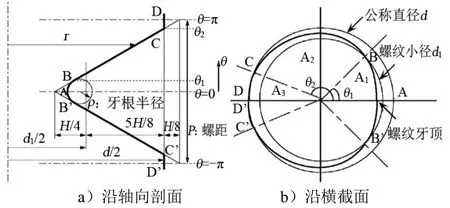
图1 外螺纹牙沿轴向剖面和横截面的轮廓 Fig.1 Profile of External Thread Along Axial Section and Cross Section

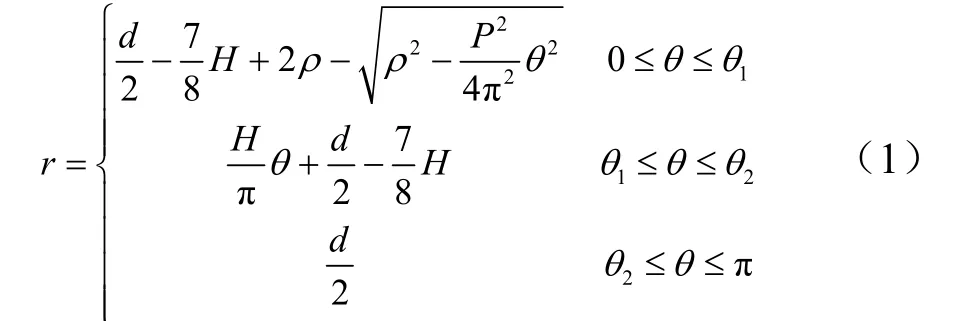
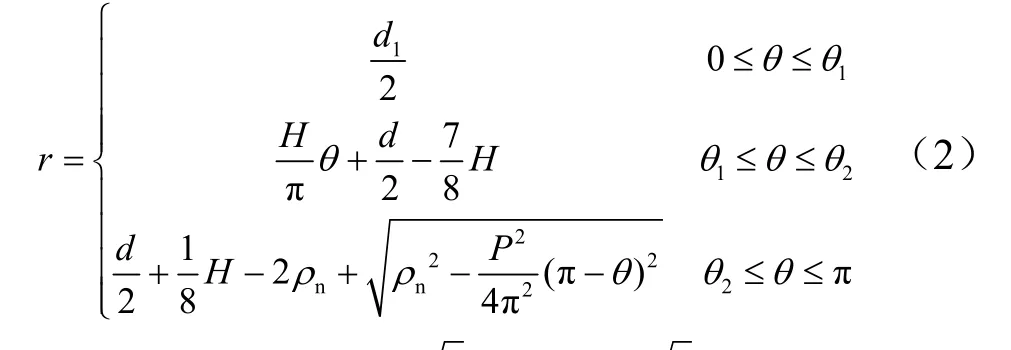
1.2 螺纹连接精确的网格划分

以外螺纹为例，通过以下6个步骤实现一个螺距的螺纹牙网格划分：a）对横截面的二维螺纹进行网格划分，得到一个基本的网格模型；b）将二维网格模型复制、旋转22.5°，向上平移P/16的距离，这两个二维网格模型将生成一个三维网格模型；c）将三维网格模型同样复制、旋转22.5°，向上平移P/16的距离，形成新的三维网格模型；d）将第3步得到的三维网格模型复制、旋转45°，向上平移P/8的距离，得到新的三维网格模型；e）将第4步得到的三维网格模型复制、旋转90°，向上平移P/4的距离，形成新的三维网格模型；f）将第5步得到的三维网格模型复制、旋转180°，向上平移P/2的距离，最终得到一个螺距的螺纹牙网格。

接着对一个螺距内的芯轴部分进行网格划分，该部分几何形状是一个圆柱，为了同时兼顾网格质量和计算效率，对内部区域采用粗网格划分，对外部区域则采用细网格划分。将上述一个螺距内的螺纹牙网格与芯轴网格合并，即可得到一个螺距内的完整网格。需要说明的是，通过合理的设计螺纹牙部分及芯轴部分的网格，可以使得二者在界面处的节点完全重合。通过复制与平移的操作可以得到整个外螺纹部分的网格，补充光杆及螺栓头部的网格，即可实现对整个螺栓的网格划分，如图2所示。按照类似的方法，可以实现对内螺纹的网格划分，如图3所示。图4为最终构建的螺纹连接有限元模型。

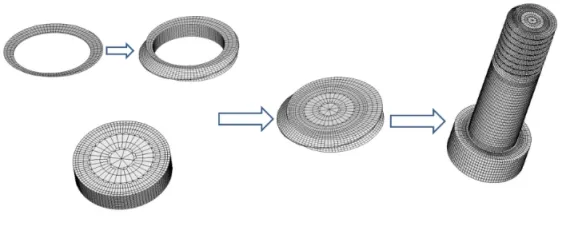
图2 螺栓的有限元网格划分 Fig.2 Finite Element Mesh Partition of Bolts

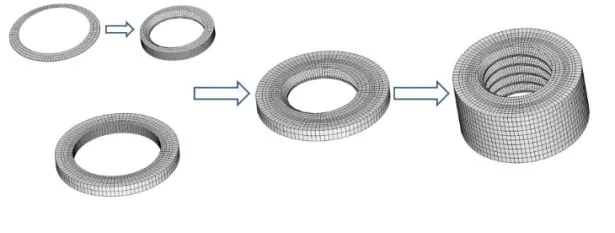
图3 螺母的有限元网格划分 Fig.3 Finite Element Mesh Partitin of Nut

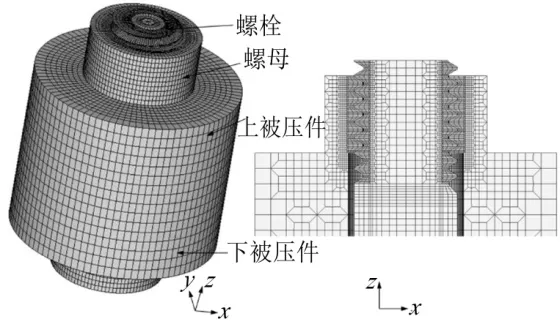
图4 螺纹连接的有限元模型 Fig.4 Finite Element Model of Screw Connection

2 外部振动载荷的有限元仿真

2.1 模型参数设置和边界条件

螺纹连接的公称直径是M10，螺距P=1.5 mm，有限元模型采用的实体单元类型是SOLID 185，材料的弹性模量和泊松比分别为206 GPa和0.3。有限元模型中有4对接触界面：螺纹接触界面、螺母和上被压件接触界面、上下被压件接触界面、下被压件和螺栓接触界面，接触界面包括接触面和目标面，接触面和目标面分别采用CONTA173单元和TARGE170单元进行网格划分，上下被压件的界面摩擦系数设置为0，其他界面的摩擦系数均设置为0.15，边界条件是下被压件底部全约束，见图5。

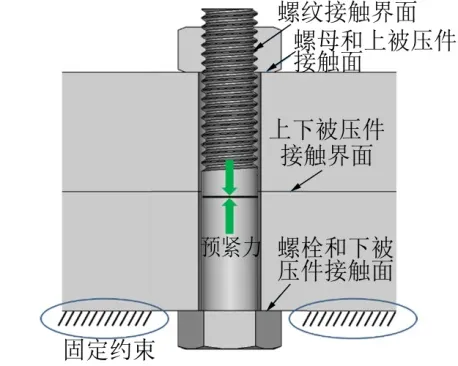
图5 有限元模型边界条件设置 Fig.5 Boundary Condition Setting of Finite Element Model

为了保证有限元结果的求解精度，还进行了网格无关性分析，最终确定有限元网格数量在160 000个左右，网格划分通过Hypermesh 12.0®实现，有限元求解过程均在ANSYS 16.0®中进行。

2.2 外部振动载荷仿真

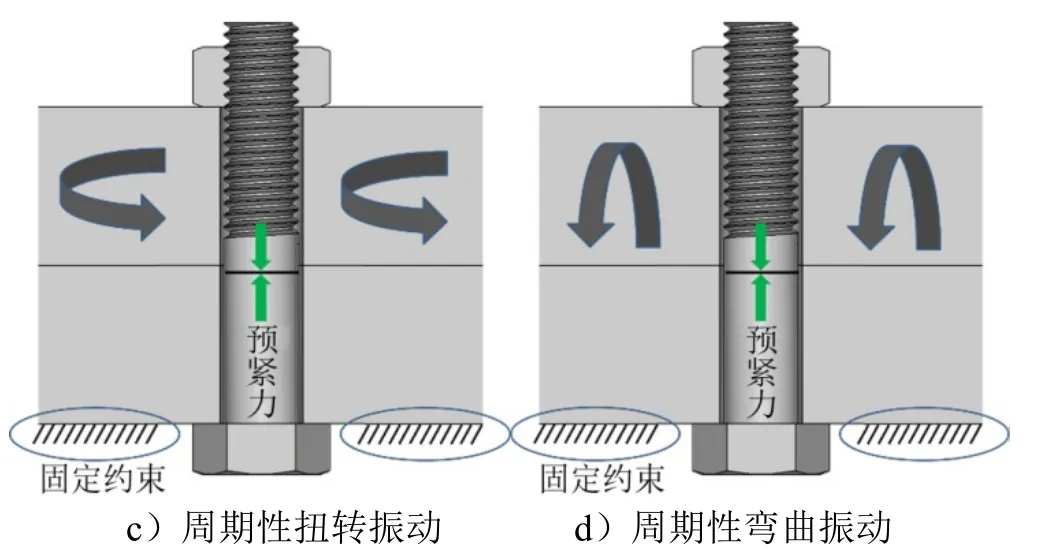
本节考虑的外部振动载荷包括轴向振动、横向振动、扭转振动和弯曲振动。外部振动载荷加载示意如图6所示。

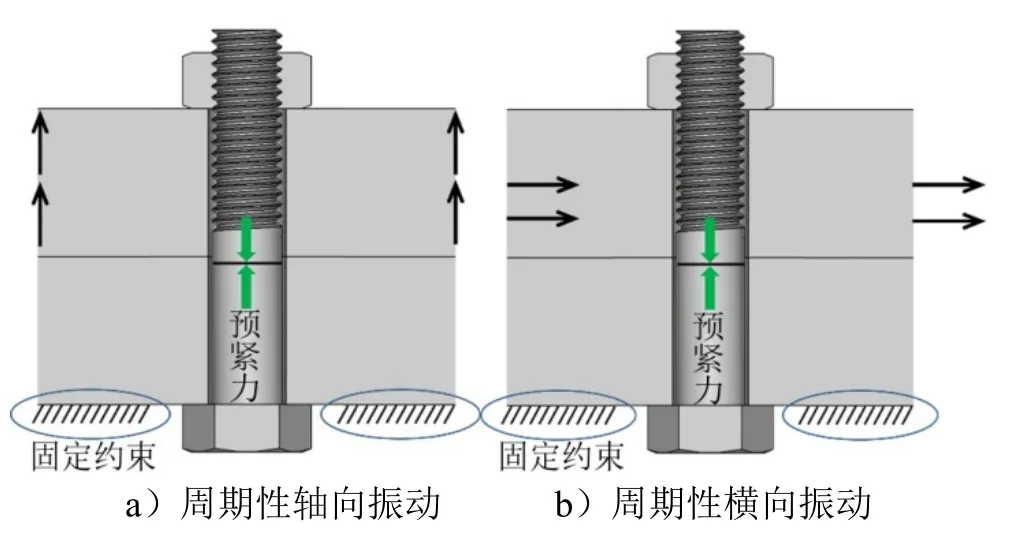
图6 外部振动载荷加载示意 Fig.6 Loading Diagram of External Vibration Load

续图6

轴向振动和横向振动直接对上被压件的圆环面节点施加，如图6a和图6b所示。扭转振动和弯曲振动的施加类似于螺母拧紧仿真，先选定一个自由节点，将自由节点和上被压件外圆环面通过MPC184单元进行耦合，对自由节点施加沿z方向和x方向的力矩即可产生扭矩和弯矩，如图6c和图6d所示，所有的加载过程均是准静态的，不考虑振动频率的影响。

3 外部振动载荷对螺纹连接松动的影响规律

3.1 外部振动载荷单独作用

对于横向振动，横向力大小分别设为450 N、750 N、1050 N和1350 N；对于轴向振动，轴向力大小分别设为2500 N、5000 N、7500 N和10 000 N；对于扭转振动，扭矩大小分别设为2500 N·mm、5000 N·mm、6000 N·mm和7500 N·mm；对于弯曲振动，弯矩大小分别设为25 000 N·mm、50 000 N·mm、75 000 N·mm和100 000 N·mm。施加上述4种不同形式的振动载荷，预紧力随振动周期的变化趋势如图7所示，从图7中可以看出，施加周期性轴向振动和弯曲振动时，螺纹预紧力随着振动周期增加而轻微增加，这主要因为预紧力是通过端面压强和面积的积分求得，在外力作用下，端面压强可能发生轻微变化，导致预紧力计算结果存在增大的可能，这也说明这两种振动载荷不会导致螺纹连接松动。对于横向振动，可以看出，在前几个振动周期，预紧力非线性变化，这主要因为螺纹发生了非旋转松动，随后，旋转松动导致螺纹预紧力持续衰退，且横向力越大，衰退速度越快。对于扭转振动，类似地，在前几个振动周期，非旋转松动导致预紧力快速下降，随后预紧力下降主要由旋转松动导致，经过计算，扭矩过大（7500 N·mm）或过小（2500 N·mm），旋转松动导致的预紧力衰退都比较小，当扭矩大小是5000～6000 N·mm时，预紧力衰退最明显。经计算，横向振动导致的预紧力下降率最大是4.5 N/周期，扭转振动导致的预紧力下降率最大是1.4 N/周期，因此，横向振动对螺纹连接松动的影响最显著。

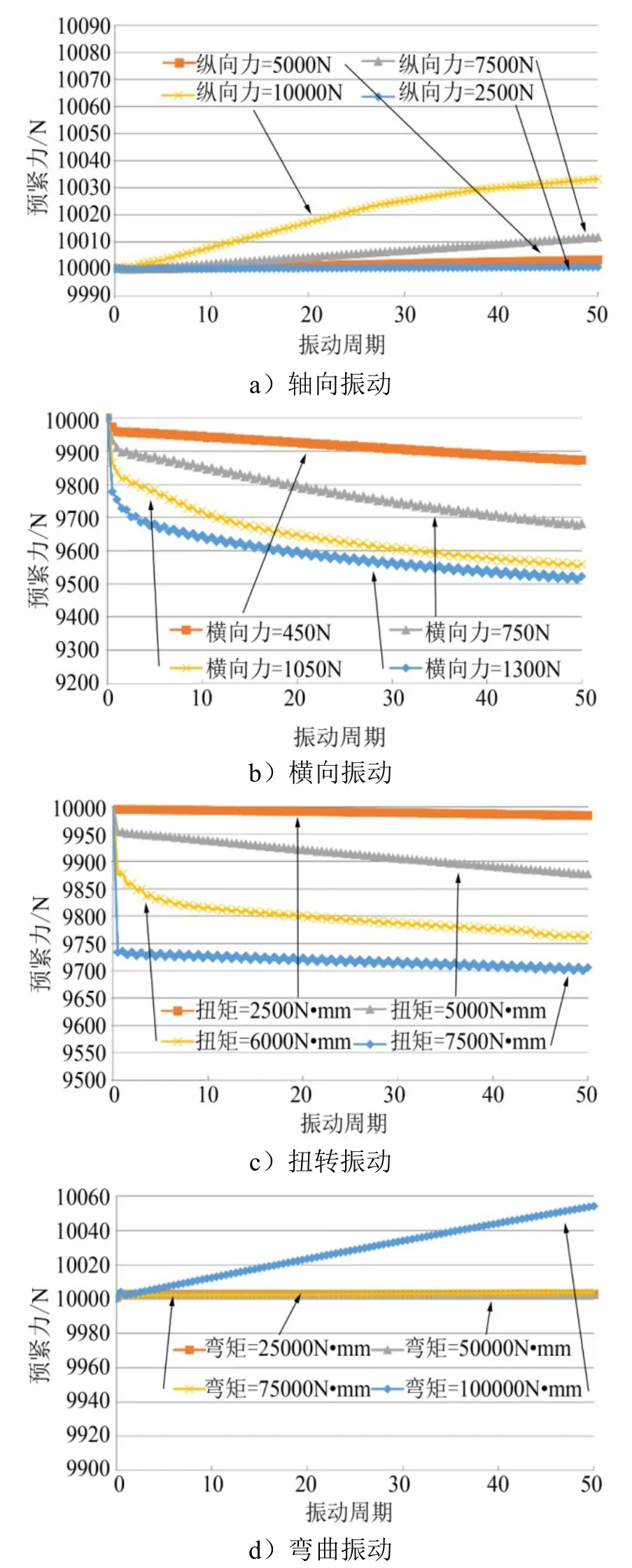
图7 不同振动载荷作用下螺纹预紧力随振动周期的变化趋势 Fig.7 Variation Trend of Thread Preload with Vibration Cycle under Different Vibration Loads

3.2 外部振动载荷耦合作用

首先将横向振动载荷分别与其他3种振动载荷耦合在一起，横向力是750 N，轴向力是5000 N，扭矩是5000 N·mm，弯矩是50 000 N·mm，振动周期是50，图8展示了不同耦合载荷作用下的预紧力变化情况。从图8a中可以看出，轴向振动几乎不会导致预紧力下降，相比于横向振动单独作用，横向振动和轴向振动耦合作用将导致更快的预紧力衰减。从图8b中可以看出，扭转振动和横向振动单独作用时都会导致预紧力下降，当二者耦合作用下，预紧力的衰减速度更快，衰减量几乎是它们单独作用的衰减量之和，这表明扭转振动和横向振动的作用几乎是相互独立的。图8c展示的预紧力衰减规律类似于图8a，即弯曲振动几乎不会导致预紧力衰减，相比于横向振动单独作用，横向振动和弯曲振动耦合作用将导致更快的预紧力衰减。综上，横向振动对螺纹连接松动起主导作用，轴向振动和弯曲振动单独作用不能导致螺纹连接松动，但二者和横向振动耦合作用将加剧螺纹连接松动，扭转振动也会导致预紧力衰减，它和横向力的作用几乎独立。

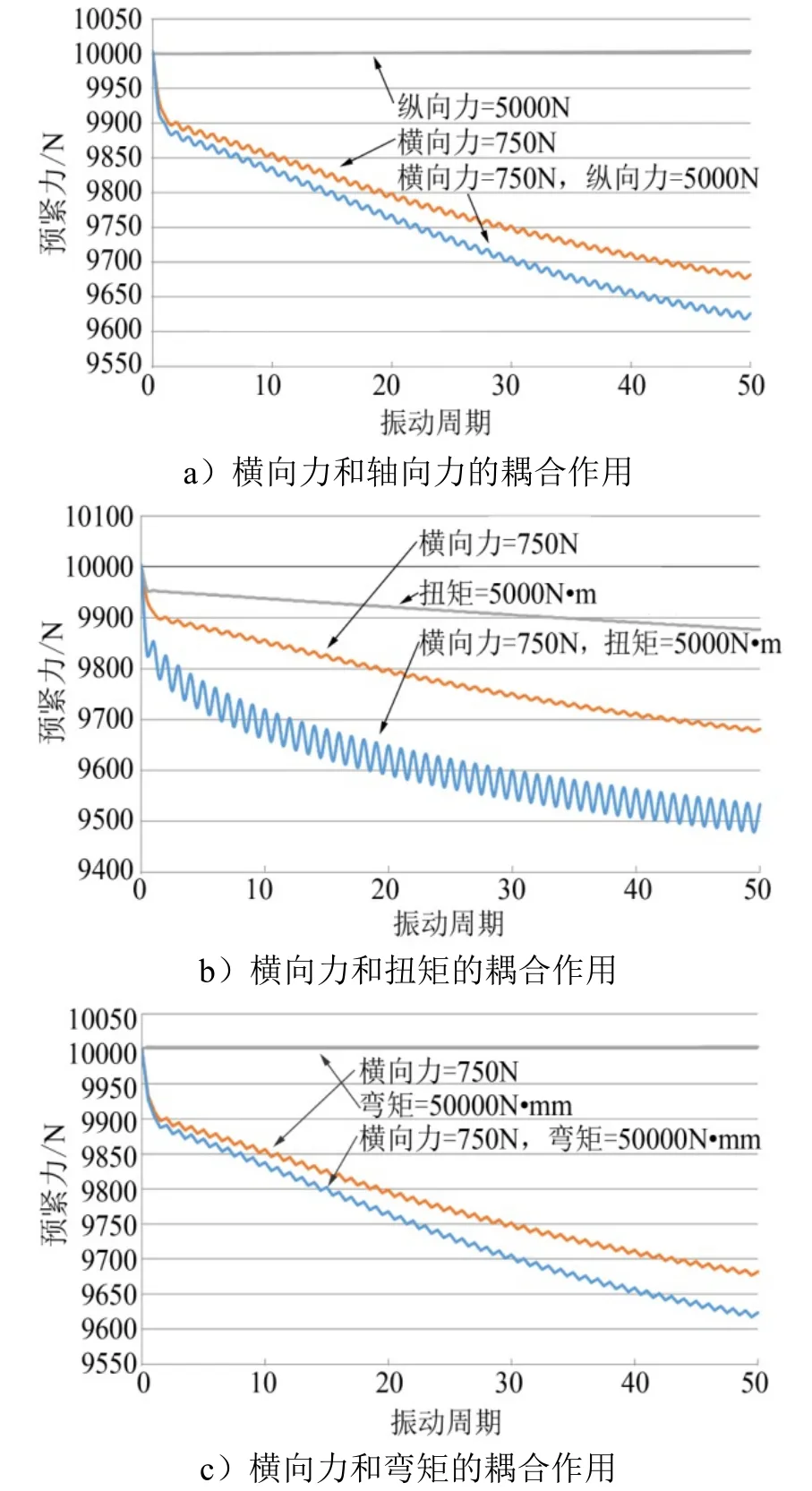
图8 不同耦合载荷作用下的预紧力变化情况 Fig.8 Variation of Preload under Different Coupling Loads

4 结 论

螺纹连接在恶劣的外部振动载荷条件下，极易引起松动从而导致螺纹连接失效，严重时会影响航天飞行任务成败。本文建立了螺纹连接的精确有限元模型，仿真了横向振动、轴向振动、扭转振动和弯曲振动的加载过程，分别研究了螺纹连接在4种振动载荷单独作用和耦合作用时的螺纹连接松动规律，得出以下结论：轴向振动和弯曲振动不能导致螺纹连接松动，扭转振动只有在特定的扭矩值时才能导致螺纹连接松动，横向振动则能导致严重的螺纹连接松动，其松动率远大于扭转振动导致的松动率。并且，当横向振动和其他3种振动载荷耦合作用时，横向振动对螺纹连接松动起主导作用。