体-翼连接干扰流动对局部区域气动热环境影响的研究

时晓天，高 军，赵 渊，赵 月，武健辉

（1. 中国航天空气动力技术研究院，北京，100074；2. 中国运载火箭技术研究院研究发展部，北京，100076）

0 引 言

随着高速飞行器的精准化设计，热防护/结构等系统设计对气动热环境的预测精度提出了更高的要求，尤其是对于驻点滞止区域和体-翼连接等局部干扰区[1～7]。

体-翼连接结构形式在飞行器气动布局中普遍可见，在高速条件下可引起复杂的局部干扰流动，引起高热流峰值，是热防护设计至今尚未完全解决的问题之一。与驻点区域的流动相对简单、存在较好的物理关系、能够较为精确地预测不同，体-翼连接的局部干扰流动区域，物理机制丰富、流动现象复杂且呈现高度的非定常性，激烈的有粘/无粘干扰可导致数倍于驻点或几十倍于无扰状态的局部热流峰值，严重威胁飞行器的热防护系统和飞行安全。如哥伦比亚号和X-15的飞行失事。

体-翼连接干扰流动，包含多种流动现象和物理机制[2～7]。翼/舵等几何部件带来的强逆压梯度，引起来流边界层的流动分离，干扰区内部伴随有粘/无粘干扰激波干扰、边界层转捩、强剪切、激波/边界层干扰、激波振荡等多种物理机制，波系变化、无粘/分离/再附激波和漩涡之间的相互作用等复杂的流动现象，最终改变了空间和边界层内部的物理量分布。这些复杂的现象是动态的和不稳定的。流动现象导致热流分布不仅在平均流场上呈现一定的空间分布，同时由于波/涡之间的相互作用，在时间上也存在较强脉动，引起热流的显著变化，给飞行器的热防护设计和预测带来严峻挑战。另外，体-翼干扰流动呈现明显的三维流动特征[7～9]。不同于前台阶或压缩拐角流动，体-翼干扰区在展向也存在较大的影响域和速度分量，强烈时可形成展向激波，进一步增加了流场的复杂度和气动热环境的预测难度。目前，对体-翼连接干扰流动影响局部气动热环境的物理机制还未形成深刻认识，存在参数影响规律不明确、预测精度偏低等问题。

本文针对体-翼连接干扰流动对局部气动热环境的影响机制和影响规律进行了梳理和介绍，系统阐述了流动特征、流动及几何参数影响，最后指出了可以深入开展的研究方向，为飞行器体-翼连接流动的热流预测及改进方向提供理论指导和技术支撑。

1 体-翼连接干扰的流动特征

自20世纪70年代以来，体-翼连接干扰流动对局部热环境的影响获得了重要关注。一般以平板+突起物的简化组合作为研究对象，突起物一般采用圆柱、钝翼、方柱等形式，典型干扰流场如图1所示，突起物的刻画参数包括，高度H、前缘直径D、后掠角Λ、倾角α等。

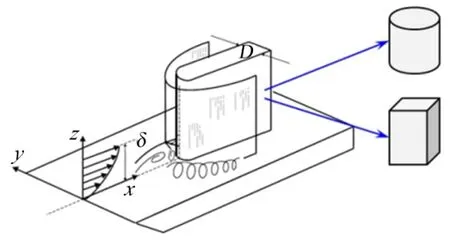
图1 体-翼干扰流动示意[8] Fig.1 Schematic Figuration of Body-fin Interaction Flow[8]

早期，主要通过试验手段获得平均流场的流动图像及热流的点测量数据[1～5,9]。在超/高速条件下：a）强烈的无粘效应在突起物前形成脱体的弓形激波；b）弓形激波与来流边界层相互作用导致流动分离，长度记为Lu；c）流动分离产生倾斜的分离激波，分离激波与弓形激波交汇形成激波/激波相互作用的“三波点”结构，对应高度记为htp；d）流动最终冲击到突起物表面，形成局部的高热流区域。Sedney，Doliing等对于不同高度突起物的研究结果表明，当突起物的高度h继续增加至三波点高度htp的2～3倍，流场特征不再发生变化，称为满足“渐近高度”，这一结论得到了普遍认可。分离区的长度、三波点的高度对于流场特征、热流分布和峰值具有重要影响。

干扰区内部由于流动分离与激波结构的共同作用，呈现出高度的三维和非定常特征。Sedney[2]针对满足渐近高度的组合流动，提出了“内区”、“外区”和“过渡区”的概念。他们在研究中发现，在外区，流动不受几何形式影响，流场具有相似性；内区的流动特征和热流分布受到多个参数的影响，在突起物根部存在高度的不稳定激波结构，导致压力信号呈现无明显周期的振荡现象。Korkegi在Ma=3的平板-钝翼组合流动中重复测量的壁面压力数据存在较大的散布，他们认为原因在于干扰区流动的非定常性。Dolling和Bogdonoff基于时序的纹影图像，发现在突起物的根部存在高度不稳定的激波结构，高频压力传感器测量的数据表明，存在大幅度的压力脉动，压力信号呈现非周期和宽频分布的特征。

2013年，Tutty，Roberts和Schurich[8]综合液晶热图的面测量技术、油流和数值模拟，针对Ma=6.7的平板-钝翼干扰流动开展了细致研究，得到了精细的流动特征和热流分布，尤其是激波和分离区内部的马蹄涡、突起物根部角区涡结构的分布特征。在分离区内部，超声速流动和局部压缩波导致流动在法向发生二次的流动分离和流动再附，产生一系列的马蹄涡结构；马蹄涡结构引起了热流分布的空间变化，在突起物前的平板表面形成非均匀的热流和压力分布。局部热流峰值存在于马蹄涡结构之间，对应于流动的法向分离和再附。

干扰区在展向存在一定的影响域，内区流动形成的流动结构同时向展向和流向发展，内区根部的不稳定激波结构，展向向外快速衰减。

近年来，体-翼干扰流动的研究逐渐由定性的认识过渡到定量的规律研究，由平均场发展到流动结构的发展过程及其对热流峰值的影响，研究趋于定量化和精细化[10,11]。

2 主控参数对流场和热流的影响

干扰区的流动分离及其对热环境的影响与几何参数、来流参数密切相关，包括突起物的高度、突起物形式、前缘直径、后掠角、倾角及马赫数、雷诺数、边界层流态等来流参数等。

2.1 几何参数影响

突起物的形式包括圆柱、方柱、钝翼等类型。李素循等的试验研究结果表明，不同形式的突起物均存在“渐进高度”的概念，即当高度增大到一定程度，干扰区域几乎不再过大；无后掠角情况下，方柱类突起物存在角区流动分离，引起的流动分离尺度约为圆柱情况的两倍；达到“渐进高度”以后，方柱对称面上的压力峰值与圆柱情况基本一致。潘宏禄等[12]开展了不同构型突起物的数值模拟，他们认为干扰区热环境分布与流动结构直接相关，方形头构件与圆形头构件对称面干扰区范围相差1.414倍（层/湍流均成立）。对于钝舵类突起物，在满足“渐进高度”的条件下，突起物上游的流场分布高度相似，钝舵的厚度或者前缘直径主要影响干扰区的展向分布，对流场特征及峰值热流的影响不明显[3,13]。

研究表明，引进突起物的后掠角能够有效减小干扰区的流动分离尺度。李艳丽等[14]的试验和数值模拟结果表明，在Ma=7.97的层流条件下，无后掠直立舵上游影响距离达到6倍的钝舵前缘直径（下文用D表示），即Lu=6D；后掠角45°情况时，干扰距离减至2D；当后掠角为67.5°时，对上游的干扰只有0.8D。增大后掠角能够有效的减小流动分离和抑制流动的非定常现象，对热流峰值也存在一定的改善。但数值模拟结果却认为热流峰值并无明显变化，Mortazavi等[15]在Ma=14条件下数值模拟得到的0°后掠及22.5°对称面上的热流曲线，两种情况下峰值热流基本相当，他们认为原因在于试验时，热流测点稀疏致使未捕捉到热流峰值。对此，尚需要进一步研究。

展向的倾斜角度主要改变干扰区的展向分布，对于固定状态，上游影响域或者最大分离区尺度与倾角无关，热流峰值基本一致。

2.2 来流参数影响

尽管已经存在大量的试验数据和研究工作，但流动参数对于体-翼干扰区气动热环境的影响，仍然存在许多不一致的认识：

a）马赫数、雷诺数对分离区长度影响。Korkegi的综述文章中认为分离区长度弱依赖于雷诺数、边界层厚度和马赫数；Dolling等认为分离区长度与马赫数的依赖关系并不明朗；Sedney认为分离区长度随马赫数增加而增大，Price和Stalling认为分离区随马赫数无明显变化。Lakshmanan和Tiwari[16]的数值工作认为，随着雷诺数增大，分离区的长度增大；随着马赫数的增大，分离区的长度减小。钝翼前分离区的涡结构数目同时依赖于来流马赫数和单位雷诺数。Hung和Buning在干扰流动的数值研究中，调整来流边界层的厚度变化一个量级，发现马蹄涡的尺度、干扰区的空间分布主要由无粘流动主导，弱依赖于雷诺数。Kolesnik和Smirnov认为雷诺数增大，倾斜压缩波的强度增大，分离区变薄，三波点高度减小、分离区长度增加，涡结构数目增多；进一步增大雷诺数，流动趋于不稳定，不可能得到稳定解。

b）层流状态下的分离区的长度。湍流状态下的认识较为一致；而层流状态下，Hung和Clauss的Ma=5.3试验结果认为突起物前的分离区长度Lu≈9～12D，Schuricht和Roberts[17]的Ma=6.7的试验结果中分离区的长度Lu≈8～9D，栗继伟等[18]在Ma=7.04的相似试验条件下的结果Lu接近4D，Tutty等在Ma=6.7条件下开展试验和数值模拟的研究工作，表明突起物前分离区的长度约为6.5D。

c）热流峰值大小及位置。Hung和Clauss对Ma=5.3的试验测量得到的层流状态下热流峰值Qmax/Qu约为100，湍流状态下约为20；而相近的层流流动条件下，Schuricht和Roberts的试验结果给出的Qmax/Qu＞10；栗继伟等中层流Qmax/Qu约为19，峰值热流位置在突起物前缘0.2D位置；俞鸿儒等Ma=6.6的试验结果，湍流状态Qmax/Qu约为31，峰值热流位置在突起物根部0.1～0.15D位置。峰值热流的大小和位置，可能与布置的热流传感器测点位置有关，也可能与流动的非定常作用导致的峰值热流位置变化相关，有待于进一步深入研究和确认。

综合试验研究，可以发现：a）来流状态对于分离区的长度具有重要影响，层流时分离区的长度Lu≈9～12D，湍流时Lu≈2～3D；b）流动分离明显的依赖于突起物的形式；c）后掠角度对于抑制流动分离作用明显，后掠角度增大到一定程度时，流动分离能够得到明显抑制；d）干扰区峰值热流远大于无扰动时的热流，无量纲幅值约为10～100倍无扰状态；e）马蹄涡的尺度、干扰区的空间分布主要由无粘流动主导，弱依赖于雷诺数。

3 体-翼连接流动的数值模拟技术

用于体-翼干扰区气动热环境的数值方法主要包括工程方法和CFD计算两种途径。

3.1 工程方法

经验公式的构建主要基于压力和热流之间的比拟关系：

式中Q，P分别为预测位置的热流和压力，P可以通过工程公式或者CFD方法获得；QU和PU为没有干扰物时该位置的热流和压力。一般认为层流时n=0.5，湍流时n=0.2。对于指数（1-n）根据不同的试验结果存在一定的调整。

压力比拟方法的基本观点是认为压力与对流气动加热存在一定的对应关系，在相似加热条件下，压力越大，气动加热也就越强。张学军和姜贵庆[19]给出了关系式成立的必要条件。黄志澄等[20]应用压力比拟方法建立了垂直天线干扰区气动加热预测半经验关系式，Michael等[21]则总结了前人工作给出了一系列外形下的干扰区热流预测方法。

近年来，CFD方法也开始应用到工程方法中的压力预测。

3.2 CFD数值模拟技术

最早的将CFD用于体-翼干扰流场模拟的是Hung和Buning在Ma=2.95的湍流状态下开展的平板+无后掠钝翼组合的数值研究，计算条件与Dolling和Bogdanoff的试验条件一致，数值模拟较好的预测了翼型驻点线和平板上的压力分布，但压力峰值被严重低估，原因被归结为网格分辨率不足。

Tutty等[22]开展了平板+钝翼组合的RANS数值模拟，计算方法为有限体积法。他们将数值模拟结果与Haq，Roberts和East[23]的Ma=6.2的试验结果进行了对比。数值计算得到的热流分布规律与流场特征现象比较符合，但峰值热流的位置比试验结果靠前。他们认为原因为网格分辨率不足，同时他们指出：a）对于干扰区的数值模拟，要求算法对于间断具有较好的捕捉能力；b）计算热流需要预测温度的导数，比压力的预测更加具有挑战性。

Lakshmanan和Tiwari采用有限体积法研究了层流状态下，马赫数（1.2，2.36，3.5）和雷诺数（1.25e6，2.5×106，5×106）对平板-钝翼组合的流动影响。研究表明，数值模拟预测的分离区的长度偏小。

Houwing[24]开展了层流状态下平板-钝舵干扰流动的数值模拟研究，考察高焓条件对于干扰流动影响，数值结果较好地预测了分离区的流动特征，但预测的弓形激波脱体距离低于试验结果，原因可能是CFD计算中采用固定的理想气体的比热比，与试验中多组分的影响差异。

Tutty等人的有限体积数值模拟给出了流场中的流动结构特征和热流分布的结果对比，但仍然存在以下差异：a）数值预测的弓形激波的脱体距离低于试验结果；b）试验结果得到的分离区长度约为6.5D，低于Huang和Clauss在Ma=5.3层流条件下的9～12D。

Mortazavi和D.Knight采用有限体积法开展了Ma=14层流状态下的平板-圆柱前缘钝翼组合的数值模拟，考察了后掠角度对于干扰流场的影响。认为后掠角能够有效的减小分离区、抑制流场的非定常效应；但热流峰值与后掠角度无关，约为5倍驻点热流强度；垂直圆柱的热流数据存在周期性振荡。

Kolesnik等[25]基于有限体积法的数值模拟工作汇报了Ma=6.7、Re=1.25×106、1.56×106条件下平板-钝翼干扰流场中的马蹄涡数目和尺度存在双解的现象。Kolesnik和Smirnov[26]开展了超声速（Ma=5）层流状态下的平板-钝体组合的有限体积法的数值模拟。得到了影响参数如马赫数、雷诺数、温度因子、平板长度对流动结构和传热的定性和定量的影响规律。在所有考察状态，流场基本相似，大的分离区、弓形激波和经过分离区形成的斜的压缩波；增大雷诺数和减小马赫数均使得流动趋于不稳定、分离区长度增加、马蹄涡结构数目增多；不同参数下的热流峰值基本相当。

中国也积极发展CFD方法用于局部干扰区的气动热环境预测。1993年，邓小刚和张涵信[27]采用NND格式研究了Ma=4.9的平板-方舵组合的气动热环境预测，揭示了流场的非定常现象。2015年，潘宏禄等[28]基于有限体积法开展了Ma=6的平板-小尺度圆柱组合的大涡模拟，获得了流动结构的空间分布及粗糙元尾迹的发展过程。刘哲等[29]基于有限体积法的RANS求解了平板上钝舵与单股喷流耦合的数值模拟，发现了组合干扰流动的两种不同的耦合状态。

近年来，高精度数值模拟技术开始应用到局部干扰流动机理研究中来，如RANS/LES混合方法[30]、WENO方法[31]、高精度有限体积法[32]。

4 结束语

本文在针对体-翼干扰流动对局部气动热环境的影响，整理了体-翼干扰流动的研究进展，分别对流动特征、参数影响和数值方法进行了总结，并对体-翼干扰流动进行了总结和分析。

对体-翼连接干扰流动，研究工作逐渐由流动机理由定性趋于定量化，由单一手段的简单认识过渡到多种研究手段综合运用的精细化研究。定性的图像能够达成共识，但存在参数影响规律不清晰、非定常过程研究不充分、分离区长度和热流峰值偏差较大等现象，难以对工程设计形成有效的理论指导。数值模拟和风洞试验方面还存在很多相互不一致的认识，有待于综合多种风洞试验测量技术和高精度的精细化数值模拟技术深入研究。此外，在干扰机理和参数影响规律的研究基础上，还应开展优化设计和局部修型研究工作，更好地为热防护提供技术支持。