尖化前缘局部稀薄气体效应对气动热影响研究

高莹莹，陈政伟，谢 飞，赵小程，杨凯威

（北京航天长征飞行器研究所，北京，100076）

0 引 言

随着洲际导弹、返回式卫星、载人飞船和航天飞机的研制，飞行器在稀薄气体中飞行的时间越来越长，高度在80～100 km的空气密度大约只有海平面的1/106～1/105，飞行器处在稀薄气体环境之中，高空、低密度带来的稀薄气体效应已经开始显现为了获得较好的气动性能，目前先进飞行器的前缘应具有尖化的边缘，局部小尺寸外形也同样是稀薄气体效应产生的契机。

理论研究方面，王智慧等开展了多项尖化前缘稀薄气体效应理论研究[1～3]，黄飞等分析尖化前缘稀薄效应对热流的影响[4]，戎宜生等开展了过渡流区圆柱体驻点热流的工程计算[5]，欧吉辉等进行了有局部稀薄气体效应的流动数值模拟[6]；试验研究方面，陈星开展了不同球头半径的驻点热流实验测试[7]，吴松等开发了小型化的热流传感器[8]。但目前尚未开展前缘半径小于2 mm的尖化前缘热环境研究。

判断不同气体稀薄程度的相似参数为克努森数（下文称Kn数），其定义为分子平均自由程λ与流动特征尺度L的比值。尖前缘飞行器在近空间大气层飞行时，由于飞行器本身尺寸较大，所以从整体Kn数判断，整体上还处于连续流区域，但是由于尖前缘的曲率半径很小，且驻点附近流场梯度很大，在局部区域内，流场的特征尺度很小，致使该区域Kn数很大，稀薄气体效应显著。而这一局部区域，正是飞行器设计中气动加热最严重的驻点附近区域，因此有必要引入当地Kn数或局部Kn数的概念，记为Knlocal，其定义为

式中Q可以为温度、密度等；l为流场中两点间的距离；Knlocal由于考虑了流场中某一点的当地分子平均自由程和当地流场梯度大小，因此更能精确地刻画流场的当地稀薄程度。

随着Kn数的增加，稀薄气体效应越来越显著。对于大尺寸外形，稀薄气体效应增加的主要因素在于飞行高度的增加带来的分子平均自由程λ的增大，对于尖锐外形等局部小尺寸外形，由于特征尺度减小，在较低的飞行高度下也会出现局部稀薄气体效应。

本文对飞行器尖化前缘外形进行测热试验，获得前缘半径分别为0.5 mm、2 mm和5 mm 3种小尺寸前缘半径尖化前缘中心线热流分布规律，分析在半径较小的情况下的局部稀薄气体效应。并通过高空稀薄过渡区的热环境预测方法与试验结果进行比较，评估稀薄气体效应对气动热环境的影响。

1 尖化前缘风洞测热测压试验

1.1 试验模型

由于飞行器外形头部附近的热流最高，因此试验截取头部附近长为650 mm的区域作为尖化前缘理论外形。为比较不同尖化前缘半径的热流分布规律，研究局部稀薄气体效应，在理论外形的基础上修改前缘半径，加工3组前缘半径R分别为5 mm、2 mm、0.5 mm的尖化前缘外形作为试验模型。模型安装在风洞中如图1所示。

图1 试验模型 Fig.1 Model at the Wind Tunnel

1.2 试验状态

本次试验在中国科学院力学研究所高温气体动力学国家重点实验室JF8A和JF10风洞中进行，试验的流场状态参数见表1，试验攻角均为0°。

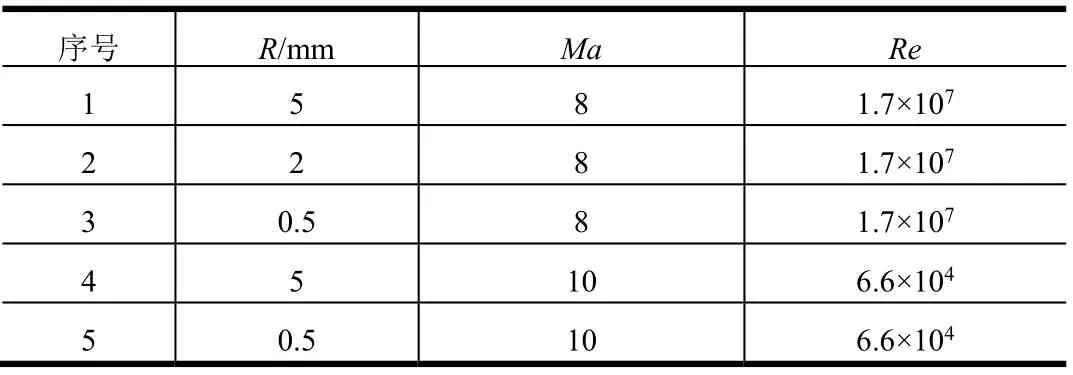
表1 试验状态参数 Tab.1 Experiment Condition

1.3 试验结果

分别对表1的5种试验状态进行了测热测压试验。试验测得的驻点热流如表2所示。

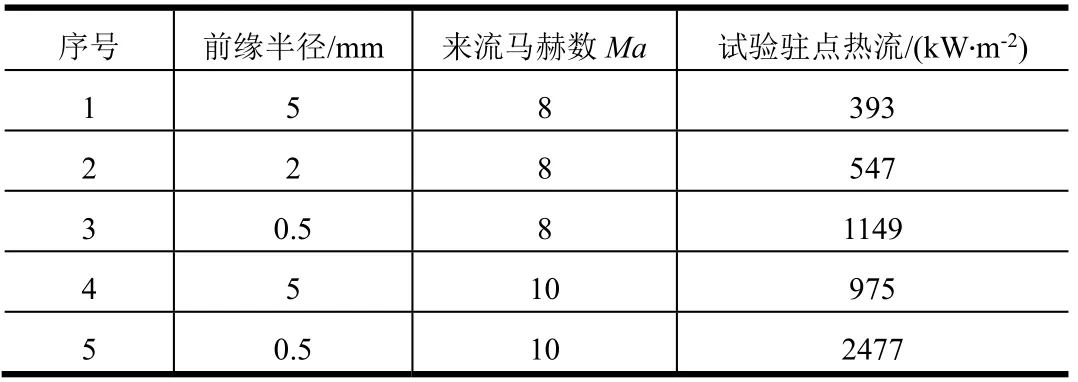
表2 驻点热流试验结果 Tab.2 Experiment Stagnation Heat

5种状态的尖化前缘中心线无量纲热流（均以驻点无量纲化）分布比较如图2所示，可以看出分布基本一致，均在驻点至50 mm处下降到50%以下。

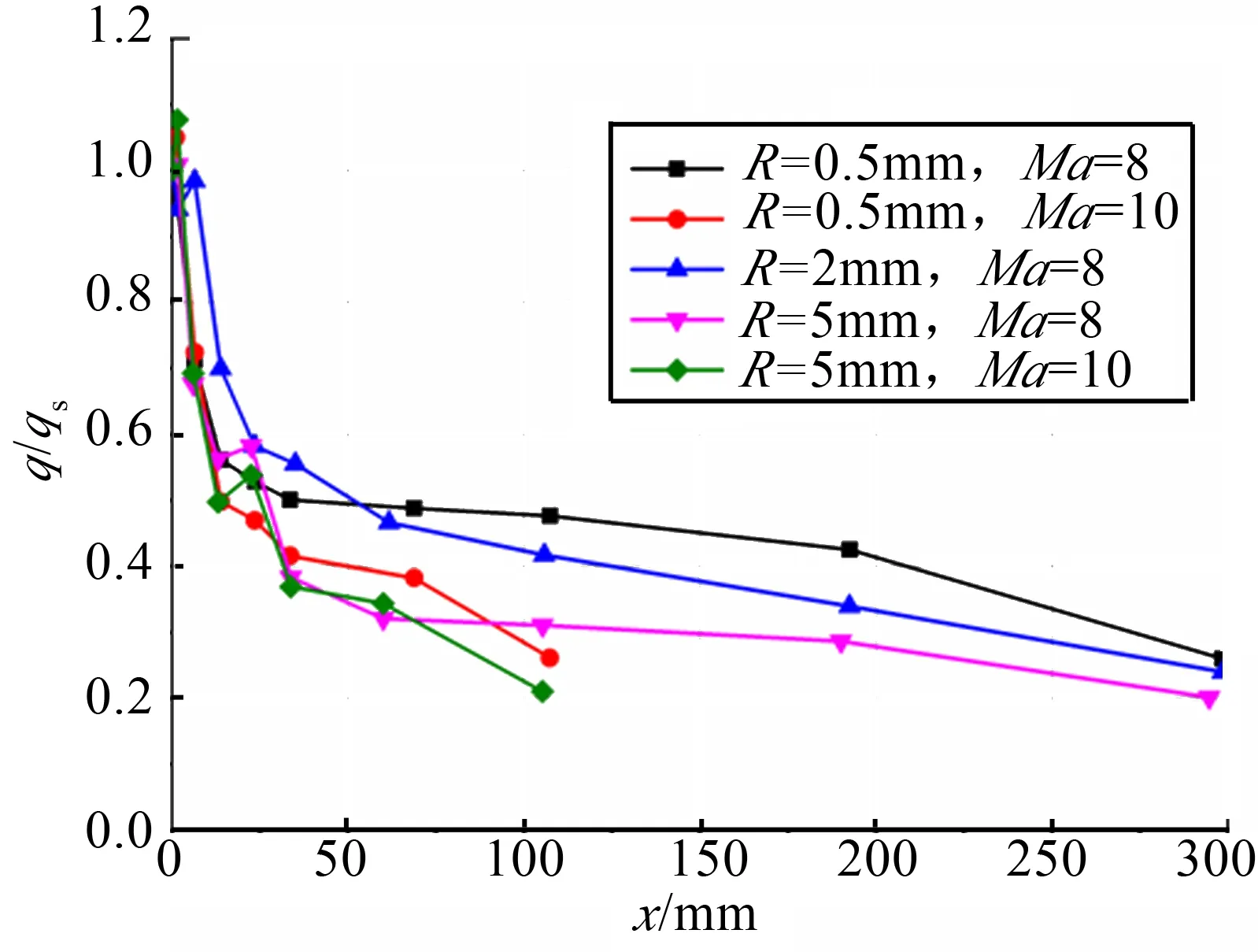
图2 前缘中心线无量纲热流分布 Fig.2 Leading Edge Nondimensional Heat

2 尖化前缘稀薄气体效应研究

2.1 驻点热流公式适用性研究

三维球头驻点热流常用的Fay-Riddell公式为

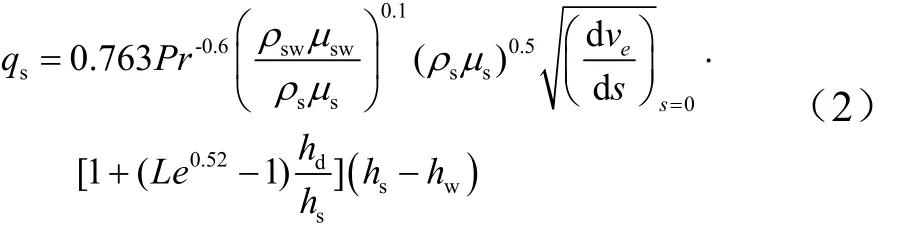
式中qs为驻点热流；Pr为普朗特数；ρsw为壁面气体密度；μsw为壁面气体粘度；ρs为驻点气体密度；μs为驻点气体粘度；ve为边界层外缘速度；s为沿母线长度；Le为刘易斯数；hd，hs，hw分别为离解焓、驻点焓、壁面焓。

为了验证Fay-Riddell驻点热流计算公式在半径非常小的情况是否能够适用，需要通过Fay-Riddell公式和试验测量结果进行比较。计算结果与试验结果比较如表3所示。当半径R=0.5～5 mm、Ma=8时，驻点热流与Fay-Riddell公式值偏差小于10%；当半径R=5 mm、Ma=10时驻点热流与Fay-Riddell公式值偏差依然小于10%；但当半径R=0.5 mm、Ma=10时驻点热流低于Fay-Riddell公式值29.5%，说明此状态下外形存在局部稀薄气体效应。随着外形尺寸减小和稀薄程度的增加，Fay-Riddell公式计算结果与试验值差别增大，在小尺寸下已不再适用，需要考虑局部稀薄气体效应对气动热的影响。

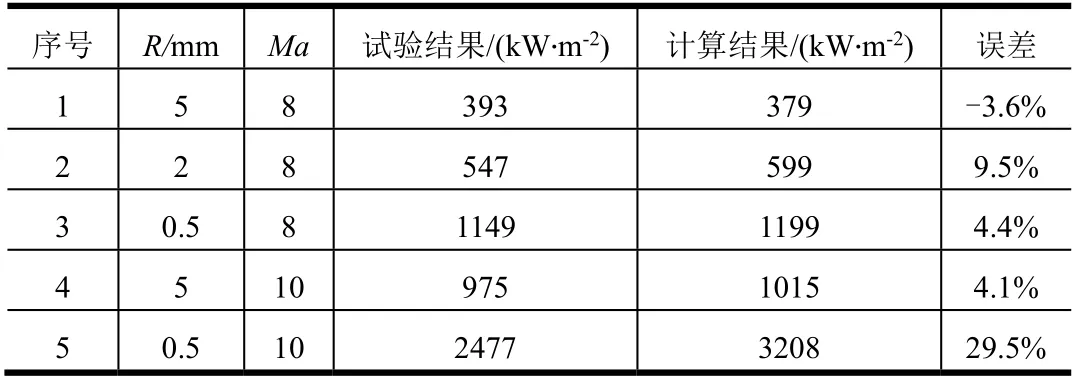
表3 驻点热流结果比较 Tab.3 Comparison of Stagnation Heat

2.2 局部稀薄气体效应计算

钱学森根据Kn数范围，将流动划分为连续流、滑移流、过渡流、自由分子流，其中连续流和滑移流为连续流区，过渡流和自由分子流为稀薄流区，划分标准如下[9]：

a）连续流领域（Kn＜0.01），符合连续介质假设，可以用N-S方程描述；

b）滑移流领域（0.01≤Kn＜0.1），物面滑移边界条件，需要求解滑移边界条件下的N-S方程，工程上可将滑移流合并到连续流；

c）过渡流领域（0.1≤Kn＜10），滑移流区的上限和自由分子流的下限之间的区域，从理论上难以处理，常用DSMC方法计算[10,11]，工程上常利用连续流和自由分子流结果，采用桥函数加权平均；

d）自由分子流区（Kn≥10），采用无碰撞项的Boltzmann方程[12,13]，工程上使用简化的热流计算方法。

自由分子流区热流密度计算工程计算方法如下：

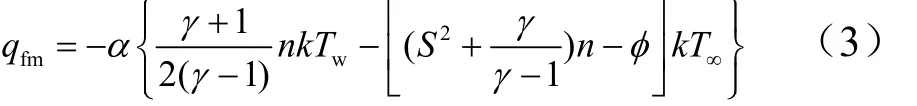
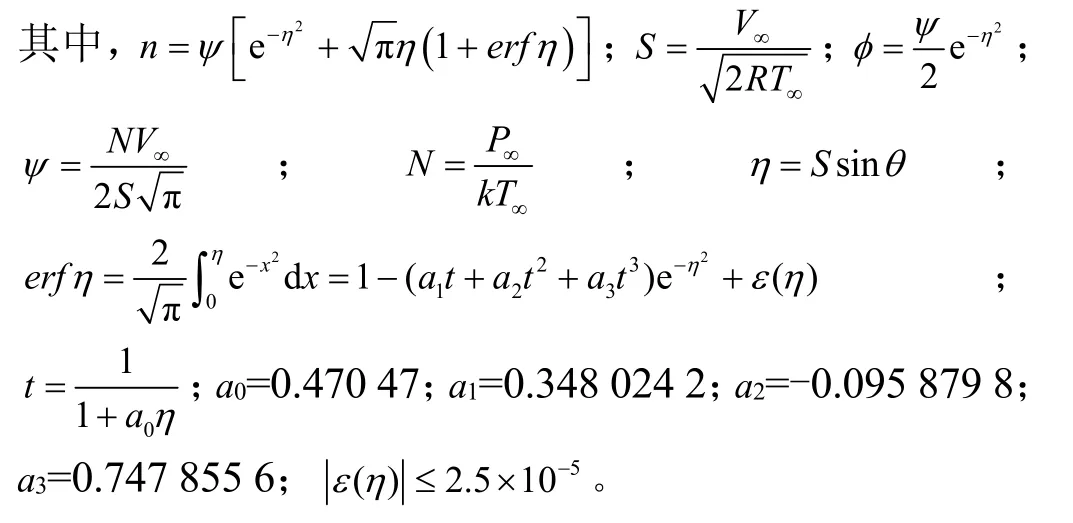
式中α为适应系数；θ为气流与物面夹角；k为玻尔兹曼常数；R为理想气体常数；P∞为自由流压力；T∞为自由流温度；V∞为自由流速度；Tw为壁温。

过渡区热环境计算首先计算连续流假设下的热流qc，再计算自由分子流假设下的热流qfm，最后采用桥函数方法进行搭接。通常采用Matting桥函数[14]、Nomura桥函数[15]、线性桥函数方法计算过渡区热环境。其中Matting桥函数方法如下式：

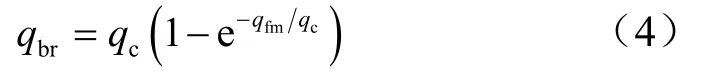
采用Matting桥函数计算前缘半径分别为5 mm、 2 mm、0.5 mm的尖化前缘外形Kn数以及过渡区热流与热流测量值及Fay-Riddell公式比较如表4所示。

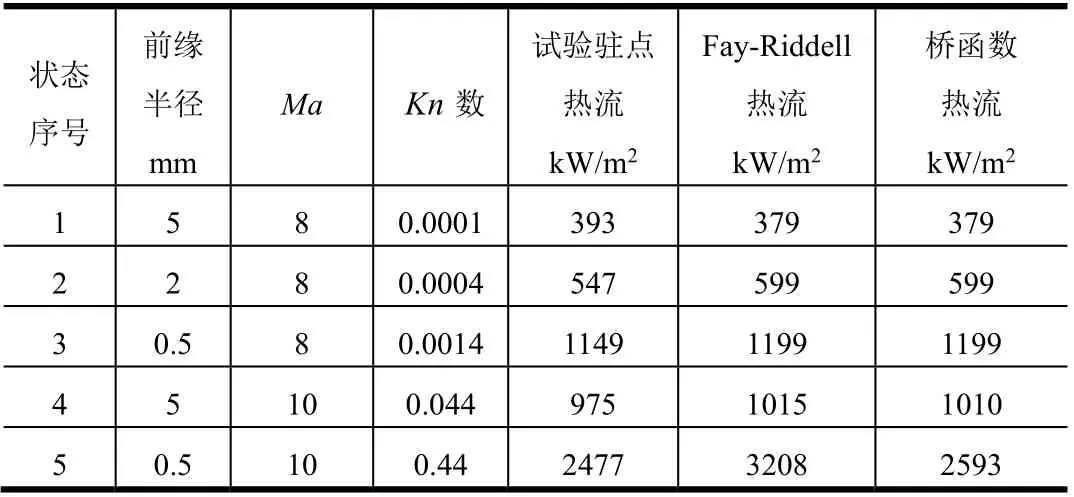
表4 热流测量值与Fay-Riddell公式及桥函数结果的比较 Tab.4 Comparison of Stagnation Heat between Experiment、 Fay-riddell Formula and Bridge Function

由表4可以看出，随着前缘半径的减小，Kn数越大，流动稀薄程度越高。Ma=8条件下不同前缘半径对应的Kn数均小于0.01，流动仍属于连续流，局部稀薄气体效应并不明显。Ma=10、R=5 mm时，Kn数在0.01～0.1之间，流动状态属于滑移流；Ma=10、R=0.5 mm时，Kn数在0.1～10之间，流动状态属于过渡流。因此R=0.5 mm出现局部稀薄气体效应，采用桥函数搭接方法计算的热环境与实际测量结果符合的较好。考虑稀薄气体效应后的实际热流比连续流计算的偏小，这对热防护是有利的。

3 结 论

通过研究得到如下结论：

a）对于较小尺寸的尖化前缘飞行器，在80 km以下的高度已经出现了局部稀薄气体效应，并且局部稀薄气体效应随着尖化前缘球头半径的降低和高度的增大变得更加显著；

b）桥函数计算过渡区热环境结果与试验结果符合较好，考虑稀薄气体效应后的实际热流比连续流计算的偏小。

综上所述，对于气动热环境的工程评估，当出现高度增大或局部尺寸减小时，有必要考虑稀薄气体效应，需要采用桥函数进行稀薄过渡区的热环境预测，以便更加准确地评估稀薄气体效应对气动热环境的影响。