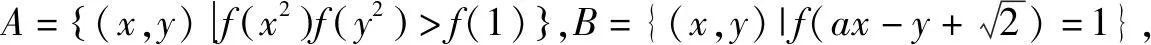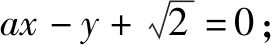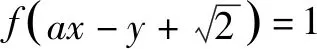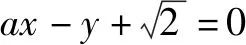三类抽象函数常考题型例析
厦门集美中学 陈习俭
1 f(x+y)=f(x)+f(y)型
求最值问题是有关抽象函数问题常见的一类题型,需要根据函数的自身基本特征求解,例如f(x+y)=f(x)+f(y)类型的抽象函数,可以先构建一次函数(f(x)=kx)进行转化:①分析函数f(x)的原型解析式,以及该函数的周期性、奇偶性、单调性等;②利用f(x+y)=f(x)+f(y)等基本特征求解,通过构造不等式判断函数在定义域内的单调性;③具体问题具体分析,结合所知条件得到所求最值.
例1对任意的x,y∈R,函数f(x)均满足f(x+y)=f(x)+f(y),并且当x<0时,有f(x)>0,f(1)=-3,求函数f(x)在区间[-2,3]上的最大值和最小值.
分析:本题是很明显的一次函数型抽象函数问题,其中f(x)的原型是y=-3x.猜想该函数是实数集R上单调递减的奇函数,要求解在区间[-2,3]上的最值,即分析f(-2),f(3)的值.
解:根据题意,得f(0)=0,f(-x)=-f(x),f(2)=2f(1)=-6,f(3)=3f(1)=-9.
令任意x1 f(x1)-f(x2) =f[(x1-x2)+x2]-f(x2) =f(x1-x2)+f(x2)-f(x2) =f(x1-x2). 依题意,由x1-x2<0,得f(x1-x2)>0. 即有f(x1)>f(x2). 所以f(x)在区间[-2,3]上是减函数. 故它的最大值为f(-2)=-f(2)=6,最小值为f(3)=-9. 分析:由于一次函数满足f(x+y)=f(x)+f(y),可假设函数f(x)=-kx,借助已知条件f(1)=-2求出具体函数解析式,判断所得解析式是否满足“当x>0时,f(x)<0”这一条件.最后将所求一次函数解析式代入命题中的不等式中,求出具体解集,即可判断命题的真假. 解析:设函数f(x)=-kx. 由f(1)=-2,可得k=2. 即f(x)=-2x,且满足x>0时,f(x)<0. 代入不等式,可得-6x2+4x<-6x+4. 整理,得6x2-10x+4>0. 故所给命题为真命题. 求自变量的值是抽象函数问题的另一类常见题型,也需要利用其函数基本特征求解,例如f(xy)=f(x)f(y)特征类抽象函数,可以构建幂函数型(f(x)=xn)特征函数进行转化,需要遵循以下思路:①猜想具体函数解析式,根据题设信息分析函数的具体形式,例如f(x)=x-1等;②根据猜想的函数形式判断对应函数的单调性,并利用单调性解题;③利用函数基本特征解题,即将f(xy)=f(x)f(y)等基本特征与实际问题相结合进行求解. 解:根据题意可知 所以f(x)在区间(0,+∞)是减函数. 又因为f(1)=f2(1),f(x)>0,所以f(1)=1. 又f(m)f(3)=f(3m),所以f(3m)=1=f(1). 变式2已知f(x)在(0,+∞)上都有f(x)>0,且满足f(xy)=f(x)f(y),f(3)=27,若f(-a2)=-64,则求a的值. 分析:猜测满足条件f(xy)=f(x)f(y)的函数f(x)为幂函数型,则假设f(x)=xn,利用该条件与f(3)=27推断函数f(x)的解析式,并判断函数的奇偶性,然后由f(-a2)=-64,即可得到a的值. 解析:假设函数f(x)=xn. 由f(3)=27,可得f(x)=x3. 则有f(-x)=-f(x). 所以f(-a2)=-f(a)f(a)=-64. 因此f(a)=8,故a=2. 抽象函数问题常见的还包括证明不等式成立问题,利用其函数基本特征是求解的常规手段,例如形如f(x+y)=f(x)f(y)的抽象函数,可以构建指数函数型[y=ax(a>0,a≠1)]特征函数进行转化:①确定函数的解析式,即由题设信息分析得到函数的具体形式,例如y=a2等;②判断函数的单调性,即根据函数解析式和题设条件,猜测函数在对应定义域内的单调性;③利用函数基本特征分析求解,即结合已知条件和函数的基本特征如f(x+y)=f(x)f(y),解得所求值. 例3已知函数f(x)对任意x,y∈R,都满足f(x+y)=f(x)f(y),且当x>0时,有0 分析:首先结合题意得到y=e-x是函数f(x)的原型,从而猜测f(x)是减函数,再利用指数函数的基本特征f(x+y)=f(x)f(y)分析,得到0 证明 :依题意,得f(1)=f(1+0)=f(1)f(0). 又f(1)>0,所以f(0)=1. 所以f(0)=f[x+(-x)]=f(x)f(-x)=1. 当x<0时,则-x>0,0 故f(x)>1. 综上所述,当x<0时,f(x)>1. 证明:因为当x>0时,0 f(x2)f(y2)=f(x2+y2)>f(1). 因为函数f(x)在R上单调递减,所以 x2+y2<1. 故集合A代表圆面x2+y2<1内点的集合. 因为f(1)=f(0+1)=f(0)f(1),且f(1)>0,所以 f(0)=1. 由上述三个案例及其解题思路可以发现,对于有关抽象函数问题,首先需要根据题意构建对应函数类型,然后分析函数单调性,再利用对应的基本特征求解.因此一定要仔细分析题意,并熟悉各类函数的形式和性质,确保求解方向正确.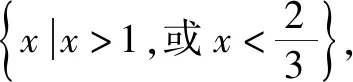
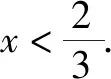
2 f(xy)=f(x)f(y)型
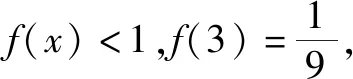
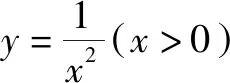
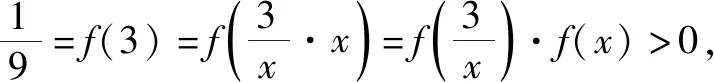



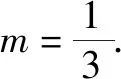
3 f(x+y)=f(x)f(y)型