基于创新思维培养的高考数学微专题设计
——以“解三角形中最值问题”为例
陕西省西安惠安中学 龙正祥
1 高考动向分析
解三角形问题可以较好地考查三角函数的诱导公式、三角恒等变换、三角形边角转化、正余弦定理等知识点,是三角函数、解析几何和不等式知识的交汇点,在高考试卷中大题基本上隔年出现,小题则是年年必考.全国卷及新高考卷在2020年、2021年均有考查,处理解三角形中的最值问题主要有两种方案,一是建立目标函数后利用基本不等式解决,二是建立目标函数后利用三角函数的有界性解决.
2 教学目标设置
(1)在熟悉的情境(素材1、素材2)中,通过问题引入,逐步提炼出从数(构建不等式、函数、方程等模型)和形(寻找特殊位置、临界位置)两个角度解决取值范围问题的一般方法,培养学生的解题能力,发展数学抽象、直观想象、数学建模等素养;
(2)在较复杂的情境(合作探究)中,通过变式延伸、对比分析,逐步提炼出求最值的一般思路:建立模型→二元函数(基本不等式)→化归转化→一元函数(单调性)→问题解决,提升学生的逻辑思维能力,发展逻辑推理素养;
(3)在具体情境中熟练运用正弦定理、余弦定理、面积公式等建立模型,通过三角恒等变换、三角函数的有界性、基本不等式等求解模型,提升学生的运算求解能力,发展数学运算素养.
3 教学重难点
重点:在具体情境中会从数的角度,通过构造不等式、方程、函数解决取值范围问题;在具体情境中会从形的角度,通过图象的特殊位置、临界位置探寻最值问题所表达的图形语言.
难点:如何更好地从学生角度分析解决问题.
4 教学过程
4.1 自主学习,寻找创新思维素材
素材1(北师大版必修五第52页A组第5题)已知锐角三角形的边长分别为1,2,m,则实数m的取值范围为.
师:大家对这道课本上的题都很熟悉吧!请同学们分享一下你是如何探寻实数m的取值范围的.(举手同学有4人)
生1:由两边之和大于第三边,两边之差小于第三边,可得实数m的取值范围为1 师:好,该同学很快就找到了限制m的不等式. 生2:不对,他没考虑锐角,这是锐角三角形! 师:这位同学读题非常仔细,给你点赞,那你补充一下! 生2:因为是锐角三角形,所以每个角的余弦值都大于零,可由余弦定理得到限制实数m的不等式.不妨设A,B,C的对边分别为1,2,m,则由余弦定理得 师:非常棒!如果我们观察第一个式子,它是恒成立的!理论实践相统一,简洁就是数学美! 师:这三位同学做得非常好!他们从数的角度利用余弦定理构造了关于限制实数m的不等式,还有其他思路吗? 师:厉害!从形的角度考虑问题所表达的特殊图形,利用数的最值就是形的特殊位置的思想巧妙地化解了问题,四两拨千金,数形结合真精妙! 设计意图:用学生熟悉的情境,激发学生创新思维意识,引导学生从“数”和“形”两个角度思考取值范围问题,初步感知到从数的角度就是构造不等式,从形的角度就是寻找特殊图形.同时复习巩固“已知三角形三边,首选余弦定理”以及锐角三角形的限制条件,强化双基. 素材2(北师大版必修五第52页B组第1题)在△ABC中,a=x,b=2,B=45°,若△ABC有两个解,则x的取值范围为 ( ). A.(2,+∞) B.(0,2) 师:此题我们又该如何从“数”和“形”两个角度分析呢?请同学们先认真思考,同桌之间可以交流,3分钟后分享. 生5:我们两个(同桌交流)的思路是利用正弦定理,通过建立函数来解决. 师:同学们今天表现都非常棒,相互帮助共同进步.谁还有其他想法? 生7:还可以用余弦定理,通过建立方程,差不多也能解决,但是答案好像不对. 师:差不多!不确定!好像还是蛮有思路的,展示给大家,我们一起分析,共同解决. 师:同桌能分析一下这样解的原因吗?(大多数同学很懵) 师:至此,我们看到了这个取值范围问题可以直接建立不等式来解决,也可以通过构建函数模型,转化为求函数值域的问题,还可以通过建立方程模型,转化为研究方程解的问题. 师:非常棒!从图形的角度解读取值范围问题,形象直观. 设计意图:本素材的探究,诠释了从“数”的角度解决取值范围问题时可以直接建立不等式来解决,也可以通过构建函数模,转化为求值域问题,还可以通过建立方程模型转化为研究方程解的问题;从“形”的角度通过特殊图形、特殊位置解决取值范围(最值)问题.如果上升到解决取值范围问题的方法论角度,本素材只不过是以解三角形为背景,如果换作其他知识模块,解决取值范围问题的思路、思想方法都是不变的. 师:请同学们分小组研究讨论,注意提炼解决二元变量取值范围问题的常规思路.抽小组进行展示,讲解. 由正弦定理,得 展示2:利用余弦定理a2=b2+c2-2bccosA,得 3=b2+c2-bc. 另一方面,由三角形的面积恒大于零,得 设计意图:通过延伸让学生再次体会“边化角”“角化边”解三角形问题的常规思路,化成边可以利用基本不等式解决最值,如果化成角可以利用三角函数的图象、性质解决最值问题,拓展学生思维,巩固基本不等式、三角恒等变换、三角函数等相关知识. 变式1条件不变,试求三角形△ABC周长的取值范围. 分析:本题由基本不等式只能求出一边范围,容易忽略构成三角形的条件,即两边之和大于第三边. 展示3:由正弦定理,得 展示4:利用余弦定理,得3=b2+c2-bc. 整理,得3=(b+c)2-3bc. 另一方面,由三角形的两边之和大于第三边,得 设计意图:通过变式让学生继续感受当问题变为“边”的问题时如何解决,引导学生利用化归思想转化为角的问题;另一方面,引导学生结合题目特点,利用余弦定理、重要不等式求解,同时也可以“边化角”直接利用延伸题的思路解决. 变式2条件不变,试求sinB+sinC的取值范围. 展示6:由正弦定理,得 设计意图:在具体情境中,培养学生的创新思维、发散思维,提升学生对问题的转化能力. (1)范围问题解答思路 思路1:数的角度——构造不等式、函数、方程. 思路2:形的角度——寻找特殊位置、特殊图形. (2)最值问题求解策略 思路1:建立函数——利用单调性、有界性. 思路2:基本不等式——寻找等量关系. (3)解三角形知识体系 基本理论——内角和、三角形分类、面积公式等. 定理——正弦定理、余弦定理. 设计意图:通过归纳总结,提炼思想方法,明晰知识技能,构建知识思维导图,为学生后续的深度学习提供可能素材. 设计意图:立足课堂教学,巩固“四基”“四能”,让所有学生都能体会到课堂上所学知识对自己做题有很大帮助;同时也看到了新高考在解三角形这一模块的命题思路,为其他模块的学习提供思路和方法. ①求B;②若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围. 设计意图:为学有余力的学生搭建再发展的平台,进一步理解取值范围问题解答的通性通法,为广义取值范围问题的解答提供思考空间,真正落实高考复习备考的主导思想.基础知识是明线——通过复习检验知识点有没有完全掌握;思想方法是主线——能不能站在思想方法的高度认识问题;核心素养是暗线——问自己核心素养有没有得到质的提升. 本节课设计立足学生实际,取材课本、真题,依据课标、高考评价体系,注重学生创新思维的培养,渗透了学科核心素养.在整节课的设计中,运用了自主学习、合作探究、反思悟道、目标检测四个学习环节,引导学主动参与学习,帮助学生在掌握四基、提升四能的基础上,学会学习数学. 通过学生熟悉的情境,立足基础,从引例出发,通过一个个变式,为后面的合作探究提供了活动经验,激发了学生的学习兴趣,让学生看到高三复习就要立足基础,注重思维,注重思想方法. 本节课所涉及的知识内容较多,从解三角形、三角函数再到基本不等式,有计算,有画图等,再加之是公开示范课,课堂节奏较快,基础薄弱的学生某些环节做得不到位.因此,教学中容量要适当小一点,思维深处要放慢一点,让更多的学生体会数学的产生、发展、变化过程.
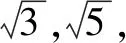

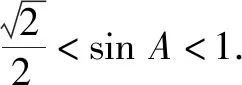

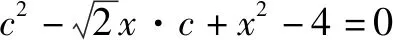
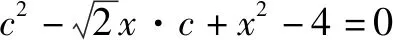
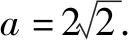
4.2 合作探究,培养创新思维品质
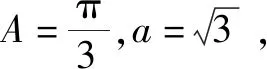
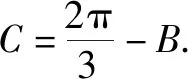

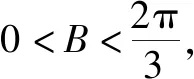
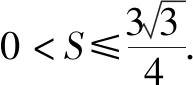
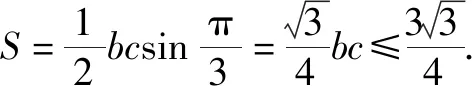
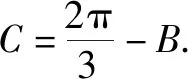
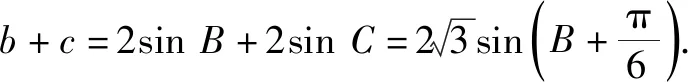
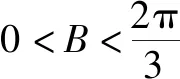
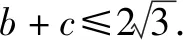
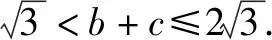
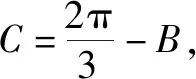
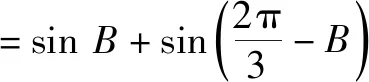
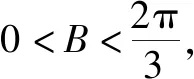
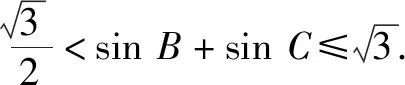
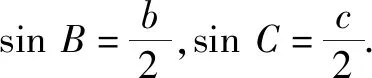

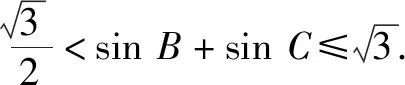
4.3 反思悟道,固化创新思维元素
4.4 目标检测,发展创新思维元素
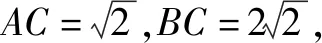
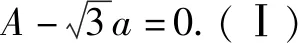


5 教学评价
5.1 设计注重思维培养,促进学生深度学习
5.2 数学情境设置成功,创新思维培养到位
5.3 知识之间跨度较大,思维容量要求较高

