波形钢腹板-UHPC 组合连续箱梁桥静力和抗震性能研究

朱平，丁子贤，张哲，邵旭东

［1.湖南大学土木工程学院，湖南长沙 410082；2.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南长沙 410082；3.湖南工业大学土木工程学院，湖南株洲 412007］

超高性能混凝土（Ultra-high Performance Con⁃crete，UHPC）是一种新型水泥基复合材料，采用颗粒组分优化级配的方式构建，具有非常高的堆积密度［1］，抗压强度可达120～200 MPa［2］.不连续的孔隙结构能有效减少液体的进入，耐久性得到显著提升［3］.掺入的钢纤维在UHPC 基体内不连续且乱向分布，使UHPC 具有持续的开裂后拉伸性能，抗拉强度可超过8 MPa［4］.

目前，大跨径预应力混凝土（Prestressed Con⁃crete，PC）连续梁桥存在自重过大，主跨过度下挠以及梁体开裂严重的难题.造成这些问题的主要原因在于普通混凝土（Normal Concrete，NC）抗拉强度低、徐变系数较大.邵旭东教授研发团队［5］利用UHPC高强度、高耐久性的特征，提出了单向预应力UHPC 薄壁箱梁结构，并将这种新的结构形式应用于工程实践：广东省英德市已建成世界最大跨径的单向预应力UHPC 简支箱梁桥（跨径102 m），该桥运营状态良好，受到工程界的一致好评.

为克服普通混凝土箱梁桥腹板易开裂问题，法国提出由平钢腹板（Flat Steel Web，FSW）代替混凝土腹板的概念.但FSW 沿纵向无法自由伸缩，使得FSWs-NC 组合桥梁预应力损失较严重.为此，法国Campenon Bernar公司提出一种可沿桥梁纵向自由伸缩的新型钢腹板形式：波形钢腹板（Corrugated Steel Web，CSW）［6］.波形钢腹板不约束顶、底板的变形，几乎全部预应力都可作用在顶板和底板上.法国将波形钢腹板引入工程项目中，取得了良好的效果，并在全世界范围推广.法国、德国、日本等国相继建成了Cognac桥、Dole桥、Altwipfergrund桥、日见梦大桥、安威川大桥等，桥型包括简支梁、连续梁、连续刚构、斜拉桥等.我国也建成了江苏淮安长征人行桥［7］、鄄城黄河公路大桥、深圳平铁大桥等［8］.CSWs-NC 组合箱梁桥消除了普通混凝土腹板开裂的风险；对比PC箱梁桥，可降低结构自重约1/5～1/4；无腹板钢筋绑扎立模的过程，施工更为简单方便.

虽然CSW 可降低主梁的重量，但箱梁的顶板和底板采用NC 使得组合桥梁的自重仍然较大，并成为制约CSWs-NC 组合箱梁桥跨径进一步增大的瓶颈.NC 具有较大的徐变，使得大跨预应力混凝土连续梁桥中跨跨中过度下挠的问题仍难以有效解决［9-10］.并且，NC 较低的抗拉强度使得顶、底板仍然易开裂；在使用阶段，受压区普通混凝土的正截面最大压应力限值较低，例如16.2 MPa（C50混凝土）.

受已建成UHPC 桥梁自重轻、性能优异的启发，本文尝试将CSWs-NC 组合箱梁桥的顶、底板替换为UHPC 板，提出CSWs-UHPC 组合连续箱梁结构，以期能大幅减轻上部结构自重，提升CSWs-UHPC 组合连续箱梁桥的跨径，改善主梁跨中过度下挠的问题，消除顶、底板开裂的风险.这种新型组合体系桥梁能突破CSWs-NC 组合箱梁桥的瓶颈，成为大跨径连续梁桥中有较强竞争力的一种结构型式.

为验证CSWs-UHPC 组合结构的可行性，本文设计了一座78 m+130 m+78 m 三跨CSWs-UHPC 组合连续箱梁桥，利用Midas/Civil 建立了整桥有限元模型，对其进行静力分析［11］.在此基础上，为便于CSWs-UHPC 组合连续箱梁桥结构设计，本文对该新型组合桥梁的合理中支点梁高、中跨跨中梁高进行了分析，提出组合梁合理的梁高范围.然后，分析了CSWs-UHPC 组合箱梁桥的动力特性；研究了E2 地震波纵向激励作用下，组合梁端位移、墩底弯矩和剪力以及高阻尼橡胶支座的滞回耗能特性，可为CSWs-UHPC组合箱梁桥的工程应用提供参考.

1 波形钢腹板-UHPC组合箱梁桥方案设计

1.1 纵横断面设计

桥梁上部结构为三跨CSWs-UHPC 组合连续箱梁，跨径布置为78 m+130 m+78 m，立面如图1 所示.主桥分左右双幅，单幅桥采用单箱单室截面，中跨跨中及边跨支点梁高为3.5 m，中墩支点梁高为7.5 m.CSWs-UHPC 箱梁顶板宽10.0 m；UHPC 桥面板采用带有纵肋的矮肋板，UHPC 矮肋板的面板厚8 cm，纵肋高14 cm，纵肋间距设为70 cm.UHPC 桥面板下沿纵向每隔2.4 m 设置一道1.1 m 高的UHPC 横肋，横肋厚度为12 cm，形成正交异性UHPC 矮肋板桥面体系，使组合箱梁顶板的主受力方向由横桥向变为纵桥向.UHPC 横肋可有效减小车轮荷载作用下桥面板的纵向应力［12-13］，并有利于体外预应力束的布置.箱梁节段示意图如图2 所示.UHPC 底板宽8.0 m，底板厚度沿纵向在20～45 cm之间变化；腹板采用Q345波形钢腹板.采用节段预制悬臂拼装法施工，相邻节段顶、底板之间采用环氧树脂胶进行接缝处理，相邻CSW 的连接采用焊接.CSWs-UHPC 箱梁截面布置如图3所示.

图1 CSWs-UHPC组合连续梁桥立面布置图（单位：cm）Fig.1 Elevation layout of corrugated steel webs-UHPC composite continuous box girder bridge（unit：cm）

图2 CSWs-UHPC组合箱梁节段Fig.2 Segmental schematic of corrugated steel webs-UHPC composite box-girder

图3 CSWs-UHPC箱梁截面（单位：cm）Fig.3 Typical cross section of corrugated steel webs-UHPC composite box-girder（unit：cm）

1.2 波形钢腹板设计

本桥采用1600 型波形钢腹板［14］，可在工厂采用模压法加工成长6 400 mm 的安装构件后，再运送至制梁场地进行CSWs-UHPC 组合箱梁预制节段的施工.要求CSW 整节段模压成型，节段内无焊缝［15］.CSWs-UHPC 组合连续梁桥的CSW 厚度变化范围为12～28 mm.

1.3 UHPC顶、底板与波形钢腹板的连接

CSW 与UHPC 顶、底板的连接采用翼缘板+栓钉的连接方式.翼缘板厚18 mm，宽550 mm，栓钉直径22 mm，高100 mm，横向间距为200 mm，纵向间距为150 mm，一个翼缘板上可布置3列栓钉.UHPC 顶、底板连接件的布置形式相同.

1.4 UHPC横隔板

在CSWs-UHPC 组合连续箱梁桥边跨和中跨各设置4道和8道横隔板，以提高主梁抵抗扭转畸变的能力，横隔板厚度为16 cm.部分横隔板兼具体外预应力的转向作用，该类横隔板在靠近底板处为马蹄形，厚50 cm.UHPC 横隔板与波形钢腹板之间采用栓钉连接.

1.5 单向预应力体系

CSWs-UHPC 组合箱梁结构中密集布置的UHPC 横肋与矮肋式UHPC 顶板形成正交异性桥面体系［13］，顶板无须设置横向预应力，仅沿桥梁纵向设置预应力，从而形成单向预应力CSWs-UHPC 组合连续箱梁体系.由于组合箱梁的UHPC 顶板和底板较薄，为合理布设预应力筋，采用全体外预应力形式［16］.体外预应力束采用Φs15.2 高强度低松弛环氧涂覆无黏结成品索［17］，悬臂体外顶板束位于顶板下方，靠近顶板处布置；合拢体外底板束位于底板上方，靠近底板处布置.

1.6 应用前景分析

按照桥梁跨径、桥宽、跨中和支点梁高以及结构设计性能目标相同的原则，设计了CSWs-NC 组合连续箱梁桥和预应力混凝土连续箱梁桥，与本文提出的CSWs-UHPC 组合箱梁桥进行对比.3 种方案均采用节段预制悬臂拼装法施工，CSWs-NC 组合箱梁桥和PC 连续箱梁桥的截面布置分别如图4 和图5所示.

图4 CSWs-NC组合箱梁桥截面布置图（单位：cm）Fig.4 Typical cross section of CSWs-NC composite continuous box girder bridge（unit：cm）

图5 PC连续箱梁桥截面布置图（单位：cm）Fig.5 Typical cross section of PC continuous box girder bridge（unit：cm）

1.6.1 上部结构自重及有效性分析

3 种方案的上部结构自重及自重效应对比如表1 所示.由表1 的数据可以看出，CSWs-NC 组合箱梁桥对比PC箱梁桥，上部结构自重降低了16.6%，中支点负弯矩减小了14.6%，活荷载效应比增加了15.0%，说明仅将混凝土腹板替换为波形钢腹板对于降低中支点负弯矩和提高结构有效性的作用有限.相对于CSWs-NC 组合箱梁桥和PC 箱梁桥，CSWs-UHPC 组合箱梁桥上部结构自重分别降低了45%和54%，自重荷载作用下中支点负弯矩分别降低了45.8%和53.8%，活荷载效应比（活荷载效应与总效应之比）则分别增加了66.9%和91.8%.这表明使用CSWs-UHPC 组合箱梁这种结构型式能显著降低自重，大大减小中支点处负弯矩，结构抵抗活荷载的有效性得到明显增强，对提升连续梁桥主跨跨越能力具有较大潜力.

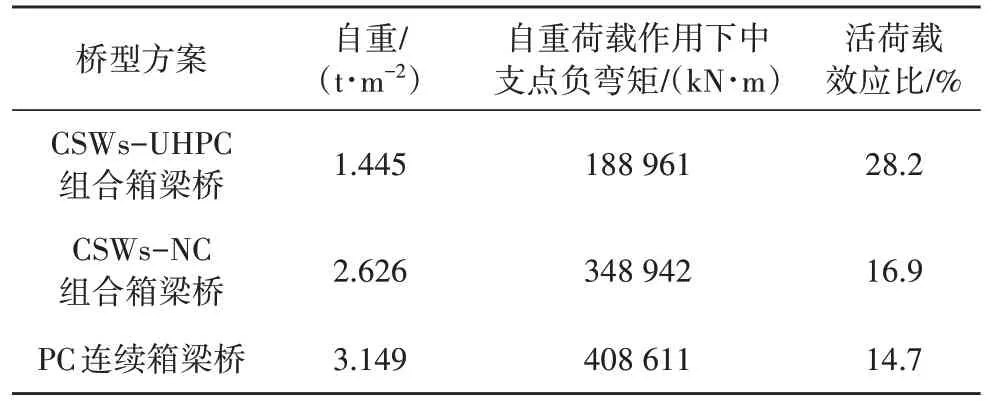
表1 结构自重及有效性对比Tab.1 Comparisons of dead weight and its effectiveness

1.6.2 耐久性和经济性分析

PC 箱梁桥存在较为严重的耐久性病害，如梁体开裂、跨中过度下挠［9，18-19］、体内预应力管道压浆不密实导致的预应力筋锈蚀等问题［17］.CSWs-UHPC 组合箱梁顶、底板采用UHPC 替换NC，使箱梁顶、底板基本无开裂风险；波形钢腹板无开裂隐患，且桥梁钢结构防腐技术也已经相当成熟；预制CSWs-UHPC组合箱梁结构在蒸汽养护后，UHPC 顶、底板的后期收缩可基本消除，并且徐变也远小于NC，可有效解决传统大跨梁桥跨中过度下挠的问题；CSWs-UHPC组合箱梁桥采用全体外预应力体系，体外预应力束采用无黏结钢绞线外包HDPE 防护［17］，易检测，可更换，耐久性优异.

将CSWs-UHPC 组合箱梁桥的经济性与CSWs-NC 组合箱梁桥及PC 箱梁桥进行对比，如表2 所示.CSWs-UHPC 组合箱梁桥上部结构自重大幅降低，使得运输吊装费用降低，下部结构材料用量也可减少.经估算，对比CSWs-NC 组合箱梁桥和PC 连续箱梁桥，CSWs-UHPC 组合箱梁桥的综合单价仅分别增加了16.8%和6.5%.但CSWs-UHPC 组合箱梁桥耐久性能优异，且能避免传统大跨径梁桥各种常见病害的产生，可大幅度降低桥梁病害所带来的后期养护费用，综合而言，CSWs-UHPC 组合箱梁结构在桥梁全寿命周期成本上仍具有竞争力.

表2 方案经济性比选表Tab.2 Economic performance among different bridge types

2 波形钢腹板-UHPC 组合箱梁桥静力性能分析

采用有限元软件Midas/Civil 建立CSWs-UHPC组合连续箱梁桥的空间杆系模型，模型包含84 个梁单元.按照体外预应力钢束的形状并设定适当的摩擦系数，在模型上施加预应力荷载以模拟体外预应力钢束的作用.模型的计算假定：1）波形钢腹板与UHPC 顶和底板固结，并共同受力；2）UHPC 顶板和底板承担纵向弯矩，波形钢腹板承担横向剪力；3）组合梁弯曲时符合平截面假定.

有限元模型中相关参数取值为：1）UHPC 材料性能参考《超高性能混凝土梁式桥技术规程》（T/CCES 27—2021），UHPC 弹性模量取41.9 MPa，泊松比取0.2，抗压、抗拉强度设计值分别取58 MPa、3.3 MPa，抗压强度标准值取84 MPa［22］.CSW 和预应力筋的材料特性参考《波形钢腹板组合梁桥技术标准》（CJJ/T 272—2017）［14］；2）一期恒载按桥梁设计自重取值，二期恒载为32.5 kN/m；考虑整体温升和温降20 ℃，梯度温升、温降按照《公路桥涵设计通用规范》（JTG D60—2015）取值［23］；汽车荷载等级为公路-Ⅰ级；支座沉降取值为：边支座沉降5 mm，中支座沉降10 mm；经高温蒸养后，UHPC 的徐变系数终极值取为0.2［22］.

2.1 承载能力极限状态分析

CSWs-UHPC 组合连续箱梁的最小弯矩、最大弯矩设计值及弯矩抗力如图6所示，由图6可知主梁抗弯承载力计算满足规范《超高性能混凝土梁式桥技术规程》（T/CCES 27—2021）要求［22］.

图6 主梁弯矩包络及抗力图Fig.6 Bending moment envelope and flexural resistance of the main girder

主梁最大剪力、最小剪力及剪力抗力如图7 所示，由图7 可知主梁抗剪承载力计算满足规范CJJ/T 272—2017要求［14］.

图7 主梁剪力包络及抗力图Fig.7 Shear envelope and resistance of the main girder

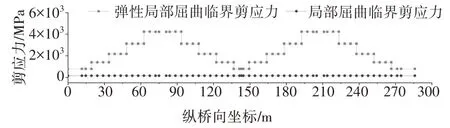
图8 局部屈曲剪应力Fig.8 Local shear buckling stress

图9 整体屈曲剪应力Fig.9 Global shear buckling stress

《波形钢腹板组合梁桥技术标准》（CJJ/T 272—2017）规定CSW 剪应力设计值不应超过组合屈曲临界剪应力［14］，即：

式中：τmd为剪力与预应力的竖向分力产生的剪应力设计值，MPa；τtd为扭矩产生的剪应力设计值，MPa；τcr为波形钢腹板组合屈曲临界剪应力，MPa；τcr，L为波形钢腹板局部屈曲临界剪应力；τcr，G为波形钢腹板整体屈曲临界剪应力.

求得组合屈曲临界剪应力τcr=155 MPa，剪应力设计值τmax=52.3 MPa.可知试设计方案CSW 承载能力极限状态剪切稳定满足规范CJJ/T 272—2017 要求［14］，且具有较大的组合屈曲剪应力富余.

剪力连接件受剪承载力应符合下式要求：

经计算可知，栓钉单位长度水平受剪承载力设计值和水平剪力设计值分别为2 128 N/mm 和1 132 N/mm，栓钉连接件受剪承载力满足规范要求.

2.2 施工及使用阶段应力分析

表3 给出了施工阶段和使用阶段的应力值，从表中可以看出施工阶段应力和正截面压应力均低于规范T/CCES 27—2021 限值［22］，荷载频遇组合作用下无拉应力出现，且具有一定的应力储备.

表3 施工及使用阶段应力Tab.3 Stresses during construction and service stages MPa

2.3 合理梁高范围分析

在上述分析中，CSWs-UHPC 组合箱梁桥的梁高取值参考了已建成的主跨为120～150 m 的CSWs-NC组合箱梁桥方案，目前缺少可直接用于CSWs-UHPC组合连续箱梁桥设计的梁高参数.本节在结构静力分析的基础上，对CSWs-UHPC 组合箱梁桥中支点和中跨跨中的合理梁高范围进行分析，以便对主跨跨径为100～200 m 的CSWs-UHPC 组合连续箱梁桥的结构设计提供可直接参考的合理梁高范围.

2.3.1 中支点和中跨跨中合理梁高范围分析

由组合结构内力和应力分析得到中支点梁高的下限值.随着中支点梁高的降低，中支点负弯矩降低，中跨跨中正弯矩增大.为满足使用阶段抗裂要求，必须增大中跨合拢底板束的数量，可能导致使用阶段正截面最大压应力超过0.5fck=42 MPa［22］.根据计算可得到中支点梁高的下限值为6.0 m，高跨比为1/22.

由挠度计算得到中跨跨中梁高的下限值［22］.分别计算了中支点梁高为6.0 m、6.5 m、7.0 m、7.5 m 时对应的中跨跨中梁高临界值，计算结果见表4.

表4 不同梁高组合下主跨跨中挠度Tab.4 Deflection under different combinations of beam depths

由表4 可知：当组合梁中支点梁高为6.0 m、6.5 m、7.0 m、7.5 m 时，中跨跨中梁高的下限临界值分别为2.5 m、2.4 m、2.3 m、2.2 m.计算得到的中支点梁高与主跨跨径比和跨中梁高与主跨跨径比下限值的关系曲线如图10 所示.从图10 可以看出：中跨跨中梁高跨径比的下限值随支点梁高跨径比的增大而大致呈线性减小的趋势，拟合线性方程为Hm/L=-0.2Hs/L+0.029，即中跨跨中与中支点的梁高比为Hm/Hs=-0.2+0.029L/Hs，Hs表示中支点梁高，L表示中跨跨径，Hm表示由先行确定的中支点梁高推算得到的中跨跨中梁高的下限值.

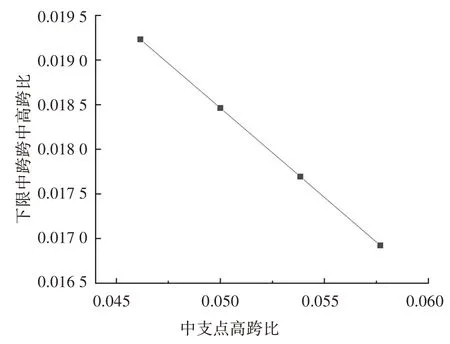
图10 中支点高跨比-中跨跨中高跨比下限值关系图Fig.10 Ratio of girder depth at support to mid span length versus the lower limit of the ratio of girder depth at midspan to mid span length

在初始方案的基础上，增加梁高使中支点附近的波形钢腹板更容易发生整体屈曲，并且增加用钢量.参考PC 连续箱梁桥梁高取值范围的上限值［24］，可得到CSWs-UHPC 组合连续箱梁桥梁高上限值，即中支点梁高与中跨跨径比Hs/L为1/16，中跨跨中梁高与中支点梁高比Hm/Hs为1/1.5.

综上可知，CSWs-UHPC 组合连续箱梁桥合理梁高范围为：中支点梁高与中跨跨径比Hs/L为1/16～1/22，中跨跨中梁高与中支点梁高比Hm/Hs为1/1.5～（-0.2+0.029L/Hs）.

2.3.2 采用梁高限值的组合桥梁方案受力分析

分别采用合理梁高范围的上限值和下限值，进行相应CSWs-UHPC 组合连续箱梁桥的受力分析.方案1 取合理梁高范围的下限值，中支点梁高为6.0 m，中跨跨中梁高为2.5 m；方案2 取合理梁高范围的上限值，中支点梁高为8.1 m，中跨跨中梁高为5.4 m.计算结果如表5所示.

表5 采用梁高临界值的CSWs-UHPC组合结构应力Tab.5 Stresses of the CSWs-UHPC composite plans with critical depths MPa

从表5 可以看出：当分别采用合理梁高范围的上限值和下限值时，CSWs-UHPC 组合箱梁桥的受剪承载力和使用阶段应力均满足规范要求［9，14］.在进行CSWs-UHPC 组合箱梁桥结构设计时，梁高取值可参考本文提出的合理梁高范围.

将2.3.1 节中得到的CSWs-UHPC 组合箱梁桥合理梁高范围与PC 箱梁桥和CSWs-NC 组合箱梁桥的中支点及中跨跨中梁高设计建议值［15，24］进行对比可知：CSWs-UHPC 组合箱梁桥中支点及中跨跨中梁高的下限值小于PC 连续箱梁桥和CSWs-NC 组合箱梁桥.这是因为CSWs-UHPC 组合箱梁桥的自重显著降低，中支点负弯矩和跨中正弯矩大大减小，在合理范围内降低梁高可满足承载力要求.并且本设计方案中所采用的UHPC 的抗压强度标准值是C50 混凝土的2.6 倍，在使用阶段可承受更大的正截面压应力.因此，当跨径和荷载条件相同时，CSWs-UHPC 组合箱梁桥的梁高取值可小于CSWs-NC 组合箱梁桥和PC箱梁桥.

3 动力性能分析

为探究CSWs-UHPC 组合连续箱梁桥的动力特性，分别建立了CSWs-NC 组合箱梁桥、PC 连续箱梁桥以及CSWs-UHPC 组合连续箱梁桥的有限元模型，并考虑了下部结构尺寸变化的影响，对不同桥梁方案的动力特性和在E2 地震作用下的非线性动力时程进行了对比分析.

3.1 模型概况

CSWs-UHPC 组合箱梁桥A、CSWs-NC 组合箱梁桥及PC 箱梁桥采用相同的下部结构方案，布置情况为：1#、4#桥墩高19 m，采用矩形空心截面，边长为8 m×2.6 m，壁厚0.8 m；2#、3#桥墩高15 m，采用边长8 m×5 m 矩形空心截面，壁厚1.0 m，如图11、图12（a）所示.为符合工程实际，CSWs-UHPC 组合连续箱梁桥B采用截面尺寸缩减的主墩.由于CSWs-UHPC组合箱梁桥上部结构自重比PC 箱梁桥降低了54%，所受的汽车制动力与PC 箱梁桥相同，综合考虑，CSWs-UHPC 组合箱梁桥B 的2#、3#桥墩采用边长8 m×4 m 矩形空心截面，壁厚0.8 m，如图12（b）所示，1#、4#墩则与其他三种方案相同.各桥梁方案的桥墩横截面尺寸如表6 所示.建立的有限元模型忽略了桩土的相互作用，各墩底在地面处固结.

图11 桥墩与支座布置图（单位：m）Fig.11 Layout of piers and supports（unit：m）

图12 主墩截面布置（单位：cm）Fig.12 Typical cross section of main pier（unit：cm）

表6 桥墩横截面尺寸Tab.6 Cross section dimension of pier

在1#和4#墩顶设置LNR 矩形滑动型支座；2#和3#墩顶设置HDR（I）型隔震高阻尼橡胶支座.HDR 支座和LNR 支座的滞回模型如图13 所示.2#、3#墩顶的HDR 支座带有剪力键，在正常使用和常遇地震状况下，剪力键起到限制主梁位移的作用；而在罕遇地震下，剪力键可“熔断”，隔震高阻尼橡胶支座通过较大的水平剪切变形能力耗散地震能量［25］.

图13 支座滞回模型Fig.13 Hysteretic model of bearings

3.2 地震波选择

地震荷载工况为：分区特征周期0.4 s，场地类型Ⅱ，设防烈度8（天然地震波峰值加速度为0.3g）［26］.计算得到E2 地震设计加速度反应谱最大值Smax=1.275g.根据设计加速度反应谱E2，采用SIMQKEGR 软件，分别生成E2 人工地震波3 条，地震波峰值加速度为0.51g，持续时间均为40 s，E2 人工地震波如图14 所示.由于横桥向地震作用下桥墩的内力和位移较小，本文仅考虑2#制动墩在纵桥向地震波作用下的内力响应.

图14 E2人工地震波Fig.14 E2 artificial seismic wave

3.3 自振频率与振型

4 种桥梁方案的自振频率与振型特征如表7 所示.由表7 可以看出：对于第1～第5 阶振型，CSWs-UHPC组合箱梁桥A与CSWs-UHPC组合箱梁桥B的自振频率基本相同.4种桥梁方案的第1阶振型均表现为主梁横向弯曲，CSWs-UHPC 组合箱梁桥的自振频率最低，为0.260 Hz；CSWs-NC 组合箱梁桥的自振频率与CSWs-UHPC 组合箱梁桥相差较小，为0.272 Hz；PC 箱梁桥自振频率最高，为0.490 Hz.这是因为CSWs-UHPC 与CSWs-NC 组合箱梁桥采用波形钢腹板，抵抗横向弯曲的能力较弱.

CSWs-UHPC 组合箱梁桥第1、2、4 阶为横向弯曲，第5阶为竖向弯曲；CSWs-NC组合箱梁桥第1、3、5 阶为横向弯曲，第4 阶为竖向弯曲；PC 箱梁桥第1、2阶为横向弯曲，第4、5阶为竖向弯曲，表明3种方案的横向抗弯刚度均弱于竖向抗弯刚度.振型为一阶竖弯时，CSWs-UHPC 组合箱梁桥的频率最大，说明CSWs-UHPC组合箱梁桥的竖向抗弯刚度最大.

3.4 下部结构相同的3种方案地震响应

表8 为下部结构相同的3 种方案在E2 地震波作用下2#桥墩墩底弯矩峰值、剪力峰值以及梁端位移峰值.从表8 中的数据可以看出：CSWs-UHPC 组合箱梁桥的弯矩峰值、剪力峰值以及梁端位移峰值均小于CSWs-NC 组合箱梁桥和PC 箱梁桥；CSWs-UHPC 组合箱梁桥A 的墩底弯矩峰值对比CSWs-NC组合箱梁桥和PC 箱梁桥分别降低了20%和31%；其墩底剪力峰值对比CSWs-NC 组合箱梁桥和PC 箱梁桥则分别降低了22%和29%.这是因为CSWs-UHPC组合箱梁桥上部结构自重相比CSWs-NC 组合箱梁桥和PC 箱梁桥分别降低了45%和54%，使得地震作用下的惯性力大幅降低，因此墩底的弯矩和剪力也显著降低.

从表8 中的数据还可以看出：CSWs-UHPC 组合箱梁桥梁端纵向位移对比CSWs-NC 组合箱梁桥和PC箱梁桥分别降低了25%和23%.CSWs-NC组合箱梁桥与PC 箱梁桥梁端纵向位移峰值仅相差3%，而CSWs-NC 组合箱梁桥的自重比PC 箱梁桥降低了16.6%，原因是PC 箱梁桥一阶纵飘对应的自振频率较大（见表7），地震作用下位移响应降低，从而抵消了由于较大的惯性力而增加的位移响应.

表8 地震响应对比Tab.8 Comparisons of Seismic responses

图15 所示为E2-1 地震波作用下中墩支座的滞回曲线.CSWs-UHPC 组合箱梁桥支座位移、水平力及滞回曲线包围面积小于CSWs-NC 组合箱梁桥和PC箱梁桥，相比CSWs-NC组合箱梁桥和PC箱梁桥，CSWs-UHPC 组合箱梁桥支座滞回曲线包围的面积分别降低了41.3% 和49.0%.在地震波激励下，CSWs-UHPC组合箱梁桥需要耗散的能量大大降低.

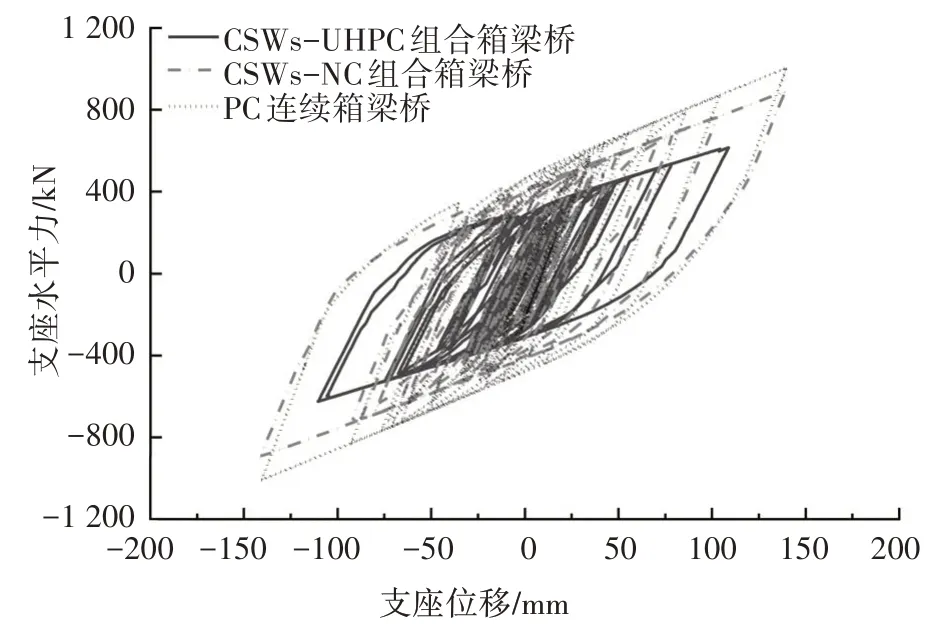
图15 支座滞回曲线Fig.15 Hysteretic curves of bearing

3.5 下部结构不同的组合箱梁桥地震响应

由图16 可以得出：CSWs-UHPC 组合箱梁桥A与CSWs-UHPC 组合箱梁桥B 的支座滞回曲线基本重合.

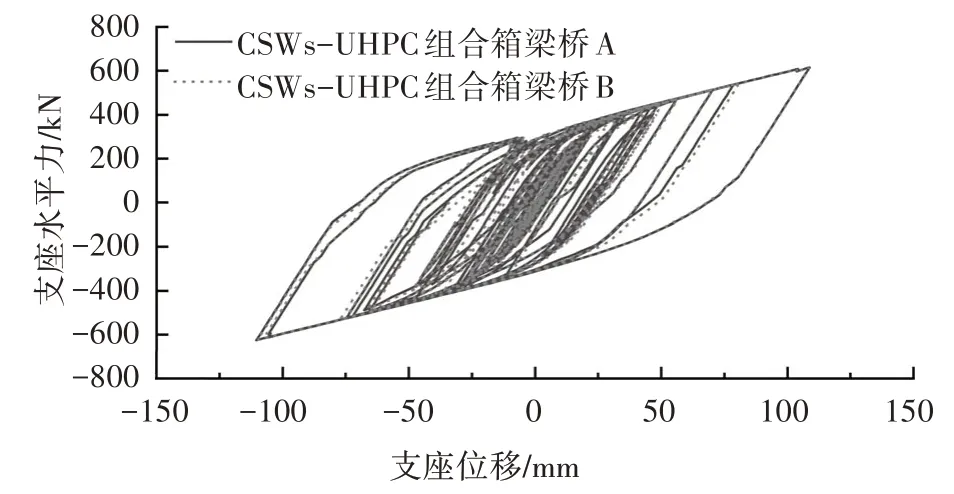
图16 CSWs-UHPC组合箱梁桥支座滞回曲线Fig.16 Hysteretic curves of bearing of CSWs-UHPC composite box girder bridges

当主墩横截面尺寸不同时，表9 给出了CSWs-UHPC 组合箱梁桥在E2 地震波作用下2#桥墩墩底弯矩峰峰值、剪力峰值以及梁端位移峰值.从表9 中的数据可以看出：CSWs-UHPC 组合箱梁桥B 的墩底弯矩和剪力峰值对比CSWs-UHPC 组合箱梁桥A 分别降低了10%和14%.由于CSWs-UHPC 组合箱梁桥A、B 主墩的支座滞回曲线基本重合，即2#、3#桥墩墩顶所受的支座水平力基本相同.2#、3#桥墩截面尺寸减小后，桥墩的纵桥向弯曲刚度和重量降低，在地震荷载及支座水平力的作用下，墩底弯矩和剪力降低.但CSWs-UHPC 组合箱梁桥A 与CSWs-UHPC 组合箱梁桥B的梁端位移峰值基本相同.

表9 CSWs-UHPC组合箱梁桥地震响应对比Tab.9 Comparisons of Seismic responses of CSWs-UHPC composite box girder bridges

由以上分析可以得出：在E2 地震波作用下，CSWs-UHPC 组合箱梁桥可降低梁端位移以及中墩墩底处的弯矩和剪力，使得隔震橡胶支座所需要消耗的能量显著降低.CSWs-NC 组合箱梁桥和PC 箱梁桥在地震荷载作用下的纵向位移较大，需要设置一定数量的阻尼器以减小纵向位移；而CSWs-UHPC组合箱梁桥可不设阻尼器或仅设置较少数量的阻尼器即可满足结构抗震的需求.

4 结论

本文利用UHPC 的高强度、高韧性的特点，设计了一座大跨径全体外预应力CSWs-UHPC 组合连续箱梁桥，对其进行了结构静力和抗震性能分析，并将其与CSWs-NC 组合箱梁桥及PC 连续箱梁桥进行对比，得到如下结论：

1）对比CSWs-NC 组合箱梁桥和PC 箱梁桥，CSWs-UHPC 组合箱梁桥的自重分别降低了45%和54%，CSWs-UHPC 组合箱梁桥的使用荷载作用效应占总效应的比例分别提高了66.9%和91.8%，对提升连续梁桥主跨跨越能力具有较大潜力.

2）CSWs-UHPC 组合箱梁桥上部结构自重的大大降低，能进一步减少下部结构的工程量，降低运输吊装成本，且UHPC 在桥梁运营期不需要养护，CSWs-UHPC 组合箱梁桥全寿命周期成本具有一定的优势.

3）130 m 跨径波形钢腹板-UHPC 组合箱梁桥合理梁高范围为：中支点高跨比Hs/L=1/16～1/22，中跨跨中梁高与中支点梁高比Hm/Hs=1/1.5～（-0.2+0.029L/Hs）.

4）由于CSWs-UHPC 组合箱梁桥上部结构自重较轻，惯性荷载大大降低，地震响应显著降低；CSWs-UHPC 组合箱梁桥可不设阻尼器或仅设置较少数量的阻尼器即可满足结构抗震的需求.

综上所述，CSWs-UHPC 组合箱梁桥具有良好的全寿命周期经济性和静力性能，其自重、结构有效性和抗震性能对比CSWs-NC 组合箱梁桥和PC 箱梁桥均具有明显优势，是大跨径连续梁桥中一种有较强竞争力的结构型式.