磁路互补型横向磁通切换直线电机电磁推力计算与特性分析
付东山 吴康伊 郑 萍 王祥瑞 伍小杰
磁路互补型横向磁通切换直线电机电磁推力计算与特性分析
付东山1吴康伊1郑 萍2王祥瑞1伍小杰1
(1. 中国矿业大学电气工程学院 徐州 221116 2. 哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001)
有铁心永磁直线电机由于齿槽、边端效应及电枢电流谐波等,不可避免地会产生较高的电磁推力波动,电磁推力波动直接影响直线电机运行精度和平稳性。该文对具有磁路互补特征的横向磁通切换直线电机展开电磁推力特性研究,通过等效磁路法分析其磁场分布规律,得出该电机次级具有等磁位的电磁特性;基于气隙磁动势-磁导分析方法,揭示互补磁路条件下,该有铁心电机消除齿槽推力波动,实现有铁心电机无齿槽效果的机理;基于该电机磁场分布特征,建立其许-克变换气隙磁场计算模型,提出定位力、电枢绕组磁阻力及永磁推力等电磁推力快速准确的计算方法,获得该电机各电磁推力特性;对样机进行了空载感应电动势和电磁推力的测试实验,对比实验和仿真结果,验证了理论分析模型及计算方法的有效性和准确性。
直线电机 横向磁通 磁通切换 磁路互补 电磁推力 许-克变换
0 引言
永磁直线电机(Permanent Magnet Linear Motor, PMLM)具有高速度、高精密、大行程和高动态特性等优点,在各类高精密工业伺服场合有重要应用价值[1]。但有铁心永磁直线电机齿槽效应、端部效应以及电枢电流谐波等引起的推力波动会随着电机输出的电磁推力无缓冲地施加到负载上,影响高精密直线伺服精细平滑运动,干扰其平稳运行。
永磁直线电机本体在推力波动抑制方面主要包括电机结构型式调整、结构参数的优化设计、新型拓扑等。
在电机结构型式调整方面,主要通过极槽配合、初/次级分段、斜极或错位、磁极调整、额外辅助齿等方式减小电机定位力和抑制推力波动。文献[2]提出非整数极的三段式初级结构,通过非整数极提高电枢绕组电动势正弦性、减小电枢绕组电流谐波产生的推力波动,通过分段式结构实现各段结构定位力相互制约达到削弱总定位力;文献[3]采用初、次级分段和V型磁极错位结构削弱端部磁阻力产生的推力波动;文献[4]针对Halbach交替极永磁直线电机采用双边错齿结构,不断抑制齿槽力,也提高绕组正弦度;文献[5]采用磁极错位的结构削弱法向齿槽力谐波;文献[6]采用初级铁心错位结构和极槽配合的方法消减端部力和抑制推力波动;文献[7]采用端部添加辅助齿结构降低气隙磁场谐波和改善绕组电感不对称,实现推力波动的降低。
上述通过结构型式调整抑制推力波动的方法有一定效果,但改变电机结构时,常常忽略其他结构参数及其耦合的变化对推力波动带来的影响,同时结构的改变会增加电机的体积或增加电机的加工 难度。
在电机结构参数的优化设计方面,通过结构参数的优化,降低电机推力波动。文献[8]采用磁极结构参数优化气隙磁场,降低推力波动;文献[9]基于代理模型的优化算法,采用加点准则等方式实现全局优化设计,最终实现推力波动降低的同时提高推力密度;文献[10]通过Kriging模型辅助的多目标粒子群优化,对敏感参数进行提取,实现推力优化设计;文献[11]针对推力波动不同分量产生原因,分别采用边端齿结构参数优化和绕组匝数电感优化实现抑制边端力和改善绕组电感不对称效果。
上述结构参数优化设计,通过寻找全局最优等方法,可得到最优结构参数,实现推力密度和推力波动的相对最优解,然而由于拓扑结构的约束,其优化范围有限,推力波动的抑制程度有限。
为了提升直线电机性能,不断有新型直线电机拓扑提出,其中部分拓扑结构具有削减定位力的优势。文献[12]提出平板型磁通切换横向磁通永磁直线电机结构,对比磁通切换电机发现该结构具有低定位力的特点,但该文同时指出该结构存在漏磁严重、推力偏低的问题;文献[13]提出永磁体磁路并联互补的初级永磁横向磁通直线电机,通过使用分段错开的次级铁心,使每个永磁体的磁路呈并联且互补,从而减少了推力波动,该电机两个绕组分别对应永磁体不同磁路,绕组交替与永磁体作用,绕组利用率不高,此外每个永磁体均需单独占用一个初级励磁齿,降低了电机推力密度;文献[14]基于文献[13],将永磁体置于初级槽口实现偏置励磁,将直流励磁线圈缠绕在初级励磁齿上,提出混合励磁横向磁通直线电机,该电机依然保持互补磁路结构,具有低定位力,但增加了额外励磁线圈,占用电枢绕组绕制空间,同时带载能力较弱。
上述采用电机本体结构的改变和优化的方法,在推力波动减小方面具有一定效果,但上述文献对直线电机推力特征研究较少,文献[15]采用能量法,通过对磁共能来求取电磁推力。文献[16]采用安培定律法,通过等效永磁体在电枢磁场运行产生安培力进而求取电磁推力。上述推力的求取方法简单便捷,但只初步求取了电枢绕组和永磁体间相互作用的推力,精度不高,没有求取电机定位力和电枢绕组磁阻力。如何快速准确求取电机定位力、电枢绕组电流产生的磁阻力、永磁体和电枢绕组间相互作用力等电磁推力,是直线电机分析推力、减小推力波动的一个关键问题。
针对上述问题,本文在文献[17]前期研究工作的基础上,对斜气隙圆筒型横向磁通切换永磁直线电机进行磁场分布与电磁推力特性分析。首先,通过磁场分布分析发现,永磁体励磁时次级铁心处磁位均保持不变。因此电机次级铁心既可以采用文献[17]提出的硅钢片叠压制成,也可将整个或部分次级采用导磁碳钢制成,从而降低制造成本,提高次级的机械强度,解决圆筒型直线电机次级过长、固定困难的问题。其次,进行气隙磁场调制分析,证明通过合理选取次级极距和次级齿厚度,可实现该电机永磁体磁通回路互补,具有可以极大地削减定位力、消除齿槽效应的特点。然后,针对该电机三维磁路结构,采用有限元计算耗时、磁路法求解复杂的问题,本文提出该电机基于许-克变换(Schwarz- Christoffel transformation)的气隙磁场快速计算模型,建立定位力、电枢绕组磁阻力、永磁推力快速计算的方法,并对推力特征进行分析。最后,对实验样机进行了空载感应电动势和各电磁推力的测试实验,通过对比仿真和实验结果,验证了基于许-克变换快速推力计算方法的有效性和准确性。
1 电机磁场分布规律
1.1 电机结构与运行原理
图1给出本文研究的斜气隙圆筒型磁通切换横向磁通永磁直线电机(Oblique Air-gap Tubular Transverse Flux Switching Permanent Magnet Linear Motor, OATTFS-PMLM)的拓扑结构。初级单元沿着运动方向依次排列形成初级结构,每个初级单元包含若干个初级铁心和永磁体,永磁体和两边相邻的初级铁心齿共同形成初级磁极,绕组缠绕在初级磁极上。相同凸极次级铁心沿着运行方向镜像翻转交替排列并固定在次级固定轴上组成次级结构。
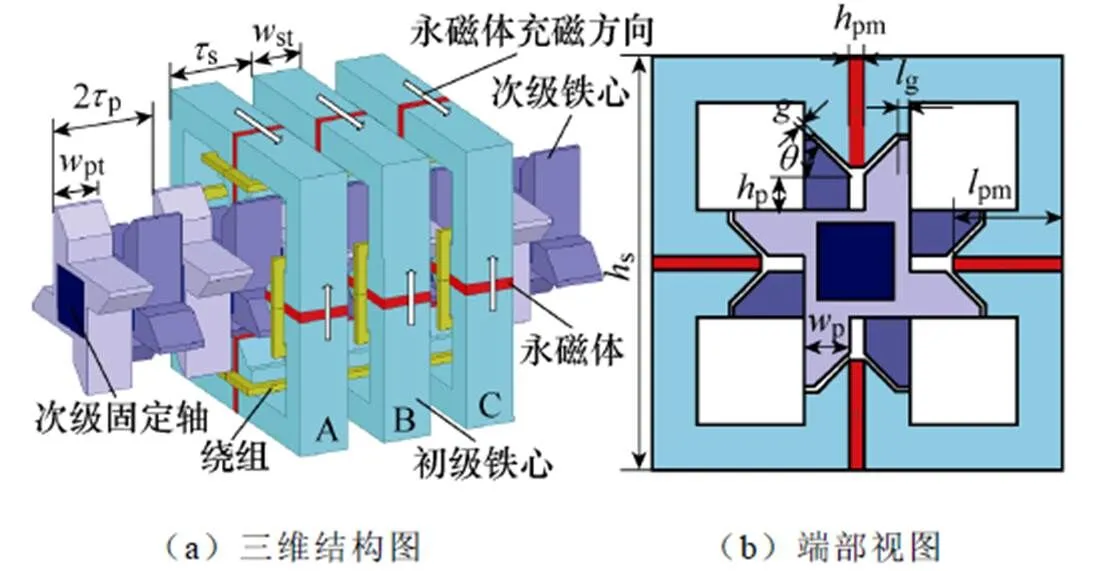
图1 OATTFS-PMLM结构
永磁体励磁磁通回路如图2a和图2b所示,从图2中可以看出,初级单元与不同次级铁心对齐时,永磁体在电枢绕组中产生的磁链方向相反,当初级动子移动时通过初级绕组的磁链就会发生变化而产生交变感应电动势,当初级绕组中通入交变电流时,电枢磁场与永磁体磁场相互作用,推动动子向前移动。由于该电机具有横向磁通电机的结构特点,易于实现多极结构,因此在相同供电频率下,能够达到更低的速度,并具有较高的力密度,适用于低速大推力直接驱动场合。
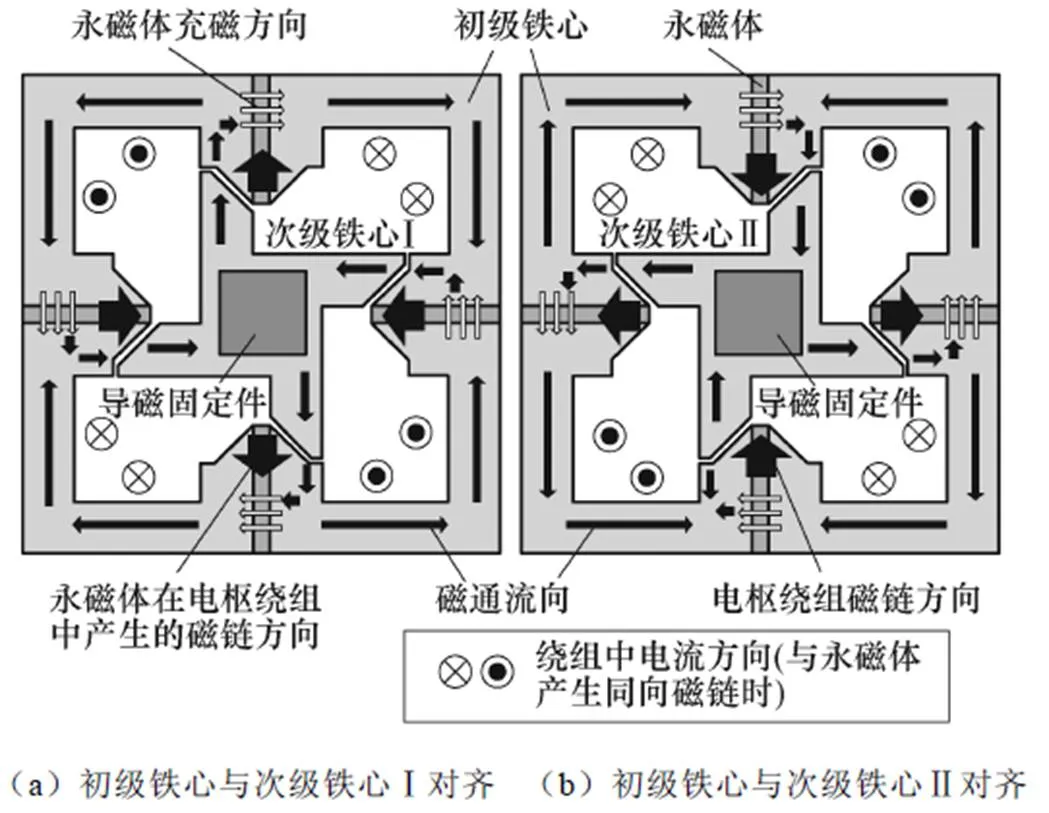
图2 OATTFS-PMLM的磁路
1.2 磁场分布
等磁位线如图3所示。图3中,电流源或永磁体等磁源对称分布时,磁源产生的磁位矢势方向垂直于对称中间线。此时,单位强度的磁极从无穷远处沿着中间线移动至中间线上任意位置,为反抗磁场而做的功始终为零,因此图中的中间线为等磁位线且与无穷远处磁位相同。

图3 等磁位线
基于此建立电机等效磁网络模型,为了分析简单,在建立磁网络模型时忽略铁心磁阻,所建立的磁网络模型包括气隙磁导、永磁体内磁导、漏磁导、永磁体磁动势。在只有永磁体激励、初级单元与不同次级单元对齐时的磁场分布情况如图4所示[17],图中pm、、、、、分别为永磁体内磁导、初级单元齿与次级铁心Ⅰ齿间的气隙磁导、初级单元与次级铁心Ⅰ间不与绕组相交链的磁回路而形成的漏磁导、初级单元与次级铁心Ⅱ齿间的气隙磁导、初级单元与次级铁心Ⅱ间不与绕组相交链的磁回路而形成漏磁导、不经过次级铁心的等效漏磁导。
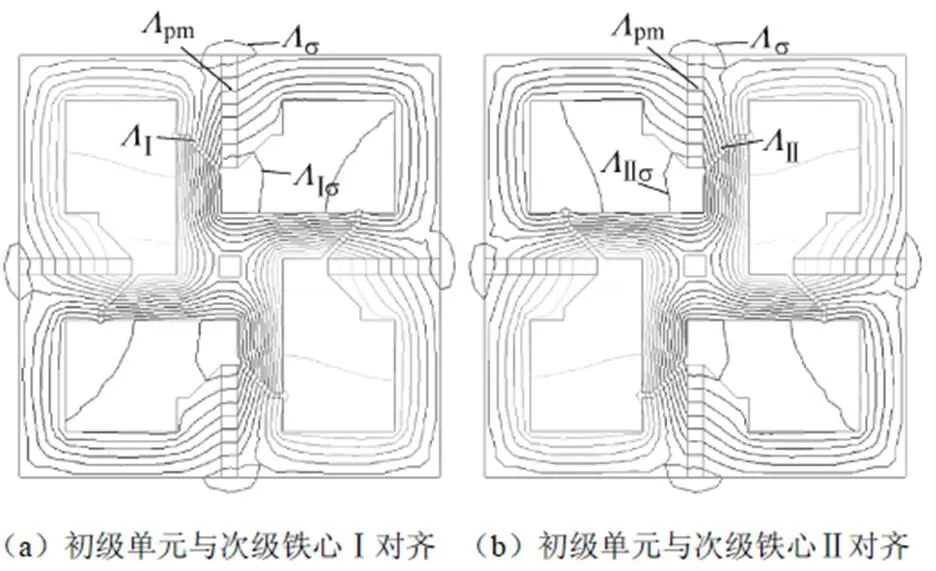
图4 OATTFS-PMLM永磁体激励下的磁路情况
将每个永磁体沿中间线分开为两部分,每部分等效为磁势源和磁导串联。电机的磁网络模型如图5所示,初级单元分别与次级铁心Ⅰ和Ⅱ对齐时的磁网络模型如图5a和图5b所示。电机在运行时,初级单元与不同次级铁心对齐并有一个交替的过程,需要考虑电机运行过程中初级单元与不同次级铁心交替作用的情况,将图5a、图5b所示磁网络模型合并为如图5c所示的电机磁网络模型。由于电机结构的对称性,各个齿的相关参数相同,图中只标注一个齿的参数。
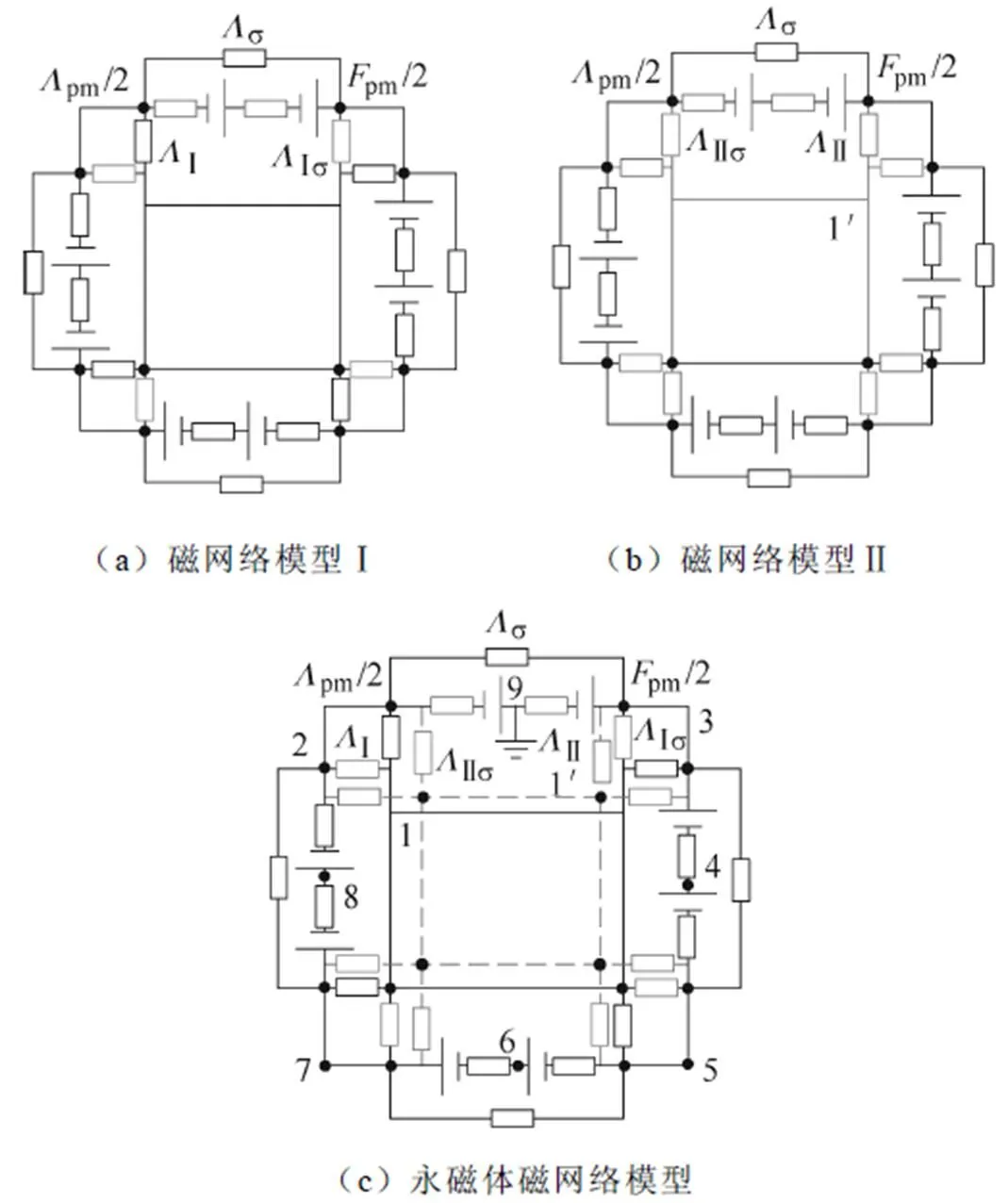
图5 OATTFS-PMLM永磁体激励下的磁网络模型
对电机磁网络模型采用节点电压法分别计算不同节点的磁位情况,其中参考磁位点设为图5c中节点9,该参考点位于永磁体中间线上,其磁位与无穷远处磁位相同。相关节点磁位为
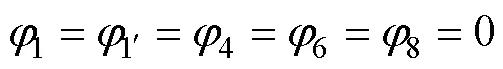
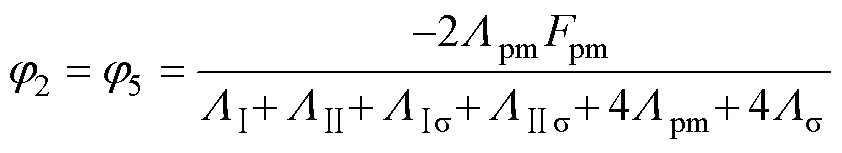
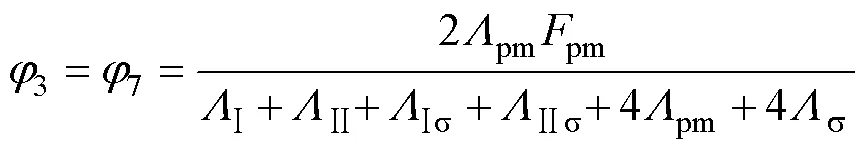
从式(1)可知,该电机无论初、次级相对位置如何变化,次级磁位均保持不变并和无穷远处磁位相同。
因此,次级铁心Ⅰ和次级铁心Ⅱ之间没有磁位差,不存在次级铁心间因磁位差相互影响而导致漏磁的现象。因此可以根据对机械强度等的需要,将次级铁心和次级固定轴分别采用硅钢叠片和导磁碳钢制成,也可以将次级整体采用导磁碳钢制成,而不影响电机的磁路分布,降低制造成本,提高次级的机械强度,解决圆筒型直线电机次级过长,固定困难的问题。
图1中次级铁心齿的极距p和铁心齿纵向厚度pt可以相等,即p=pt,此时,永磁磁通回路通过次级铁心形成互补磁路,即成为磁路互补型横向磁通切换直线电机,该电机在运行过程中初、次级铁心齿间重合面积始终保持不变,消除齿槽引起的定位力,实现有铁心电机无齿槽的效果。
2 基于气隙磁动势-磁导的定位力分析
前面基于OATTFS-PMLM运行原理,分析了该电机的磁场分布规律,得到电机不同位置的磁位分布情况,具有磁路互补特点,消除了齿槽引起的定位力。本节将运用气隙磁动势-磁导对该电机定位力进行分析,从数学模型上阐明在磁路互补情况下定位力的消除机理。
2.1 OATTFS-PMLM气隙等效磁导与磁动势
OATTFS-PMLM电机的三维视图如图1所示,初、次级均可等效为凸极结构,因此初级永磁磁动势受到次级凸极齿的调制作用,产生相应的气隙磁通密度谐波。次级铁心Ⅰ和次级铁心Ⅱ磁位相同,互不干扰,次级铁心Ⅰ和次级铁心Ⅱ中磁通经过的气隙是相互分开独立的。因此,基于次级铁心与初级分别作用的不同气隙,将次级磁导模型分为两个不同部分。
该电机次级不同铁心凸极结构对应不同气隙磁导模型如图6所示。
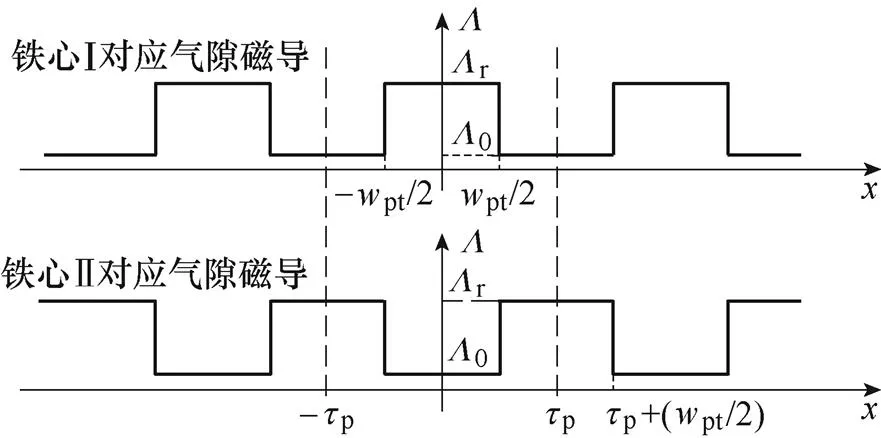
图6 OATTFS-PMLM次级气隙磁导模型
OATTFS-PMLM永磁体磁动势模型如图7所示。图中,st为初级单元厚度,p为永磁体在气隙的等效磁动势。永磁体产生的磁动势在不同气隙中,其方向不同,该电机初级单元间相互独立,可分析单个初级单元,然后根据电机初级单元个数和初级单元间相位差进行叠加。
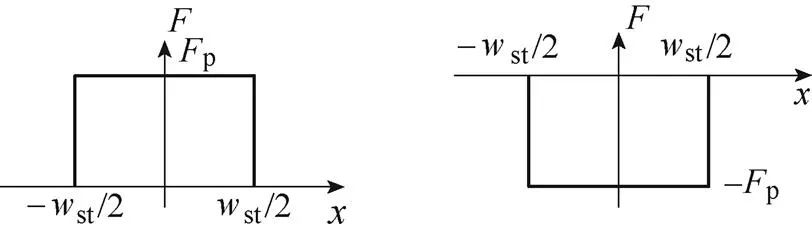
图7 OATTFS-PMLM永磁体磁动势模型
2.2 OATTFS-PMLM定位力机理分析
OATTFS-PMLM定位力是电机绕组不通电时位于初级永磁体和次级铁心凸极齿相互作用产生的。从磁场能量变化的角度出发,可将定位力理解为:由于次级铁心凸极齿的存在,气隙磁导呈周期性分布,初、次级相对运动引起气隙磁场储能变化,进而产生定位力。下面基于能量法对定位力进行推导。
电机气隙中存储的磁场能量为
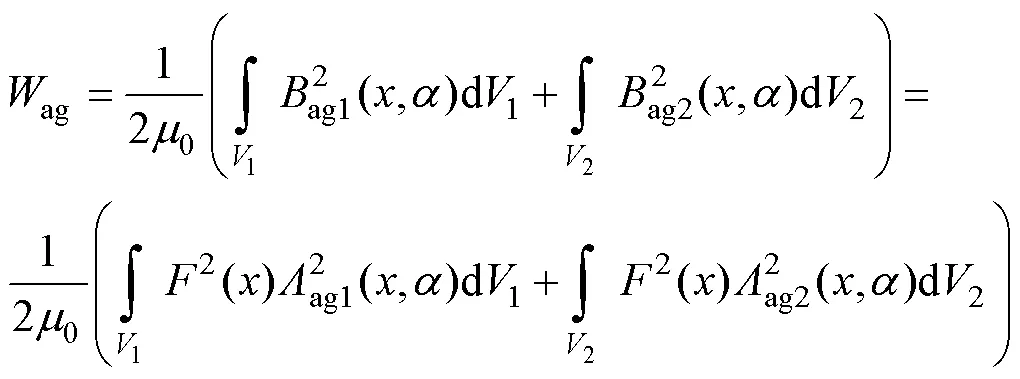
式中,1、2分别为次级铁心Ⅰ和次级铁心Ⅱ对应的气隙体积;为初级与次级之间的相对位置,=0设定为初级与次级铁心Ⅰ对齐的位置;0为气隙磁导率;()、ag1(,)、ag2(,)分别为气隙磁动势分布、不同次级铁心Ⅰ和次级铁心Ⅱ对应的气隙磁通密度的分布;ag1(,)、ag2(,)分别为对应气隙的次级磁导模型。
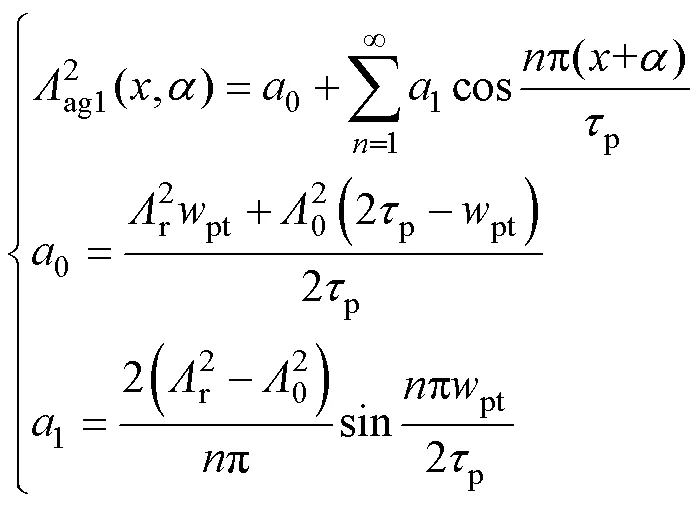
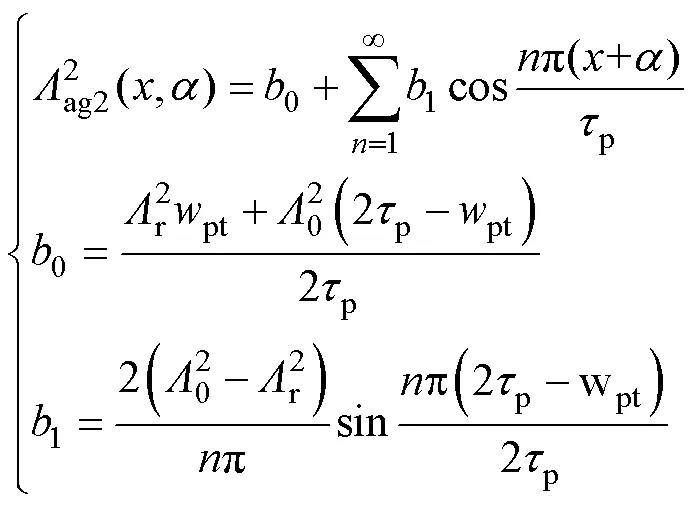
单个初级单元永磁体产生的气隙磁动势模型如图7所示,由于该磁动势模型为一个方波,在不同气隙中,磁动势呈相反方向,幅值相同。因此在不同气隙中,磁动势二次方根相同。
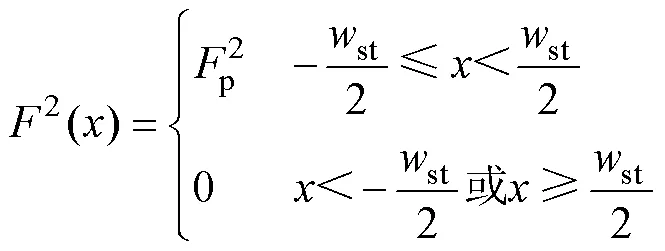
电机的定位力可表示为
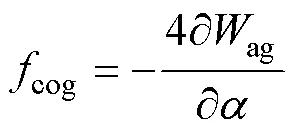
将式(4)~式(7)代入式(8),可得
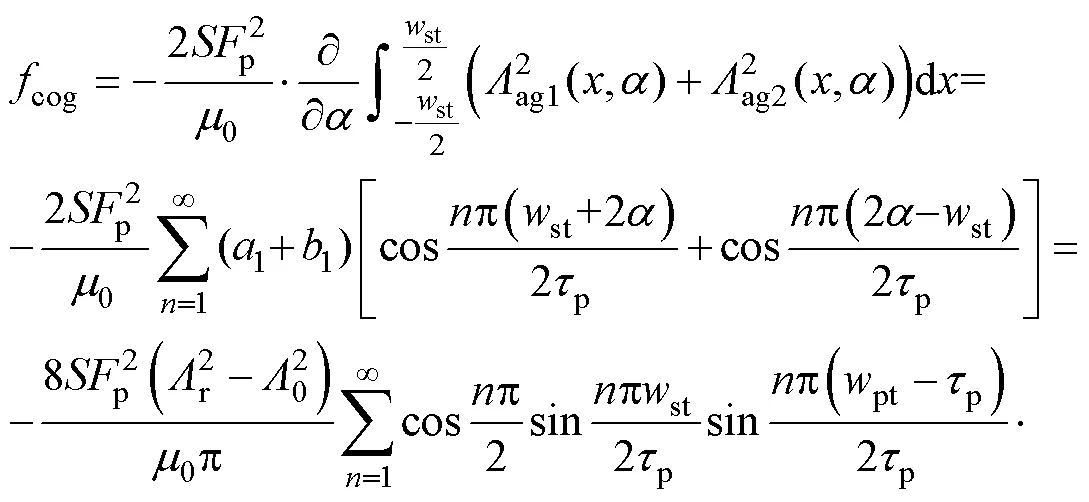
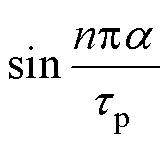
由于电机次级铁心同磁位,相互间没有影响,次级铁心齿厚度pt取值范围为[0,p],由式(9)可知,铁心齿厚度pt接近次级铁心间距p时,定位力逐渐减小;当pt与p相等时,定位力为零。另外,该电机初级单元间相互独立,初级单元厚度选取灵活,从式(9)可以看出,当初级单元厚度st=p时,电机定位力为零。
由上述理论分析可以看出,OATTFS-PMLM综合了横向磁通和磁通切换结构的优势,实现初、次级结构相互独立,通过合理选取初级厚度st或次级铁心齿厚度pt,可以形成磁路互补结构进而达到消除电机无齿槽效应、削减定位力,实现有铁心电机无齿槽力的效果。
3 基于许-克变换的电机电磁计算
基于前述对OATTFS-PMLM磁场分布规律以及定位力的理论分析,得出该电机具有次级等磁位,各次级铁心间磁场相互独立,可形成互补磁路结构,消除齿槽效应等优点。但由于永磁体位于初级铁心之间,其在气隙处的磁动势随气隙磁导的变化而变化,为进一步精确快速计算电机内部磁场,得到电磁推力计算式,采用许-克变换方法建立该电机电磁场计算模型,获得电机气隙磁导。
3.1 电机气隙磁场许-克变换分析模型
许-克变换分析是基于边界的磁场分析方法,通过已知的简单磁场来研究待定的复杂磁场[18]。采用许-克变换进行磁场分析时,需找出一个简单且分布已知的磁场,然后建立待确定场与已知场之间的对应关系,再把已知磁场的分布通过对应关系映射到确定场上,从而得到待确定场分布情况。已知磁场的分布区域通常是半平面、条状、矩形等,待确定场分布区域通常是多边形。许-克变换是一种特殊的保形映射,能够将半平面、条状、矩形等映射为一个多边形。映射关系()、-1()可以通过Matlab SC Toolbox采用数值积分的方式求出[19]。为了简化计算,分别对电机不同气隙进行求解建模。将电机分别对应两个不同求解气隙,并将其中一个等效求解气隙模型等效为二维结构,如图8所示。


图8 OATTFS-PMLM气隙等效模型
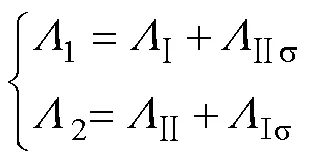
为了采用许-克变换分析方法计算电机初、次级不同相对位置时的气隙磁导,首先将电机初、次级不同相对位置时气隙等效模型进行许-克变换和许-克逆变换,使-Plane气隙等效模型映射为-Plane的矩形,从而计算出初级齿上单位激励下气隙磁场分布情况,进而得到气隙等效模型的气隙磁导,如图9所示。
图9 w-Plane映射到z-Plane的许-克变换
Fig.9 SC mapping between different domains in SC method
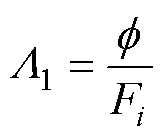
通过许-克逆变换,得到等效气隙域中电流源映射到矩形区域域中的位置,计算单位电流映射到矩形中产生的磁场分布。基于矩形中的磁场分布,通过许-克变换求得电机气隙磁场的磁感应强度的分布情况进而求取相关磁通等参数。
3.2 气隙磁导计算
在域中电流I在 (,) 处产生的矢量磁动 势[19]为
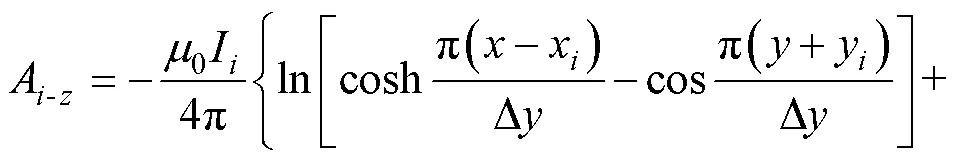
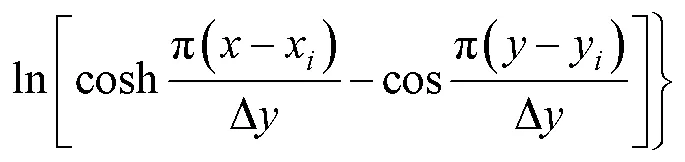
式中,D为矩形的高;(,) 为电流在域中的坐标。
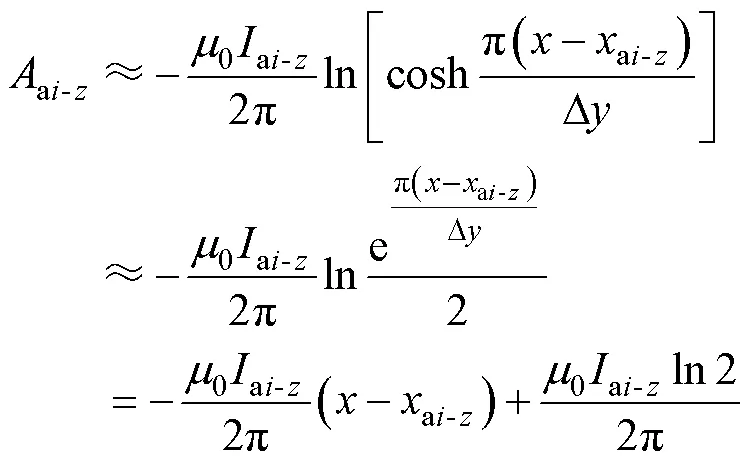
由叠加定理可得,域中线电流和ai产生的矢量磁动势为
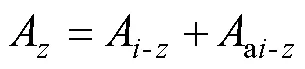
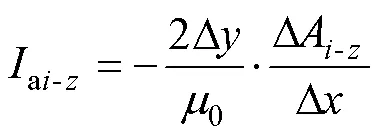
由式(12)~式(15)知在域中的磁感应强度为
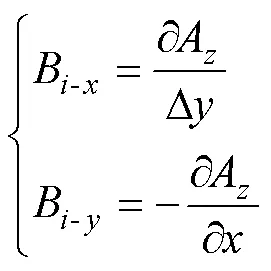
平面中的磁感应强度可以通过下式计算。
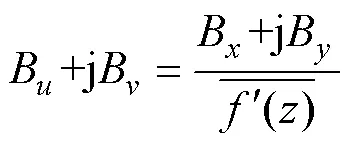
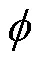
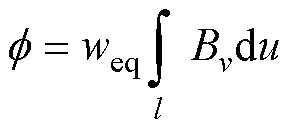
式中,eq为气隙磁场等效厚度。将式(18)代入式(11)中便可得到初、次级不同相对位置下气隙磁导。
3.3 基于气隙磁导的电磁特性计算
为了计算电机电磁特性,将电机永磁体激励等效为直流励磁绕组,永磁体的磁动势pm可以等效为
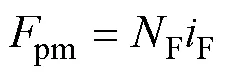
式中,F为等效励磁绕组匝数;F为等效励磁电流。
因此,将电机内部电磁可以等效为永磁体的等效励磁绕组、电枢绕组相互作用产生,通有固定电流的永磁体等效励磁绕组F在电枢绕组A中产生的电动势,即为空载反电动势,可表示为
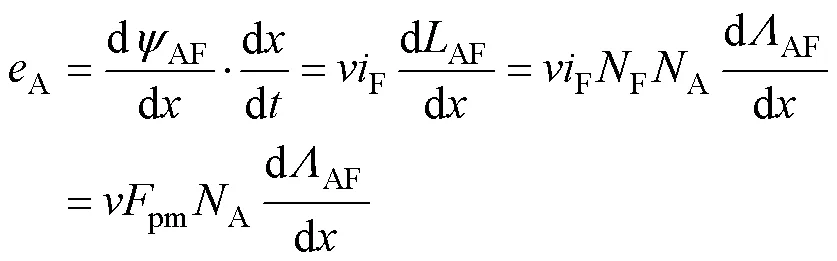
式中,FA为励磁绕组和电枢绕组的互感;AF为互感磁导;A为电枢绕组的匝数;为电机的动子位置;为电机动子运行速度。
电机的输出力是在等效励磁绕组和电枢绕组共同作用下产生的,其值为
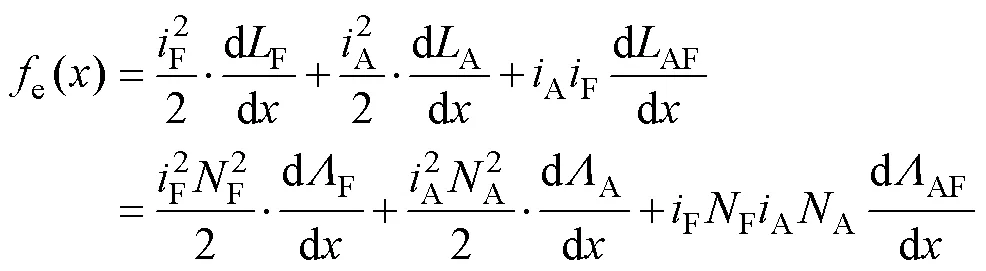
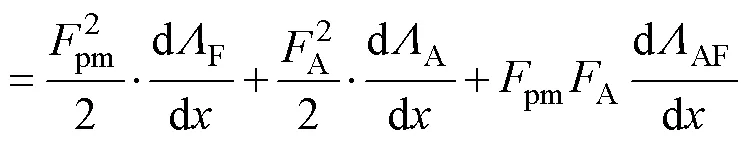
式中,A为电枢电流;A为电枢绕组的磁动势;F为等效励磁绕组的自感磁导;A为电枢绕组的自感磁导。
式(20)、式(21)表明,在激励一定的条件下,电机反电动势以及电机输出推力主要与电机相应绕组的自感磁导以及各绕组间互感磁导决定。考虑电机对称性及电机动子单元极数,等效励磁绕组的自感磁导F、电枢绕组的自感磁导A、互感磁导AF分别可由图5及式(1)~式(3)和式(10)得到。

基于许-克变换分析了OATTFS-PMLM的磁场模型,得到快速分析计算电机气隙磁导的方法。基于气隙磁导,推导出电机定位力、绕组磁阻力和永磁等电磁推力计算模型。
3.4 电磁推力特性分析
从式(21)可知,该电机推力可分解为三部分,式中,第一项为永磁磁动势与永磁等效绕组的自感磁导相互作用产生的电磁推力,此项为电枢绕组为零时电机永磁体产生的磁阻力,即为永磁体作用下电机定位力;第二项为电枢绕组电流产生的电枢磁阻力,该力与电机的电枢电流方向无关,始终指向电枢线圈电感最大的位置;第三项为电枢绕组和永磁体相互作用产生的电磁推力,该电磁推力的大小和方向与电枢绕组电流方向、永磁体充磁方向均有关,该力称为洛伦兹力[20]。将电机的推力分解为定位力、绕组磁阻力和永磁推力,使该电机电磁特性计算模型直接、清晰地表达了不同推力与电机结构之间的关系,为分析电机提供了理论指导。
为了分析该电机各电磁推力特性,考虑电机初级结构相互独立,采用单个初级结构进行分析。电机主要结构参数[17]见表1,相关参数标注如图1所示。永磁体产生的定位力、电枢绕组中通入5A直流电时电枢绕组产生的电枢磁阻力、电枢绕组中通入5A直流电时与永磁体相互作用产生的洛伦兹力,以及上述三项电磁推力的合力(电磁推力)如图10所示。从图10中可以看出,定位力、电枢磁阻力在一个输出周期内呈周期变化,并且周期相同,该电机的定位力、电枢磁阻力主要产生推力波动。
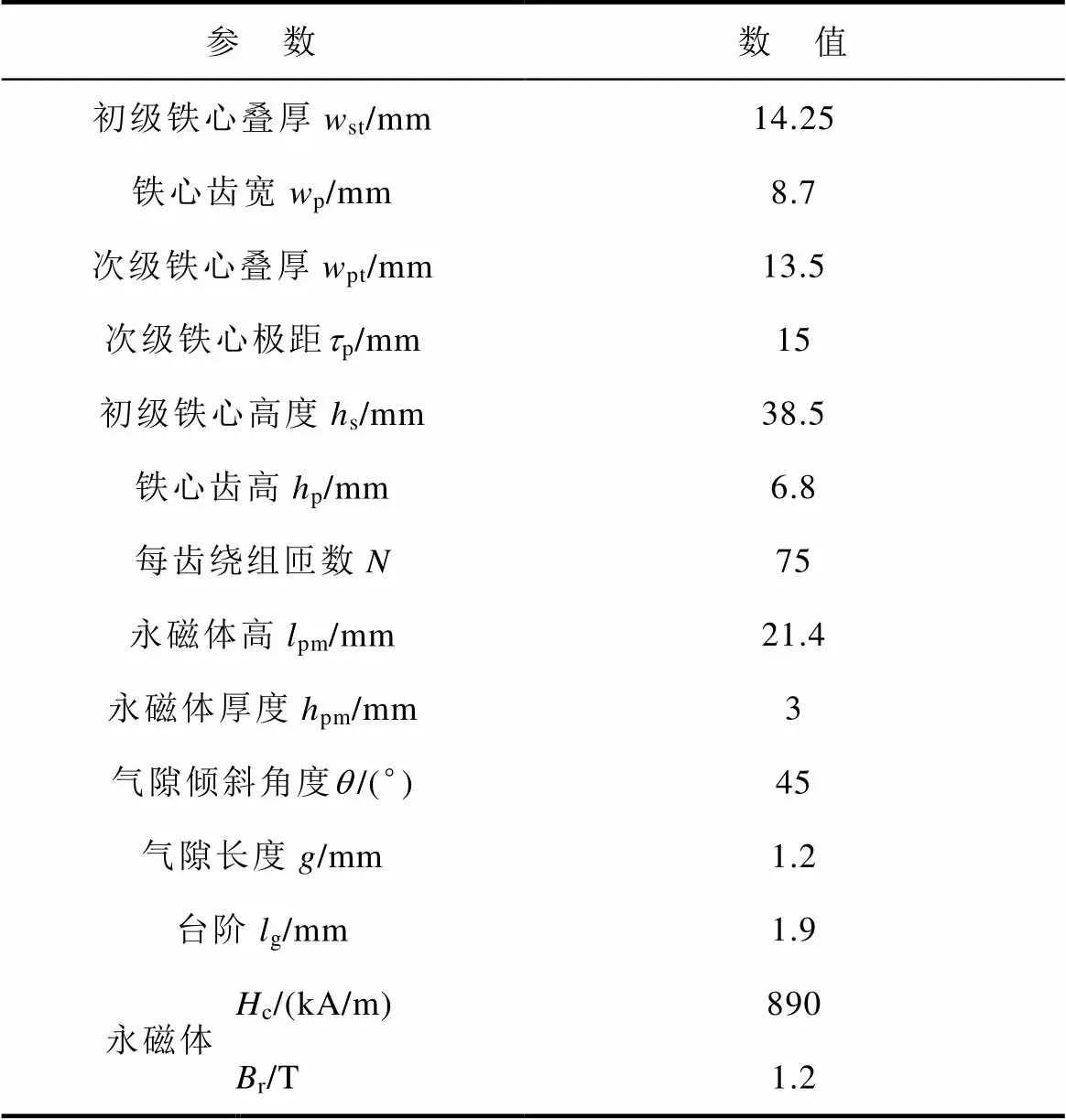
表1 OATTFS-PMLM主要结构参数
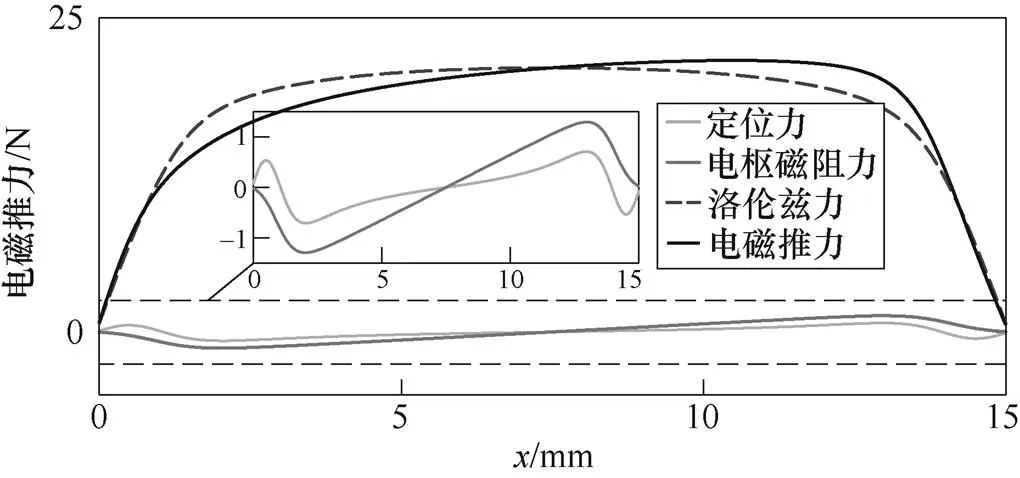
图10 OATTFS-PMLM的电磁推力
4 实验验证
4.1 样机结构
为验证上述理论分析、电磁计算模型的正确性和准确性,搭建样机实验平台进行样机实验,采用有限元仿真计算和实验测试的方法进行验证分析。电机三维有限元模型如图11所示[17]。有限元模型和实验样机主要参数见表1,相关参数标注如图1所示,初级铁心极距s为25mm,每相初级单元数为2。本文实验样机见文献[17]。
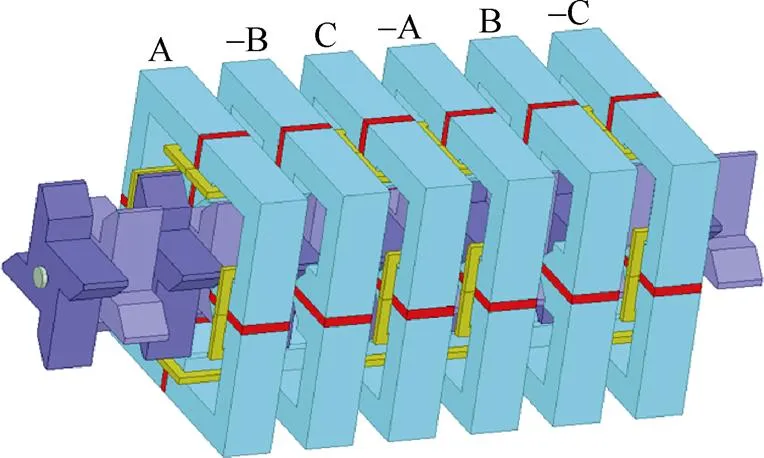
图11 3D有限元分析模型
样机各基本结构如图12所示,初、次级均采用铁心叠片制成,分别如图12a所示,初级铁心和次级铁心均采用相同的铁心结构,次级铁心单元沿着运动方向镜像排列。铁心叠片结构较为简单,加工制作简单。
电机动子装配如图12b所示,采用非导磁框架固定电机初级铁心和永磁体,绕组缠绕在动子磁极上,初级模块进行塑封处理后与次级铁心进行组装,形成图12c所示的样机结构。

图12 样机的结构及装配
4.2 实验测试
图13为搭建的OATTFS-PMLM样机实验平台。滚珠丝杆上的滑块通过力传感器与电机动子连接,力传感器信号通过仪表放大器与示波器连接。

图13 OATTFS-PMLM样机实验平台
电机电枢绕组开路,推动电机动子以1m/s的速度匀速直线运动,测得三相电枢的反电动势波形如图14所示,同时给出相同条件下许-克变换模型和有限元计算的反电动势波形。许-克变换、有限元、实验测试得反电动势峰值分别为7.7V、7.8V、7.3V,波形较为吻合。存在偏差的原因为实际铁心磁导率以及模型等效的理想化处理等。图14表明OATTFS- PMLM许-克变换模型计算电磁场的有效性,并验证了电机原理的正确性。
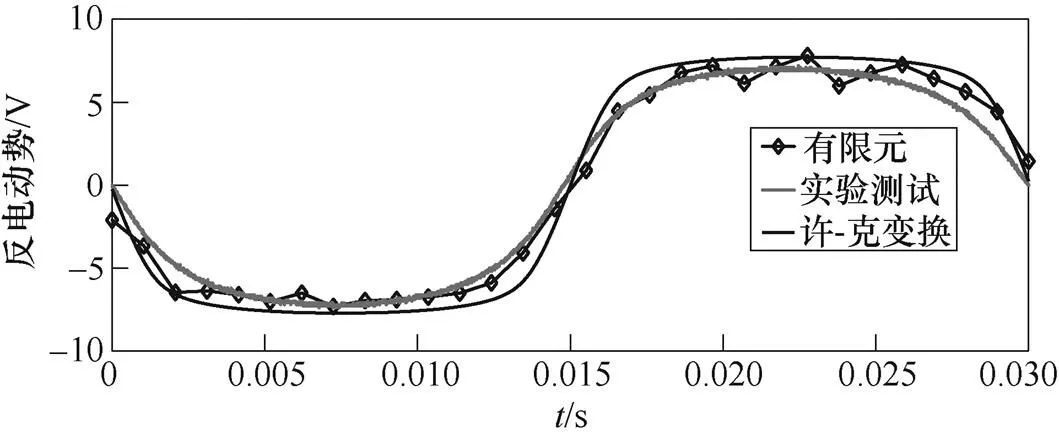
图14 OATTFS-PMLM的电枢绕组开路时反电动势波形
通过滚珠丝杠旋转,丝杠滑块连接力传感器缓慢匀速推动电机初级做直线运动,由于动子匀速运动且速度低,因此可以认为初级在一个极下的任意位置均处于准平衡状态。此时保持电机电枢绕组开路,通过力传感器测得电机波动的定位力和轨道固定的滑动摩擦力,提取其中定位力并与有限元和许-克变换模型计算值进行比较。相关定位力波形如图15所示,在实验测得的定位力消除了特定谐波分量,主要是因为定位力幅值低于导轨的摩擦力,测量误差干扰较大。误差不仅是由于导轨摩擦产生的噪声干扰,还与测试精度有关。许-克变换模型将气隙分开考虑,简化了计算,与有限元相比节省计算时间,在分析定位力时具有一定参考意义。
在推动电机动子做匀速直线运动,单独给电机的一相通入5A的直流电,得到电机静态推力。静态推力曲线如图16所示,实验测得电机最大静推力为42.8N,有限元计算所得最大静推力为42.9N,许-克变换模型计算最大静推力为44.1N,由图16可见,实验曲线与三维电磁场有限元计算以及模型计算的结果基本吻合,表明了模型计算的准确性。
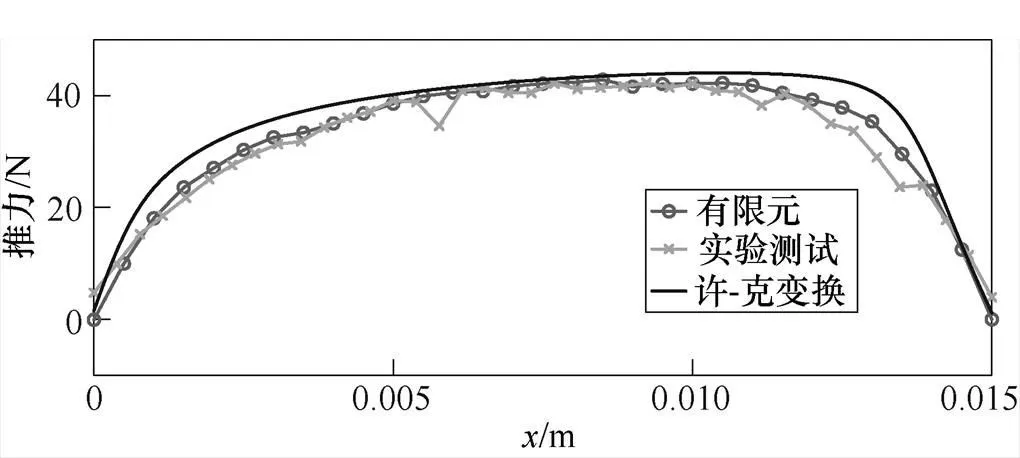
图16 静态推力曲线
采用d=0的控制方法,施加有效值为5A的电枢电流,驱动电机运行,三维有限元和许-克变换模型得到电机输出推力情况如图17所示,许-克变换模型计算电机输出推力平均值为105N,三维有限元计算的推力平均值为99.5N,导致误差的原因主要为许-克变换模型将铁心导磁理想化,同时简化电机模型。两者计算所得电机推力波形吻合度较高。推力波动实验表明许-克变换模型具有较高的准确性。
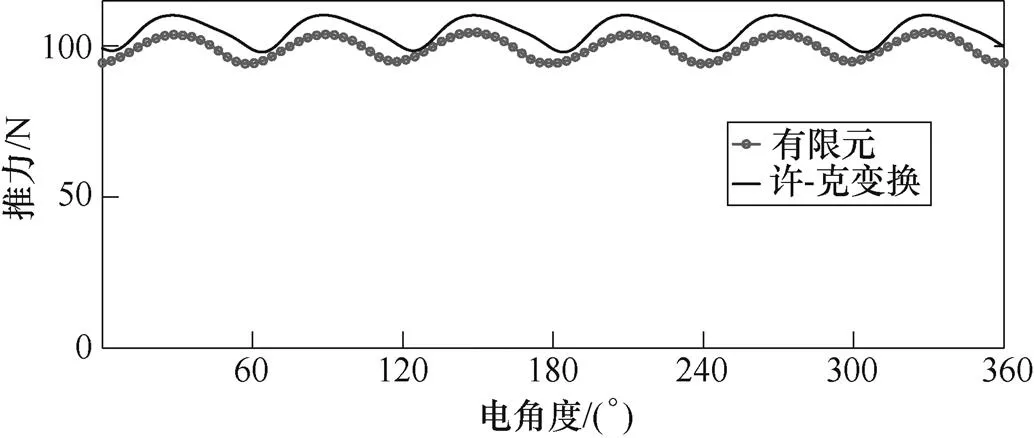
图17 OATTFS-PMLM的推力波形
5 结论
本文针对一种新型斜气隙圆筒型横向磁通切换直线电机进行了电磁推力特性分析,介绍了该新型直线电机的基本结构和运行原理,并对其磁场分布特性定位力进行分析,建立了电机的基于许-克变换的快速求解电磁分析模型并对推力特性进行分析,利用有限元和样机实验对该分析模型的有效性进行了验证并分析了电机的基本特性,得出如下结论:
1)该电机结构中,次级结构磁位不随初级和次级相对位置变化而变化,始终保持不变并等于无穷远处磁位,因此可以将次级作为一个整体采用导磁碳钢制成,而不影响电机的磁路分布,降低制造成本,提高次级的机械强度,解决圆筒型直线电机次级过长时,固定困难的问题。
2)采用气隙磁导-磁动势进行定位力分析,揭示该结构电机具有消除齿槽引起的定位力的优势,可实现有铁心电机无齿槽的效果。
3)建立该电机基于许-克变换的气隙磁导计算模型,实现电机气隙磁导快速精确计算,分别确立电机的定位力、电枢绕组磁阻力、永磁推力快速计算方法,为分析电机电磁推力特性,进一步优化电磁推力,提供理论指导。
4)进行样机实验,验证了计算模型及分析电机电磁推力特性的正确性和准确性。
[1] 王立俊, 赵吉文, 董菲, 等. 基于自适应内模观测器的永磁同步直线电机高带宽强鲁棒预测电流控制策略研究[J]. 中国电机工程学报, 2019, 39(10): 3098-3106.
Wang Lijun, Zhao Jiwen, Dong Fei, et al. High- bandwidth and strong robust predictive current control strategy research for permanent-magnet synchronous linear motor based on adaptive internal model observer[J]. Proceedings of the CSEE, 2019, 39(10): 3098-3106.
[2] Tan Qiang, Wang Mingyi, Li Liyi, et al. Research on noninteger pole number for segmental permanent magnet linear synchronous motor[J]. IEEE Transa- ctions on Industrial Electronics, 2021, 68(5): 4120- 4130.
[3] 兰志勇, 谢斌, 祝涤非, 等. 基于Ⅴ型三段磁极错位削弱永磁直线电机推力波动的方法[J]. 电工技术学报, 2021, 36(16): 3474-3482.
Lan Zhiyong, Xie Bin, Zhu Difei, et al. Method for weakening thrust fluctuation of permanent magnet linear motor based on Ⅴ-shaped three-stage magnetic pole misalignment[J]. Transactions of China Elec- trotechnical Society, 2021, 36(16): 3474-3482.
[4] 许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833.
Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al. Characteristic of a novel permanent magnet linear synchronous motor with Halbach array consequent- pole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[5] 夏加宽, 沈丽, 彭兵, 等. 磁极错位削弱永磁直线伺服电动机齿槽法向力波动方法[J]. 电工技术学报, 2015, 30(24): 11-16, 37.
Xia Jiakuan, Shen Li, Peng Bing, et al. The magnet-staggered method to weaken the cogging effect normal force ripple of permanent magnet linear servo motor[J]. Transactions of China Electro- technical Society, 2015, 30(24): 11-16, 37.
[6] Huang Xuzhen, Yu Hanchuan, Zhou Bo, et al. Detent-force minimization of double-sided permanent magnet linear synchronous motor by shifting one of the primary components[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 180-191.
[7] Zhao Jing, Mou Quansong, Guo Keyu, et al. Reduction of the detent force in a flux-switching permanent magnet linear motor[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1695-1705.
[8] Chi Song, Yan Jianhu, Shan Liang, et al. Detent force minimizing for moving-magnet-type linear synchronous motor[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-5.
[9] 张邦富, 程明, 王飒飒, 等. 基于改进型代理模型优化算法的磁通切换永磁直线电机优化设计[J]. 电工技术学报, 2020, 35(5): 1013-1021.
Zhang Bangfu, Cheng Ming, Wang Sasa, et al. Optimal design of flux-switching permanent magnet linear machine based on improved surrogate-based optimization algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1013-1021.
[10] 李雄松, 崔鹤松, 胡纯福, 等. 平板型永磁直线同步电机推力特性的优化设计[J]. 电工技术学报, 2021, 36(5): 916-923.
Li Xiongsong, Cui Hesong, Hu Chunfu, et al. Optimal design of thrust characteristics of flat-type permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 916-923.
[11] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883-892.
[12] Zhang Zongsheng, Tang Xu, Zhang Chao, et al. Comparative study on modular longitudinal and transverse flux-switching permanent magnet linear motor[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 33-42.
[13] Zhao Xing, Niu Shuangxia. Development of a novel transverse flux tubular linear machine with parallel and complementary PM magnetic circuit for precision industrial processing[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4945-4955.
[14] Li Zhenghao, Zhao Xing, Niu Shuangxia, et al. Analysis and design of a new relieving-DC-saturation transverse-flux tubular motor with complementary magnetic circuit[J]. IEEE Transactions on Magnetics, 2021, 57(6): 1-5.
[15] 寇宝泉, 杨国龙, 李鹏, 等. 双向交链横向磁通圆筒型直线永磁同步电机的基础研究[J]. 中国电机工程学报, 2012, 32(36): 61-67, 13.
Kou Baoquan, Yang Guolong, Li Peng, et al. Basic research on bidirectional crosslinking transverse flux tubular linear permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2012, 32(36): 61-67, 13.
[16] 寇宝泉, 杨国龙, 周维正, 等. 双向交链横向磁通平板型永磁直线同步电机[J]. 中国电机工程学报, 2012, 32(33): 75-81, 178.
Kou Baoquan, Yang Guolong, Zhou Weizheng, et al. Bidirectional crosslinking transverse flux flat type permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2012, 32(33): 75-81, 178.
[17] 付东山, 贾泽宇, 吴富强, 等. 新型斜气隙圆筒型横向磁通切换直线电机及其建模分析[J]. 中国电机工程学报, 2022, 42(15): 5706-5719.
Fu Dongshan, Jia Zeyu, Wu Fuqiang, et al. Novel oblique air-gap tubular transverse flux switching permanent magnet linear motors and its modeling analysis[J]. Proceedings of the CSEE, 2022, 42(15): 5706-5719.
[18] 崔鹏, 张锟, 李杰. 基于许-克变换的悬浮电磁铁力与转矩解析计算[J]. 中国电机工程学报, 2010, 30(24): 129-134.
Cui Peng, Zhang Kun, Li Jie. Calculation of electro- magnetic force and torque of suspension electro- magnet based on Schwarz-Christoffel transform[J]. Proceedings of the CSEE, 2010, 30(24): 129-134.
[19] Zeng Lizhan, Chen Xuedong, Li Xiaoqing, et al. A thrust force analysis method for permanent magnet linear motor using Schwarz-Christoffel mapping and considering slotting effect, end effect, and magnet shape[J]. IEEE Transactions on Magnetics, 2015, 51(9): 1-9.
[20] 吴红星. 开关磁阻电机系统理论与控制技术[M]. 北京: 中国电力出版社, 2010.
Analysis of Electromagnetic Thrust Characteristics of Magnetic Circuit Complementary Transverse Flux Switching Linear Motor
11211
(1. School of Electrical Engineering China University of Mining and Technology Xuzhou 221116 China 2. School of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China)
Owing to cogging effect, end effect and armature current harmonic, the high electromagnetic thrust ripple is inevitable in permanent magnet linear motor with an iron core, which directly influences the accuracy and smoothness of a linear machine in operating. This paper studies the electromagnetic thrust characteristics based on a flux-switching transverse flux permanent magnet linear motor with a complementary magnetic circuit. Firstly, the magnetic field distribution is analyzed by the equivalent magnetic road method, and the electromagnetic characteristics of the equal magnetic potential in the secondary of the motor are verified. Secondly, based on the air-gap magnetomotive force-permeability analysis method, the cogging thrust is suppressed under the complementary magnetic circuit condition, which realizes the non-cogging effect in the permanent magnet linear motor with the iron core. Then, the Schwarz-Christoffel transform model is proposed to analyze the electromagnetic thrust characteristics based on the air-gap magnetic felid distribution, and an analytical expression of electromagnetic thrust is derived. At last, experiments about no load-induced electromotive force and electromagnetic thrust are carried out to verify the proposed theoretical analysis model.
Linear motor, transverse flux, flux switching, complementary magnetic circuit, electromagnetic thrust, Schwarz-Christoffel transform
TM359.4
10.19595/j.cnki.1000-6753.tces.220840
国家自然科学基金国家重大项目课题(51991385)和江苏省研究生科技与实践创新计划(SJCX22_1173)资助。
2022-05-16
2022-07-24
付东山 男,1990年生,博士,讲师,研究方向为电机系统及其控制。
E-mail: fuds@cumt.edu.cn
伍小杰 男,1966年生,教授,博士生导师,研究方向为电力电子与电力传动。
E-mail: xjwu@cumt.edu.cn(通信作者)
(编辑 郭丽军)

