双绕组永磁同步电机滑模变结构控制

于艳君 崔明恺 柴 凤

双绕组永磁同步电机滑模变结构控制

于艳君 崔明恺 柴 凤

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

双绕组永磁同步电机通过绕组串、并联重构能有效提升系统的运行范围。然而绕组不同模式下的参数变化造成传统PI控制器无法满足系统高品质运行要求。该文针对此类电机的运行特点，研究了一种集转速环控制和抗扰观测的复合滑模变结构控制器，有效抑制了电机参数变化及绕组重构引起的转速动态波动问题。首先，分析了双绕组永磁同步电机不同模式下的工作机理、绕组重构时转速波动产生的原因。其次，设计了滑模变结构控制器以实现控制参数的自适应，快速满足重构瞬间电流关系以抑制动态波动。最后，利用小型原理样机，对采用PI控制器和滑模变结构控制器方案进行了典型工况下的对比实验，验证了所提控制策略的有效性和可行性。

永磁同步电机 双绕组结构 绕组重构 滑模变结构控制

0 引言

车辆电传动系统通常采用电机加变速箱方案实现低速大转矩、宽速域运行以满足车辆需求，但该方案存在换档时间长、体积大等弊端。双绕组永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）利用电子开关使绕组低速串联、高速并联兼顾车辆全工况行驶需求，具有宽高效区、宽速域的独特优势，是车辆电传动系统的重要选择[1-3]。然而该类电机电气参数随绕组串、并联模式不同变化较大，并且绕组串、并联重构过程可能出现较大的转速波动，造成系统动态性能变差，影响车辆运行的平稳性。现有文献主要集中在绕组重构拓扑方面，针对上述问题鲜有研究[2-4]。因此，采用先进控制理论，保证该类电机的高品质动态性能至关重要。

传统PI控制器具有结构简单、易于实现等优点，广泛应用于电机控制领域；但其存在参数自适应能力差等问题[5]。为了解决PI控制器存在的问题，Bang-Bang控制、模糊控制、神经网络控制、预测控制、滑模控制等现代控制理论被应用到高性能电机系统[6-11]。其中，滑模控制对系统参数和扰动不敏感、动态响应速度快、鲁棒性强[12]。利用滑模控制能使转速在有限时间内达到给定值，具有更快的收敛速度和跟踪精度[13]；并且利用滑模抗扰观测器前馈补偿能有效提升转矩波动时的动态响应能力，显著缩短负载突变时的恢复时间[14-15]。对于滑模控制中常见的抖振现象，通过优化控制律可有效解 决[16-18]。基于等速控制律，文献[16]设计了滑模增益随系统状态变化的改进型控制律，文献[17]设计了滑模增益随系统状态改变的指数控制律，文献[18]通过状态变量的一阶导数设计控制律。

绕组重构方面，采用电子开关在极短时间内可完成绕组状态重构。开关方式有三相断流切换、三相直接切换、逐相过零切换等[19-21]。断流切换在重构时使电机电流降至0，存在转矩中断过程；三相直接切换若无法瞬时满足重构前后的电流关系，可能会造成重构瞬间的电流尖峰；逐相过零切换能保证电机有一定的转矩输出，但重构过程中绕组处于非对称状态造成转矩波动并且重构过程延长。

通过上述分析，对于该类电机一方面要解决绕组串、并联模式参数不同带来的控制问题；另一方面要迅速满足重构前后的绕组电流关系。为此，本文提出并设计了基于滑模变结构控制的双绕组电机控制策略。首先分析了双绕组PMSM的工作机理及传统PI控制器存在的问题；其次设计了集转速控制器和抗扰观测器的复合滑模变结构控制器；分析了该控制器在绕组重构前后瞬间的电流输出关系是否满足绕组重构要求；最后在小型原理样机实验平台上进行了对比实验，实验结果验证了该方法能够有效提升该类电机典型工况下的动态性能。

1 双绕组PMSM系统的工作机理

双绕组永磁同步电机定子中具有两套相同的对称三相对称绕组，对应绕组同相位排布，如图1所示，两套绕组的匝数和参数完全相同。

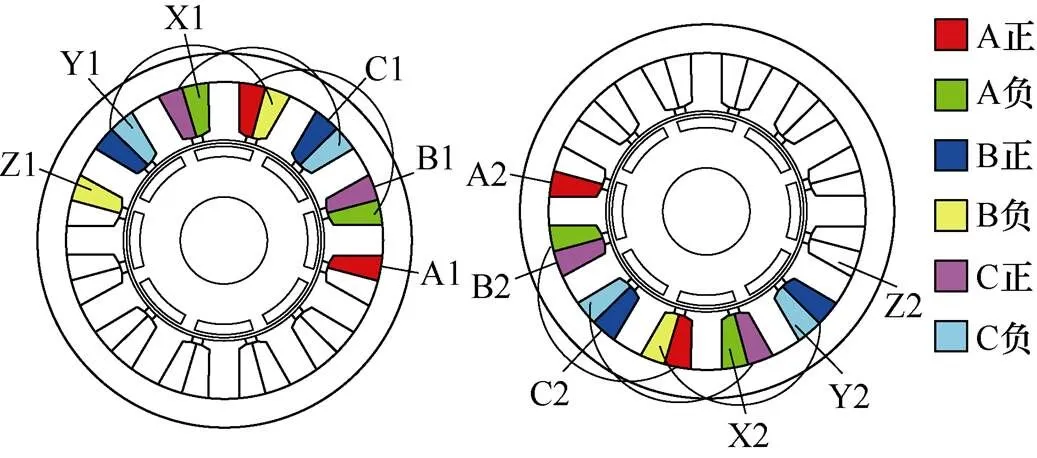
图1 双绕组PMSM的绕组排布

将绕组接入重构开关，控制重构开关的开关状态可实现绕组串、并联状态的切换。图2分别为双绕组永磁同步电机系统绕组串联模式和并联模式的拓扑，S1～S3、P1～P6为绕组重构开关。当S1～S3闭合、P1～P6断开时，两套绕组运行在串联模式；当S1～S3断开、P1～P6闭合时，两套绕组运行在并联模式。

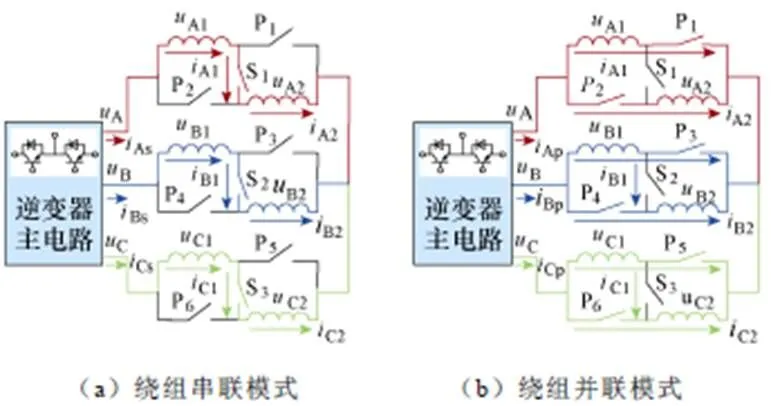
图2 双绕组PMSM系统的拓扑结构

一方面，由图2可得不同工作模式下逆变器侧与电机侧各套绕组电压、电流关系见表1。

由表1电压、电流关系可知：在逆变器容量一定的情况下，低速时采用绕组串联模式，能尽可能地利用逆变器的电流输出极限，提升转矩输出能力；高速时采用绕组并联模式，能充分利用逆变器的电压输出极限，拓宽电机的调速范围，如图3所示。

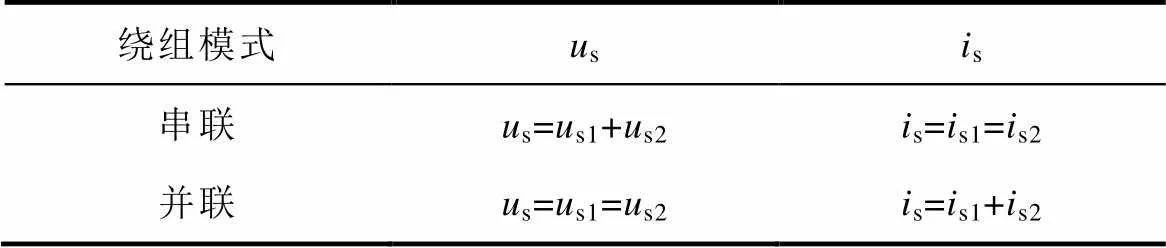
表1 绕组不同模式下系统的电压、电流关系

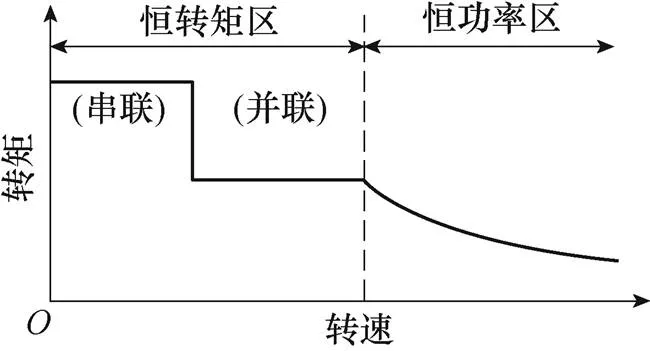
图3 系统的运行特性[3]

另一方面，由图2从逆变器侧看，双绕组PMSM的参数随绕组重构模式不同发生较大变化。由于两套绕组的匝数和参数完全相同，根据电路理论，可得绕组在串联和并联两种模式下整体电机相电阻，交、直电感和永磁体磁链的基本参数关系为

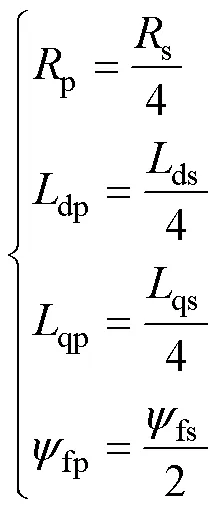
式中，下标s代表串联模式；下标p代表并联模式。

由式（1）可知：串、并联模式下电机参数不同，势必对电机高品质运行带来影响，需要采用现代控制方法，以满足电机运行性能的要求。

从电机侧看，双绕组PMSM可看作两套子电机。每套三相绕组产生的电磁转矩为

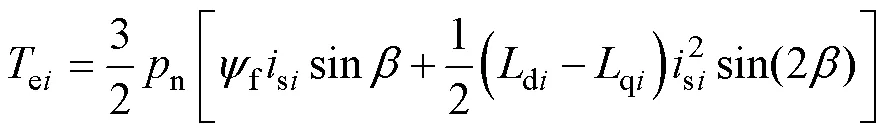
从逆变器侧看，双绕组PMSM无论在串联或并联时均为三相电机，总电磁转矩为各套绕组产生的电磁转矩之和，可得机械方程为

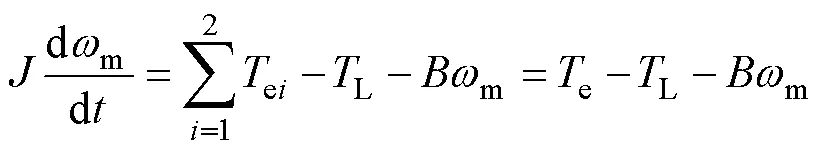
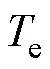
无论为串联还是并联模式，双绕组PMSM总电磁转矩均为两套绕组分别产生的电磁转矩之和。由图2、表1和式（2）、式（3）可知：在电机转速、负载转矩不变时，绕组串/并联时的逆变器侧电流关系为

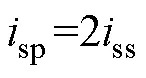
式中，第2个下标s代表串联模式；第2个下标p代表并联模式。

逆变器侧电机电流有效值关系如图4所示。为保持电机输出电磁转矩不变，在绕组重构时要求系统能准确、快速地跟随电机参数变化，满足式（4）的电流关系，否则会引起重构前后转速、转矩波动 较大。

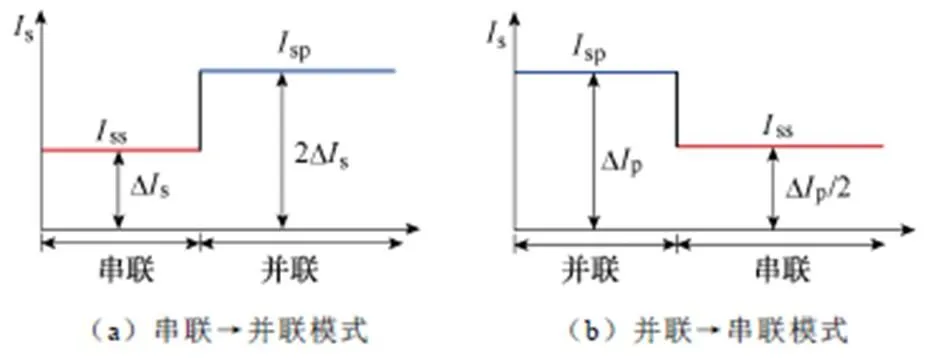
图4 负载转矩相同时逆变器侧的电流关系

2 传统PI控制器的问题分析

基于传统PI控制器，构建双绕组PMSM的双闭环矢量控制系统，图5为系统的传递函数框图。

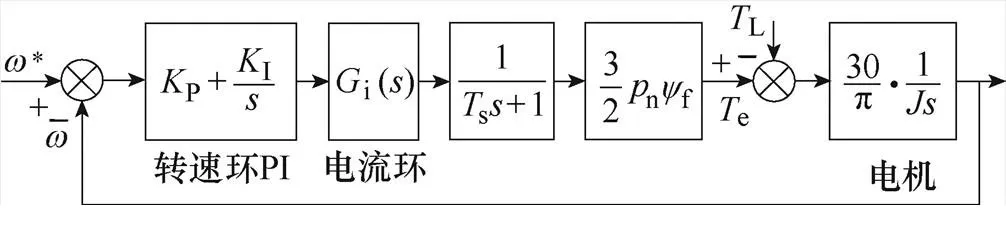
图5 传统PI调节器下的双闭环调速系统

根据“振荡指标法”中的闭环幅频特性峰值最小原则，可设计转速环的PI参数为

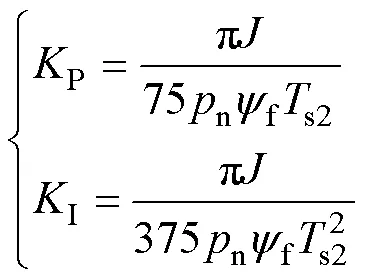
由式（1）和式（5），可得电机绕组处于串联和并联时转速控制器的PI参数关系为

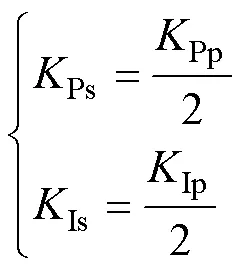
由式（6），绕组在并联模式运行时的PI参数应为串联模式下的2倍，需要根据绕组状态设定不同的PI参数，这是传统PI控制器在该类电机系统中的应用局限性之一。并且采用PI控制器时，转速环输出无法快速满足绕组重构瞬间式（4）的电流关系。例如：由串联重构到并联时，短时内逆变器转速环输出仍为串联时的电流输出、低于并联时对电流的要求，导致电磁转矩不足，造成转速突然降低；相反，由并联重构到串联时，会导致电磁转矩高于负载转矩，造成转速突然升高。

3 转速与抗扰观测复合滑模变结构控制

为了解决传统PI控制器在该类电机控制中存在的问题，本文提出了一种基于转速控制与抗扰观测复合的滑模变结构控制策略，图6为系统结构框图。图6中，转速滑模控制器和滑模抗扰观测器构成了所设计的复合滑模变结构控制策略，以实现双绕组PMSM参数的自适应变化；电流分配模块可根据实际需要选择合适的分配方式，诸如采用最大转矩电流比（Maximum Torque per Ampere, MPTA）或d=0等控制方式分配q、d轴的电流分量。

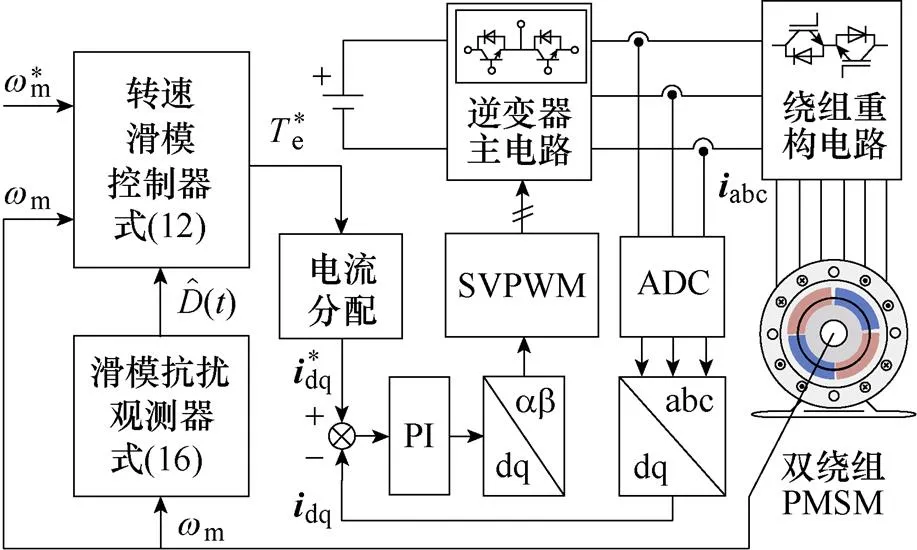
图6 双绕组PMSM复合滑模控制系统框图

3.1 转速滑模控制器设计

为满足绕组各模式下电机的高性能运行，本文设计了一种转速滑模控制器，并对其滑模面选取与控制律进行设计。

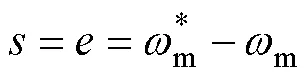
对滑模面求微分得

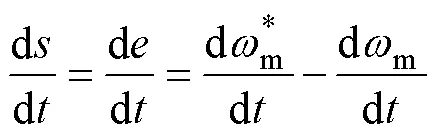
将式（3）代入式（8）可得

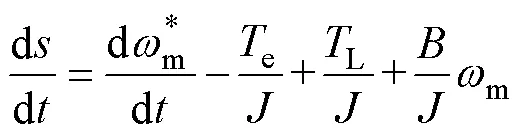
对于控制律的选择，为了有效抑制抖振现象，选取改进控制律[16]

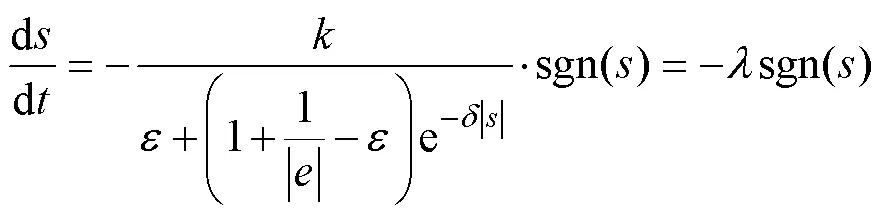
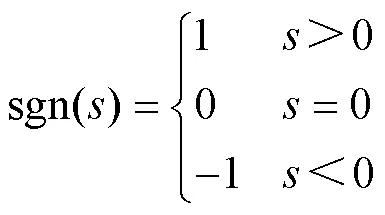
将式（10）代入式（9）得

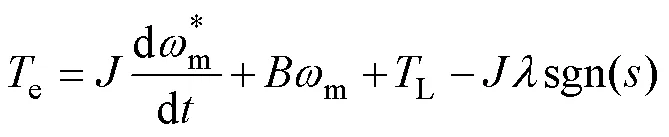
在滑模控制器设计中，整定控制器参数确保系统的稳定性至关重要，最为常用的分析方法为Lyapunov函数法，其稳定性判据为

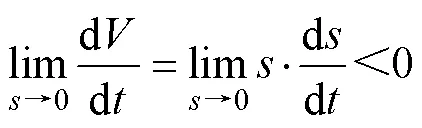
将式（7）、式（10）、式（11）代入可得

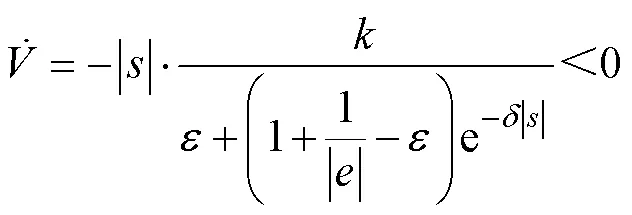
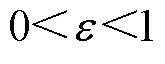
3.2 滑模抗扰观测器设计

为提高双绕组PMSM系统的抗干扰能力，设计了基于前馈补偿的滑模扰动观测器。

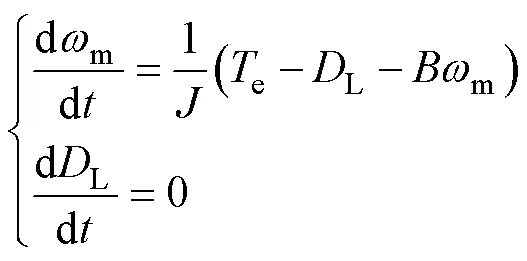
滑模抗扰观测器可描述为

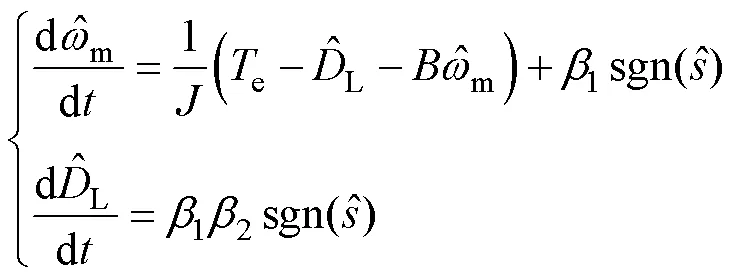
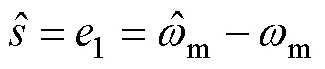
同理，增益系数也需满足一定条件以保证系统的稳定性。由式（15）、式（16）可得方程

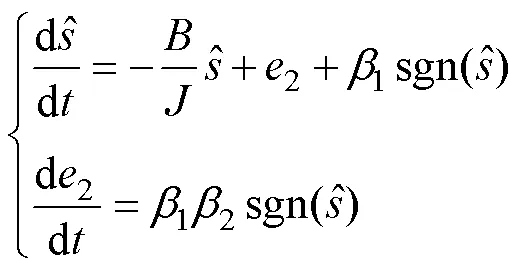
由Lyapunov稳定性判据

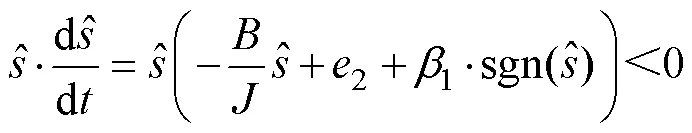
为使式（19）负定，滑模增益1应满足

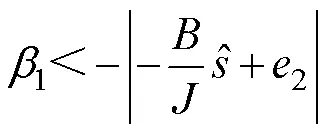
因此，1＜0，可以选取1为

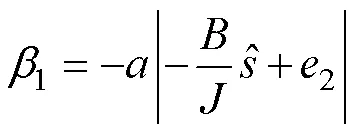
式中，取＞0。

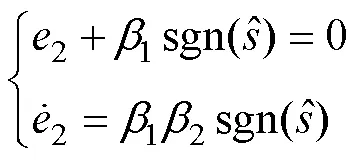
由式（22），可得负载转矩估计误差方程

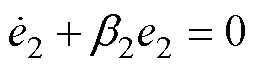
求解得

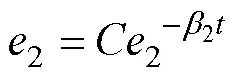
3.3 复合滑模变结构控制器

由上述分析，可得所设计的复合滑模变结构控制器的结构如图7所示。

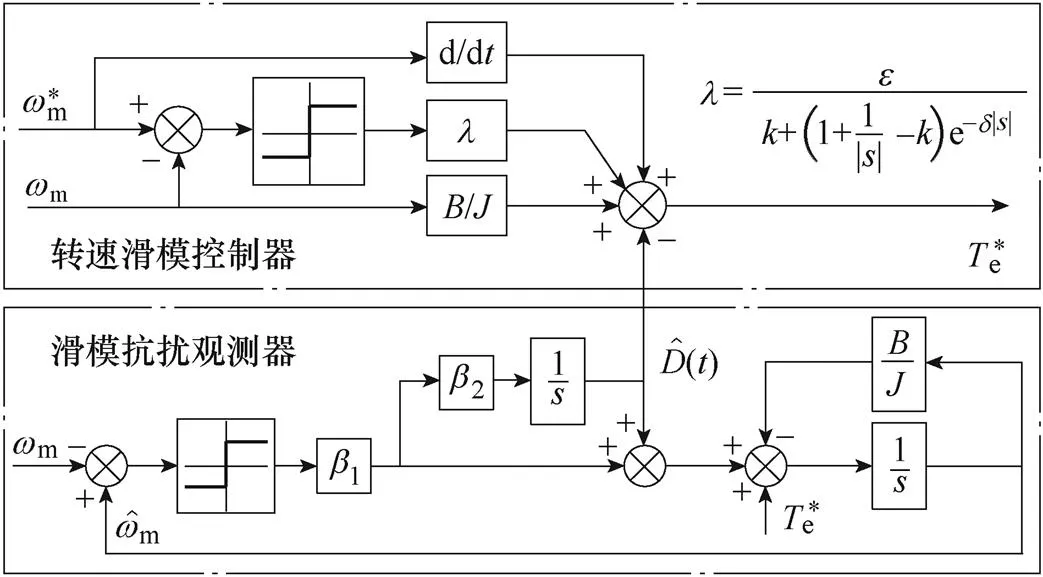
图7 复合滑模变结构控制器

用式（16）滑模抗扰观测器得到的总负载转矩替代式（12）的负载转矩，可得复合滑模变结构控制器输出的电磁转矩给定为

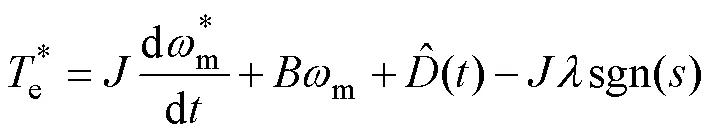
绕组串联或并联时的电磁转矩方程分别为

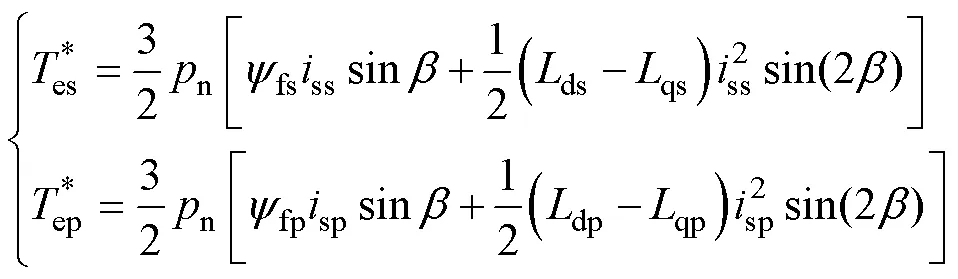
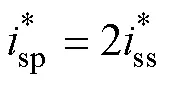
由上述电机转矩-电流关系分析，可得绕组重构瞬间电流给定值式（27）能迅速满足式（4）和图4的电流要求，实现重构瞬间的电流参数自适应匹配，有效抑制重构瞬间的动态波动，可以利用直接切换完成绕组串、并联状态的快速切换。

4 实验结果

为了验证所提滑模变结构控制策略对该类双绕组PMSM的控制性能，搭建了双绕组永磁同步电机小型原理样机的系统实验平台，如图8所示。

逆变器选用TI公司TMS320F28379D套件；重构电路采用图2所示的9开关拓扑结构。为了满足绕组电流双向流动的要求，重构开关选用共发射极IGBT，由两个反向串联的IGBT器件构成，如图9所示。实验时选用英飞凌FF300R12KE4_E型IGBT。

图8 实验平台

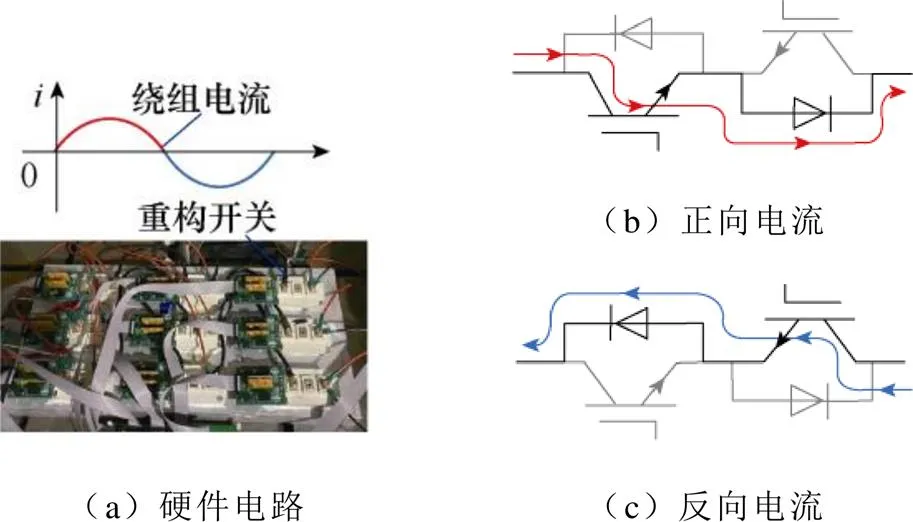
图9 重构开关的电流流向

小型原理样机的主要参数见表2。

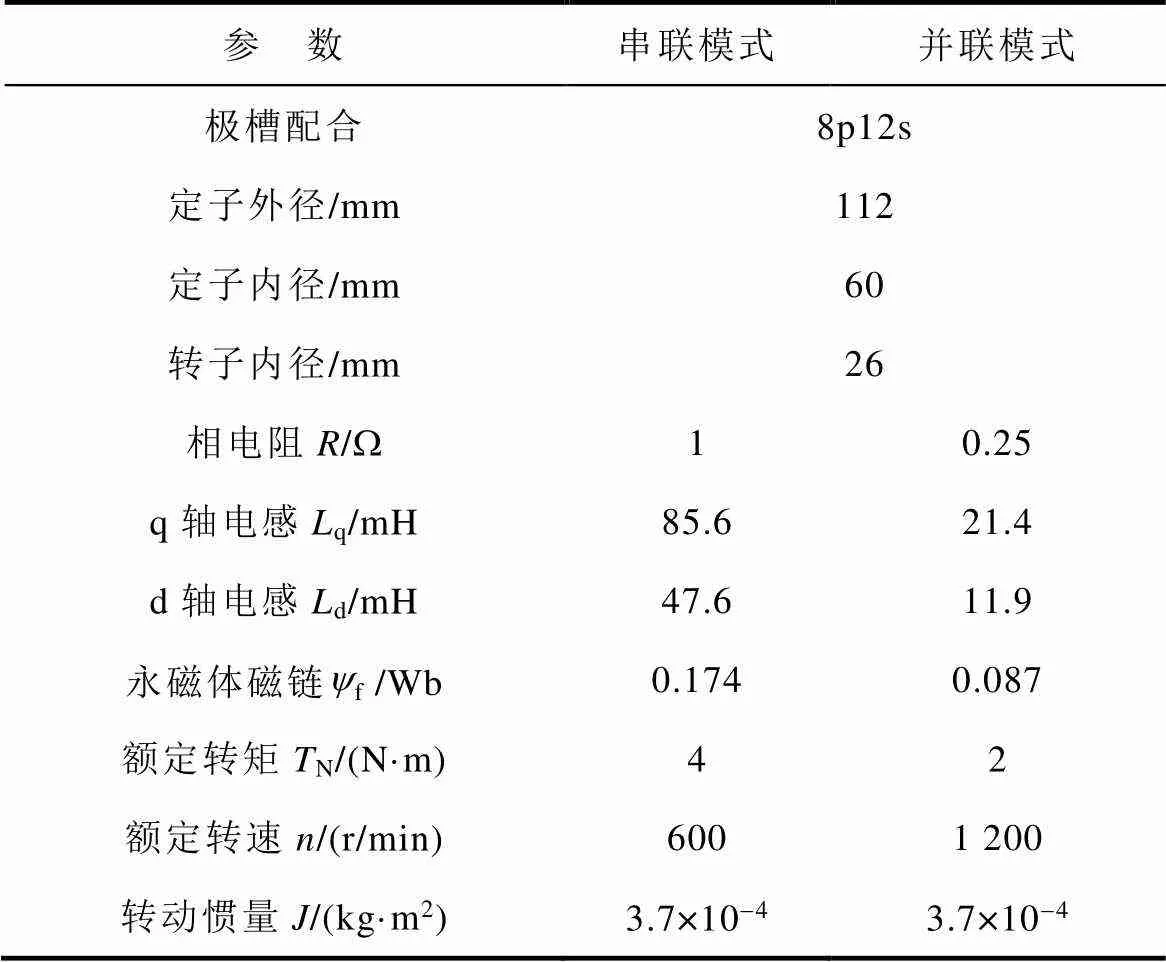
表2 原理型样机主要参数

为了验证本文所提控制策略的可行性和有效性，分别给出了采用传统PI控制和本文所提滑模变结构控制时系统的实验结果。实验中，为了反映电机全工况的运行情况，分别选取绕组串联工况（600r/min@4N·m）、绕组切换工况（1 000r/min@ 2N·m）以及绕组并联工况（1 200r/min@2N·m）三个典型工况进行实验研究。

4.1 串联或并联模式下的实验结果

图10为绕组串联模式、转速600r/min工况下，突加负载转矩0→4N·m或突减负载转矩4→0N·m时的转速响应曲线。

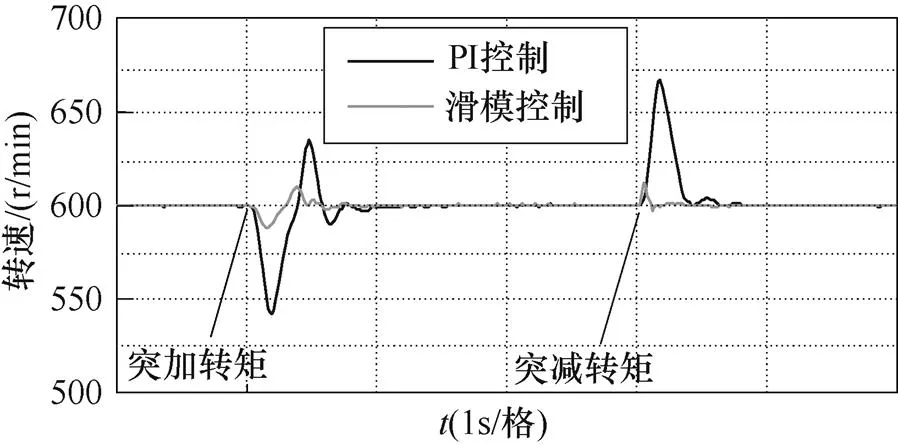
图10 串联模式下突变额定负载的转速响应

图11为绕组并联模式、转速1 200r/min工况下，突加负载转矩0→2N·m或突减负载转矩2→0N·m时的转速响应曲线。

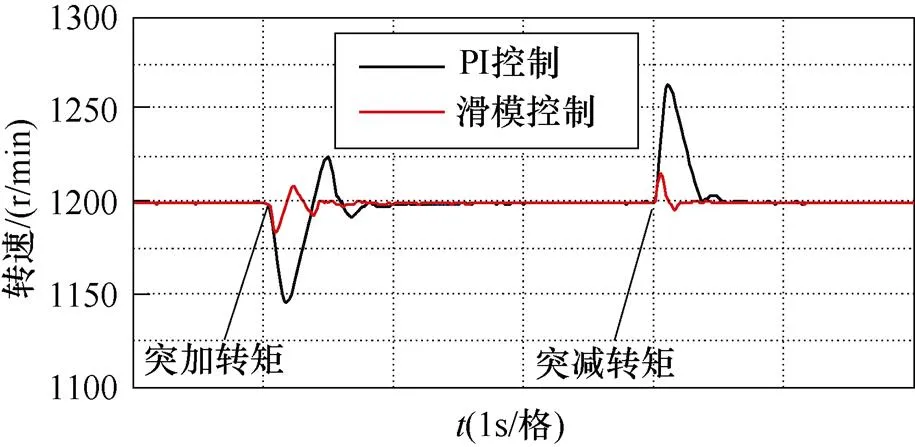
图11 并联模式下突变额定负载的转速响应

从图10、图11可得：绕组在串联或并联模式下突加或突减负载时，采用PI控制时转速波动最大为60r/min左右；而采用本文所提的滑模变结构控制器时，转速波动最大为10r/min左右，能够显著抑制转矩突变时的转速波动；并且能有效减少系统的动态响应时间。

4.2 绕组重构过程的实验结果

实验时，绕组重构工况点的转速为1 000r/min、负载转矩为额定转矩2N·m。图12、图13分别为绕组不同模式重构时的电流响应结果。

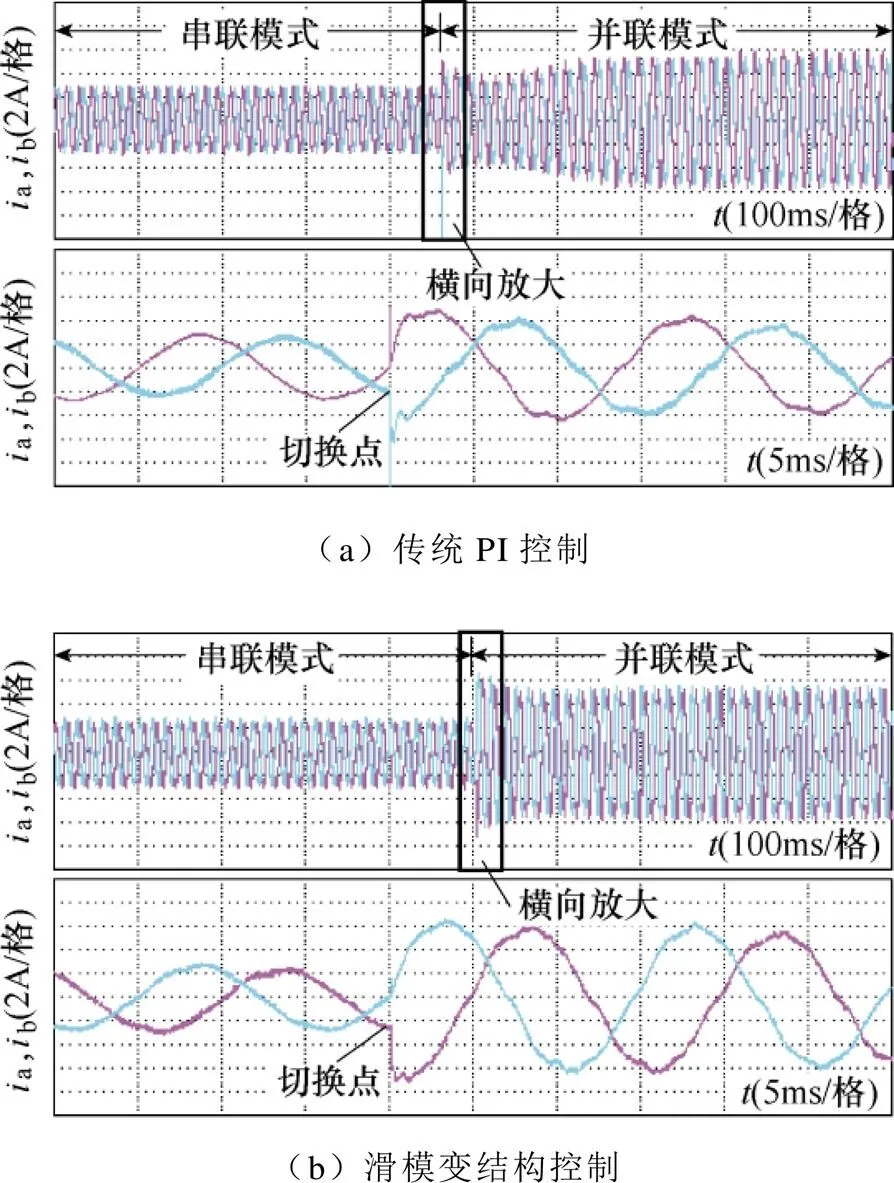
图12 绕组由串联至并联重构过程的电流波形

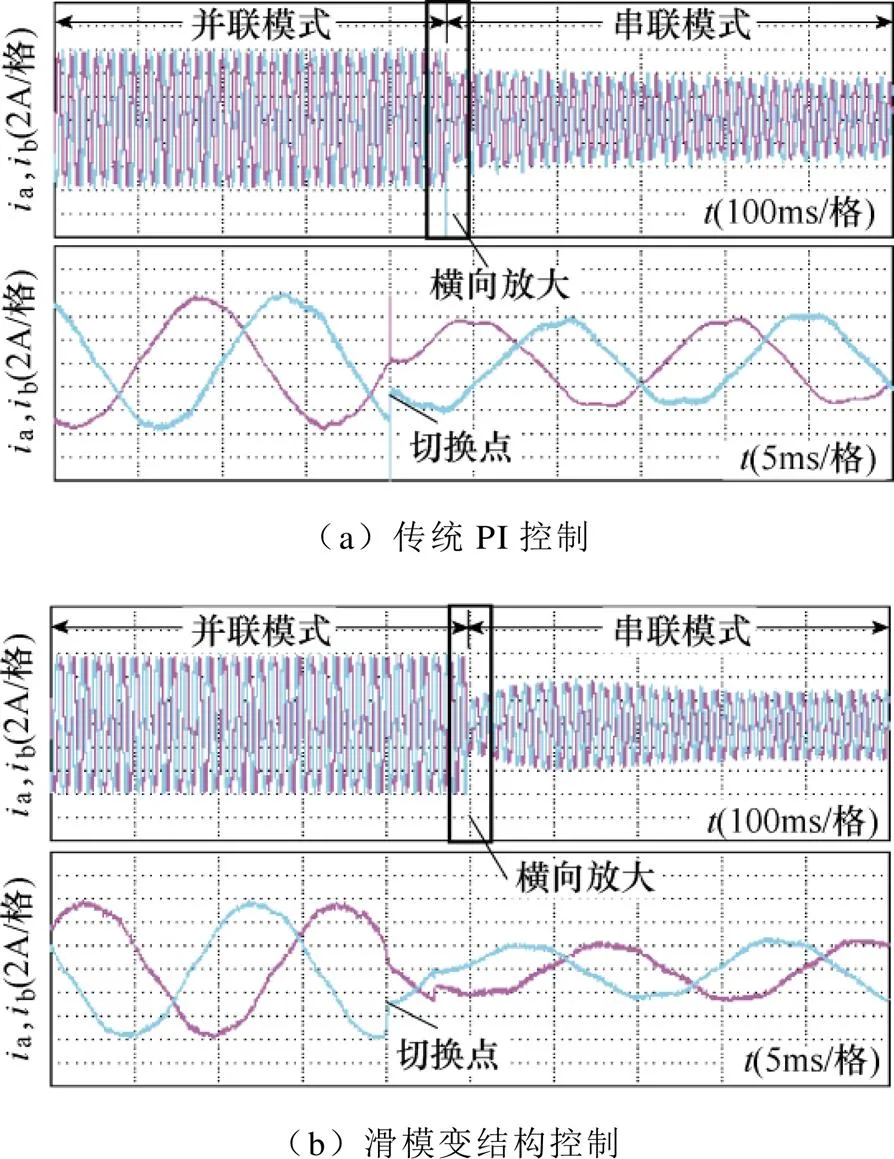
图13 绕组由并联至串联重构过程的电流波形

从图12、图13可得：采用传统PI控制时电流存在突变尖峰；而采用本文所提出的滑模变结构控制方式能够有效抑制重构瞬间的电流突变。

图14为绕组重构过程的转速响应曲线。从图14可得：采用本文所提的复合滑模控制器能显著抑制绕组重构过程的转速波动；并且能显著减少系统的动态响应时间。

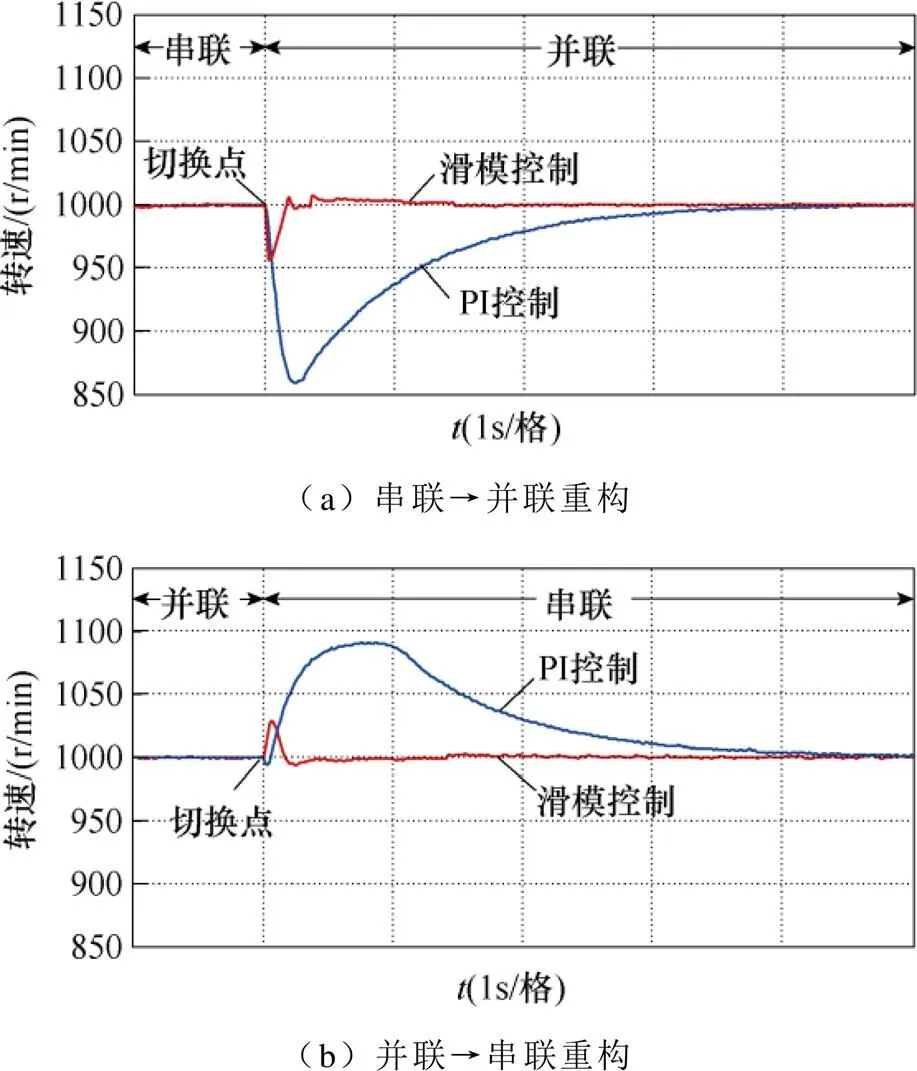
图14 绕组重构过程的转速响应

5 结论

本文所提出的双绕组永磁同步电机滑模变结构控制有效解决了该类电机参数变化和绕组重构存在的问题，实现了该类电机全工况的高品质运行。

1）复合滑模变结构控制器对该类电机参数变化具有强鲁棒性的同时，能够迅速满足绕组重构瞬间电流变化的要求，实现了该类电机典型工况下的参数自适应，提升了系统的动态控制性能。

2）小型样机实验从原理上验证了所提控制策略在该类电机系统中的可行性；为后续根据车辆实际需求设计实用化的宽高效区、宽速域双绕组永磁同步电机系统提供了技术储备。

[1] 王雅玲, 徐衍亮. 基于电动汽车驱动的双定子永磁无刷直流电机绕组换接运行分析[J]. 电工技术学报, 2014, 29(1): 98-103.

Wang Yaling, Xu Yanliang. Winding switching analysis of dual-stator permanent magnet brushless DC motors used in electric vehicles[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 98- 103.

[2] Im S H, Gu B G. A snubberless solid-state tap changer for permanent magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12143-12152.

[3] Huang Hong, Chang Liuchen. Electrical two-speed propulsion by motor winding switching and its control strategies for electric vehicles[J]. IEEE Transactions on Vehicular Technology, 1999, 48(2): 607-618.

[4] Hsieh M F, Hsu F S, Dorrell D G. Winding change- over permanent-magnet generators for renewable energy applications[J]. IEEE Transactions on Magnetics, 2012, 48(11): 4168-4171.

[5] 李垣江, 董鑫, 魏海峰, 等. 表贴式永磁同步电机转速环复合PI无位置传感器控制[J]. 电工技术学报, 2020, 35(10): 2119-2129.

Li Yuanjiang, Dong Xin, Wei Haifeng, et al. Sensor- less compound PI control for surface permanent magnet synchronous motor speed regulation system[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2119-2129.

[6] Liu Yang, Xiahou Kaishun, Wang Lei, et al. Switching control of GSC of DFIGWTs for disturbance rejection based on Bang–Bang control[J]. IEEE Transactions on Power Delivery, 2018, 33(6): 3256-3259.

[7] Chaoui H, Khayamy M, Aljarboua A A. Adaptive interval type-2 fuzzy logic control for PMSM drives with a modified reference frame[J]. IEEE Transa- ctions on Industrial Electronics, 2017, 64(5): 3786- 3797.

[8] 赵希梅, 金鸿雁. 基于Elman神经网络的永磁直线同步电机互补滑模控制[J]. 电工技术学报, 2018, 33(5): 973-979.

Zhao Ximei, Jin Hongyan. Complementary sliding mode control for permanent magnet linear synchronous motor based on Elman neural network[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(5): 973-979.

[9] 陈卓易, 屈稳太. 基于PID型代价函数的永磁同步电机模型预测电流控制[J]. 电工技术学报, 2021, 36(14): 2971-2978.

Chen Zhuoyi, Qu Wentai. Model predictive current control for permanent magnet synchronous motors based on PID-type cost function[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2971- 2978.

[10] Niu Shuangxia, Luo Yixiao, Fu Weinong, et al. Robust model predictive control for a three-phase PMSM motor with improved control precision[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 838-849.

[11] 王勃, 王天擎, 于泳, 等. 感应电机电流环非线性积分滑模控制策略[J]. 电工技术学报, 2021, 36(10): 2039-2048.

Wang Bo, Wang Tianqing, Yu Yong, et al. Nonlinear integral sliding mode control strategy for current loop of induction motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2039-2048.

[12] Qu Lizhi, Qiao Wei, Qu Liyan. Active-disturbance- rejection-based sliding-mode current control for permanent-magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 751-760.

[13] Yeam T I, Lee D C. Design of sliding-mode speed controller with active damping control for single- inverter dual-PMSM drive systems[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(5): 5794- 5801.

[14] Lian Chuanqiang, Xiao Fei, Gao Shan, et al. Load torque and moment of inertia identification for permanent magnet synchronous motor drives based on sliding mode observer[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5675-5683.

[15] Lu Wenqi, Zhang Zhenyi, Wang Dong, et al. A new load torque identification sliding mode observer for permanent magnet synchronous machine drive system[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7852-7862.

[16] Zhang Xiaoguang, Sun Lizhi, Zhao Ke, et al. Non- linear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J]. IEEE Transactions on Power Electro- nics, 2013, 28(3): 1358-1365.

[17] Wang Yaoqiang, Feng Yutao, Zhang Xiaoguang, et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4117-4126.

[18] 熊林云, 王杰. 永磁同步电机电能质量分数阶滑模控制[J]. 中国电机工程学报, 2019, 39(10): 3065- 3074.

Xiong Linyun, Wang Jie. Fractional order sliding mode control of PMSG wind turbine for power quality enhancement[J]. Proceedings of the CSEE, 2019, 39(10): 3065-3074.

[19] Fulton D A. Switch module for an electric machine having switchable stator windings: US8415910[P]. 2013-04-09.

[20] Tang Lixin, Burress T, Pries J. A reconfigurable- winding system for electric vehicle drive appli- cations[C]//2017 IEEE Transportation Electrification Conference and Expo, Chicago, IL, USA, 2017: 656- 661.

[21] Nipp E. Permanent magnet motor drives with switched stator windings[D]. Stockholm: Royal Institute of Technology, 1999.

Sliding Mode Variable Structure Control of a Dual-Winding Permanent Magnet Synchronous Motor

（School of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China）

Dual-winding permanent magnet synchronous motor (PMSM) can improve the operating range by reconfiguring the windings of the series and parallel modes. However, the motor parameters variation in different winding modes could cause the traditional PI controller to be unable to satisfy the high-quality operation requirements. According to the operating characteristics of this type of motor, this paper studies a composite sliding mode variable structure controller that integrates speed loop control and anti-disturbance observation, which could effectively suppress the dynamic fluctuation of speed caused by motor parameter variation and winding reconstruction. Firstly, the working mechanism of the dual-winding PMSM in different modes and the reasons for the speed fluctuation during winding reconstruction are analyzed. Secondly, a sliding mode variable structure controller is designed to realize the self-adaptation of control parameters and quickly meet the reconstruction of the instantaneous current relationship to suppress dynamic fluctuations. Finally, a comparative experiment is carried out under typical working conditions for the scheme using PI controller and the sliding mode variable structure controller through a miniature principle prototype, which verifies the effectiveness and feasibility of the proposed control strategies.

Permanent magnet synchronous motor (PMSM), dual-winding construction, winding reconstruction, sliding mode variable structure control

TM351

10.19595/j.cnki.1000-6753.tces.211513

国家自然科学基金资助项目（51307032, 52277040）。

2021-09-27

2022-03-08

于艳君 男，1979年生，博士，教授，研究方向为特种电机控制。

E-mail: yuyanjun@hit.edu.cn

柴 凤 女，1973年生，博士，教授，研究方向为特种电机系统。

E-mail: chaifeng@hit.edu.cn（通信作者）

（编辑 郭丽军）