半夏块茎物理特性研究及离散元仿真参数标定

杨贵川，张富贵，郑乐，王震，孔曼曼，章鑫鹏

（贵州大学机械工程学院，贵阳 550025）

半夏（Pinellia ternata）具有燥湿化痰、降逆止呕、消痞散结的功效，全国第三次中药资源普查显示，在588 个抽样处方中，半夏在处方中出现的频率位于第22 位；国家210 个法定汉方中含半夏的有46 个，其应用量约占第21 位，临床应用广泛，具有十分重要的药用价值[1-3]。半夏在贵州广泛种植，种植面积、产量均位居全国前列，还拥有“大方圆珠半夏”和“赫章半夏”2 个国家地理标志保护产品。半夏块茎具有极高的经济价值，目前成品半夏块茎市场价格在80～100 元·kg-1，极大地助力了当地脱贫攻坚工作[4-5]。半夏的种植方式主要为条播和垄上撒播，为了保证半夏品质，贵州地区采用垄上撒播种植模式（在半夏播种初期施用有机肥和复合肥，后期不再对其进行除草、杀虫作业，通过高密度播种的方式抑制杂草生长，保证产量）模拟野生生长环境，撒播作业通过人工进行，费时、费力且种植成本居高不下。因此为了省工降本，进一步扩大生产规模，需尽快实现机械化作业。

部分半夏产区采用链勺式排种器、外槽轮式排种器等设备进行条播作业，存在易伤种、作业幅宽过小、播种均匀性差、播种密度无法达到作业要求等问题。离散元仿真广泛应用于分析颗粒物料与设备交互作用下的运动、受力等，可以缩短设备的研发周期，降低研发成本。为了设计适应贵州地区半夏种植特点的半夏撒播排种器，有必要对半夏块茎参数进行仿真标定。文恩杨等[6-8]设计了大蒜播种机，并通过离散元仿真优化了关键部分的结构参数；刘文政等[9-11]对微型马铃薯进行了离散元仿真标定，并确定了基于振动排序的马铃薯微型种薯播种机的最佳振动频率范围；温翔宇等[12]通过离散元仿真试验优化了气力变量配比施肥装置；刘彩铃等[13-14]基于EDEM 离散元仿真对离心甩盘撒肥器的性能进行了分析与试验，确定了最佳甩盘转速、喂入量、喂入角和喂入位置角；吴孟宸等[15]对花生颗粒进行了离散元仿真标定，并验证了花生排种器的排种性能；赖庆辉等[16-19]基于三七种苗的离散元仿真参数设计了滚筒板齿式三七种苗分离装置、超窄行气吸式三七精密排种器及凸包异形孔窝眼轮式人参精密排种器，并进行了优化设计。

本研究采用实际接触试验确定仿真参数试验范围，结合最陡爬坡试验和Box-Behnken 试验对半夏的离散元仿真参数进行标定；通过压缩试验对半夏的本征物理特性进行测定分析，建立了半夏离散元仿真模型，以期为半夏撒播排种器提供离散元仿真参数。

1 材料与方法

1.1 试验材料

本研究以贵州省赫章县种植基地的半夏块茎为试验材料，块茎近似椭球形，随机选取100 颗，利用游标卡尺对其三轴尺寸进行测量，根据下式求出半夏的等效直径。

式中，d为等效直径，L为长度，W为宽度，T为厚度。

采用软件Origin 软件拟合得出半夏等效直径的分布规律，半夏等效直径为正态分布（图1），峰值为16.8 mm。根据所测结果，对比实际半夏块茎在EDEM 中组合创建半夏的仿真模型（图2），模型的物理特性参数根据测定参数设定。

图1 半夏等效直径分布Fig.1 Equivalent diameter distribution of P.ternata stems

图2 半夏块茎及仿真模型Fig.2 Tuber and simulated particle model

1.2 半夏基本物理特性参数测定

用电子秤称取播种期半夏质量（上1 年度10月份收获的半夏，次年3月播种），将半夏放入DHG-9741A 型电热恒温干燥箱（上海精宏实验设备有限公司），105 ℃烘烤至恒重，计算半夏含水率。在500 mL 的量筒中注入300 mL 清水，将鲜半夏放入量筒中使其自然沉入水底，读取量筒内水的体积变化量，计算半夏密度。

根据泊松比的定义，对半夏进行压缩试验。由于半夏形状不规则，因此将半夏用内径10 mm、高40 mm 的环刀和美工刀切割成直径10 mm、高10 mm 的规整试样。将试样用QJ211S 型农作物专用试验机（上海倾技仪器仪表科技有限公司）对试样进行压缩试验，并测量试样受压变形后的横向及纵向应变量[15,20-21]。分别以1、3、5 mm·min-1的速率压缩试样，每个速率重复9 次，试样产生塑性变形前停止压缩，用电子游标卡尺测量其横向与纵向变形尺寸，计算泊松比。

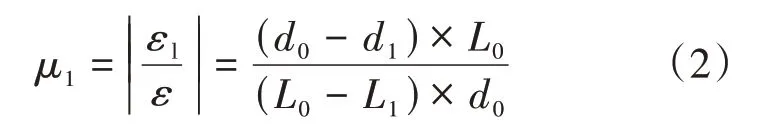
式中，μ1为泊松比；εl为横向应变；ε为纵向应变；L0为试样原始长度，mm；L1为压缩变形后试样长度，mm；d0为试样初始直径，mm；d1为试样变形后直径，mm。弹性模量E计算公式如下。

式中，E为弹性模量，MPa；ΔF为压力变化量，N；A0为试样横截面积，mm2。

1.3 碰撞恢复系数标定

分别用尼龙绳绑住球形半夏胚芽，尼龙绳另一端固定在同一点，固定点背景为A3 坐标纸；为便于观察碰撞过程，应尽量选择大的摆动半径，取摆动半径为360 mm（由于半夏中心点难以确定，因此试验过程中，测量拉绳与半夏的捆绑点高度变化，代替中心点高度变化）。如图3 所示，将半夏a 沿圆周方向拉起一定高度并释放，使其自由摆动最终与半夏b 发生碰撞，a、b 沿周向运动，最终动能全部转换为重力势能（试验过程由高速摄像机记录），通过背景坐标纸测量a、b 到零点（a、b 自然悬垂点）的垂直距离，根据式（4）计算碰撞恢复系数。

图3 半夏-半夏碰撞仿真试验Fig.3 Simulation test of pinellia stalk and pinellia stalk collision

式中，e1为碰撞恢复系数；vb为半夏b 的瞬时分离速度，mm·s-1；va为半夏a 的瞬时分离速度，mm·s-1；v0为半夏a的瞬时接近速度，mm·s-1；H0为半夏a初始释放高度，mm；Ha为半夏a极限爬升高度，mm；Hb为半夏b极限爬升高度，mm。

试验过程中发现，将半夏从初始位置拉升抬高100 mm处时将超出测量范围，为确保高速相机能够清晰地记录碰撞全过程及坐标纸标尺，取H0分别为30、50 mm，重复30 次碰撞试验，测得Ha分别为（3.2±0.5）和（3.75±1）mm，Hb分别为（16.56±3）和（25.70±6）mm，碰撞恢复系数e＇1分别为（0.469 0±0.05）和（0.474 0±0.05）mm，实际试验测得的e＇1变异系数为0.75%，表明H0对碰撞恢复系数并无影响，因此取50 mm 作为仿真试验初始释放高度（H0）。

在EDEM 仿真试验（图3）中，采用中心半径为360 mm 的半圆形空心圆筒以控制半夏的摆动轨迹（代替拉绳）。H0为初始释放高度，ya为颗粒a 的极限爬升高度，yb为颗粒b 的极限爬升高度，圆筒内径为15 mm，分别在圆筒的轨道铅锤方向管道中心点和距离该点50 mm 处各生成1 粒球形半夏颗粒模型a、b,为避免摩擦力对仿真结果产生影响，将颗粒模型与管道模型间的摩擦系数设置为0。根据仿真结果分别建立回归模型，结合实际试验结果标定出半夏-不锈钢间的碰撞恢复系数e1。

同理，分别在40、80、120 mm 处释放半夏，测得半夏-钢板的反弹平均高度H1分别为(16.47±3.52)(29.33±2.43)(45.67±2.21) mm，根据式（5）计算出半夏-不锈钢实碰撞恢复系数e＇2分别为（0.63±0.05）（0.60±0.03）（0.61±0.03），变异系数为2.49%，变异系数较小，表明半夏的释放高度对半夏-不锈钢板间的碰撞恢复系数影响越小。

式中，H＇0为半夏跌落高度，mm；H1为半夏极限回弹高度，mm。

选择120 mm 作为仿真试验释放高度开展标定，通过实际试验表明半夏与不锈钢板间的碰撞恢复系数在0.58～0.70 之间。在EDEM 仿真过程中，不锈钢的密度8 000 kg·m-3，泊松比为0.29、弹性模量7 500 MPa[22]，为避免摩擦系数的影响，将摩擦系数设定为0，将半夏-不锈钢板的碰撞恢复系数设定在0.58～0.70，步长为0.02。根据仿真结果分别建立回归模型，结合实际试验结果标定出半夏-不锈钢间的碰撞恢复系数e2。

1.4 摩擦因素标定

1.4.1 半夏-不锈钢静摩擦因素标定 将4 个体积相当的半夏用透明胶带粘贴在一起（防止半夏发生滚动），通过斜面滑动试验测定半夏-不锈钢的静摩擦系数，利用数显角度尺（精度0.05°，量程0°～360°）测量钢板与水平面间的夹角，静摩擦系数与抬升平面倾角间的关系如下。

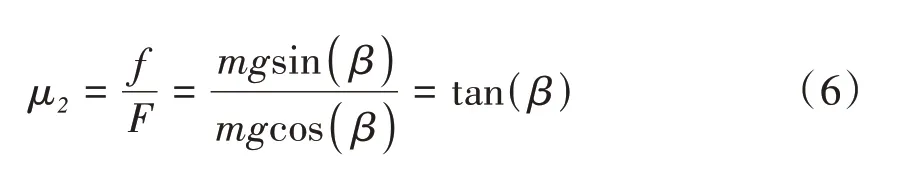
式中，μ2为半夏-不锈钢板静摩擦系数；f为摩擦力，N；F为颗粒平行于斜面的分力，N；β为斜面与水平面的夹角，测量5次取均值，β为31.55°。

由于在EDEM 软件仿真过程中，其他仿真参数对静摩擦因素并无影响，因此引用文献[11]对离散元仿真颗粒模型静摩擦系数标定的回归方程。

式中，y2为倾角，x2为块茎与钢板间的静摩擦系数，取y2=31.55°代入式（7），可得半夏-不锈钢静摩擦因素μ2。

1.4.2 滚动摩擦因素及半夏间静摩擦系数标定由于滚动摩擦系数、颗粒间的静摩擦系数难以直接进行测定，因此采用堆积角试验进行间接测量，颗粒堆积角是物料流动性、物料摩擦系数等本征物理特性的宏观体现，物料的静摩擦系数、滚动摩擦系数等物理特性参数对堆积角的角度大小影响显著[23-26]，因此通过无底圆筒（内径120 mm，高度360 mm）提升试验测定半夏在不锈钢板上的堆积角[27]。圆筒提升试验获取堆积角，重复5 次取平均值，测得堆积角为（37.55°±1°）。

用EDEM 软件对上述试验作重复仿真试验，设计最陡爬坡试验确定半夏-半夏摩擦系数、半夏-不锈钢滚动摩擦系数取值范围，初始值为0，以0.03为步长逐渐增加，进行爬坡试验（仿真过程中其他参数采用文中已标定的数值）。用Box-Behnken 试验确定显著性影响因数，并根据试验结果建立回归模型，对回归模型进行二次优化，最终结合实际试验标定摩擦系数。

2 结果与分析

2.1 半夏本征物理特性参数分析

通过烘干试验测得半夏含水率为62.23%，通过浸液试验测得半夏的体积，并测量半夏的质量，最终求得半夏的密度为1 210 kg·m-3。经压缩试验得到不同压缩速率下的泊松比及弹性模量，结果如表1 所示。通过对比分析得知，不同压缩速率下的半夏泊松比μ1变异系数为1.85%、弹性模量E变异系数为9.01%，泊松比及弹性模量变异系数较小，因此取3 种压缩速率下的平均值，半夏的实际泊松比μ1=0.373 1、弹性模量E=5.757 1 MPa。

表1 半夏压缩试验结果Table 1 Result of P.ternata tuber compression

2.2 半夏-半夏碰撞恢复系数仿真参数分析

为保证仿真试验不受摩擦力的影响，将圆筒轨道-半夏模型、半夏模型间的摩擦系数、碰撞恢复系数设为0；用EDEM 后处理功能测量半夏a、b碰撞后的最大提升高度ya、yb，结果如表2 所示。以半夏碰撞恢复系数x为自变量，半夏a、半夏b碰撞后的最大爬升高度ya、yb为因变量。用Origin对仿真结果进行二次多项式拟合，得到式（8）。

表2 半夏-半夏碰撞仿真试验结果Table 2 Simulation test results of P.ternata-P.ternata collision

拟合方程决定系数分别为=0.957 1、=0.992 2，均接近1，表明拟合方程准确可靠。将Ha=3.75 mm、Hb=25.70 mm 代入式(8)，联立可得x=0.472 0。将0.472 0 作为半夏间恢复系数，在H0=50 mm 为初始条件下各做3 次重复仿真试验，得半夏a 碰撞后上升的最大高度平均值ya=4.83 mm，与实际试验平均值的相对误差为22.36%；半夏b 碰撞后上升的最大高度平均值yb=26.27 mm，与实际试验测量值相对误差为2.17%；仿真碰撞恢复系数x=0.472 0 与真实试验测量中得碰撞恢复系数e＇1=0.474 0，二者相对误差仅为0.42%；表明仿真参数与实际试验结果差异较小，因此取半夏间仿真碰撞恢复系数e1=0.472 0。

2.3 半夏-不锈钢的碰撞恢复系数仿真参数分析

半夏-不锈钢板的碰撞仿真试验结果如表3所示。以恢复系数x1为试验因数，回弹高度y1为评价指标，对结果进行曲线拟合，建立拟合方程。

表3 半夏-不锈钢板碰撞仿真试验结果Table 3 Simulation test result of P.ternata-stainless steel plate collision

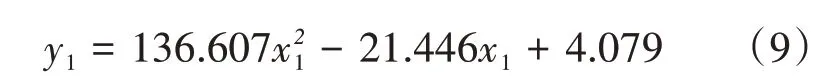
决定系数R2=0.999 9，接近于1，表明拟合方程可信度高。将y1=45.67 带入方程（9）得到x1=0.635 8。以0.635 8 为半夏-不锈钢板碰撞恢复系数，分别在H0为40、80、120 mm 释放高度下各做3 组重复仿真试验，得块茎平均仿真回弹高度H1分别为16.77、31.24、45.82 mm，与真实试验条件下得到的反弹高度相对误差分别为1.82%、6.51%、0.33%，x1与e2＇间的相对误差为3.89%误差较小，故取半夏-不锈钢板间的仿真碰撞恢复系数为e2=0.635 8。

2.4 半夏-不锈钢板静摩擦系数仿真参数分析

将y2=31.55°带入式（7）中，得x2=0.615 4，将0.615 4 设置为半夏-不锈钢板间的静摩擦系数，其他摩擦系数设置为0，进行3次重复斜面滑动仿真试验，得到不锈钢板倾角分别为31.58°、31.57°、31.57°，取平均值为31.573 0°，与实际试验值31.550 0°的相对误差为0.643%。表明标定后的仿真结果与实际试验结果差异较小，因此取半夏-不锈钢板将的静摩擦系数μ2=0.615 4。

2.5 半夏-半夏静摩擦系数对滚动摩擦素的影响

2.5.1 半夏-半夏静摩擦系数对堆积角的影响爬坡试验结果如表4所示，随着A、B、C增加，堆积角逐渐增大，真实试验与仿真试验得到的半夏堆积角的相对误差先减小后增加。在6 号水平时，该相对误差最小，由此可知最优值区间在6 号水平附近，因此选取6 号水平为中心点，5 号、7 号水平为低、高水平进行后续的响应面设计。

表4 最陡爬坡试验Table 4 Steepest climbing test

利用Design-Expert 软件设计Box-Behnken 试验，根据仿真试验结果（表5）建立回归模型（式10）。

表5 堆积角Box-Behnken试验结果Table 5 Result of stacking angle Box-Behnken test

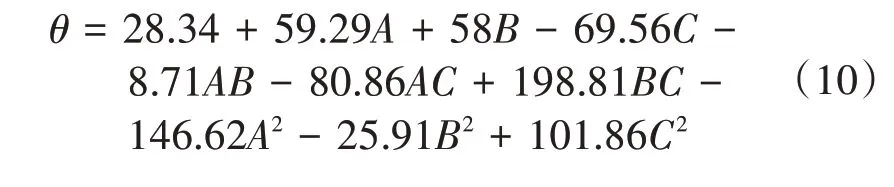
方差分析（表6）表明，B的二次项以及BC交互项对堆积角影响极为显著；拟合方程的决定系数R2=0.995 6，校正决定系数R2adj=0.987 8，二者均接近1，表明拟合方程可靠度高；精密度为37.422 2，表明该模型具有良好的精确度。

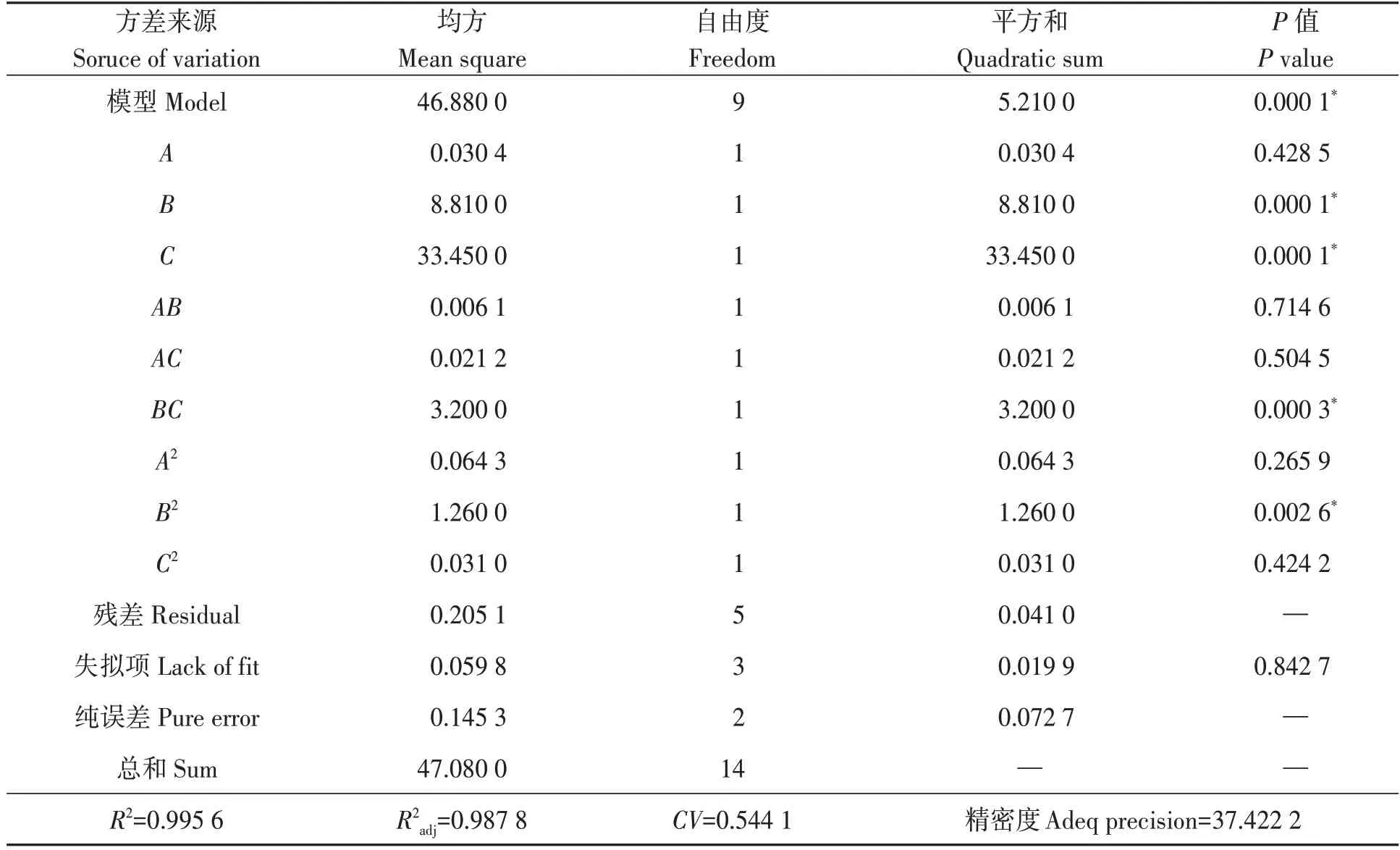
表6 堆积角试验方差分析Table 6 Analysis of variance in the stacking angle test

剔除表6 中对堆积角仿真试验影响不显著的项，对二阶回归模型进行优化，结果如表7 所示，得到优化后的回归模型（式11）。

表7 二次优化后回归模型Table 7 Regression model after second optimization

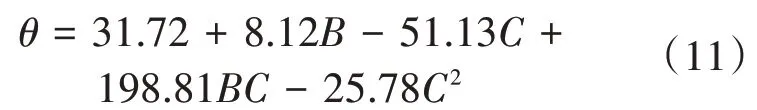
优化后的回归模型变异系数为1.390 0%，决定系数R2=0.979 4，校正决定系数R2adj=0.967 9，二者都接近1，模型精密度增大到56.052 9，表明拟合方程可靠度高，因此可利用该回归方程可以用来预测半夏的堆积角。

2.5.2 回归模型寻优求解及仿真验证 通过表7可知，交互项BC对半夏的堆积角影响显著。当A=0.15时，应用Design-Expert软件绘制BC交互项的响应曲面，如图5 所示，当BC同时增大或减小时半夏堆积角变化显著。通过Design-Expert软件对优化后的回归模型进行目标寻优求解，以实际试验时测得的半夏平均堆积角37.55°为目标，由于A不显著，取中间水平0.15，通过Design-Expert求解可得：B为0.554，C为0.157。为验证标定参数的准确性，采用上文中标定的各参数数值进行无底圆筒提升仿真试验，获得半夏堆积角，如图6所示，得到堆积角分别为37.80°、37.29°、37.43°，取平均值为37.51°，与实际堆积角的相对误差为0.107%，表明仿真结果与实际试验无显著差异。

图5 BC交互项响应曲面Fig.5 BC interaction term response surface

图6 半夏堆积角Fig.6 Pile of stems of P.ternata

3 讨论

本文以贵州赫章半夏为研究对象，建立了半夏的EDEM 仿真模型，并测定了半夏的含水率为62.23%；采用浸液试验测定了半夏的密度为1 210 kg·m-3，半夏的泊松比μ=0.373 1、弹性模量E=5.757 1 MPa。当压缩应力超过标定参数时，半夏将发生塑性形变，因此在设计半夏排种器时，应考虑半夏受力状态，避免破坏半夏导致发芽率降低。

利用实际物理试验结合EDEM 仿真试验的方法测定半夏间的碰撞恢复系数、半夏-不锈钢板间的碰撞恢复系数、半夏-不锈钢板间的静摩擦系数，对试验结果进行回归分析，并建立回归方程，分析结果表明：半夏-半夏间碰撞恢复系数e1=0.472 0，半夏-不锈钢板间碰撞恢复系数e2=0.635 8，半夏-不锈钢板间的静摩擦系数μ2=0.615 4。

由于A、B、C难以直接进行测量，采用实际圆筒提升试验结合最陡爬坡仿真试验，筛选出中心水平，并用Design-Expert软件设计Box-Behnken试验，根据试验结果建立回归方程，对回归方程进行方差分析，并对回归模型进行二次优化，最终获得到A=0.150、B=0.554、C=0.157。

颗粒物料的结拱与物料的直径、摩擦因、含水率等因数有关[28-29]，目前对物料结拱条件的理论性研究较少，离散元仿真可以用于研究半夏结拱形成条件，对半夏进行离散元仿真参数标定及物理特性研究，可以为半夏排种器结构尺寸确定提供依据，同时也为半夏排种器离散元仿真分析提供了参数依据。