基于增益自适应超螺旋滑模理论的无人机控制
周齐贤, 王 寅, 孙学安
(南京航空航天大学 航天学院, 南京 211106)
现如今,无人驾驶飞行器,即无人机(UAV)已在民用领域发挥重要作用,可以飞得更快、更远、更高,并在人工难以到达的位置作业.民用无人机能够携带包括相机在内的设备并运送小载荷物品,因此可以进行监视、医疗保健、科学研究和探索、作物喷洒、野生动物监测、媒体报道和应急服务等活动.此类无人机具有快速机动性的同时,也具有耦合性和非线性强的特点.
无人机全包线飞行过程具有难以控制的不确定性,因此,为保证无人机的稳定性和安全性,飞行控制器性能设计要求极高.近10多年来,国内外众多研究人员和学者采用多种控制方法进行相关领域研究.王家琪等[1]改进滑模面趋近律,基于干扰观测器的滑模控制律抑制无人机高速飞行过程中的不确定性和外部干扰,加快系统的收敛速度.黄金杰等[2]将时变参数变化范围划分为具有多个重复区域的子空间,在非重复区域单独调用相应的状态反馈控制器,在重复区域加权调用控制器,基于平稳切换的策略设计具有鲁棒H∞性能的无人机控制系统.孙冰等[3]采用自适应反步设计思想,通过使用径向基函数网络对无人机舵控指令进行误差逼近,实现无人机抗饱和非线性飞行控制.刘志豪等[4]针对垂直起降的无人机控制问题,提出最快模式转换定高控制策略,通过模拟分析和实验手段与比例积分微分(PID)控制策略做对比,证明该控制策略相较于常规控制策略具有显著的优越性.Huang等[5]采用深度强化学习算法中的双深度Q学习方法,通过建立无人机的非线性姿态动力学模型和相应的马尔可夫决策过程,训练控制器使其具有优秀的固定翼飞行器姿态控制能力.Zhi等[6]提出一种基于鲁棒伺服线性二次型调节器控制和卡尔曼滤波器的桨距角控制器.然而,如果飞行状态偏离标称条件,这些控制器的性能就会下降.非线性控制技术通过对整个飞行状态使用单个控制器来改善性能.Hirano等[7]提出推力矢量系统方法解决反步控制方法中虚拟控制量难以确定的问题,并设计无人机的非线性控制器.Oliveira等[8]使用自适应神经模糊推理系统作为飞行动力学辨识器和遗传算法在模拟环境中搜索姿态控制的最佳参数,建立使用人工智能技术的新自适应方法.Swarnkar等[9]为解决空气动力学系数在大多数飞行条件下无法准确获得的问题,提出一种采用自适应方法学习和控制未知动力学的反推技术用于飞机的横向控制.
针对具有强耦合性和强非线性特征的无人机在全包线飞行过程中气动参数摄动大、不确定性强、扰动未知等问题,提出一种新型的增益自适应超螺旋滑模(ASTSM)姿态控制算法.创新之处在于:首先,针对多变量的二阶无人机系统模型,通过引入自适应项,使ASTSM控制器增益能够达到非高估的最佳值,抑制了控制器的抖振;其次,所提出的ASTSM控制算法在有界且变化率有界的扰动上界未知的情况下,能够有效抑制扰动.
1 无人机数学模型
无人机的姿态变化涉及惯性坐标系Oexeyeze和机体坐标系Obxbybzb等,无人机在坐标系中的示意图如图1所示.图中:p为滚转角速度;q为偏航角速度;r为俯仰角速度.
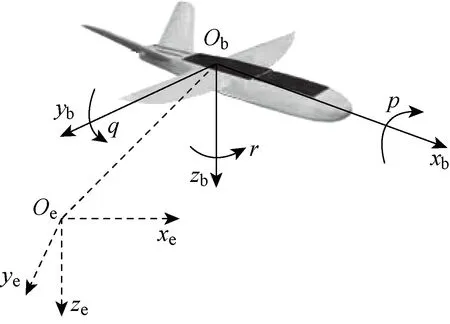
图1 无人机坐标示意图Fig.1 Diagram of referential frames configuration of UAV
该类型无人机的姿态运动方程[10]如下:
(1)
式中:θ为俯仰角;φ为偏航角;γ为滚转角;Jx为绕x轴的转动惯量;Jy为绕y轴的转动惯量;Jz为绕z轴的转动惯量;Ma为滚转力矩;Me为俯仰力矩;Mr为偏航力矩.
令无人机的合力矩为M=[MaMeMr]T,主要分为飞行过程中的气动力矩和舵面偏转产生的操纵力矩.
假设无人机为刚体,其旋转运动主要考虑姿态角Ω=[θφγ]T和姿态角速度ω=[pqr]T这6个变量的变化规律,将动力学微分方程改写为
(2)
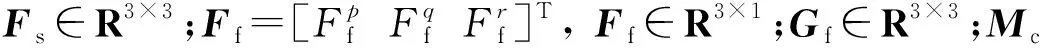
Laero=qaSLlaero
Maero=qaSLmaero
Naero=qaSBanaero
Mc=[LcMcNc]T
其中:Laero,Maero,Naero分别为滚转、偏航、俯仰通道的气动力矩,令Maero=[LaeroMaeroNaero]T为气动力矩;qa为动压;S为机翼参考面积;L为机翼长度;Ba为平均气动弦长;laero为滚转通道上的气动力矩系数;maero为偏航通道上的气动力矩系数;naero为俯仰通道上的气动力矩系数,可以通过无人机飞行过程中的迎角(α)和马赫数(Ma)变化拟合得到,naero和laero变化如图2和图3所示;Lc为滚转通道上的控制力矩;Mc为偏航通道上的控制力矩;Nc为俯仰通道上的控制力矩.

图2 气动俯仰力矩系数Fig.2 Aerodynamic pitching moment coefficient
Mc与无人机舵面的映射关系表示如下:
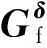

图3 气动滚转力矩系数Fig.3 Aerodynamic rolling moment coefficient
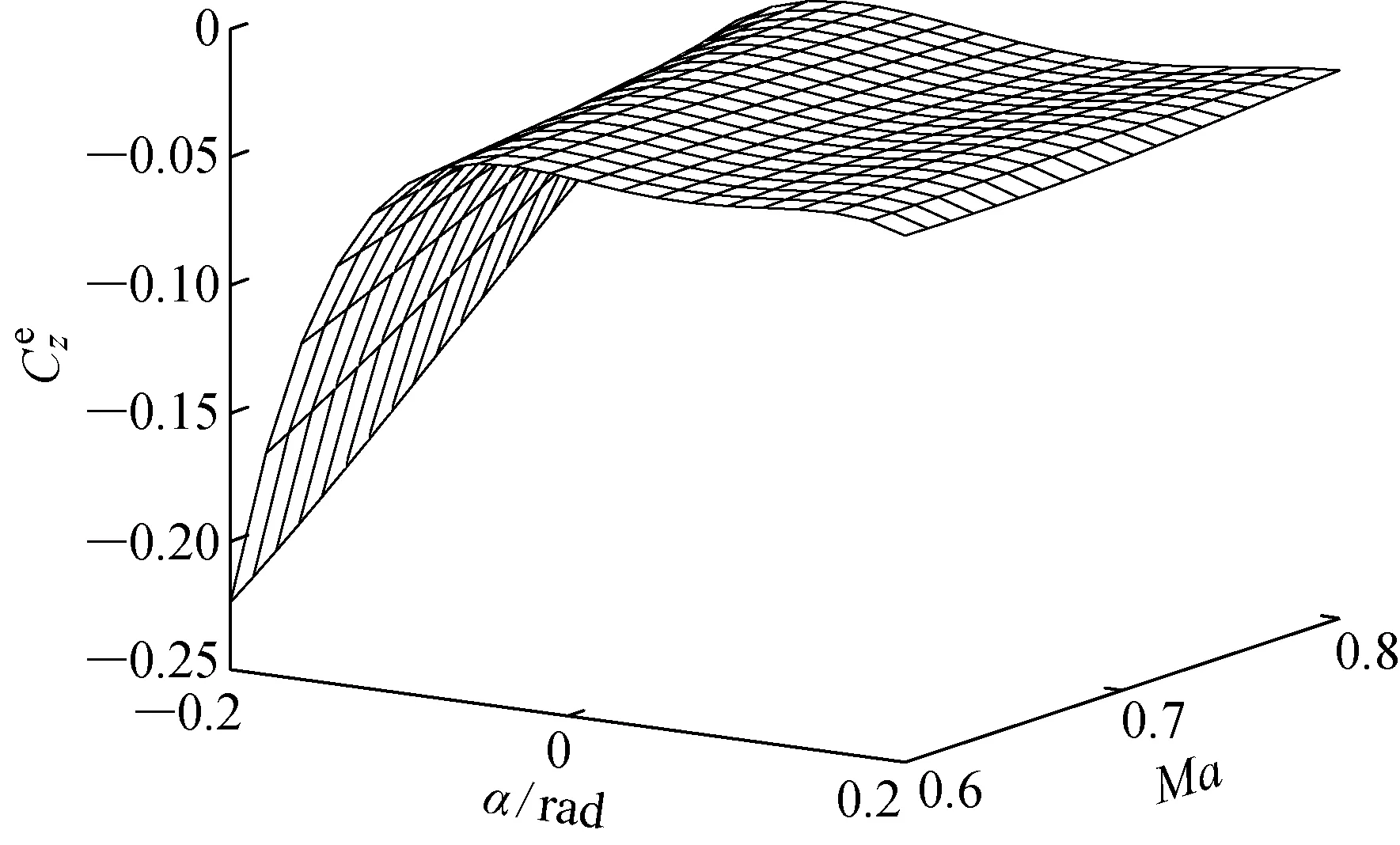
图4 操纵俯仰力矩系数Fig.4 Control pitching moment coefficient
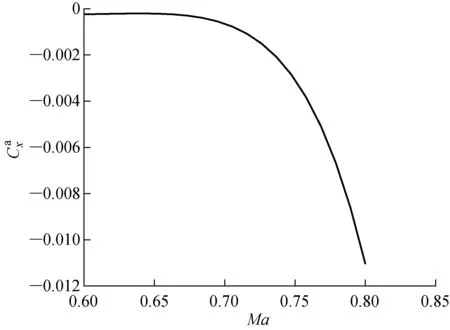
图5 操纵滚转力矩系数Fig.5 Control roll moment coefficient
由图2~5可知,无人机全包线飞行过程中,在不同迎角和马赫数的情况下气动参数摄动变化明显,具有很强的不确定性.
2 基于ASTSM算法的控制器设计
滑模算法及其改进算法被广泛应用于各种复杂的非线性系统控制中[11-12].针对式(2)所示的模型,提出一种基于ASTSM算法的控制器,来跟踪无人机的给定姿态角Ωd.如图6所示,自适应机制可以根据姿态角误差e调节控制器增益k1的值,主要用来提供非高估的控制器增益,以减少干扰未知时过大的控制器增益可能带来的抖振;sat(·)为饱和函数.控制器基于超螺旋算法的滑模控制实现无人机姿态角跟踪控制.
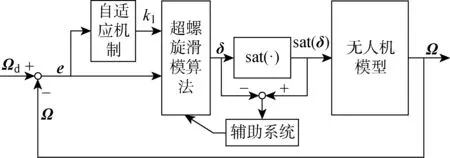
图6 无人机姿态控制框图Fig.6 UAV attitude control diagram
定义姿态角的跟踪误差为
e=Ω-Ωd
(3)
式中:e∈R3×1;Ωd∈R3×1为目标姿态角,对式(3)求导有
(4)

(5)
考虑舵面偏转存在饱和的情况和外部干扰对系统产生的扰动力矩Md=[LdMdNd]T,其中Ld,Md,Nd分别为滚转、偏航、俯仰通道上的扰动力矩,将式(5)转化为如下形式:
(6)
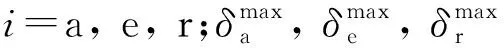
(7)

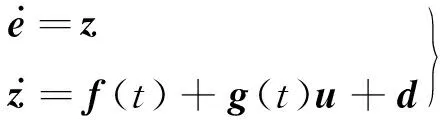
(8)
式中:f(t)∈R3×1;g(t)∈R3×3;t为时间;d∈R3×1;u∈R3×1,表达式为
(9)
针对系统模型式(8), 做出如下假设.

设计滑模面如下:
(10)
式中:s∈R3×1;c1∈R3×3,c1=diag(c11,c12,c13)为待设计的Hurwitz矩阵.易知所设计的滑模面可以使得姿态角误差和姿态角误差变化率以指数形式快速收敛,对滑模面s求导可得:
(11)
采用文献[14]中设计的超螺旋滑模控算法并结合本文二阶系统式(8),可以得到控制器表达式如下:
(12)
式中:k1>0;k2>0为待设计的控制器参数.将式(12)带入式(11)中可以得到如下表达式,即
(13)
令ξ=[ξ1ξ2]T,且:
(14)
对式(14)进行求导得到:
(15)
将式(14)带入式(15)中得到:
(16)
设计如下控制器的增益自适应律:
(17)
式中:αc,β,ε,ν为大于0的常数.
引理1[15]对于非线性系统,假设存在连续可微的正向无界函数V(x):Rm→R+和常数κ>0,0<λ<1,0<η<∞满足下列条件,即
(1)V(x)=0⟹x=0
则系统可以在有限时间内收敛,收敛时间为
其中:θ0为影响收敛时间的参数.
定理1对于二阶系统模型式(8),设计滑模面式(10)、超螺旋算法式(12)和控制器增益自适应律式(17),选取适当的控制器参数变量αc,β,ε,ν,式(8)将在有限时间收敛.
证明选择如下Lyapunov候选函数,即
(18)
(19)
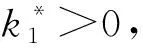
(20)
(21)

对于正定矩阵P和Q,有如下不等式关系:
(22)
式中:λmin{·}为矩阵最小特征值;λmax{·}为矩阵最大特征值.
根据式(14)可得:
(23)
将式(22)和式(23)带入式(20)可得:
(24)
对式(18)求导可得:

(25)
根据文献[16]中的不等式:
(26)
m≤n
结合式(25)和式(26)可得:
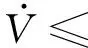
(27)
式(27)满足引理1条件,因此ξ1和ξ2能够在有限时间收敛,同时滑模面s也在有限时间内收敛.
3 仿真与分析
以本文中无人机的气动数据和转动惯量为例,其转动惯量为

给定姿态角初始值Ω0=[0.573 0.573 0.573]T,目标姿态角Ωd=[5.735.735.73]T,姿态角速率初始值ω0=[000]T,滑模面参数c1=diag(2, 2, 2),自适应律参数ε=0.003,αc=6,β=4,k1的初始值为20.
本文设计的ASTSM算法的增益k1变化如图7所示.由图可知,在t=2 s左右,系统的姿态角误差e收敛至收敛域‖e‖<ε中,此时控制器增益k1停止变化,达到非高估的最佳值.
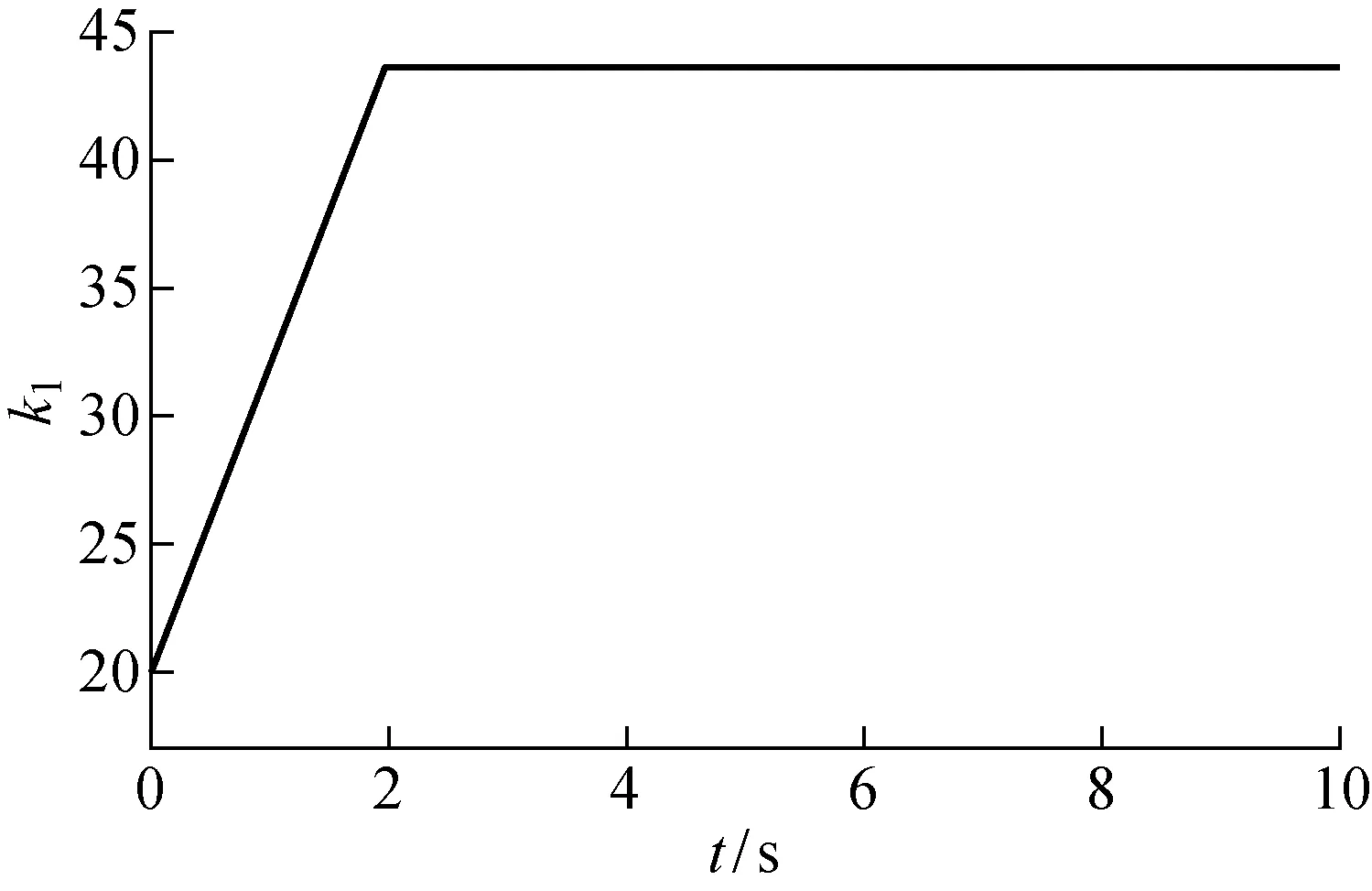
图7 控制器增益变化曲线Fig.7 Changing curve of adaptive-gain of controller
图8和图9分别为本文设计的ASTSM控制器和普通滑模(SM)控制器的姿态角误差变化曲线.e=[eθeφeγ],其中eθ,eφ,eγ分别为俯仰角误差、偏航角误差和滚转角误差.对比图8(a)与图9(a)以及图8(b)与图9(b)可知,在6.1 s附近,ASTSM控制器使无人机姿态角误差收敛到原点附近的极小领域,相较于SM控制器作用下姿态角误差收敛到的领域更小.因此,ASTSM控制器能够使被控对象更快收敛.

图8 ASTSM姿态角误差变化曲线Fig.8 Error curves of attitude angle by ASTSM

图9 SM姿态角误差变化曲线Fig.9 Errors curves of attitude angle by ASTSM
图10~ 12为本文设计的ASTSM控制器、SM和PID控制器的无人机姿态角跟踪曲线对比.对比图10~12可知,无人机系统非线性强,普通PID控制难以满足要求,控制品质较差,出现较大超调,并且收敛时间长.对比图8~12可知,本文设计的控制器能够满足无人机系统非线性控制要求,并且引入自适应项,使控制器具有非高估的最佳增益,因此相较于普通滑模控制具有更快的收敛速度.
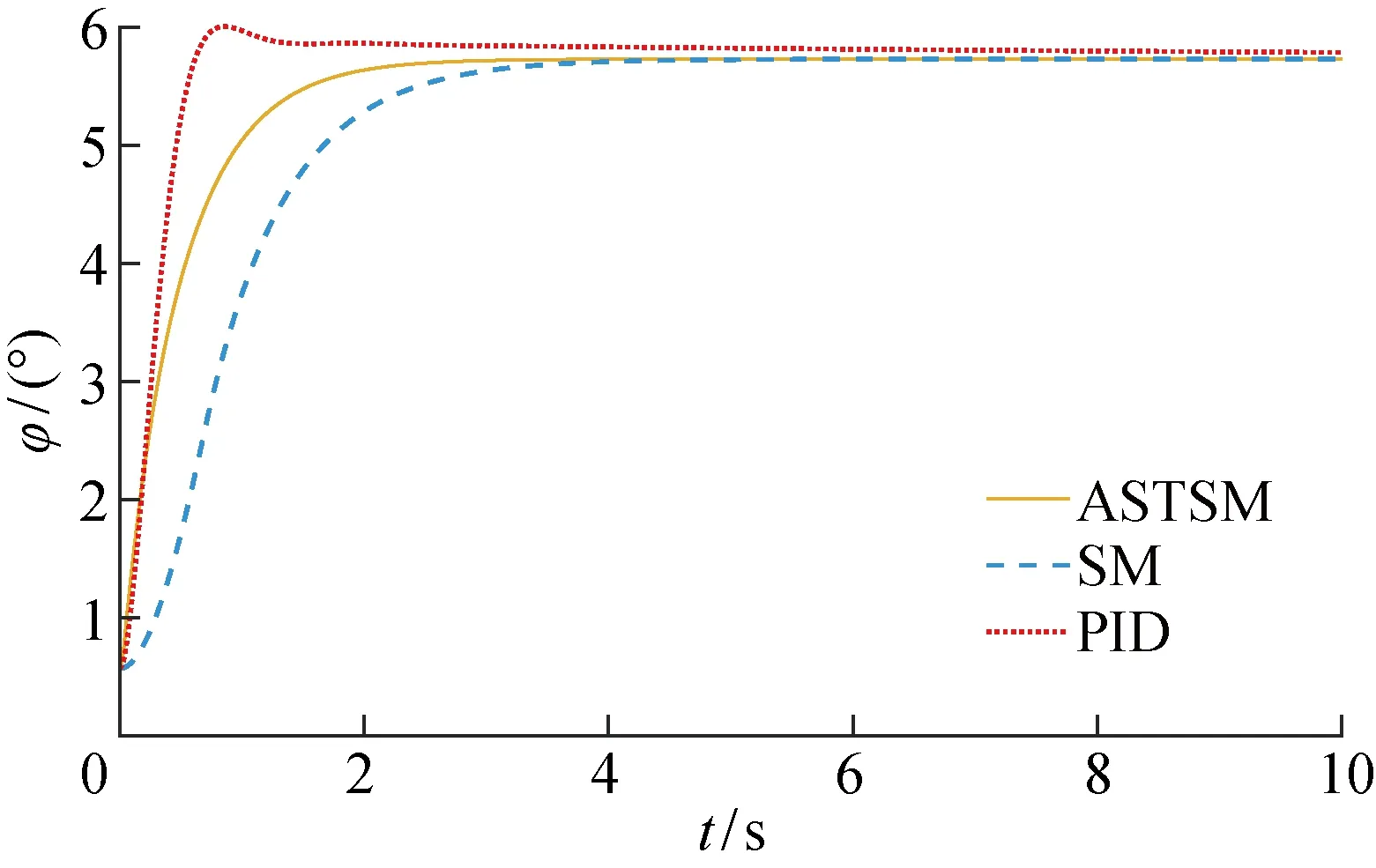
图10 偏航角跟踪曲线Fig.10 Tracking curves of yaw angles

图11 俯仰角跟踪曲线Fig.11 Tracking curves of pitch angles
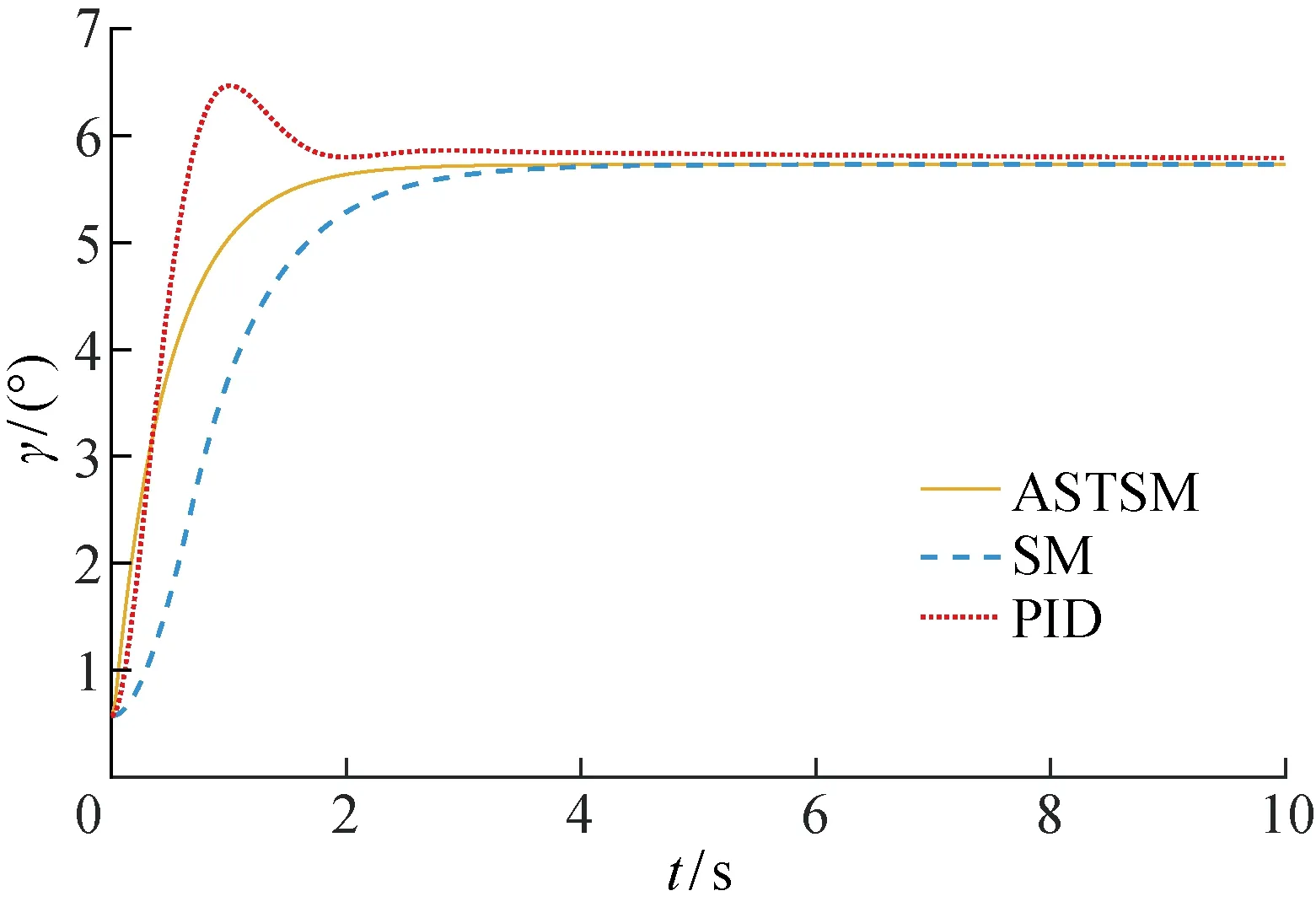
图12 滚转角曲线Fig.12 Tracking curves of roll angles
仿真时加入d=[0.2sint0.15sint0.1sint]T的扰动,得到本文设计的ASTSM控制器、SM和PID控制器的无人机姿态角跟踪曲线图,如图13~15所示.对比图13~15可知,无人机全包线飞行过程中,气动参数摄动大,外部扰动等不确定性强,普通PID控制难以抑制扰动,无法满足无人机姿态控制要求.本文设计的ASTSM控制器能够有效抑制外界干扰,满足无人机全包线飞行要求.

图14 俯仰角跟踪曲线(扰动)Fig.14 Tracking curves of pitch angles with disturbance
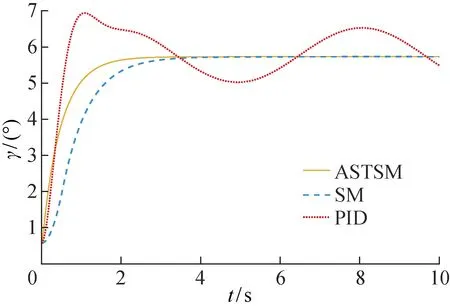
图15 滚转角曲线(扰动)Fig.15 Tracking curves of roll angles with disturbance
4 结语
基于增益自适应超螺旋滑模控制算法设计的无人机姿态控制器ASTSM能够有效解决无人机在全包线飞行过程中遇到的气动参数摄动大、非线性强、扰动干扰强等问题.理论分析表明,该控制器能够有效适用于无人机的姿态跟踪要求.

