高超声速飞行器线性变参数一体化式控制律设计

杨 庶， 钱云霄， 杨 婷,2

(1. 西北工业大学 自动化学院，西安 710072； 2. 北京空天技术研究所，北京 100074)

高超声速飞行器可进行跨空域、跨速域飞行，其复杂的飞行环境和时变的飞行动态给控制系统的设计带来严峻挑战.针对上述问题，目前常采用动态逆控制、反演控制、滑模控制、切换控制、自适应控制、线性变参数(LPV)控制等方法进行控制器设计.文献[1]针对制导控制一体化问题，提出一种基于鲁棒动态逆的动态面一体化算法，通过引入动态面控制，避免反演控制的“计算膨胀”问题.文献[2]设计了一种无需在线求导的高超声速飞行器反步法控制律方法，用于实现高超声速飞行器纵向通道的航迹倾斜角跟踪控制.模型的强非线性和强耦合性特点使得动态逆、反步法等控制器设计过程复杂，增加了实际应用难度[1,3].对于高超声速飞行器纵向控制通道的速度和高度控制问题，文献[4]设计干扰补偿器和状态反馈控制律，在实现指令跟踪的同时，提高飞行器闭环系统相对于外界扰动的鲁棒性.文献[5]给出一种基于模糊控制理论的高超声速飞行器纵向最优控制律，能够在飞行器未建模动力学特性的影响下，实现对飞行器高度和速度指令的跟踪.文献[6]采用有限时间滑模控制理论，设计高超声速飞行器在俯冲段的协同制导律，实现多枚高超声速飞行器攻击同一固定目标的控制任务.文献[7-8]分别采用滑模和自适应控制理论实现高超声速飞行器俯冲段的控制.文献[9]针对吸气式高超声速飞行器的纵向飞行控制，建立多胞刚性LPV模型，进而基于区域极点配置实现系统的H∞/H2多目标鲁棒控制.文献[10]将切换控制思想与LPV控制结合，通过减小子系统的参数变化范围，增强系统的鲁棒性.

上述控制方法中，LPV控制利用参数依赖的思想，既可以有效适应高超声速飞行器飞行包线大、参数快时变的特点，又可以基于增益调度技术保证闭环系统的稳定性和控制器的实用性，在高超声速飞行器控制中得到广泛应用.需要指出的是，现有的飞行器LPV控制研究一般仅考虑飞行器纵向或横航向动力学特性[11-12]，忽略纵向和横航向通道之间的耦合.基于飞行器完整模型的LPV控制研究通常引入模型假设(如速度倾侧角为0)，降低控制律的设计难度.

本文基于高度-水平航迹控制概念，将高超声速飞行器三维航迹分解为竖直面航迹和水平面航迹，通过高度、速度、侧滑角、偏航角控制，实现飞行器的三维航迹控制.基于高度-水平航迹控制概念，采用具有L2诱导范数控制性能的LPV控制方法，设计高超声速飞行器的一体化式LPV控制律.在地心地固(ECEF)参考系下建立高超声速飞行器的数学模型，通过数值仿真检验一体化式LPV控制律在测量噪声影响下的控制性能.仿真结果表明，该控制律能够跟踪给定控制指令，并具有较好的噪声抑制性能.

1 高超声速飞行器数学模型

基于WGS84地球模型参数，在ECEF参考系(见图1)下建立飞行器的非线性数学模型，在模型中考虑地球自转、地球扁率、地球引力二阶简谐效应的影响.图中：l和μ为大地经度和大地纬度；ωE为地球自转速度；lE为地球自转角；ECI代表地心惯性参考系；B代表机体参考系.为便于控制律设计，基于平板地球假设，建立飞行器的简化非线性数学模型，进而得到高超声速飞行器的LPV模型.在两组数学模型中均假设飞行器为刚体，并忽略飞行器的质量变化.

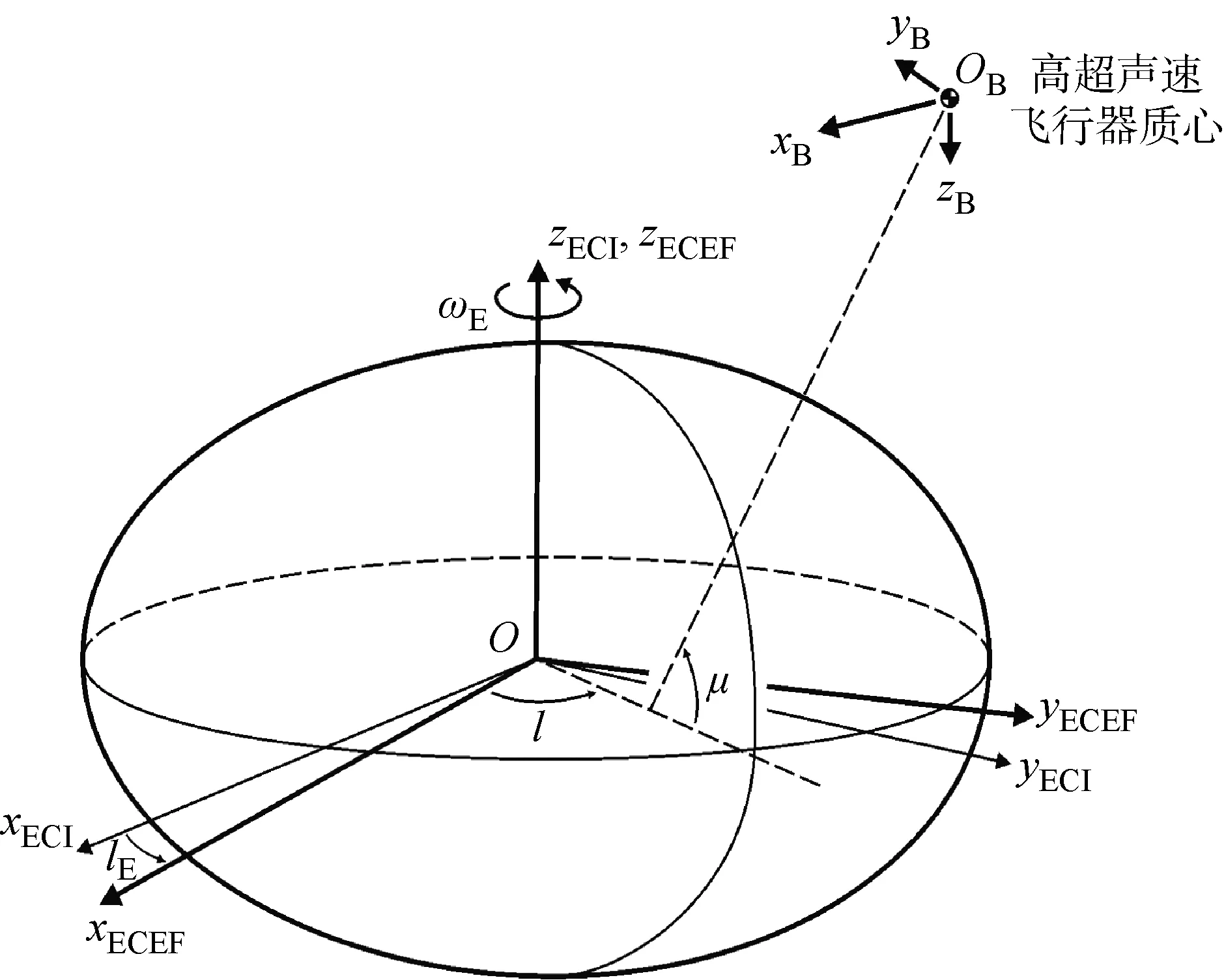
图1 ECEF参考系与机体参考系示意图Fig.1 ECEF reference frame and body reference frame

1.1 ECEF参考系下的运动方程

由于地球自转的影响，图1所示的ECEF参考系是相对于ECI参考系的非惯性参考系，其角速率向量为

(1)

(2)

在ECEF参考系中，高超声速飞行器的平动运动受到地球自转角速度、Coriolis效应、地球扁率等因素影响，根据牛顿第二定律，在机体参考下可将高超声速飞行器的平动动力学方程表达为

(3)

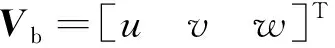
ge=

(4)

式中：GM为地心引力常数；J2为地球引力二阶简谐效应常数；a为地球半长轴；μc为地心纬度；rk(k=1,2,3)为飞行器位移向量r的第k个分量；‖r‖为飞行器相对于地心的距离.GM，J2，a均根据WGS84地球模型参数确定，式(3)和(4)的详细推导过程参见文献[13].

根据文献[14]中的气动参数进行计算，有

Fb=

(5)

式中：α为迎角；T为发动机推力，可通过燃油流量比δt进行控制；D，L和Y为飞行器的阻力、升力和侧力，可分别通过副翼舵偏角δa、升降舵舵偏角δe和方向舵舵偏角δr进行控制.

高超声速飞行器的转动动力学方程为

(6)

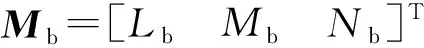
ωb=ωbn+Rbnωne+Rbeωe

(7)

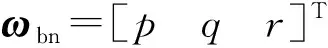
(8)

高超声速飞行器的位移和四元数姿态运动学方程为

(9)

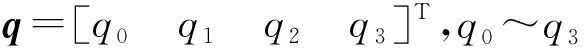
1.2 平板地球假设下的运动方程和LPV模型

为便于控制律设计，可忽略地球自转和引力二阶简谐效应，根据式(3)、式(6)和式(9)进行简化，在平板地球假设下建立高超声速飞行器的简化运动方程[13]，即

(10)

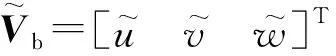
根据基于线性化的LPV模型建模方法[16]，可将式(10)转化为如下高超声速飞行器LPV模型，即

(11)

2 一体化式LPV控制律

针对高超声速飞行器的三维航迹控制需求，基于高度-水平航迹控制概念设计高超声速飞行器一体化式LPV控制律，进而采用线性矩阵不等式(LMI)方法求解该LPV输出反馈控制律的参数.

2.1 高度-水平航迹控制概念

根据笛卡尔参考系中基向量相互正交的性质，可根据北东地参考系，将高超声速飞行器的三维航迹控制问题分解为水平面和竖直面航迹控制问题(见图2).竖直面航迹控制可通过高度控制实现，水平面航迹控制问题可通过速度和偏航角控制实现.由于高超声速飞行器通常要求实现协调转弯性能，即水平面航迹控制时侧滑角为0°，所以侧滑角控制应作为水平面航迹控制目标之一.

根据上述讨论，控制指令可选：速度V、侧滑角β、高度h、偏航角ψ.由于这些控制指令既包含常规飞行控制的内回路姿态控制指令，也包含外回路控制指令，所以通常需要进行内外回路控制律的分离设计与综合，进而实现飞行器三维航迹控制.由于内外回路控制律分离设计方法有可能导致控制律之间的耦合问题，所以本文采用LPV输出反馈控制理论，设计高超声速飞行器一体化式LPV飞行控制律，使用LMI方法求解具有L2诱导范数性能的LPV鲁棒控制律参数.

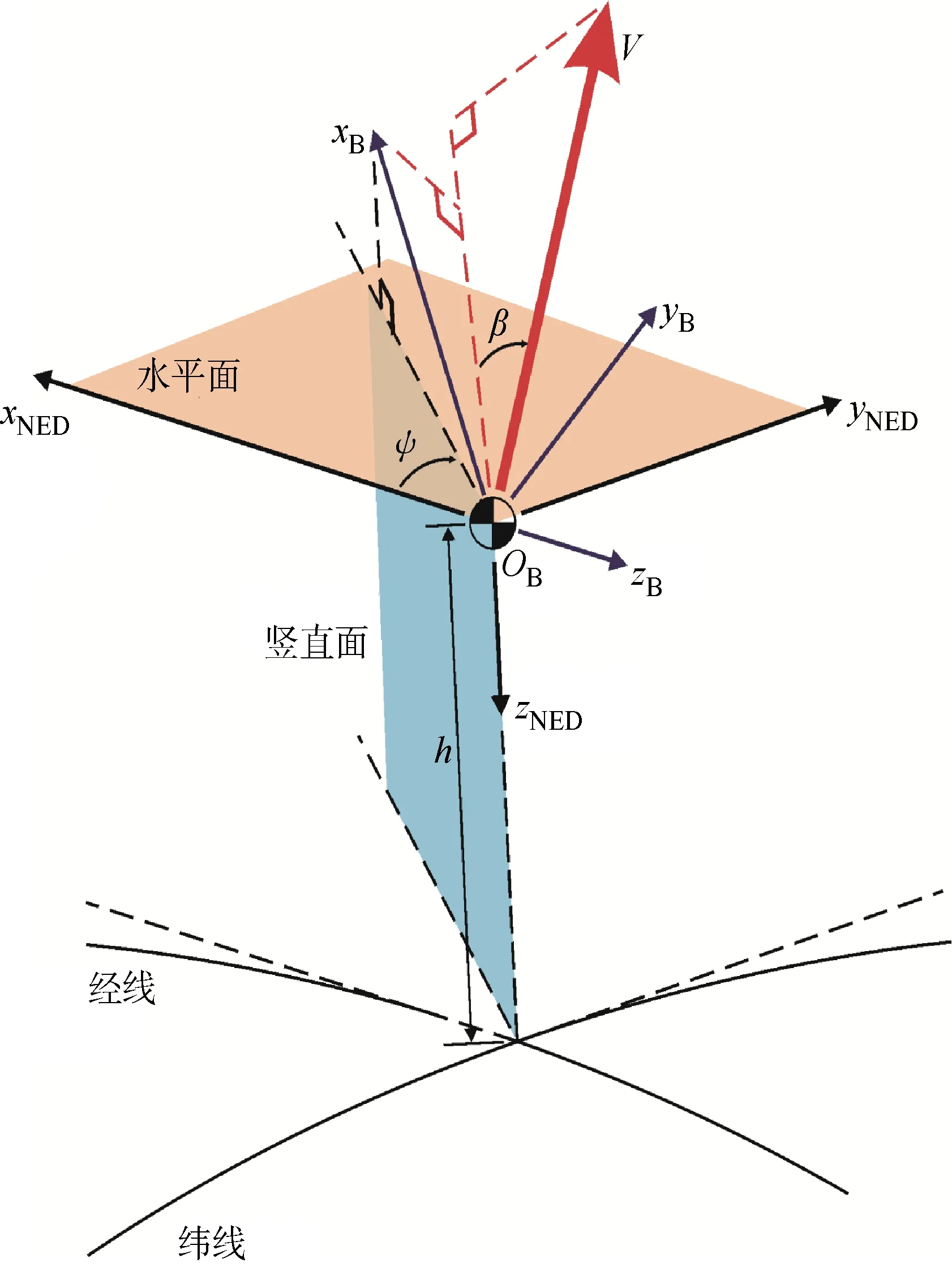
图2 高度-水平航迹控制概念示意图Fig.2 Altitude-horizontal trajectory control concept

2.2 LPV控制律设计

高超声速飞行器一体化式LPV控制律如图3所示，通过参考模型和L2诱导范数意义下的模型匹配方法[17]，实现速度、侧滑角、高度、偏航角通道的模型跟踪控制性能.图中：下标c代表控制指令；向量n为反馈噪声.各控制通道的参考模型均为阻尼比0.7的二阶系统，则有传递函数：

(12)

式中：s为传递函数的复频域自变量.

误差权值函数设计为

(13)

式中：WV(s)和Wh(s)的低频增益为0.01，设计目标为使速度和高度的稳态控制误差不超过1%；Wβ(s)和Wψ(s)的低频增益为0.001，设计目标为使侧滑角和偏航角的稳态控制误差不超过0.1%.

控制权值函数设计为

(14)

其设计目标为在单位指令信号的作用下，高超声速飞行器燃油流量的变化量不超过20%，副翼、升降舵、方向舵的变化量不超过10°.式(13)和式(14)中各权值函数的输出分别对应于图3中的eV、eβ、eh、eψ和eu.

反馈信号设计为

xf=

(15)

各反馈信号均受测量噪声影响.

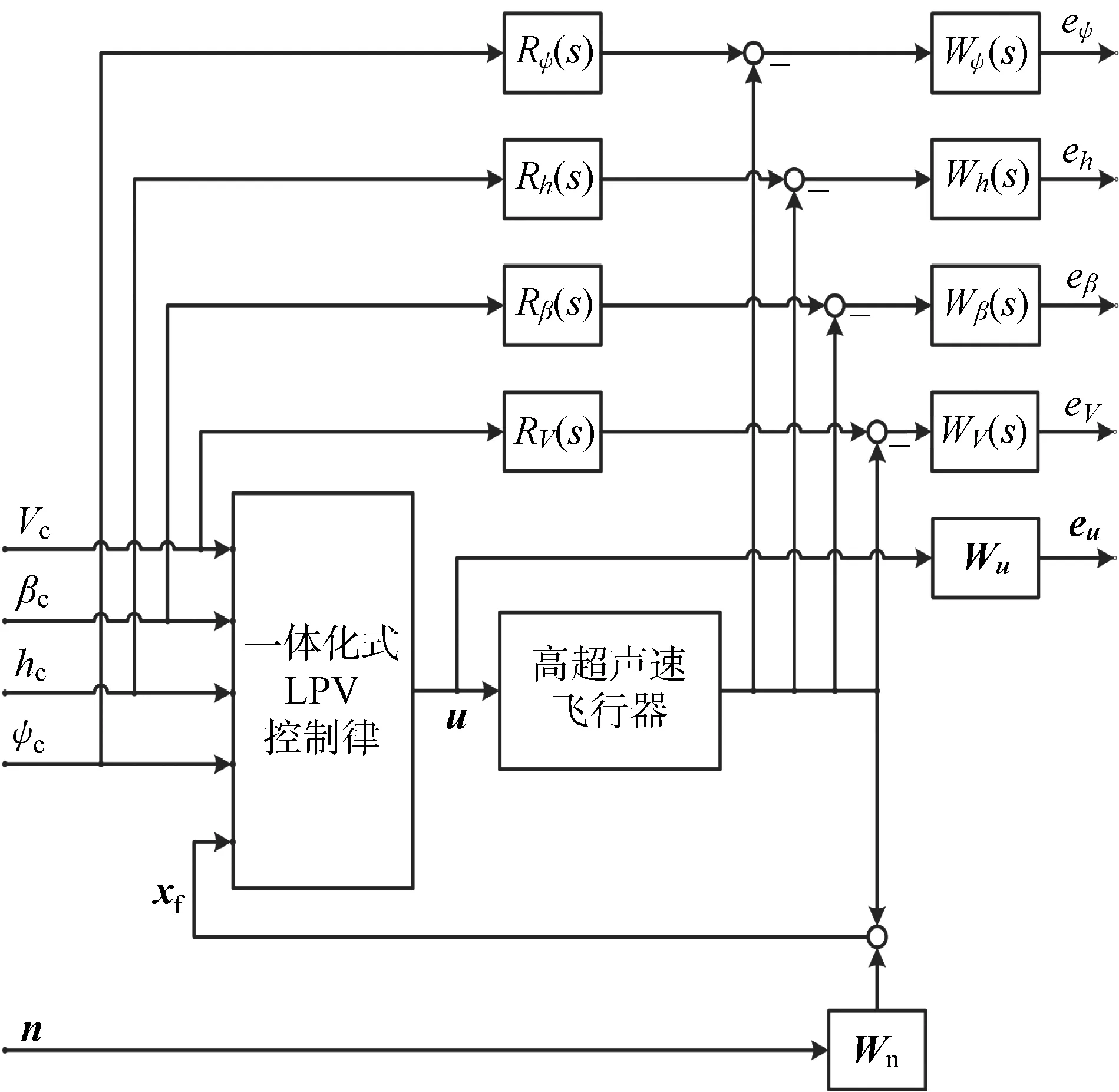
图3 LPV控制律与系统连接结构Fig.3 System interconnections for LPV control law

噪声权值函数设计为

Wn=

(16)

式中：I3和I6分别为三维单位矩阵和六维单位矩阵.式(16)代表速度、位移、角度和角速率反馈信号的噪声幅值分别不超过0.01 m/s、0.01 m、0.01° 和 1.75×10-4rad/s.

根据式(11)～(16)，用于控制律设计的LPV模型可表达为

(17)

式中：xL为状态变量，包括式(11)～(13)的状态变量；d为广义输入，包括控制指令和测量噪声；e为广义误差，由式(13)的输出信号给定；y为输出信号，由控制指令和反馈信号给定.对于式(17)中的线性系统，A为系统状态矩阵，B1为广义输入的输入矩阵，B2为控制输入的输入矩阵，C1为广义误差的输出矩阵，C2为输出信号的输出矩阵，D11为从广义输入到广义误差的前馈矩阵，D12为从控制输入到广义误差的前馈矩阵，D21为从广义输入到输出信号的前馈矩阵.

控制律在马赫数包线内进行设计，所采用的马赫数包线为4≤Ma≤6.为保证LMI的约束条件为有限维，采用如下的包线离散网格进行控制律参数求解：

P=

{4, 4.25, 4.5, 4.75, 5, 5.25, 5.5, 5.75, 6}

(18)

LPV控制器参数通过求解如下的LMI进行确定[18]，即

(19)

(20)

式(19)中的LMI使闭环系统具有D-稳定性[18-19]，并且保证闭环系统满足如下的L2诱导范数性能，即输入-输出L2稳定性:

(21)

LPV控制律可表达为

(22)

控制律的参数可通过下式计算：

(23)

式中：矩阵N为中间变量.式(23)的具体推导过程参见文献[18].式(19)中的待求矩阵采用如下的参数化格式，即

(24)

式中：0, 1, 2代表阶次；ρ定义为ρ=(Ma-4)/2.矩阵R(ρ)表达为马赫数的二次方程形式，使控制律能够对高超声速飞行器在不同飞行速度下的运动特性非线性变化进行有效控制.其余待求矩阵均设为常数矩阵，降低控制律求解和实现所需计算量.

3 仿真结果

基于高超声速飞行器平板地球假设下的运动方程，分析飞行器开环系统和闭环系统的稳定性.采用ECEF参考系下的高超声速飞行器运动方程，通过竖直面机动和水平面机动的数值仿真，检验一体化式LPV控制律的控制性能和鲁棒性.

3.1 稳定性分析

根据平板地球假设下的运动方程，高超声速飞行器在马赫数包线4≤Ma≤6中的极点分布如图4所示.图中：zb为飞行器的极点；ωn和ξ分别为飞行器极点的自然频率和阻尼比.由图可见，飞行器是开环不稳定系统，不稳定极点的最高自然频率接近于10 rad/s，说明该飞行器的开环不稳定性较高，而本文设计的一体化式LPV控制律能够保证闭环系统为稳定系统，并且所有极点在复平面上均分布在阻尼比大于0.5、自然频率小于30 rad/s的扇形区域内，实现式(19)给定的闭环系统D-稳定性要求.同时，闭环系统的大多数极点的阻尼比大于0.7，说明一体化式LPV控制律能够为高超声速飞行器闭环系统提供良好的阻尼特性.

图4 高超声速飞行器开环和闭环系统极点分布Fig.4 Open-loop and closed-loop poles of a hypersonic vehicle

3.2 跃升加速机动

采用ECEF参考系下的高超声速飞行器运动方程进行数值仿真，使飞行器在竖直面内进行高度跃升和水平加速机动，检验基于飞行器简化模型设计的LPV控制律在地球自转、地球扁率、地球引力二阶简谐效应等扰动下的控制性能.仿真中，在反馈信号中增加测量噪声，检验该控制律相对于噪声的鲁棒性.速度、位移、角度和角速率反馈信号的噪声幅值分别设置为0.005 m/s、0.005 m、0.005°和8.726×10-5rad/s.

如图5所示，一体化式LPV控制律能够使高超声速飞行器跟踪给定的高度和速度指令，机动过程中侧滑角和偏航角没有出现明显的控制误差.同时，测量噪声对飞行器闭环系统控制性能的影响很小，没有出现控制性能恶化的现象.图中：t为时间.从图6和图7所示的高超声速飞行器在ECEF参考系下的状态变量响应可以看出，高超声速飞行器具有闭环稳定性，说明该控制律在地球自转、地球扁率、地球引力二阶简谐效应等扰动和测量噪声的影响下仍具有良好的控制性能和鲁棒性.

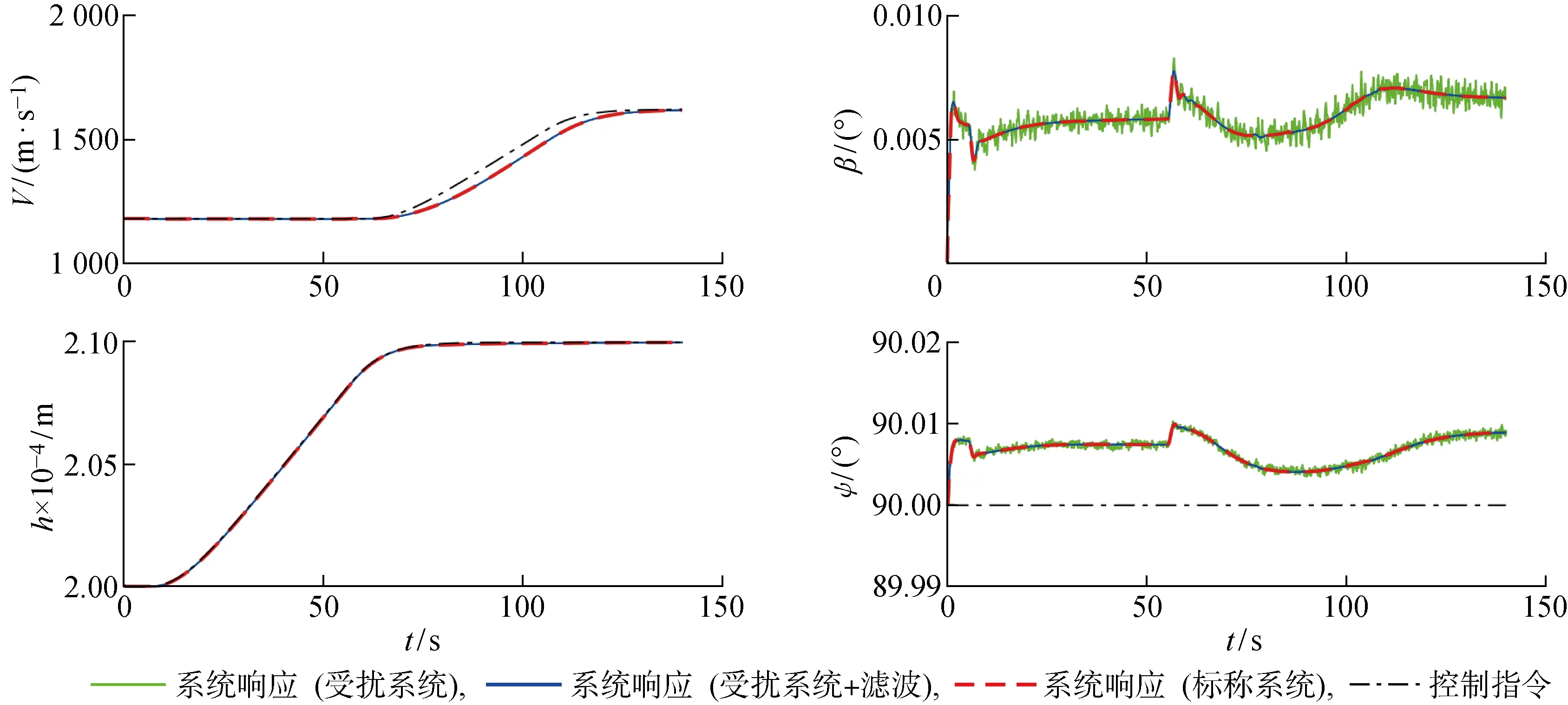
图5 控制指令与系统响应(跃升加速机动)Fig.5 Control commands and system responses (ascent-acceleration maneuver)

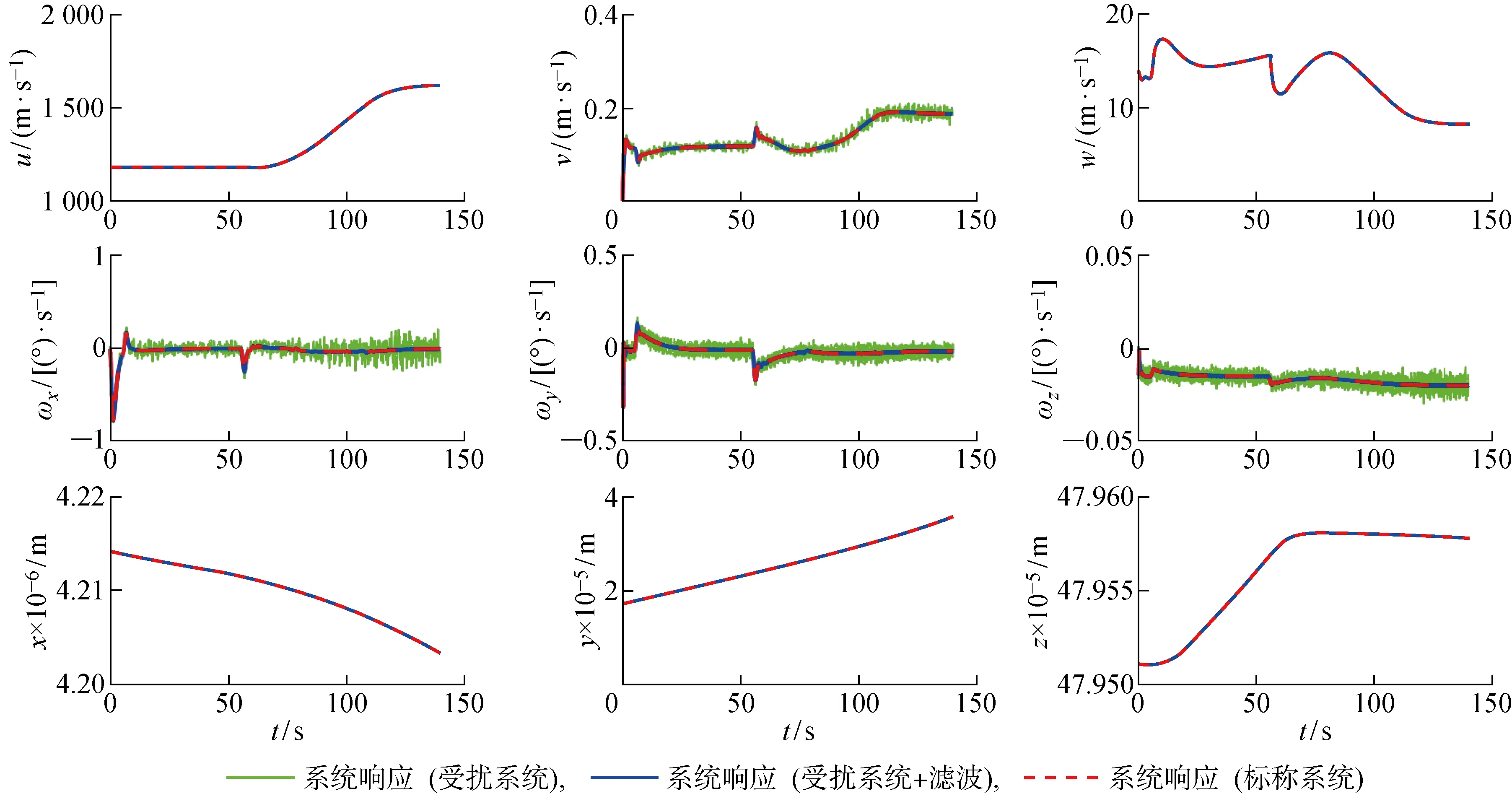
图6 ECEF参考系下高超声速飞行器运动方程的状态响应(跃升加速机动)Fig.6 State responses of hypersonic vehicle equations of motion in ECEF reference frame (ascent-acceleration maneuver)

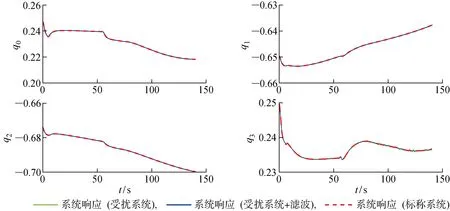
图7 ECEF参考系下高超声速飞行器的姿态四元数响应(跃升加速机动)Fig.7 Quaternion responses of hypersonic vehicle equations of motion in ECEF reference frame (ascent-acceleration maneuver)

从图8所示的控制输入可以看出，在标称条件下高超声速飞行器完成跃升加速机动所需的控制输入量较小.但在测量噪声的影响下，LPV控制律输出的控制输入中包含较为明显的噪声，不利于实际应用.为消除该噪声影响，在LPV控制律的反馈信号中增加二阶低通滤波器：

(25)

式中：滤波器自然频率ωf=40 rad/s；阻尼比ξf=1.

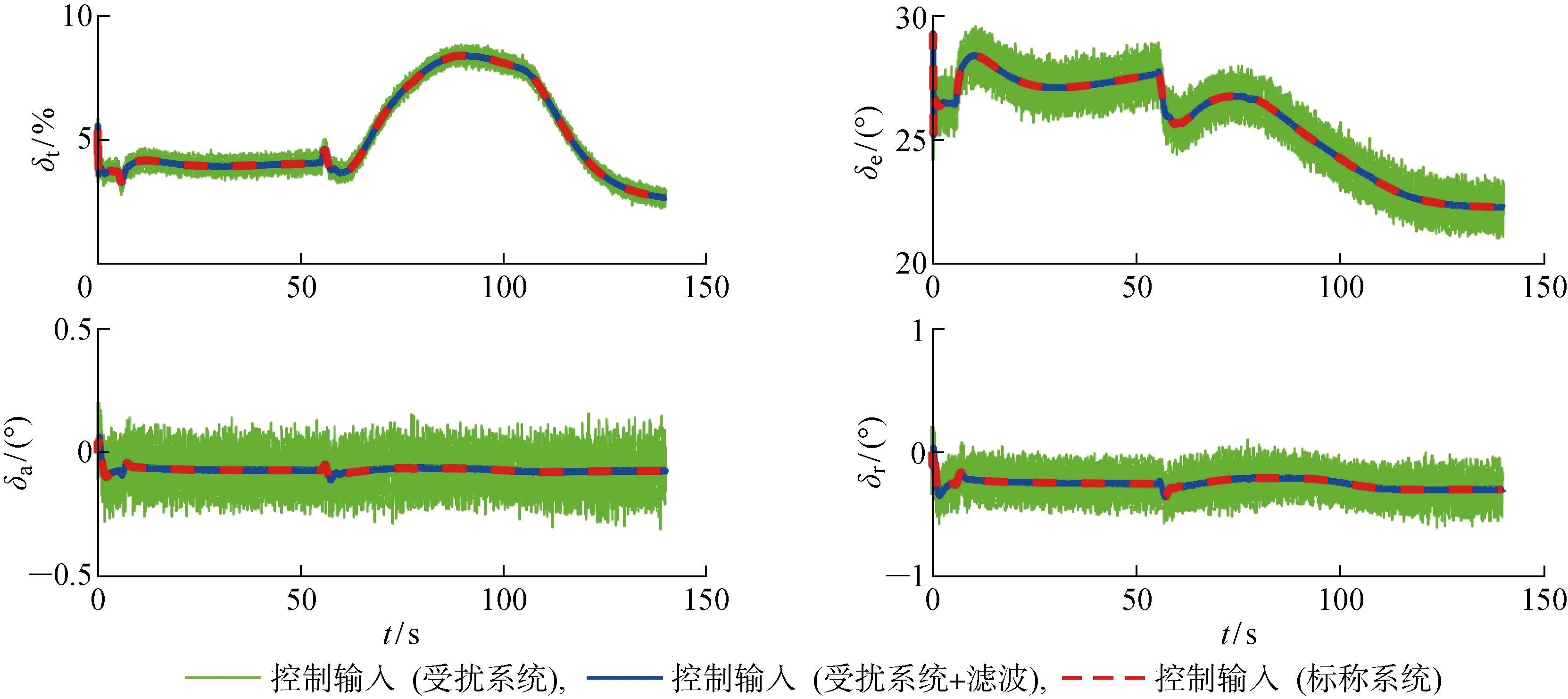
图8 控制输入(跃升加速机动)Fig.8 Control inputs (ascent-acceleration maneuver)

从图5～7的仿真曲线中可以看出，对反馈信号进行滤波后，高超声速飞行器闭环系统在测量噪声的影响下仍然具有良好的响应特性，并且LPV控制律生成的控制输入得到明显的降噪和平滑化.

3.3 水平转弯机动

采用ECEF参考系下的高超声速飞行器运动方程进行数值仿真，使飞行器在水平面内进行水平转弯机动.仿真中，在反馈信号中增加测量噪声，噪声幅值设置与3.2节相同.

从图9可以看出，一体化式LPV控制律能够使高超声速飞行器跟踪给定的偏航角指令，使飞行器完成45°的水平转弯机动，机动过程中侧滑角的控制误差小于0.2°，说明飞行器实现了协调转弯控制性能.同时，测量噪声对飞行器闭环系统的控制性能影响很小，没有出现控制性能恶化的现象.

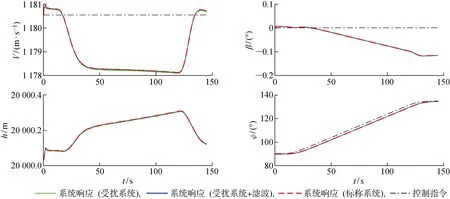
图9 控制指令与系统响应(水平转弯机动)Fig.9 Control commands and system responses (level turn maneuver)

从图10和图11所示的高超声速飞行器在ECEF参考系下状态变量响应可以看出，高超声速飞行器具有闭环稳定性，说明该控制律在地球自转、地球扁率、地球引力二阶简谐效应等扰动和测量噪声的影响下仍具有良好的控制性能和鲁棒性.从图12所示的控制输入可以看出， 高超声速飞行器完成水平转弯机动所需的控制输入量较小.

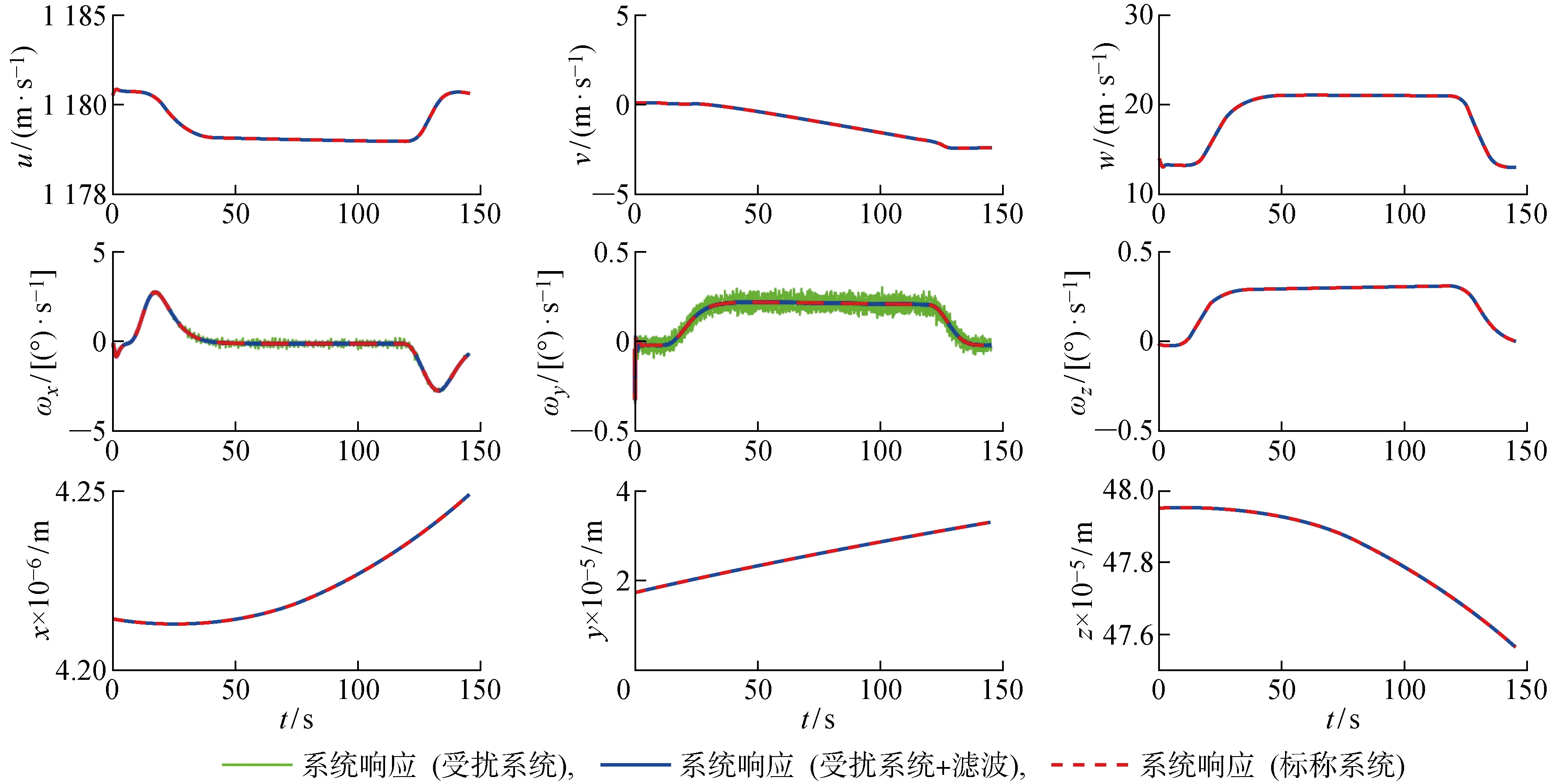
图10 ECEF参考系下高超声速飞行器运动方程的状态响应(水平转弯机动)Fig.10 State responses of hypersonic vehicle equations of motion in ECEF reference frame (level turn maneuver)

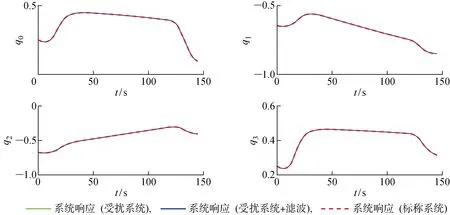
图11 ECEF参考系下高超声速飞行器的姿态四元数响应(水平转弯机动)Fig.11 Quaternion responses of hypersonic vehicle equations of motion in ECEF reference frame (level turn maneuver)

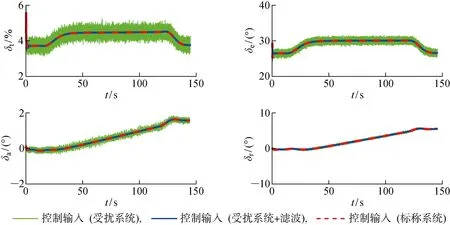
图12 控制输入(水平转弯机动)Fig.12 Control inputs (level turn maneuver)

从图9～12中的仿真曲线可知，在应用式(25)中的二阶低通滤波器对反馈信号进行滤波后，测量噪声对控制输入的影响得到明显的抑制，同时LPV控制律仍能够保持良好的控制性能.

4 结论

针对高超声速飞行器三维航迹控制问题，基于高度-水平航迹控制概念，设计了一体化式LPV控制律.该控制律不区分常规飞行控制的内外控制回路，在L2诱导范数意义下具有良好的控制精度和鲁棒性，具体结论如下：

(1) 高度-水平航迹控制概念基于笛卡尔参考系基向量相互正交的性质，将三维航迹控制问题转化为水平面和竖直面航迹控制问题，等价的控制指令为速度、侧滑角、高度和偏航角.

(2) 一体化式LPV控制律在马赫数包线内进行设计，在4≤Ma≤6包线内使高超声速飞行器闭环系统具有L2诱导范数控制性能，在保证控制指令跟踪精度的同时，实现相对于噪声的鲁棒性.

(3) 基于极点配置和LMI方法设计的一体化式LPV控制律使高超声速飞行器闭环系统的极点具有阻尼比不低于0.5、自然频率不高于30 rad/s的性能.

(4) 采用ECEF参考系下建立的高超声速飞行器运动方程进行数值仿真，一体化式LPV控制律能够在地球自转、地球扁率、地球引力二阶简谐效应等扰动下保持良好的控制性能，并且相对于反馈信号中的测量噪声具有良好的鲁棒性.