解决含定弹簧问题的“一图五点二线”

甘肃 赵强强 李胜江

涉及弹簧的问题通常为综合问题，物体运动过程复杂、涉及知识面广、能力要求高，是许多学生望而生畏的题型。但是这类问题对培养学生的物理核心素养具有重要意义，可以有效完善学生的物理观念，提升学生的科学思维和分析探究能力。现有的研究主要是对涉及弹簧的问题进行了分类讨论，针对不同类型提出了不同的解决办法，缺乏系统性，不利于学生物理思维的培养。弹簧产生弹力时的两个端点都要连接物体，若弹簧某一端点的物体固定不动，则称为定弹簧；若弹簧两端连接的物体能同时运动，则称为动弹簧。本文主要以定弹簧为例，展示“一图五点二线”法解决含定弹簧类问题的策略。

1.构建“一图五点二线”

1.1 一个弹簧形变过程图

弹簧的形变可以沿任意方向，但高中阶段只涉及沿弹簧轴线产生压缩或拉伸形变时的问题，同时高中阶段涉及的弹簧为轻弹簧，即不考虑自身重力的作用，弹簧产生形变的整个变化过程如图1。图中①②③④⑤为弹簧变化过程中的几个特殊位置点，其中①②为压缩状态变化过程，④⑤为拉伸状态变化过程。在弹簧产生形变的过程中，它的起点可以是任何一个点(通常为以上五个点中的某一个)，但变化过程只有两个即从起点向序号数值变大方向变化或向序号数值变小方向变化，且变化一般发生在同一状态(即压缩状态或拉伸状态)，具体如图1所示。

图1 弹簧形变过程图

1.2 五个特殊位置点

弹簧在产生形变的过程中，随着形变量的变化，弹簧和弹簧连接物体的对应物理量也随着改变，而在这个变化过程中弹簧在五个点时对应的各个物理量具有特殊性，总结如表1。为了分析方便，用F外表示物体受到的除弹簧弹力之外的其他力的合力，通常为一恒力、方向与弹簧弹力方向相反；F合表示物体受到的总合力；F、x、k分别表示弹簧产生的弹力、形变量和劲度系数；m、v和a分别表示与弹簧连接物体的质量、速度和加速度；Ep表示弹簧的弹性势能，Ek表示与弹簧连接物体的动能，具体分析如表1。

表1 五个特殊点对应物理量的特点

1.3 两条变化主线

弹簧产生形变时的状态有压缩状态和拉伸状态，每个状态又有两条变化主线，分别为压缩状态的①→②→③和③→②→①过程及拉伸状态的③→④→⑤和⑤→④→③过程，在不同状态时物体所受弹簧弹力F反向。尽管弹簧的起点不同，但变化过程是固定的，可以从以上五个点的任一点开始沿着其中一条线变化，对照五个点的特点依次分析①→⑤和⑤→①对应的两条变化过程表，如表2所示。

表2 两条变化过程表

【总结】利用图像将弹簧产生形变时两个状态对应的各个物理量随形变量变化趋势(非函数关系)反映出来，如图2所示，横轴x表示弹簧的形变量所对应的①②③④⑤五个特殊位置；线b表示v和Ek随形变量x的变化趋势，线c表示a和F合随形变量x的变化趋势，线d表示F和Ep随形变量x的变化趋势。

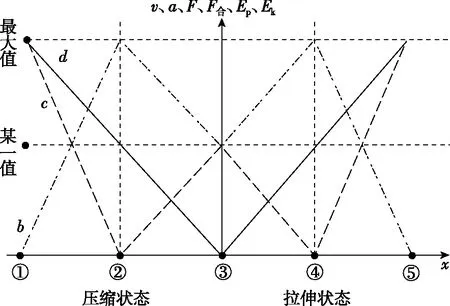
图2 各物理量随弹簧形变量的变化图

2.“一图五点二线”解题程序

含弹簧问题主要考查弹簧处在某一状态时某些物理量的确定或者是某一变化过程中某些物理量的变化，同时还与连接弹簧的物体运动过程密切相关，因此利用“一图五点二线”解决定弹簧问题时，可按以下流程，即定弹簧状态(压缩、拉伸或自然)→定弹簧特殊点(五个点中的其中一个或其他点)→定弹簧变化过程→定与弹簧连接物体的运动过程→定物体所受的外力F外→定物体所受的合力F合→定各物理量的关系式→定各物理量的变化。在这一流程中，可根据问题的实际情况确定分析的起点，中间某些过程也可以不出现，应灵活把握。

3.演绎“一图五点二线”的解题过程

【例1】如图3所示，轻弹簧竖直放置，下端固定在水平地面上，一质量为m的小球，从离弹簧上端高h处由静止释放，某同学在研究小球落到弹簧上后继续向下运动到最低点的过程，他以小球开始下落的位置为原点，沿竖直向下方向建立坐标轴Ox作出小球所受弹力F的大小随小球下落的位置坐标x变化的关系，如图4所示，不计空气阻力，重力加速度为g，以下判断不正确的是

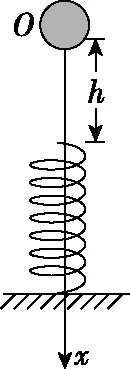
图3

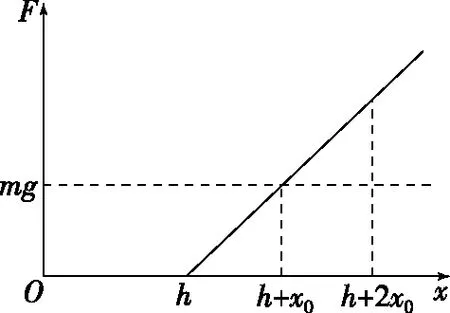
图4

( )

A.当x=h+x0，小球的重力势能与弹簧的弹性势能之和最小

B.小球落到弹簧上向下运动到最低点的过程中，加速度先减小后增大

C.当x=h+2x0，小球的加速度大小为g

D.小球动能的最大值为mgh+mgx0

【答案】D

【解析】A选项：定弹簧状态，当x=h+x0时，弹簧为压缩状态→定弹簧特殊点，x=h+x0对应特殊点②，F=kx0→定与弹簧连接物体的运动过程，小球竖直向下运动且速度达到最大，小球动能Ek达到最大→定物体所受的外力F外=mg→定物体所受的合力F合=0→定各物理量的关系式，由于弹簧和小球组成的系统机械能守恒，则Ek=EpG+Ep弹→定各物理量变化，小球的Ek最大，则小球的重力势能与弹簧的弹性势能之和EpG+Ep弹最小，故A正确。

B选项：定弹簧状态，小球落到弹簧上向下运动到最低点的过程为弹簧压缩状态→定弹簧特殊点，刚落到弹簧上时对应特殊点③，F=0，F合=F外=ma；最低点对应特殊点①，F=2kx0，F合=F外=ma，a达到最大→定弹簧变化过程，对应③→②→①过程→定物体所受外力F外=mg→定各物理量变化，加速度a先减小后增大，故B正确。

C选项：定弹簧状态，当x=h+2x0时弹簧为压缩状态→定弹簧特殊点，x=h+2x0对应特殊点①，F=2kx0，F合=F外=ma→定物体所受外力F外=mg→定物体所受合力F合=mg→定各物理量变化，此时a=g，故C正确。

D选项：定弹簧特殊点，小球动能最大时对应特殊点②→定与弹簧连接物体的运动过程，小球竖直向下运动且速度达到最大→定弹簧变化过程，对应③→②→①过程→定各物理量关系式，对小球由动能定理可得mg(h+x0)-W弹=Ekm-0→定各物理量变化，Ekm>mg(h+x0)，故D错误。

【例2】如图5所示，重10 N的滑块在倾角为30°的斜面上，从a点由静止下滑，到b点接触到一个轻弹簧。滑块压缩弹簧到c点开始弹回，返回b点离开弹簧，最后又回到a点，已知ab=0.8 m，bc=0.4 m，那么在整个过程中

图5

( )

A.滑块动能的最大值是6 J

B.弹簧弹性势能的最大值是6 J

C.从c到b弹簧的弹力对滑块做的功是6 J

D.滑块和弹簧组成的系统整个过程机械能减少

【答案】BC

【解析】滑块从a点由静止下滑到b点接触弹簧后将弹簧压缩到c点，返回b点离开弹簧，最高又回到a点，整个过程没有能量损失，说明滑块运动过程中不受摩擦力作用，滑块和弹簧组成的系统整个过程机械能守恒，故D错误。

对C选项：定与弹簧连接物体的运动过程，沿斜面向下直至速度为0→定弹簧变化过程，对应③→②→①过程→定物体所受外力F外，对物体受力分析得F外=mgsinθ→定各物理量关系式，滑块下滑到c过程由动能定理得0=W弹-mg(ab+bc)sinθ→定各物理量关系式，W弹=6 J，故C正确。

对B选项：定弹簧特殊点，弹簧弹性势能的最大值对应特殊点①→定与弹簧连接物体的运动过程，对应滑块在c点，由功能关系得Epm=W弹=6 J，故B正确。

对A选项：定弹簧特殊点，小球动能最大时对应特殊点②，设该点为b与c间的某一点d，F=kx，Ep为某一值→定与弹簧连接物体的运动过程，滑块沿斜面向下运动速度达到最大，动能Ek达到最大→定弹簧变化过程，，对应③→②过程→定各物理量关系式，对滑块下滑到最大动能过程，由能量守恒可得Ekm=mg(ab+bd)sinθ-Ep→定各物理量关系式，由于mg(ab+bc)sinθ=6 J，所以mg(ab+bd)sinθ<6 J，则Ekm<6 J，故A错误。

4.总结

弹簧最大的特点就是“可拉可压”，并且在“拉”和“压”时产生的弹力方向不同，导致物体的受力也产生变化，使得含弹簧问题比较复杂。涉及弹簧类问题在解题过程中要特别注意弹簧在产生形变过程中的特点，特别是五个特殊位置点，它们既反映弹簧的物理量特点，又反映与弹簧连接物体的运动特点，若将这些特点在分析解题过程中合理运用，就能达到事半功倍的效果。因此，教师在进行相关教学时，可以针对弹簧产生形变的过程先进行系统的分析，并采用图像将形变过程直观的呈现，再将形变过程中的五个特殊位置进行独立的分析，找到各个物理量的特点，进而利用图像将特殊点和形变过程组合起来，最后形成一个知识体系。总之，利用数形结合的思想方法可将复杂问题抽象为具体，简化思路，降低思维难度，从而进一步培养学生分析处理物理问题的能力，提升学生的物理核心素养。