高速平磨氧化锆陶瓷磨削力模型的研究

杜添贺，马廉洁,，邱喆，李红双，毕长波，周云光

(1.东北大学机械工程与自动化学院，辽宁沈阳 110819;2.东北大学秦皇岛分校控制工程学院，河北秦皇岛 066004)

0 前言

氧化锆陶瓷作为一种硬脆材料，它主要的加工方法之一为磨削加工，而磨削力是作为磨削工艺的一个重要参考因素。磨削力不仅直接影响砂轮的磨损、磨削精度，而且对局部接触变形及其性质亦有很大影响。

目前，国内外相关研究者已在磨削力的理论和试验这2个部分开展了相关的研究。李力钧和付杰才[1]根据磨削过程中的磨粒切削刃数和单位面积上的磨屑面积，建立了一个早期的由切屑变形力、摩擦力2个部分组成的关于磨削力预测模型。ZHANG等[2]针对陶瓷基复合材料进行了一系列特殊的表面磨削试验，并基于多重指数函数法建立了磨削力模型，发现磨削参数对磨削力有明显的影响。王君明等[3]基于磨粒与工件之间接触的运动方程理论建立了未变形磨屑厚度的表达式，并在此基础上提出了磨削力的理论模型。CAO等[4]基于砂轮和工件之间相对运动产生的未变形切屑长度，分析了单个活性颗粒的切削作用，建立了碳化硅陶瓷的法向力和切向力模型。AZIZI和MOHAMADYARI[5]提出了一种磨削力模型，包括运动参数，特别是砂轮表面特征，此理论模型可以较为准确地推测磨削力的变化趋势，为相关研究提供一定的根据。LI等[6]建立了磨削YAG单晶时考虑应变率、磨料半径随机分布等因素的磨削力模型，该模型可以很好地分析精密磨削中应变率及固体变形机制对材料去除的作用效果。AGARWAL和RAO[7]依据磨粒形状为半球体，磨粒突出高度服从瑞利分布的概率函数，确定了一个关于工程陶瓷的磨削力和磨削功率的理论模型，并利用试验验证了模型的稳定性。

本文作者根据磨粒突出高度服从瑞利分布的假设，把磨削力分为磨削变形力及摩擦力两部分，引入机床主轴振动修正系数，考虑材料的属性对磨削力的影响因素，最终确定了在高速磨削中氧化锆陶瓷的磨削力理论模型，并利用试验数据对模型的精度进行了验证。

1 未变形切削厚度

1.1 瑞利分布

砂轮表面的磨粒突出高度差别较大，因此关于未变形切削厚度的判断也有多种方法。为了与实际磨粒突出高度的特征更加接近，文中假设砂轮表面磨粒突出高度符合瑞利分布函数的规律，函数表达式如式(1)所示：

(1)

由式(1)可知：只需确定未知量δ，就可得出关于磨粒突出高度的函数关系式。该概率函数分布的数学期望值如式(2)所示:

(2)

1.2 最大未变形切削厚度

平面磨削中最大未变形切削厚度如图1[8]所示，考虑到砂轮上磨粒的实际形状，为了计算未变形切削高度，现作以下两点假设:

(1)磨削中所有突出的磨粒都参与磨削过程，并且切削材料。

(2)砂轮表面磨粒的几何形状接近圆锥状并且尖端处为圆弧，锥角为2θ，其中θ=35°。

图1 最大未变形切削厚度模型

图中：ap为切削深度；ds为砂轮直径长度；li为磨粒在任何位置时的切削深度所对应的弧长；lc为接触的总弧长。

基于以上假设，图2所示为磨粒横截面积示意，单颗磨粒切除工件材料横截面积A的期望值为

(3)

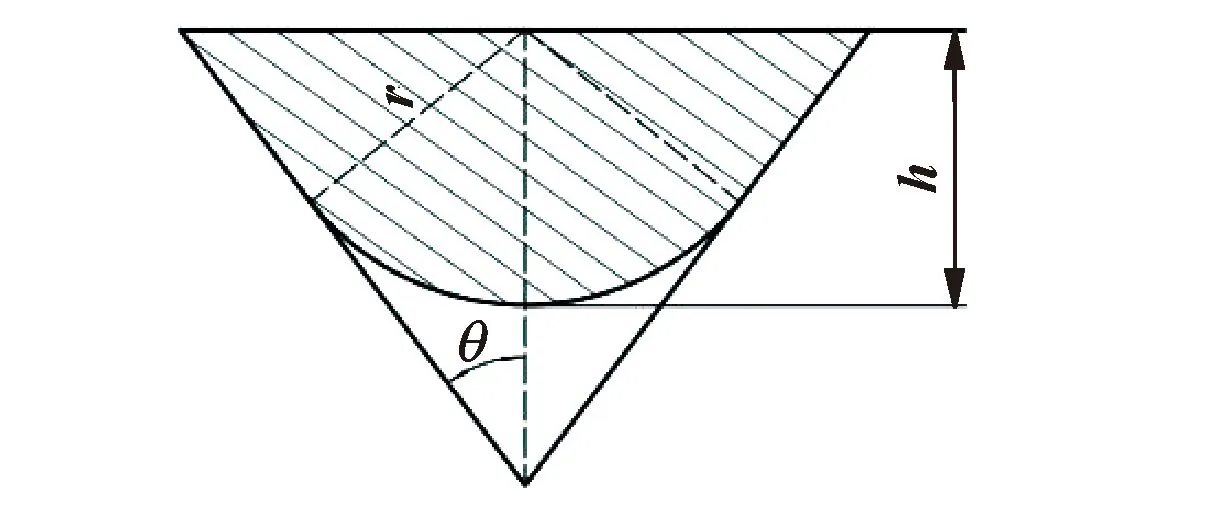
图2 磨粒横截面积示意

则总面积期望值如式(4)所示：

E(Atotal)=NdE(A)=

(4)

按照材料去除率维持不变的特征，材料在微观和宏观时去除的体积前后要保持一致，如式(5)所示：

E(Atotal)vs=bapvw

(5)

式中：vs为砂轮线速度；vw为工件进给速度。

将式(5)代入式(4)可得式(6)：

(6)

由式(2)可得：

(7)

综上，加工接触区内磨粒的平均突出高度即未变形切削厚度如式(8)所示：

(8)

2 磨削力模型

将单颗磨粒磨削力分为磨削变形力和摩擦力两部分[1]，在氧化锆磨削加工过程中磨粒与工件之间接触作用后的受力分析，如图3所示。

在工件与单颗磨粒接触作用的过程中，把摩擦力和切屑变形力分为法向和切向2个方向分别进行分析研究，如式(9)所示：

(9)

式中：Fn为法向磨削力；Ft为切向磨削力；Fnb为法向变形力；Ftb为切向变形力；Fns为法向摩擦力；Fts为切向摩擦力。

图3 单颗磨粒与工件的作用力示意

2.1 单颗磨粒摩擦力

磨粒刚与工件表面接触时，必然发生滑擦过程，此时产生的摩擦力必须要考虑。单颗磨粒与工件之间由于摩擦而引起的摩擦力如式(10)所示：

(10)

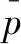
(11)

A0=blcA=b(dsap)1/2A

(12)

则由摩擦而引起的摩擦力整理如式(13)所示：

(13)

2.2 塑性去除单颗磨粒磨削力

图4 磨粒压痕几何示意

当磨粒切削工件时的厚度不超过临界磨削深度时(h≤hp)，氧化锆陶瓷主要表现为塑性去除，临界磨削深度hp对应的弧长为lp。假设磨粒为圆锥状，如图4所示，维氏压头在载荷P的大小作用下以一定速度压入陶瓷材料表面，使其发生塑性变形，在表面形成了一个压痕。负载与材料硬度的关系如式(14)所示：

P=ξa2H

(14)

式中：ξ为压头几何因子，ξ=2。

由图4可知，压痕特征尺寸如式(15)所示：

2a=2htanθ

(15)

实际精密磨削中，机床主轴的振动会对工件表面及亚表面质量造成严重损伤，因此需要考虑主轴振动对磨削力的影响，文中引入了主轴振动修正系数λ。塑性去除下的法向变形力Fnb关系式如式(16)所示：

Fnb=λξh2Htan2θ

(16)

式中：λ为介于0～1之间的常数，文中根据试验取λ=0.15。

由几何分析可得单颗磨粒的法向、切向磨削力之比[10]，获得切向变形力如式(17)所示：

(17)

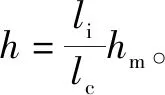
则材料在塑性去除状态下的磨削力如式(18)所示：

(18)

2.3 脆性去除单颗磨粒磨削力

在加工过程中，当磨粒切削深度超过临界磨削深度时(h>hp)，材料主要表现为脆性去除，此时去除方式主要为材料的剥落，其中裂纹的产生和扩展是材料发生断裂碎裂的主要因素。

如图5所示，依据压痕断裂力学，随着法向载荷的增加，纵向裂纹首先在弹性变形区下面形成和扩展；卸载过程中，由于弹塑性区的残余应力不匹配，将产生横向裂纹，材料被去除[11]。

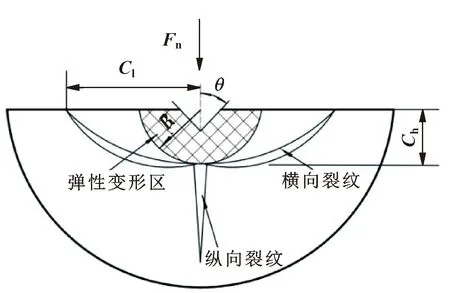
图5 压痕断裂力学模型

横向裂纹的深度和长度如式(19)和式(20)所示：

(19)

(20)

式中：C2为常数，C2=0.226 ;ν为材料泊松比，ν=0.3。

图5所示的变形区近似半径为B的半圆，函数关系式为载荷和材料特性的函数[12]，如式(21)所示：

(21)

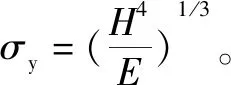
如上所述，横向裂纹始于塑性变形区的底部，半径B近似等于Ch，同时考虑主轴振动影响，可以推导出脆性断裂状态下的磨削力如式(22)所示：

(22)

将式(22)化简，令

则式(22)可整理为式(23)的形式：

(23)

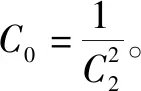
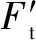
(24)

将式(18)和式(23)代入可得磨削力模型为

(25)

3 试验条件

试验在XD-40A数控机床上进行，采用瑞士Kistler公司的六分量测力仪对磨削力进行测量，试验装置如图6所示。采用树脂结合剂金刚石砂轮进行磨削，其型号为MBD61A1/T2200#100% B125*12*32*5,工件为直径25 mm、厚度3 mm的氧化锆陶瓷片。表1所示为材料参数。

图6 磨削试验装置

表1 氧化锆陶瓷材料性能参数

4 磨削力模型的试验验证

为验证文中提出的磨削力理论模型，分别以砂轮转速、进给速度和磨削深度为单因素变量，每个试验重复3次，取平均值作为试验结果。进行了15组单因素试验，根据理论模型计算相关参数条件下的磨削力,并与试验数据进行了对比。

图7—图9所示为磨削力试验值、理论值与各个参数之间的影响作用关系。可见在文中试验的参数范围内，氧化锆陶瓷磨削试验中磨削力随砂轮转速的提高而减小，随工件进给速度、磨削深度的升高而增加。其中，以砂轮转速为变量下，单位宽度上的法向磨削力的理论值与试验值的平均相对误差为8.04%，切向磨削力误差为8.84%；以进给速度为变量下，单位宽度上的法向磨削力的理论值与试验值的平均相对误差为7.22%，切向磨削力误差为7.86%；以磨削深度为变量下，单位宽度上的法向磨削力的理论值与试验值的平均相对误差为9.32%,切向磨削力误差为7.2%。

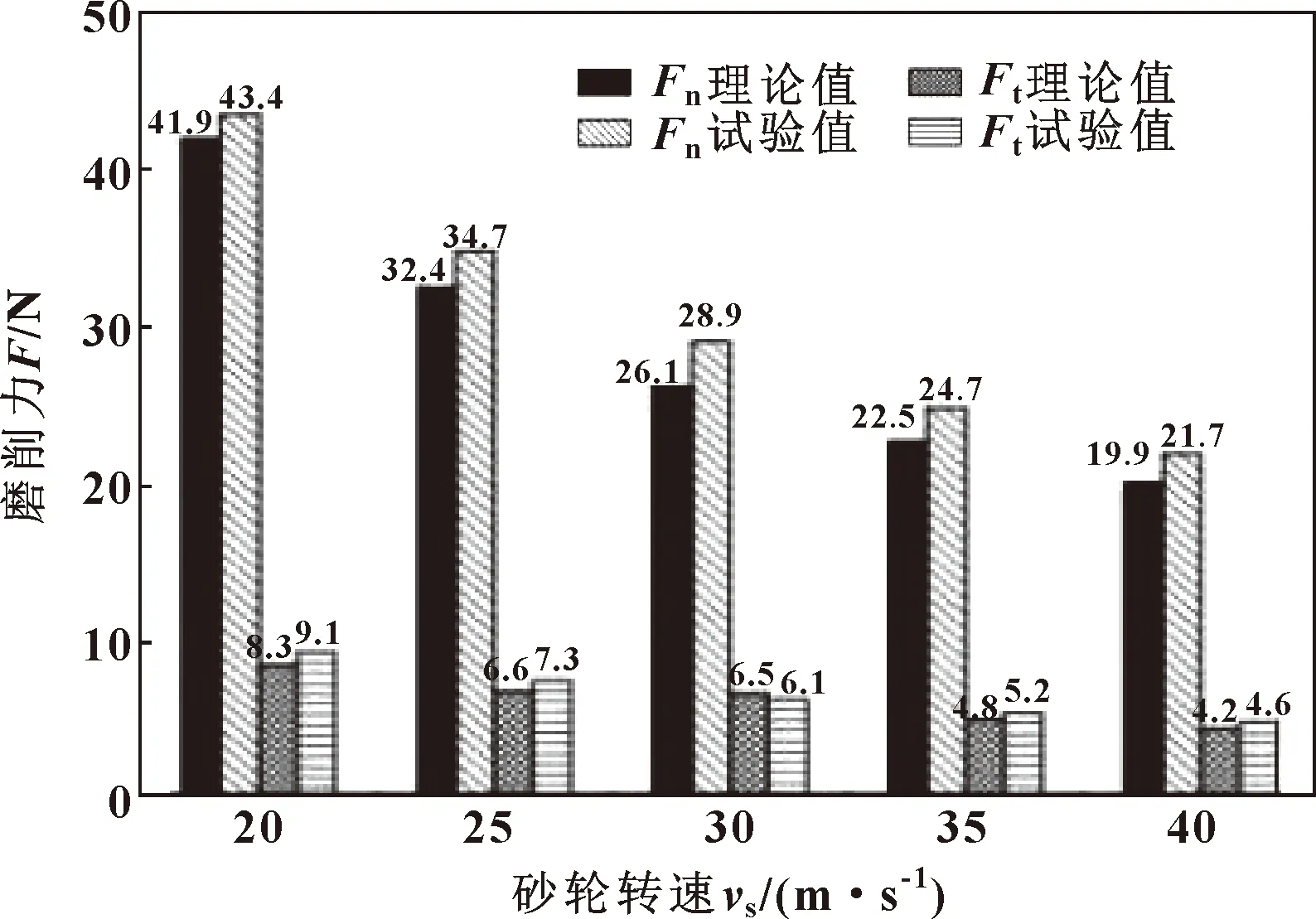
图7 单位宽度磨削力与砂轮转速的关系(工件进给速度3 000 mm/min，磨削深度10 μm)

图8 单位宽度磨削力与进给速度的关系

图10所示为各试验组别下切向、法向磨削力试验值和理论值之间的误差分析比较。可以观察得到：该模型法向、切向综合磨削力平均误差分别为8.19%和7.97%，误差最大值不超过15%，误差在允许范围之内,证明该理论模型合理有效。

氧化锆陶瓷磨削试验中误差产生的原因可能是随着磨削加工过程的进行，砂轮逐渐磨损导致磨粒的半径发生了变化。同时磨削过程中材料的微观结构也会随着砂轮与工件的摩擦、挤压而发生演变，在脆性去除过程中材料的表面和亚表面会产生裂纹，导致材料的硬度等参数降低，磨削力的实际测量值会小于预测值。并且在建立理论模型的过程中也对相关步骤进行了理想化的假设和简化，使得磨削力的理论模型计算值和试验值之间存在了一定的误差。

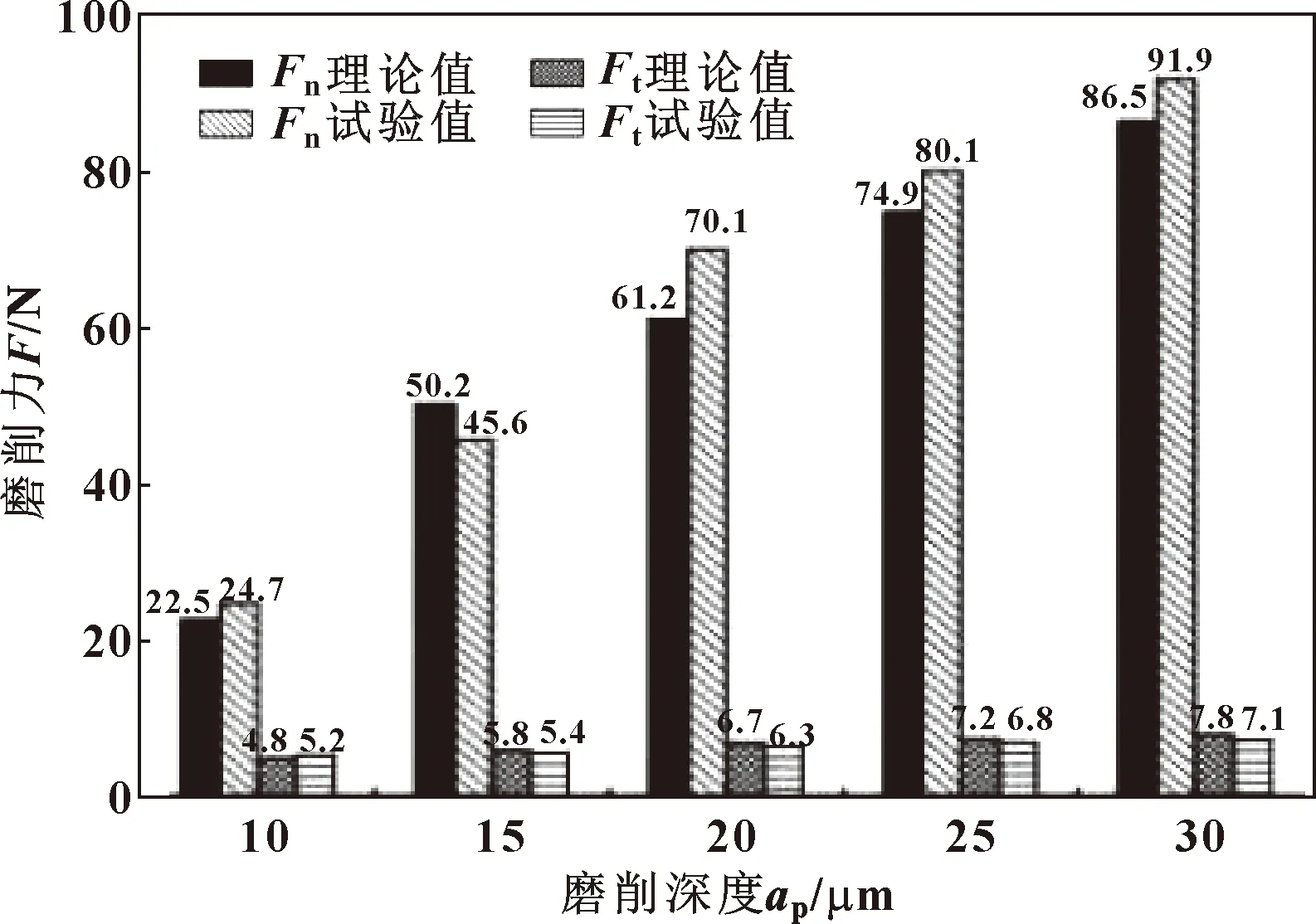
图9 单位宽度磨削力与磨削深度的关系

图10 切向、法向磨削力试验值和理论值误差比较

5 结论

(1)建立磨粒突出高度服从瑞利分布的未变形切削厚度理论模型，将磨削力分为磨削变形力和摩擦力2个部分组成,考虑加工过程中机床主轴的振动影响，引入主轴振动修正系数，建立了氧化锆陶瓷磨削力理论模型。

(2)通过单因素试验验证，发现磨削力随砂轮线速度的增大而减小，随进给速度和磨削深度的升高而增大，模型理论值和试验值的变化趋势保持一致。磨削力在法向、切向上的平均误差分别为 8.19%和7.97%，误差最大值不超过15%。