基于DTW相似度和Bi-LSTM的滚动轴承寿命预测
周建清,朱文昌,王恒
(1.常州市高级职业技术学校电气工程学院,江苏常州 213161;2.南通大学机械工程学院,江苏南通 226019)
0 前言
滚动轴承作为机械设备的核心部件,其性能好坏直接影响设备能否正常运行,因此,在轴承损坏前预测其剩余使用寿命,避免设备损坏造成的财产损失及人员伤亡,具有重大研究价值[1-2]。
近年来,以数据驱动为主的深度学习算法在滚动轴承寿命预测方面得到了广泛的应用,主要围绕2个问题展开:(1)选择合适的深度学习算法或对深度学习算法进行优化,提高预测的准确率;(2) 构造出单调性好、对轴承异常敏感的退化指标训练神经网络,使其充分挖掘并学习轴承的退化信息以提高预测精度。在滚动轴承寿命预测算法选择方面,目前以长短期记忆神经网络(Long Short-Term Memory,LSTM)为代表的深度学习算法得到了广泛应用。刘小勇[3]根据滚动轴承原始数据构建退化指标,将退化指标作为LSTM网络的输入,完成对滚动轴承寿命的预测,并验证了深度学习算法与传统的机器学习算法相比具有更高的预测精度。NGUYEN和MEDJAHER[4]利用LSTM进行寿命预测,给出了系统在不同时间窗下的故障概率,以平均成本率为标准,获得了比周期性预测策略和理想预测维护策略更好的结果。WANG等[5]对LSTM预测算法进行了改进,将双向长短时记忆网络 (Bi-directional Long Short-Term Memory,Bi-LSTM) 应用于负荷的短期预测并取得了很好的试验效果。在构建轴承退化指标的研究中,孟文俊等[6]提取滚动轴承时域、频域特征并通过主成分分析进行融合,但构造出的融合指标单调性较差,数据波动较大;韩林洁[7]利用单卷积神经网络(Convolutional Neural Network,CNN)提取出滚动轴承的退化信息,输入进门控循环单元(Gated Recurrent Unit,GRU)实现了轴承的寿命预测,但单卷积神经网络提取出的特征较为单一,容易造成信息损失;胡城豪等[8]提出一种多尺度卷积神经网络,克服了单卷积神经网络的问题,但卷积神经网络中的卷积核个数及卷积核大小的设定依靠经验而定,缺乏一定的科学性。信息熵指标作为一种传统退化指标,可用于量化信息的不确定度,具有较好的鲁棒性及稳定性,被广泛应用于轴承故障诊断[9]、退化评估[10]及寿命预测[11]中,然而信息熵对轴承异常不敏感,难以准确刻画轴承的退化历程[12]。动态时间规整算法(Dynamic Time Warping,DTW)可用于计算时间序列的相似度,通过对时间序列进行伸缩、对齐及规整等操作可准确描述时间序列间的相似度与差异性。NGUYEN[13]利用DTW算法计算时间序列间的相似性并进行状态匹配,与欧几里得距离相比,它对时间序列相似度的计算更为准确。LI等[14]利用DTW算法分析手语运动轨迹间的相似性,判断它们是否属于同一类别,提高了手语轨迹识别的准确率。将DTW用于计算信息熵指标间的相似度,实现对信息熵指标优化的目的,进一步提高该指标对轴承异常的敏感程度。
综上,本文作者用动态时间规划算法优化信息熵指标,将相似度作为滚动轴承健康指标,结合Bi-LSTM实现滚动轴承寿命的预测,结果表明了该方法的有效性和可行性。
1 滚动轴承健康指标的构建
1.1 基于信息熵的轴承特征提取
根据轴承健康监测信号采集特点,在监测时间T内传感器共采集轴承信号M次,每次采集到N个数据点,每个点记为x(m,n),故tm时刻采集到的数据刻构成列向量x(tm):
x(tm)=[x(m,1),x(m,2),…,x(m,n),…,x(m,N)]T1≤m≤M,1≤n≤N
(1)
通过M次采集到的轴承数据X=[x(t1);x(t2);…;x(tm);…;x(tM)]为二维数据集合,其第一维是时间维度,记录轴承从正常到失效的整个过程;第二维为空间维度,记录同一时刻下轴承不同位置的状态信息。由于不同时刻采集到的轴承数据具有不同的分布特性,基于此特性本文作者采用信息熵提取不同时刻轴承信号的分布特征。
1984年SHANNON提出了信息熵的概念用来解决对信息的量化度量问题[15]。在信息论中,一个系统越稳定,其信息熵越小,tm时刻轴承信息熵的计算如式(2)所示:
(2)
式中:P[x(m,n)]表示x(m,n)出现的概率。
在监测时间T内计算出不同时刻的信息熵,得到退化特征序列F:
F=[S(t1),S(t2),…,S(tm),…,S(tM)]
(3)
虽然信息熵可表征数据整体的分布特性,但由于相邻时间段间熵值信号变化较为微弱,难以准确表征滚动轴承退化的各个阶段,需对它进行优化处理。
1.2 基于DTW的滚动轴承健康指标构建
滚动轴承的退化具有连续性及不确定性,轴承当前退化状态虽与前n个状态有关,但当前轴承的前后两个退化状态具有较大差异性,并随着退化的加剧,正常状态、早期异常及严重故障状态下的数据间的差距将逐渐增大,通过分析不同时间段下数据的差异性可更好地描述轴承的退化状态,动态时间规整算法能准确计算出时间序列间的相似性(差异性)。利用DTW算法优化信息熵指标,计算不同阶段熵值指标的相似度,将它作为健康指标,用于表征轴承的退化历程。
在计算相似度之前,选定轴承正常状态下的时间序列作为参考模板P,同时利用时间窗遍历轴承退化序列F构造测试模板Q,设置时间窗规模为1×g,对退化序列F进行信息锁定。在采样时刻tm下构造出的测试模板为
Q(tm)=[S(tm-g),S(tm-g+1),…,S(tm-1),S(tm)]
(4)
设定参考模板P不变,测试模板Q随时间tm而改变,计算两者间的相似度,并用于反映当前轴承退化状态与正常状态间的差异性。由于DTW算法在时间序列间相似性计算方面更优,故将相似度作为健康指标可更好地表征轴承的退化历程。
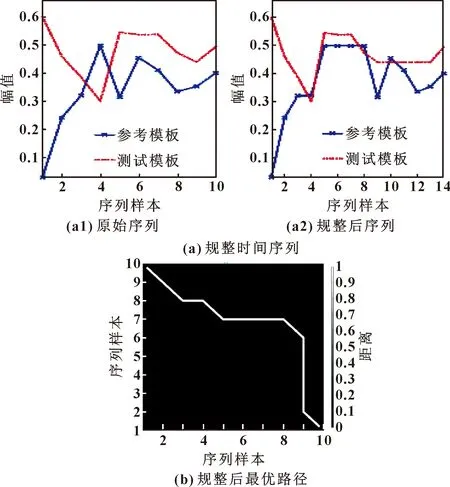
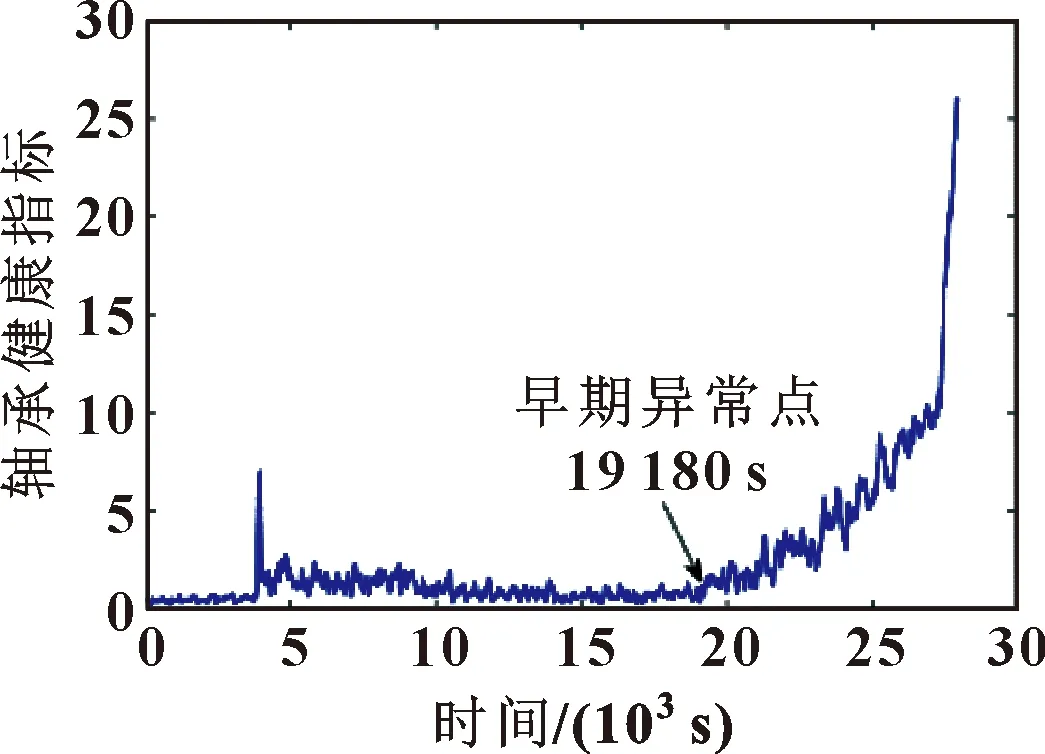
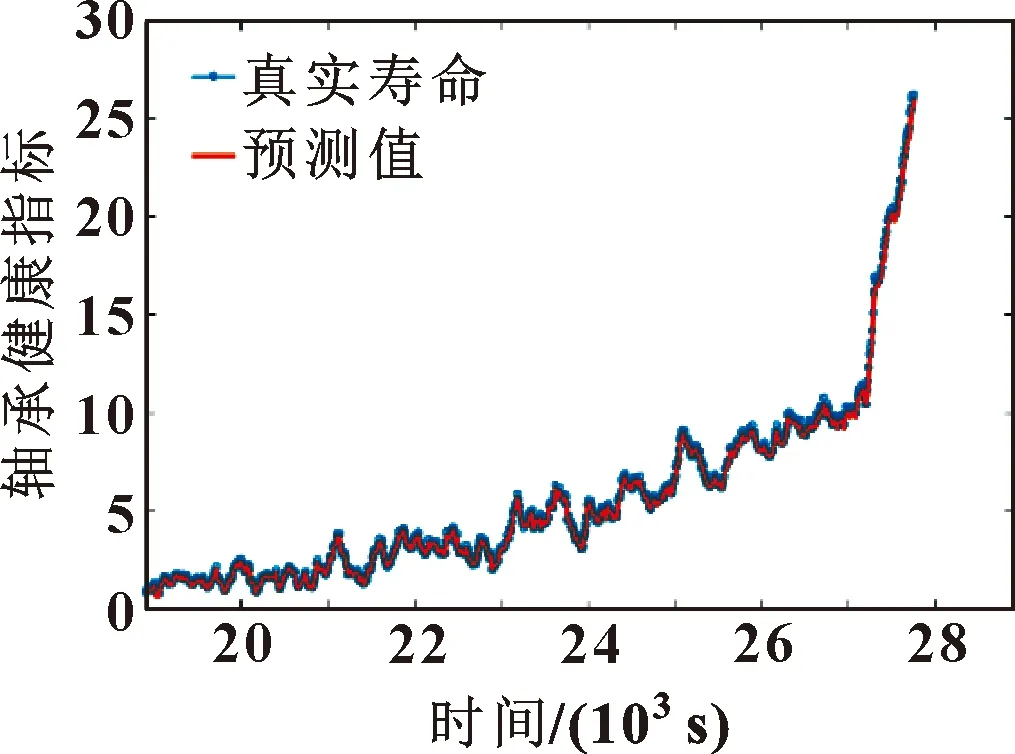
假设构造出的参考模板为P=[p1,p2,…,pl,…,pL](1 (5) 当w遵循边界性、单调性及连续性的约束时[16],P和Q之间所有对齐路径的集合记为AP,Q。DTW算法的目标是最小化两条时序数据中所有对应数据点的局部距离之和,其定义如式(6)所示: (6) DTW算法采用动态规划思想,利用递归公式(6)将以上问题转换为对P和Q子序列问题的求解: (7) 通过计算路径的距离可有效实现轴承的不同序列模板间数据的相似性,相似性越大则距离越小,利用它对信息熵退化指标进行优化并构建健康因子。 双向长短期记忆网络是对长短期记忆神经网络的一种延伸,它由一个前向LSTM与一个后向LSTM组成,能够对输入数据进行正向和反向遍历[17]。LSTM模型如图1所示。 由图1可知,每个LSTM单元都配有3个控制信息流的门,每个门均包含一个激活函数和一个逐点乘法运算。遗忘门控制信息流;输入门决定哪些信息比较重要以便记忆;输出门决定将要传递的信息。3个门的值设置在0和1之间。其工作步骤如下: (1)遗忘门决定应该记住或遗忘哪些信息,如式(8)所示: ft=σ(Wf[at-1,xt]+bf) (8) 式中:at-1表示上一时刻的隐层信息;xt表示当前输入;Wf与bf分别表示LSTM网络的权值和偏置,均为模型训练参数;σ表示激活函数sigmoid。 图1 LSTM模块示意 (2)输入门确定需要保存的信息,如式(9)所示: Ct=ft*Ct-1+σ(Wi[at-1,xt]+ bi)*tanh(Wc[at-1,xt]+bc) (9) 式中:Ct-1为前一个细胞的状态;Ct为当前细胞状态信息。 (3) 输出门决定要传递的信息,如式(10)所示: at=σ(Wo[at-1,xt]+bo)*tanh(Ct) (10) Bi-LSTM神经网络在LSTM网络的基础上进行了改进,每个训练模块的输出层都包含一个前向LSTM和一个反向LSTM网络,如图2所示。其输出包括上下文的特征信息,理论上较LSTM可提高预测的准确度[18],文中采用Bi-LSTM对滚动轴承剩余寿命进行预测。 图2 Bi-LSTM模块示意 综上所述,本文作者基于信息熵及DTW算法构造出滚动轴承健康指标用于表征轴承的退化状态,结合Bi-LSTM网络可实现轴承寿命的预测,其算法流程如图3所示,具体步骤为: (1)利用信息熵提取滚动轴承的时域退化特征; (2)提取退化指标F的正常时间序列作为参考模板P,利用时间窗遍历指标F不同时刻的退化信息并构造测试模板Q,利用DTW算法计算相似度,并将它作为健康指标用于表征轴承的退化; (3)将优化后的指标分为测试集及训练集,训练Bi-LSTM网络并预测轴承寿命。 图3 文中所提算法流程 试验数据来自法国IEEE PHM 2012 Prognostic challenge提供的公开数据集,试验装置如图4所示,采集到的试验数据分为训练数据及测试数据,取Bearing1_1轴承训练数据集的水平振动加速度信号进行分析,试验轴承转速为1 800 r/min,所受载荷为4 000 N,传感器采样频率为 25.6 kHz,采样间隔为10 s,当振动加速度信号幅值达到20g时轴承失效,此过程共采集到2 803组数据。 图4 轴承加速度寿命试验装置 对Bearing1_1轴承数据按上文所述方法进行处理,取熵值指标正常状态下的时间序列为参考模板,测试模板与参考模板中特征矢量长度均为10。利用Bi-LSTM算法预测轴承寿命时,设定Bi-LSTM网络含有两个LSTM层,隐含层神经元个数为50,激活函数为Relu,ADAM用于梯度优化,输入层节点数为10,输出层为1,学习率为0.01。 按照第1节所述方法对Bearing1_1数据集进行处理,构造出的熵值指标与传统峭度指标相比,熵值曲线单调性较好,所受的扰动更小,鲁棒性较强,但其变化较微弱,无法明显辨识轴承早期异常的发生,难以准确区分轴承退化的不同阶段,如图5所示。 图5 轴承Bearing1_1的熵值指标及峭度指标 为提高指标的表征性能,采用DTW算法对其进行优化,提取110~200 s的信息熵指标作为参考模板,分别提取210~300 s与26 010~26 100 s的熵值指标作为测试模型进行相似度的计算。当提取210~300 s的熵值作为测试模板计算其余参考模板间的相似度时,DTW算法先对两个序列的各个点进行缩放及对齐处理,如图6(a)所示。在进行路径规整后,最优路径从数量较小的深色区经过,路径的累计距离即为两个序列间的相似度(图6(b)),此时累计距离较小为0.563。这是由于两个序列都处于正常状态,虽然原始序列间存在一些细微的差距,但是所蕴含的轴承退化信息较为相似,通过DTW算法缩放、对齐及规整后两序列基本一致,累计距离较小。在参考模板不变的情况下,选定26 010~26 100 s的特征序列作为测试模板计算相似度时,由于参考模板与测试模板间差异较大,DTW算法无法将两模板对齐,最终规整后的路先经过浅色区域,累计距离较大为24.785,如图7所示。利用此算法对信息熵退化指标不同阶段数据进行遍历,计算其相似度,可构建出如图8所示的健康指标。健康指标在19 180 s之前整体较为稳定,在此时刻之后,曲线整体有较为明显的上升趋势,故将此时刻定义为Bearing1_1的早期异常点。与图5中的峭度指标与信息熵指标相比,经过相似度优化后的健康指标能更明显检测出轴承异常的发生,证明该方法有效性。 图6 210~300 s轴承相似度计算 图7 26 010~26 100 s轴承相似度计算 图8 基于DTW优化后的健康指标 第2.2节中构建出了滚动轴承的健康指标并检测到轴承在19 180 s后进入退化状态,提取0~19 180 s的健康指标对Bi-LSTM算法进行训练,并用训练好的网络对19 180 s后的轴承数据进行滚动轴承寿命的预测,结果如图9所示。 图9 基于健康指标及Bi-LSTM的轴承寿命预测 为验证所提出的方法(Entropy-DTW-Bi-LSTM)的准确性,将它与Entropy-DTW-LSTM算法、Entropy-Bi-LSTM算法及Entropy-LSTM算法进行对比试验,取均方误差(Mean Squared Error,MSE)与相关指数R2对其进行评价,如公式(11)所示: (11) 式中:fpred,i为第i个序列对应的预测值;fact,i为第i个序列对应的真实值;fmean为真实值的均值。 在LSTM网络隐藏层神经元个数、学习率、激活函数等网络参数不变的情况下,对比上文中提到的几种算法的预测结果,如表1所示。可知:文中所提出的滚动轴承寿命预测算法预测结果的eMSE更小、相关指数R2值更大,更为接近真实寿命曲线。同时,当基于数据驱动的滚动轴承寿命预测算法难以明显提高寿命预测精度时,通过改变轴承健康指标的性能,提高其单调性及对异常点敏感性可有效提高算法预测的精度。 表1 各模型预测结果对比 本文作者通过DTW算法研究滚动轴承不同阶段下熵值指标时间序列间的相似性,构造轴承健康指标结合Bi-LSTM算法,实现了轴承异常的检测及寿命的评估,得出以下结论: (1)与传统指标相比,基于DTW算法优化信息熵值指标后构造出的健康指标的单调性及鲁棒性较强,且对轴承的早期异常更敏感,为轴承状态退化评估提供了一种新的研究方法; (2)将DTW优化构建出的健康指标结合Bi-LSTM的寿命预测算法与其他预测方法相比,当基于数据驱动的算法难以明显提高轴承预测精度时,通过优化健康指标可进一步提高预测效果。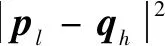
1.3 基于Bi-LSTM的轴承寿命预测



2 应用研究
2.1 数据来源

2.2 滚动轴承健康因子构建


2.3 基于Bi-LSTM的轴承寿命预测

3 结论

