典型工况下桥式起重机大车运行机构摆角模型
余震,王海兰,余进,胡柯,任豪豪
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北武汉 430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北武汉 430081)
0 前言
作为装备制造业领域的重要设备之一,桥式起重机在各行各业具有广泛应用。随着作业环境以及作业要求的改变,对起重机精准定位以及防摇要求愈来愈高,抑制起重机的摇摆能有效提高其工作效率,能更好地促进工业自动化的进程和保证工业系统的安全运行。
桥式起重机在工作过程中摇摆的一个重要原因是其大、小车运行机构和主、副起升机构在工作过程中的加减速运动而产生了冲击,这个原因决定了起重机防摇摆研究的3个方向:人工防摇、机械式防摇、电气式防摇(如表1所示[1])。随着控制技术的不断发展,现在主流的防摇控制策略是电气式防摇[2]。
针对桥式起重机防摇摆控制的数学模型构建方面的研究,国内外有许多学者取得了相应的成果。文献[3-4]研究了吊运过程中吊重的摆动现象,将系统简化成双摆振动模型,采用分析力学的方法建立系统的拉格朗日方程,得到系统微分方程。文献[5]考虑负载与吊具的体积,建立了考虑分布式质量梁的双摆起重机动力学模型,设计了4种版本的分层滑模控制方法,又通过仿真与实验验证了此方法在解决桥式起重机双摆问题时的可行性与有效性[6]。
对于起重机防摇摆数学模型的研究,以上学者都是把整个桥架结构视为刚性体,假定初始负载摆角为零度,实际上由于吊绳为挠性体以及操作等因素,起重机初始摆角会不可避免的存在。文献[7]推导出在牵连惯性力、相对惯性力、科氏力和离心惯性力的作用下变截面梁受移动质量作用的横向弯曲振动方程,并采用Newmark法进行数值求解。文献[8]将小车架设为弹性结构,考虑起重机主梁的横向变形,建立了门式起重机三质量三自由度系统振动模型,得到更准确的门式起重机防摇系统数学模型。文献[9]分析了起重机垂直变形对摇摆控制的影响,提出了大车静止时的小车三维三自由度弹性动态模型,并用MATLAB验证了模型的有效性。
本文作者根据起重机实际作业循环进行载荷分析,基于牛顿第二定律建立大车在负载作用下的运动过程动力学微分方程,并充分考虑风扰、轨道缺陷、驱动力、钢丝绳弹性形变等因素对摆角的影响,再将现有的标准起重机参数导入吊重模型进行了MATLAB仿真分析,根据仿真结构进行模型优化,在一定程度上确保起重机在实际工况下的动力学模型的准确性。

表1 部分防摇策略
1 桥式起重机典型工况与载荷分析
1.1 桥式起重机结构
桥式起重机由桥架结构、运行机构、起升机构、电气装置四部分组成(如图1所示):
(1)桥架结构承受起重小车的重力,由端梁、主梁、栏杆、走台、轨道和司机室等构成。
(2)运行机构细分为大车运行机构和小车运行机构,驱动起重机大、小车的车轮分别沿着其各自轨道运行,完成规定的运动。

图1 桥式起重机实物
(3)起升机构实现物料的升降运动,主要由电机、滑轮组、钢丝绳、制动装置和其他相应的安全装置组成。
(4)桥式起重机的电气系统包括电气设备和电器线路。供电装置、保护箱、照明设备、电器线路、电气主回路、照明信号回路及控制回路等组成起重机电气线路。
1.2 桥式起重机工作流程
一般情况下,在一次完整起吊过程中主要的工作流程为:(1)负载起升过程是将吊重提升至指定高度以进行下一步的运输;(2)通过大车和小车的驱动将吊重搬运至目标位置前方或者上方;(3)将吊重自目标位置上方垂直落下,结束此次工作行程。在实际操作过程中,以上3个步骤依次进行。
引起起重机工作过程中摇摆的原因主要有两方面:一是起重机的大、小车运行机构和主、副起升机构在工作过程中的加减速运动而引起的吊重摆动;二是在作业过程中的一些不确定因素引起的摆动,包括起重机在作业过程中受到的风载荷、操作人员的操作失误、轨道高低差等。文中从引起摆动的不同因素出发,分析起重机摆动因素,并构建其摆角数学模型。
1.2.1 起重机取物起升阶段载荷分析
一般来说,起重机取物起升过程分为3个阶段:第一阶段,起升机构启动瞬间,钢丝绳是松弛状态,钢丝绳由松弛到拉直,忽略钢丝绳自重,钢丝绳不受力,等效起升重物静止不动;第二阶段,钢丝绳状态由拉直到拉紧,钢丝绳受力从0增加到Q,起升钢丝绳从不受力状态到拉力逐渐增大,通过卷筒及其支撑构件将力F2(t)作用在桥架上,间接造成桥架受到的作用力由零开始逐渐增大,但仍然没有离地。图2所示为负载离地后第三阶段,吊重开始离开地面并与结构发生共振,此时钢丝绳受力达到最大,且起升机构产生的动载荷最大。由于滑轮组中各个滑轮所受阻力大小不一,因此使得吊重产生的拉力不能均衡分配到每段绳索上,导致绳索张力不统一,使系统成为弱阻尼系统,从而造成负载轻微摆动。由于初始摆动的存在,大小车的加速运动会使摆动更加剧烈,因此模型的最终结果应该包括这部分产生的振动摆角[10]:
Fjmax-Δl×k×cosθ=Q
(1)
式中:Fjmax为作用在大车的钢丝绳最大拉力;Δl为钢丝绳升长量;k为钢丝绳材料的弹性系数;θ为钢丝绳摆动后与竖直方向的夹角;Q为起吊重物重力。
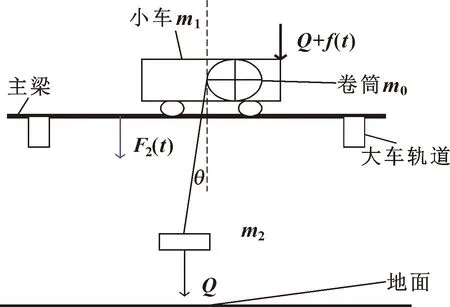
图2 负载离地后
1.2.2 起重机大车加速阶段载荷分析
起升机构起升负载后,需将负载吊至目标位置前方或者上方,此时起重机及其车轮等结构受到水平载荷作用。在起重机实际作业过程中,很少出现大车、小车联动的情况,通常情况下大小车单独运动,即使在联动情况下,在联动方向上的运动规律与小车单独运动规律相同,因此在载荷分析中单独考虑大车的运动情况。除了驱动电机提供的驱动力外,起重机在沿轨道水平方向还有以下载荷:
(1)移动质量水平惯性力Fh
大车移动的水平惯性力是起重机自身重力和负载在大车运行机构启动或者制动时产生的沿轨道方向的水平惯性力,包括整机惯性力Fh2、带载小车惯性力Fh1:
Fh=Fh2+Fh1
(2)
(2)轨道给车轮的滚动摩擦Fr以及起重机转动机构的结构阻力Fc,构成了两侧车轮的总行走阻力:
(3)
式中:c为转动机构轴承摩擦因数;d为大车车轮轮轴枢直径;D为大车车轮踏面直径;f为滚动摩擦因数;∑Fmi为车轮轮压[11]。
(3)起重机偏斜移动时水平侧向力Fs
由于轨道、车轮等在制造与安装时存在一定的误差,以及大小车轨道上表面不平、两侧驱动电机的转速或走轮直径有差异等因素的影响,沿着轨道运行的起重机,在运行过程中将在车轮轮缘与轨道侧面摩擦产生水平侧向推力,此时还会产生附加阻力Fz,从而导致负载产生断断续续的摆动。
(4)y方向风载Fdy
起重机在室外作业时会受到风载,风载与风压和起重机的迎风面积有关,因此在构建起重机运动过程中的摇摆模型时,必须考虑因风载作用而产生的负载偏摆影响。
Fdy=S×C×p×Kh
(4)
式中:p为计算风压;S为迎风面积;Kh为风压高度变化系数;C为风力系数。
2 起重机系统的动力学分析与建模
2.1 起重机在一个工作循环内的运动学分析
图3所示为起重机大车运行时在水平载荷作用下的负载摆动(坐标系为笛卡尔三维坐标系),可以看出:当起重机工作时,重物会通过绳索以小车的悬挂点进行摆动,摆动角度为θ。对摆动角度θ沿起重机前进方向与重物在桥梁上面横向的移动方向上进行分解,分别投影在yoz和xoz平面,得到θx与θy。Fx和Fy分别为驱动大、小车运动的驱动力;fx、fy分别为大、小车受到的摩擦阻力;a1、a2分别为大、小车沿运行方向的加速度;y(t)和x(t)表示对应的y与x方向上的移动位移;mt为负载质量,m1和m2分别为大车桥架结构(包括走台、主梁、端梁、小车等结构)和小车等效质量。因轨道存在高低差,轨道2个上表面不在同一平面,大车车身与水平面呈一夹角α;Fdy、Fdx为施加在负载上的风载。
根据已有研究[12]得知,当进行起重机完整作业循环时(即先进行吊重的起升,随后大车沿轨道运行,接着小车沿大车轨道运行,最后进行吊重下降的过程),此时吊重的运动轨迹类似在球面做圆周摆动运动,从宏观上分析,负载摆角θ可以分解为大、小车在一个二维平面内运动而产生的摆角。在构建起重机运动过程中摇摆摆角数学模型时,为简化模型构建,作出如下假设:
(1)大、小车运动过程相互独立;
(2)忽略桥式起重机系统机械结构的弹性形变;
(3)假设小车车轮与小车轨道的摩擦为理想的滚动摩擦,摩擦因数恒定;
(4)将钢绳视为无质量吊绳,且忽略它与小车起升机构滑轮及卷筒处的摩擦;
(5)假定钢丝绳理想地缠绕在卷筒槽和滑轮上,并且起升或下降过程中不打滑和滑转;
(6)由双轨不在同一平面而产生的附加阻力统一纳入车轮滚动摩擦中;
(7)假设Fy完全受变频器输出的影响,忽略减速器和小车电机等一些非线性因素。

图3 在一个工作循环内的起重机运动模型
2.2 起重机工作过程中的大车运行方向摆角数学模型构建
(1)吊重起升阶段产生的初始摆角
许多学者研究起重机起升机构时将钢丝绳视为刚体,尽管建模时简化了钢丝绳的计算,但这不够严谨。实际上,钢丝绳是一个弹性体,缆绳在负载作用下会产生弹性变形,图4所示为起重机起吊重物离开地面并且开始加速运动过程中,重物偏离竖直方向的示意。可知:当吊重与钢丝绳保持静止时,此时钢丝绳受到的合拉力为负载重力Q,设Δl1和Δl2分别为左右两根钢丝绳在拉力载荷作用下产生的弹性伸长量(单位为mm),由虎克定律可知:每根钢丝绳承担的载荷值分别为Δl1×k、Δl2×k(k为钢丝绳的刚度系数[13])。设穿过该滑轮组有n组钢丝绳,对吊重进行受力分析,则:
(5)
(6)
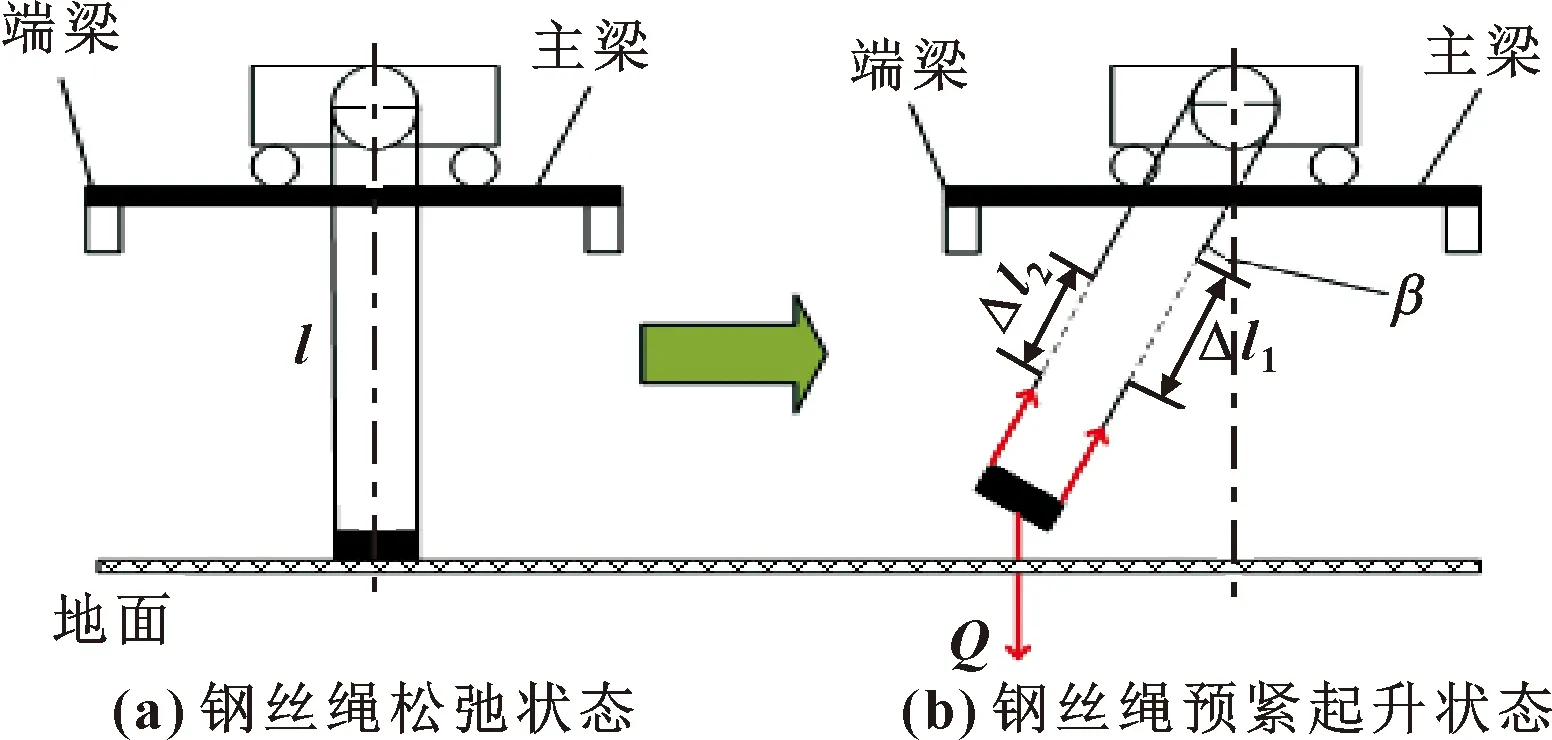
图4 吊重起升阶段摆角示意
绳长伸长量与起重力有以下关系[14]:
(7)
式中:Fjmax为绕入卷筒的钢丝绳最大静拉力(为便于计算,假设每根钢丝承受的拉力相同,且都为最大张力);Q为起升载荷及吊具重力之和;ih为滑轮组倍率;ηh为滑轮组效率;E为钢丝绳等效弹性模量;l为钢丝绳的总长度;L为不受力时卷筒以下钢丝绳的全长;A为钢丝绳截面积;F为在指定滑轮组倍率下单绳最大拉力。由此可得起升钢丝绳初始摆角为
(8)
(2)大车运行双轨不在同一水平面
桥式起重机在安装以及长时间作业过程中,不可避免地会发生沉降、变形、倾斜等情况。依据《桥式和门式起重机制造及轨道安装公差》的要求,如轨道间高低差超过±10 mm时,就会因荷载出现横向滑移,运行机构水平受到的力就会发生改变,从而加剧负载摆动。轨道高度差示意如图5所示。

图5 轨道高度差示意
参照图3所示构建其载荷分析图,由于大车双轨不在同一平面而会产生一倾斜夹角(如图6所示),并将产生的附加阻力Fz统一纳入车轮滚动摩擦中,根据《起重机设计规范》(GB/T 3811—2008)中规定,起重机偏斜侧向力的求解经验公式为
(9)
Fz=ζ×Fs
(10)
式中:ζ为附加摩擦阻力系数;Fmimax为起重机受偏斜侧向力一侧车轮受到的最大总轮压;λ为偏斜侧向力系数。

图6 双轨高低差示意
(3)当大车沿y方向运动且有风载时
当大车沿y方向运动且有风载时,其工况为:小车位于主梁跨中,吊重离地、满载悬挂于小车上,起升机构和小车运行机构静止,大车完成启动、加速、匀速运行、制动等运动过程,其载荷分析如图7所示。
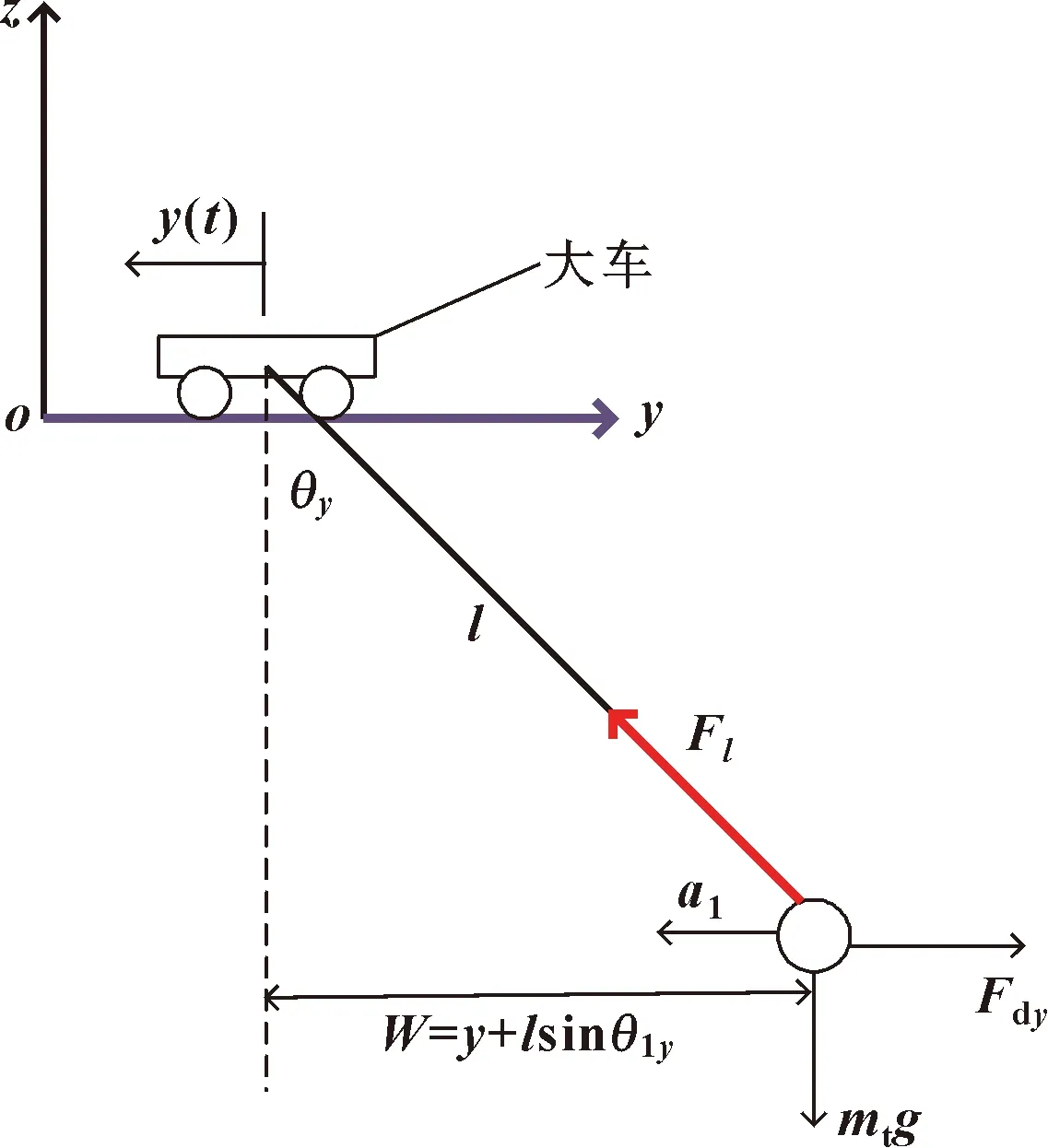
图7 大车运行机构受力
对起重机运动过程进行三维动力学分析,以大车位移方向(向左为正方向)为y方向构建坐标系,由此得到大车系统在运动过程中的动力学微分方程为
(11)
式中:m2为大车质量;Fy为大车驱动力;f为大车车轮组与导轨之间的摩擦力;Fdy为y方向风载;Fz为附加阻力。
以起吊重物为研究对象进行分析:
(12)
式中:θy为大车运动过程中起升重物与竖直方向的夹角,由式(10)(11)可解得:
(13)
式中:大车车轮组与导轨之间的摩擦力f可表示为
f=(Flcosθy+m2g)μ
(14)
式中:μ为大车车轮组与轨道之间的动摩擦因数。则式(13)可计算得:
(15)
根据起升重物在竖直方向载荷分析可知:
(16)
将式(4)(9)(16)代入式(15)得:
(17)
对式(17)进行整理得:
(18)
综上可得y方向摆角为
(19)
3 负载摆角三维仿真模型
若要对桥起负载的防摇摆问题进行理论研究并在后文中对防摆效果进行仿真验证,其结果则完全依赖于上述所建立的基于拉格朗日方程的非线性动力学方程。通常情况下,对于用数学表达式所描述的系统模型,用Simulink对数学微分方程进行仿真,能够得到更加真实的摆角仿真曲线。


表2 起重机参数


图8 Simulink仿真y摆角模型
3.1 驱动力大小对摆角的影响
如图9所示,通过改变Signal Builder模块中驱动力的波形将驱动力大小设置3 000 N,0~10 s时,Fy呈线性增加趋势,10~20 s驱动力保持不变,20~30 s驱动力大小呈线性减少趋势。假设没有风载的干扰,对模型进行仿真分析,得到如图10所示的同一驱动力Fy在不同作用时间下的摆角-时间曲线:0~5 s起重机大车是缓慢加速阶段,吊重摆动幅度一般;5 s后起重机大车以一定的速度保持继续加速,吊重摆角越来越大;20 s后,驱动力保持不变的情况下,由于惯性,吊重摆角依然在增加,但是摆角增速下降,这就为消摆措施的介入提供了时间差。由此可知增加驱动力大小对起重机摆动有一定的促进作用,即使驱动力在减小,由于惯性作用,吊重摆角依然会增大一段时间。

图9 驱动力作用波形 图10 不同驱动力作用时间下吊重摆角-时间曲线
3.2 风载对摆角的影响
在桥式起重机工作过程中,风载的存在势必会影响负载摆动。为了研究风载大小对摆角的影响,此实验在保持其他参数不变的情况下,仿真起重机在0~14 m/s风速下的摆角-风速的关系,得到如图11所示的摆角-风速曲线。可知:风速为0~4 m/s时,比较增速相对缓慢;4 m/s之后,摆角随着风速的增长持续增大,且摆角增速也在上升。这是由于惯性以及风速的双重影响导致的,摆角达到0.47 rad≈27°,此时对应的风速为12~13 m/s,对应风力约为6级。根据相关文献得知:在风力达到6级时,桥式起重机需停止作业。因此,风载对起重机负载摆动的影响不可忽略。

图11 起重机摆角与风载速度的关系
3.3 吊重质量对吊重摆角影响
针对吊重质量对吊重摇摆的影响,仿真条件设置其他参数不变,驱动力取3 000 N,风速取4 m/s,对模型进行仿真分析,得到吊重的摆角与和质量的关系,如图12所示。可知:随着吊重质量的增加,其吊重摇摆角度越小,初始吊重质量最小,其摆角幅度最大。这是由于当驱动力F一定时,吊重质量mt越大,则负载加速度a越小,吊重的摆角也越小。由此可得:在一定条件下负载质量对负载摆动幅度是有影响的。

图12 起重机摆角与负载质量的关系
4 结束语
在桥式起重机的一个作业流程基础上,建立起重机三维模型,根据起重机摆角在空间的状态,将它分解为大小车2个移动方向的分量,并对分量进行建模分析。采用牛顿第二定律建模方法将驱动力作用阶段、风载及吊重质量等因素考虑到模型内,仿真分析驱动力、风载方向对负载摆角的影响并得出相关摆角曲线。研究结果表明:初始摆角不可忽略,起重机的加减速度会加大负载摆动幅度,同时风载的存在以及方向对吊重的摇摆产生了一定的影响。该成果可以为后续进行起重机减摇、防摇研究提供理论依据,为提高起重机的工作效率和安全性提供理论基础。

