自适应多智能体算法优化深度网络的列车智能驾驶

徐凯，涂永超，徐文轩，吴仕勋

(1. 重庆交通大学 信息科学与工程学院，重庆 400074；2. 重庆大学 电气工程学院，重庆 400044)

列车自动驾驶ATO系统利用车载固化信息和地面通信实现对列车牵引、制动的控制，可使列车处于更佳的运行状态，提供更优的区间运行模式，提高旅客舒适度、行车密度和准点率[1]。列车控制算法是列车自动驾驶ATO系统的核心技术，将其研究分为两方面：一方面是ATO控制曲线的生成与优化，另一方面则是对生成速度曲线的跟踪控制。随着对列车多目标速度优化曲线研究的深入，如将粒子群优化算法与布谷鸟搜索相结合[2]，差分进化算法和非支配排序遗传算法相结合[3]等智能算法被广泛应用于列车多目标的智能驾驶中；在速度曲线跟踪控制方面，提出了基于分数阶PID的控制方法[1]以及列车自动驾驶非线性模型预测控制算法[4]。优秀司机的驾驶策略在能耗和舒适度上的表现比ATO更为优越[5]，对此，冷勇林等[6-7]结合专家系统，开发在线优化算法实现列车智能驾驶。将列车优秀驾驶员操纵数据称为“专家知识”，目前，它们尚处于“只存不用”的状态。倘若采用数据挖掘和机器学习的方法对“专家知识”充分利用，从海量数据中自动地发现隐藏于其中的规律性信息，将优秀司机驾驶策略应用于列车智能驾驶中，这不失为一种可行实用的方法。以上专家知识和经验，可从设计资料、列车运行监控装置LKJ、列车控制与管理系统TCMS设备上获取。基于数据驱动的机器学习方法是实现列车智能驾驶的常用手段。HUANG等[8]结合随机森林和支持向量机2种机器学习方法实现列车自动驾驶。李国华等[9-10]采用集成随机森林和CART等算法挖掘优秀驾驶数据。朱宇清[11]则提出一种BP浅层神经网络学习的货运列车控制方法。现有的优秀驾驶员操控模式学习方式，大多采用传统机器学习和浅层神经网络方法。在面对海量列车运行数据时，其特征表达不强、学习能力不足，不能全面反映列车运行状态，致使列车操控和预测精度不佳。因此，引入基于大数据的深度学习网络，从列车状态和环境中挖掘出所隐含的信息，并泛化出对未知状态的适应能力，用以实现列车智能驾驶。在深度学习网络中，卷积神经网络CNN的卷积运算特性决定其适用于处理具有网格状结构数据，它对于局部操作有很强的抽象表征能力，已广泛用于计算机视觉、语音和自然语言处理等各领域。对列车运行控制而言，其本质是一系列具有时间属性的档位和速度组合，而长短期记忆神经网络LSTM具有时序性特点，特别适用于对列车运行特征的表达。然而LSTM的结构设计涉及到网络的层数和节点数，属于超平面优化问题。目前通常依靠领域专家的经验知识，采用人为设定网络结构，具有随机性和盲目性[12]。若层数和节点数设计过少，则网络学习能力有限；若层数和节点数设计过多，则网络将过拟合，泛化能力较差。此外，LSTM超参数众多，是在一个维度极高的空间内，其优化是个非凸优化问题。非凸优化的主要难点是如何选择初始化参数和逃离局部最优点[13]。其中，对参数初值的选取十分关键，直接影响网络优化效率和泛化能力。然而在深度学习中最常用的Adam算法却难以解决上述问题，并在某些情况下可能不收敛。同时，朱海楠[14]构建深度神经网络对列车驾驶策略进行特征学习，所使用的网络仅针对单一回归学习任务，不能全面预测列车运行状态。李国华等[9]也分别使用4个模型来实现4个不同的任务，这仅属于单任务学习。而此处列车输出控制包括用于列车档位操纵的分类任务，同时还包括列车档位运行时间和速度预测的回归任务，它涉及到多个决策任务。若采用单任务学习方式，需要多个神经网络，不仅设计繁杂，信息冗余而且训练耗时。倘若仅用一个LSTM网络实现多任务学习，利用任务间的关联性来相互促进学习，不仅简化网络设计，且所得到的多任务学习网络比单任务具有更好的泛化效果[15]。但在多任务学习过程中，如何合理地处理不同任务之间的共性与差异，采用恰当的学习机制需要进一步地探讨和研究。因此，针对上述2个问题，本文做了以下两方面的工作，通过实验验证了所提模型的优越性和鲁棒性。第一，LSTM结构和超参数的初始化设计。在利用深度学习实现列车智能驾驶时，需要从深度网络类型和结构，以及优化算法等几方面充分考虑。具体地，在遗传算法GA优化LSTM结构基础上，结合多种群协同进化方式，提出一种新的自适应多种群链式多智能体算法(Adaptive Multi-Population Chainlike Multi-Agent，AMPCMA)，用以对网络权值和阈值等参数进行初步寻优。从而解决了LSTM结构设计盲目和参数初始化的困难。第二，实现了档位分类、档位操纵时间和速度预测回归的多任务学习。通过设计有效的多任务学习机制，即共享LSTM网络输入特征、网络底层模块，并采用Adam算法对各特定任务层的参数精细优化，将任务共性与个性学习有机结合，实现了精准、有效的列车多任务决策。

1 智能计算分步优化的LSTM模型

1.1 LSTM神经网络

图1所示为LSTM单元结构。

LSTM引入了遗忘门、输入门和输出门，分别决定信息的遗忘、保留和输出程度。其中各个门涉及到的计算公式如下。

式中：ft,it,ot分别为t时刻遗忘门、输入门和输出门的输出；c"t，ct，ht分别为t时刻候选记忆单元，记忆单元和隐含层的状态；Wf，Wi，Wo，Wc分别为遗忘门，输入门，输出门及候选记忆单元的权重矩阵；bf，bi，bo，bc分别为其对应偏置项；xt为t时刻的输入；[ht-1，xt]为2个向量的拼接；σ表示激活函数sigmoid，⊙表示向量元素乘积。

由图1可见，LSTM网络中的权重W=[Wf，Wi，Wo，Wc]和阈值b=[bf，bi，bo，bc]等参数通常是随机赋初值，然后利用Adam等算法进行优化。

1.2 自适应多种群链式多智能体算法(AMPCMA)

1.2.1 链式多智能体

智能体能够感知环境，相互通信，具有智能思维与智能行为。一个智能体代表问题的一个解。图2所示为链式多智能体结构，每个圆圈为一个智能体，依次相联为封闭的链式结构，形成一个智能体链表。链表上每个智能体都有左右2个邻居为其邻域环境。所有智能体的邻域共同构成该链表的局部生存环境。每个智能体通过竞争，交叉，变异以及自学习完成进化。链式结构的引入，缩小了智能体竞争范围，加快算法比较速度。图中，i=1，2，…，L为智能体在链表中的位置，L为链表规模。

1.2.2 AMPCMA进化框架

吴亚丽等[16]提出了一种链式多种群多智能体(CMPMA)算法，它在高维问题优化上表现出良好性能。然而，该算法所设计的链表规模是固定的，是一种静态链表，从而降低了算法的灵活性和自适应性。与其不同的是，本文所提出的AMPCMA算法能在进化过程中根据各小种群的贡献程度，自适应地调整小种群链表规模，让其成为一个可伸缩的“弹性”链表；此外，文献[16]中仅采用测试函数验证其性能指标，而未对深度神经网络的结构和参数配置进行寻优，更没结合实际工程应用，降低了问题研究的深度和实用性。

图3所示为本文所提AMPCMA算法的进化框架，具体思路如下：

1) 多种群协同进化。一个多智能体链表形成一个小种群。多个小种群协同进化，在全局寻优中，以恰当的通信周期，实现种群间的信息交互。

2) 全局寻优。各小种群链表上的多个智能体进行竞争，交叉和变异，实现自我更新。根据各个智能体链表的优劣，自适应地调整链表的规模，即将优质链表的规模扩大，缩小表现不佳的链表规模，让各小种群智能体链表“弹性化”。此外，种群间以适当通信周期进行信息交互，提高了种群多样性，避免算法陷入局部最优，提高全局收敛能力。

3) 局部寻优。每个小种群链表输出一个精英智能体，以特定方式生成局部小种群，经自学习得到最优智能体，此最优智能体经比较后输出。

1.2.3 AMPCMA具体实现

1) 多种群。由图3可见，Pi表示第i个小种群，i=1，2，…，n，n为种群个数。

2) 种群进化的4种规则

① 竞争。在智能体链表中，若某智能体Ai=(a1，a2，…，ak，…，ad)优于其邻域内的最好智能体Hi=(h1，h2，…，hk，…，hd)，则保留Ai，否则生成新智能体取而代之。生成过程为：给 定 占 据 概 率Ps，对A′i中 每 一 维 变 量a′k，若U(0，1)＜Ps，则

否则，

式中：k=1，2，…，d，d为智能体维度；U(-1，1)为(-1,1)间均匀分布的一个实数；xkmax和xkmin分别为第k维变量ak取值上下限；r1和r2为[0,1)间均匀分布的随机数。

② 交叉。每个智能体以概率Pc与链表中其余一个智能体随机交叉，产生新智能体取代当前智能体，采用单点交叉方式。

③ 变异。某智能体Ai=(a1，a2，…，ak，…，ad)的每一维变量ak，以概率Pm变异，得到新智能体Mi=(m1，m2，…，mk，…，md)。其变异过程为：

④ 自学习。指在精英智能体附近生成一个局部小种群，然后对其实施竞争和变异操作，经演化后得到一个最优智能体。这个局部小种群初始时只有一个智能体Eij=(e1，e2，…，ek，…，ed)，Eij表示第i个小种群输出的精英智能体，在链表中对应的位置为j，i=1，2，…，n，n为种群个数，j=1，2，…，L，L为智能体链表规模。在精英智能体附近按式(10)生成新智能体

式中：xkmax和xkmin分别为第k维变量ek取值上下限，mR∈[0,1]表示局部搜索半径，U(1-mR，1+mR)为(1-mR，1+mR)间均匀分布的一个实数。

3) 小种群链表规模的自适应调整方法

在全局寻优中，针对文献[16]算法中小种群链表规模固定不变，将造成算法性能下降的问题，这里采用自适应、动态调整链表规模的方式来解决。每次进化时，经过竞争、交叉和变异后，将产生的新智能体链表送至小种群规模调整控制模块。该模块根据各小种群的贡献率，在保持总智能体数量不变的条件下，动态调整各小种群链表规模，让各链表具备“弹性”伸缩的功能。具体的调整过程如下。

首先，按式(11)计算每个智能体k的适应度fk，其中e为网络3个输出量的误差总和。

按式(12)，计算第i个种群平均适应度Fi。

式中：li表示小种群Pi调整前的链表规模。

依据式(13)，计算出每个小种群的贡献率τi。

式中：n是小种群的数目。

然后，将各小种群的贡献率τi从大到小排序，按式(14)计算各小种群链表Pi调整后的规模δi。

式中：i=1，…，n，n为种群数目，N为智能体总数。

最后，完成对链表的伸缩调整。根据式(15)，判断各个小种群所增加或者减少智能体的数目Δi。

对链表的伸缩调整，可分以下3种情形：

1) 若Δi>0，则该小种群链表Pi需增加智能体，即拉伸。将该链表上的原有智能体按适应度从大到小排序，由大到小克隆前Δi个智能体加入链表中。

2) Δi=0，则该小种群链表Pi无需改变。

3) 若Δi<0，则该小种群链表Pi需减少智能体，即压缩。将该链表上的智能体按适应度从大到小排序，由小到大逐一删除后|Δi|个智能体。

另外，为避免某一种小种群链表强占优于其余小种群链表，调整时需遵循以下2个原则：① 小种群链表最大规模的上限增至初始规模的80%；② 小种群最小规模的下限减至初始规模的30%。

4) 种群之间的信息交互操作

每当算法演化一定代数时，随机选取2个种群Pi和Pj进行交互，即用种群Pi的历代种群所产生的最优智能体取代Pj种群中较差的智能体。

1.3 多任务学习实现

图4所示为本文所采取的学习机制。

这里采用硬参数共享的多任务学习机制来实现列车操控与预测。即在所有任务的底层中共享部分参数，在特定任务的顶层中使用各自任务的独有参数。硬参数共享网络通过共享输入层和LSTM隐层来学习特征表示，在输出端为各任务设计单独的分类、回归器。这种硬参数共享机制适用于各任务相关性较高的场景，提高了网络的泛化能力[17]，因此可将其用于列车智能驾驶。

在此多任务学习机制中，对网络参数的优化分为2个阶段。第1阶段是参数的初值预置，即利用AMPCMA算法对网络权值和阈值等参数进行初步寻优，将3种任务的误差总和作为网络训练目标，对多任务共性进行学习；第2阶段是参数的精细优化，即针对不同任务的个性，采用Adam算法对各特定任务层参数精细优化，将各任务的误差作为网络训练目标，分别对单任务的个性进行学习。通过以上方式，最终实现多任务共性和个性学习的有机结合，改善网络预测效果。

1.4 基于智能计算分步优化LSTM算法流程

首先，神经网络结构决定其信息处理能力，而网络结构一直是依靠领域专家的经验设计，这种人工设定方式具有随机性和盲目性。其次，神经网络参数的优化算法众多，其中Adam优势明显，在深度学习中使用较多。而本文优化的参数有1 747个，这是一个维度极高的非凸优化空间，若参数初值选择不当，将影响网络优化效率和泛化能力，而常用的Adam算法却难以解决上述问题。

因此，这里分步骤、分阶段并结合多智能算法优化LSTM网络。第1步采用GA优化网络结构；第2步利用AMPCMA和Adam算法优化参数。图5所示为其流程图。

2 仿真实验及分析

列车运行两目标优化就是在满足安全、平稳和精确停车等条件下，做到让列车运行时间短且能耗低。首先从列车运行监控装置、控制与管理系统获取重庆轨道3号线郑家院子到唐家院线路的1 440条司机驾驶曲线数据。然后将驾驶数据的能耗和时间在两维坐标轴上进行Pareto支配，剔除被支配解，再经拥挤距离裁剪得到均匀分布的147条驾驶曲线数据，将其定义为优秀驾驶员数据。接着用随机森林算法筛选出15个优质输入特征，包括线路、列车、列车运营和运行参数，见表1。

表1 LSTM网络输入特征Table 1 Input features of LSTM network

2.1 参数设置

1) 线路和列车参数。其参数如表2。

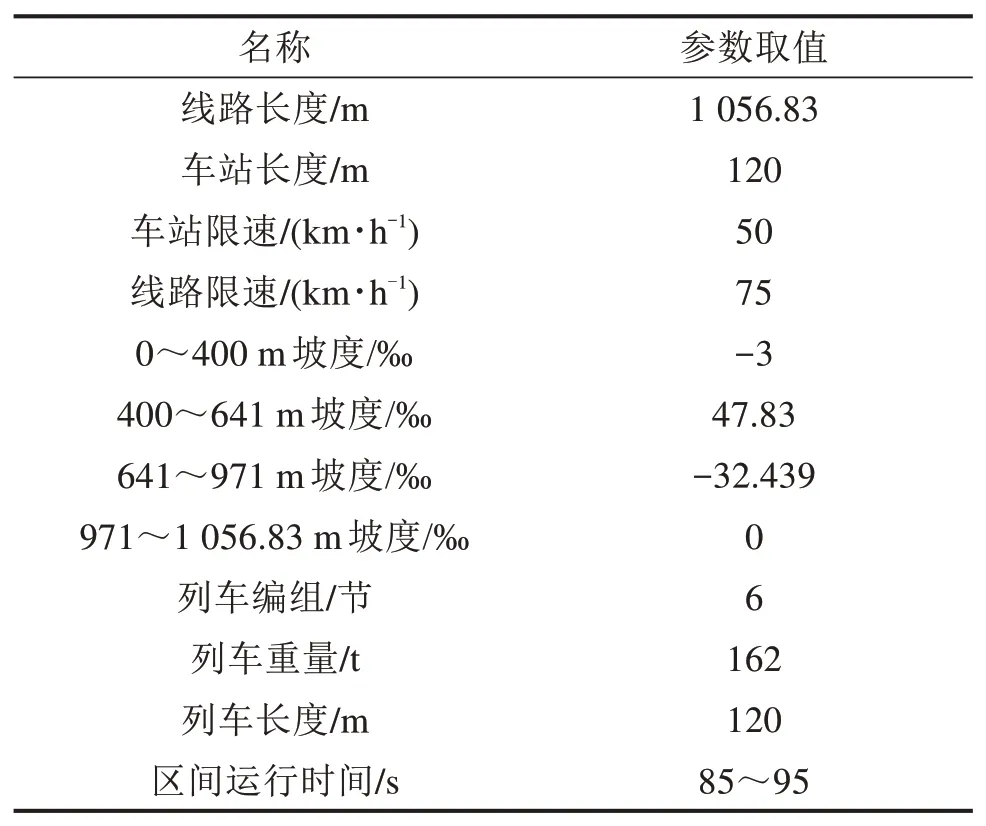
表2 线路和列车参数Table 2 Line and train parameters

2) 列车操纵档位、加速度值。列车档位共分8档，包括+3，+2，+1这3个牵引档，加速度分别为0.8，0.4，0.2 m/s2；0这个惰行档，加速度为0；-1，-2，-3，-4这4个制动档位，加速度分别为-0.2，-0.4，-0.6，-0.8 m/s2。此外，列车输入控制序列数为7。

3) 算法参数。GA中，网络隐含层及节点数量范围分别设为[1,4]和[6,15]，最大迭代次数100。AMPCMA中，有5个小种群，每个小种群有10个智能体，最大迭代次数80，信息交互周期为10代，自学习中进化代数为10，局部进化的链表规模为5，占据概率0.5，交叉概率0.48，变异概率0.08。

2.2 网络评价指标

1) 正确率acc。

该值越大，表示档位操纵正确率越高。

2) 交叉熵损失J。

式中：n为样本数；c为类别数；是第i个样本第k类标签值；表示第i个样本预测为第k类标签值的概率。J越小，档位输出误差越小。

3) 均方误差MSE。

4) 平均绝对误差MAE。

MSE和MAE 2个指标中，n为样本数，yi和y′i分别为真实和预测值。它们均用于评价列车档位运行时间和列车速度预测误差，其值越小，网络预测越准确。

2.3 深度模型结构的确定与性能分析

本节通过实验确定LSTM网络结构，在此基础上采用不同算法优化网络参数，以验证所提模型的优越性，并进一步验证该模型的鲁棒性。

1) LSTM网络结构的优化

采用GA优化LSTM结构，图6为优化过程。其中图6(a)为LSTM隐含层数量优化过程：依次淘汰的是1，4和3个隐含层，当迭代至65次时，稳定在2个隐含层。究其原因，较少隐含层不能充分表达网络特征；而较多隐含层则对数据特征表达过度。最终确定的结构为2个隐含层，其节点数依次为10和8。图6(b)为网络损失值变化曲线，其中网络损失值是LSTM网络3个输出的损失值总和，其值随着迭代次数增加而不断下降，最终稳定于0.34。

2) AMPCMA-LSTM模型优越性验证

针对前言所提问题，在前述LSTM结构基础上，采用AMPCMA和Adam分阶段、粗与细学习相结合的方式全面优化网络参数。AMPCMA具有良好的全局搜索能力，旨在寻找网络最优初始参数，使其收敛到一个泛化能力强的全局最优解。因此，先用AMPCMA对参数进行预训练初始化，再采用Adam对参数精调。该寻优方式取代了原有参数随机赋初值训练方法，降低了网络调参难度，优质的初始参数加快了网络训练和收敛速度，提高了网络性能。

基于上述分析，可得到用于列车精准操控和预测的AMPCMA-LSTM模型。为验证该模型的优越性，将其分别与前馈神经网络，传统机器学习方法，深度LSTM网络以及经典的PSO和GA优化的LSTM网络进行对比分析，其结果见表3。

表3 不同模型各评价指标统计结果对比Table 3 Statistical results comparison of various evaluation indicators of different models

由表3明显看出，BP与MLP的各项指标都较差。这是因为前馈网络无记忆功能，难以表达时序特征，从而预测效果不佳；传统学习方法SVM和SVR则分别用于分类和回归，由于这2种方法指向性更强，其MSE和MAE指标比前馈网络有所改善。

其次，除列车速度的MSE和MAE指标外，LSTM，PSO-LSTM和GA-LSTM的其余指标均优于前馈网络和传统机器学习。这是因为LSTM具有深度和时序记忆特点，能全面、动态学习驾驶数据，从而多项指标均有较大改善；此外，引入PSO和GA初步搜索LSTM参数，各项指标又得到进一步改善。

特别地，在表3所有模型中，AMPCMALSTM所获得的各项性能指标均为最佳。其中列车档位操纵正确率是最为重要的指标，所提模型比性能最差的BP提高了13.184%，比性能很好的GA-LSTM也能提高1.046%。上述实验验证了所提模型的优越性，能实现更精准的列车操控和预测。

虽然所提模型比前馈网络和传统机器学习方法耗时长，但却是3种不同智能算法优化LSTM用时最少的。用较长训练耗时换取各项性能指标大幅改善是合理的，这符合算法改进的基本准则[18]。并且，可通过多CPU并行处理的方式来解决训练时长的问题。

3) AMPCMA-LSTM模型鲁棒性验证

前述实验是列车在操控序列数为7的情况下进行的。实际上列车在自动驾驶中还存在多种工况序列。因城轨交通站间距离较短，列车在行驶中工况转换点不宜过多。为验证AMPCMA-LSTM模型的鲁棒性，采用列车操控序列数分别为4，5，6和7下的数据进行实验。在4种操控序列下，将算法分别独立运行30次，统计对比各评价指标，其结果见图7。

由图7(a)和7(b)可见，随着操控序列长度的增加，交叉熵损失J逐渐变大，其档位正确率也随之下降，但始终稳定在94.62%～95.51%，变化幅度在1%的微小范围内；由图7(c)和7(d)知，档位运行时间、速度预测误差的MSE和MAE 2项指标均在小范围变内化，趋势平缓。该实验证明所提模型在不同操控序列下具有良好的适应性和稳定性。

图8所示为4种操控序列下的档位值及其速度曲线。在不同长度的操控序列下，使用所提出的模型，列车操纵档位预测和真实值间仅有少许出入，速度预测与真实值的吻合程度较高；其次，从图8(d)和8(d′)还可看出，随着操控序列长度的增加，操控次数变多，操控错误概率也随之增加，这是一种必然现象。

3 结论

1) 从自动化深度学习的角度出发，重点采用无梯度搜索方法，分步骤、分阶段并结合多种智能算法优化LSTM网络结构和参数，进一步提高列车操控和预测精度。所提出的AMPCMA-LSTM模型与经典及改进的学习方法相比，档位操纵精度提升至94.627%，档位运行时间和列车速度的MSE值分别降至0.002 43和0.003 42，具有明显的优越性，并在不同操控序列下，对应各指标变化微小，表现出良好的适应性和鲁棒性。

2) 通过有效的多任务学习机制，即共享网络输入特征，网络底层模块以及优化算法等知识，将任务共性与个性学习有机结合，所提出的模型能实现列车档位、档位操纵时间以及速度的多任务决策，从而更加全面地掌握列车运行状态，实现更为精准的列车智能驾驶。