TR08磁浮列车辐射气动噪声特征的仿真研究

吴雨薇 ，高建勇 ，杨志刚

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 轨道交通安全关键技术国际合作联合实验室，湖南 长沙 410075；3. 轨道交通列车安全保障技术国家地方联合工程研究中心，湖南 长沙 410075)

近年来，高速列车快速发展，成为人们出行的主要交通工具，但当速度提升至400～600 km/h区间，高速列车将受到轮轨系统以及弓网受流条件限制，为了提高交通运输能力以适应经济发展和民生的需要，高速磁浮列车逐渐成为关注热点[1-3]。早在上世纪80～90年代，德国已开展了常导高速磁悬浮技术的研发和应用工作[4]；2009年，德国TR09磁浮列车试验速度达到550 km/h[5]；日本对超导磁浮进行了系统研究，主要有MLU和L系列列车，其中L0超导磁悬浮列车在2015年试验速度达到603 km/h[6]；2003年，我国引进德国技术建造的上海磁悬浮列车专线[7]，运营速度430 km/h，这也是当今世界唯一运营的高速磁悬浮列车。十三五期间，我国启动了600 km/h 高速磁悬浮列车的国家级重点科研项目研发。2019年5月23日，我国600 km/h高速磁浮实验样车在青岛下线[8]，这表明我国高速磁悬浮列车技术已经取得突破性进展。高速磁浮列车主要噪声源为气动噪声。随着车速的提升，气动噪声能量迅速增加(与车速的6～8次方成正比)[9]；车速超过0.3马赫数，列车周围、尤其是尾部/尾流区的四极子源逐渐显现[10]。急需探明其气动发声机理和气动噪声辐射特征。然而目前公开的研究多为线路噪声数据。由TR08的德国试验线噪声数据[11]可知，400 km/h时，其25 m标准点最大辐射噪声达到了91 dBA；600 km/h时的试验外推噪声值约100 dBA。我国上海磁浮线路噪声试验测得列车以430 km/h通过时，距离轨道中心线35 m，高出地面1.6 m位置的A计权声压级为96 dBA[12]。可见高速磁浮列车的气动噪声问题不容忽视。现阶段针对600 km/h高速磁浮列车模型的试验研究条件是相对缺失的，数值仿真是可行的主要研究手段。本文借助高速列车气动噪声仿真研究的相关经验[13-15]，采用大涡模拟及K-FWH方法，精细化研究TR08磁浮列车的近壁面气动发声特征及远场辐射气动噪声的变化规律，分析不同速度级条件下气动发声的偶极子和四极子效应。本文研究成果可为高速磁浮列车气动声学优化设计提供参考。

1 TR08辐射噪声试验数据分析

为描述高速磁浮列车辐射声压级与速度对数值之间的关联关系，利用TR08试验数据对二者进行二次拟合，对应的拟合曲线公式如下：

式中：v为速度；v0为基准速度。

将拟合公式计算得到的拟合值与试验值进行对比，如表1所示。由表1可见，拟合值与试验值相差在0.5 dBA以内，表明式(1)具有较高的拟合度；利用该公式估算得到在600 km/h速度级下，5车编组的TR08列车辐射声压级为99.6 dBA。

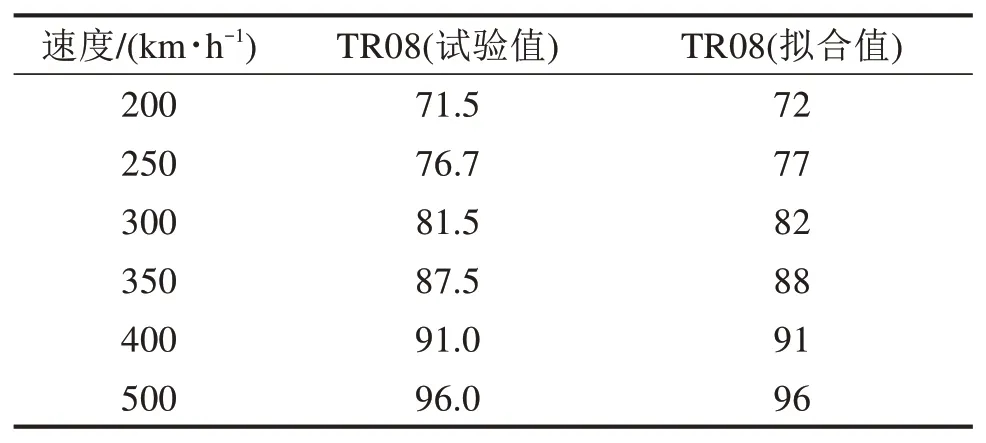
表 1 德国线路测试数据-最大辐射噪声级[11]Table 1 German line test data-maximum radiated noise level dBA

2 流场扰动特征的仿真分析

2.1 几何模型及流场计算设置

本文采用1∶8缩比尺度的简化TR08列车模型，不考虑列车顶部天线。如图1所示，从上游至下游将列车车体主要分为头车流线型、头车、中车、尾车及尾车流线型几部分。为简化计算，模型位于计算域中间，仿真过程不计入地面边界；最后在辐射噪声结果中计入地面效应修正，来模拟磁浮列车在高架的运营情况。计算域大小为460 m×92 m×96 m(全尺寸)。在x方向上，计算域入口ABCD距离车头鼻尖点115 m，尾车鼻尖点距离计算域出口265 m，如图2所示。

计算域入口ABCD和计算域出口EFGH均采用压力远场边界条件，流域4个侧面均给定对称边界条件，使该面法向速度为0，保证流场发展的同时消除壁面对流场的影响，列车模型表面设定为无滑移边界条件。磁浮列车轨道设定为滑移固壁边界条件，滑移速度与来流速度一致。采用三维可压缩理想气体模型。

考虑到来流马赫数大于0.3，空气可压效应明显。因此，稳态流场计算选取基于密度基的隐式求解方法，采用SSTk-ω湍流模型开展数值仿真，对流项和耗散项均采用2阶迎风格式进行离散。随后，开展LES计算，采用基于Smagorinsky-Lilly的LES模型，压力和速度场耦合采用Coupled算法；采用有界2阶隐式格式对时间导数进行离散，有界中心差分用于离散动量方程。非定常计算时间步长为5×10-5s，每时间步长内迭代30次，共计算10 000个时间步，确保气流有足够的时间通过整个计算域。

2.2 网格划分和网格质量

图3为列车网格示意图。全局采用非结构四面体网格划分，网格规模约2.1亿。采用分区控制加密方法：全尺寸条件下，流线型车头采用30 mm网格尺度，头车尾车采用40 mm网格尺度，中车采用50 mm网格尺度；在车尾区设置3层嵌套加密区，其网格尺度分别为100，200和400 mm。为描述列车表面偶极子噪声源，在车体表面设置15层附面层网格，第1层网格厚度为0.1 mm，增长率为1.2。车体表面y+值基本在1左右，表面网格尺寸能满足大涡模拟的基本要求。

为验证网格无关性，调整3层加密区网格尺寸得粗网格和细网格列车模型，如表2所示，网格量分别为1.0亿、2.1亿和2.6亿。3套网格得到的稳态气动阻力系数分别为0.357 1，0.311 2和0.310 1，计算网格和细网格整车阻力系数之间的偏差小于1.0%，可认为本文模型满足网格无关性要求。

表2 网格尺度和气动阻力系数Cd(全尺寸)Table 2 Mesh size and aerodynamic drag force coefficient Cd (full scale)

2.3 近壁面流场(扰动)分析

在400～600 km/h速度级下，列车流场特征类似，因此本节主要以600 km/h速度级下流场结果对列车气动激扰特性进行分析。

图4为稳态计算输出的列车纵向对称面及头车、尾车表面压力云图。由图4可见，TR08列车高压区集中在头车/尾车流线型尖端附近；受流线型肩部位置气流分离影响，头车/尾车流线型肩部至头车/尾车抱轨呈现负压。

图5给出y=0 m截面，列车顶部附面层内部速度变化；数据提取高度为车顶上方0.04 m位置。由图5可见，在头、尾车流线型区域，速度幅值波动明显，在头车鼻尖点，速度下降到最低幅值，随后沿车体增长，在头车流线型肩部区域，速度幅值最大，在气流流经头车流线型肩部位置后，气流速度沿车身不断下降，直到尾车流线型肩部分离区域，速度幅值开始上升，在鼻尖点后，速度幅值出现上下波动，反映出不稳定的分离流动特征。

本文采用速度梯度张量第二不变量，即Q准则，识别列车周围的涡结构，来展示列车周围瞬态流场特征，Q准则表达式为

图6给出磁浮列车600 km/h速度级下列车周围空间涡结构云图。由图6可见，磁浮列车周围扰动涡结构主要集中分布在头、尾车流线型区及尾流区，主要体现为：1) 在头车流线型底部两侧，有少量条带状分离流扰动沿车体向后发展；2) 在头车流线型上表面，气流撞击头车鼻尖点沿车体向后发展，由于该区域流线型设计并不充分，会由于高压力梯度形成较强的不稳定扰动(由于没有较明显的流动分离，该区域仍然以偶极子源为主)；3) 在列车车身，主要是较低能级的湍流边界层脉动噪声；4) 在尾车流线型肩部，气流与车体分离，在该位置涡团聚集呈带状结构，并在尾流区域进一步发展成为向车体两侧翻转的强分离对涡结构，扰动传播距离超过了一节车体的长度。显然，分离尾涡结构特征是气动发声的一个关注焦点。随着速度增加，列车尾流区涡结构向后发展得更远。图7给出600 km/h速度级下尾流区涡结构，可见，从尾车流线型肩部开始出现明显的分离涡结构；在向后运动的过程中，涡结构不断破碎又融合，能级逐渐减弱。图8给出列车尾流区不同截面位置的涡量云图。其起点为尾车鼻尖点，向下游每隔1 m取一个截面。由图8可见，在尾车鼻尖点截面，涡量幅值最大，尾车流线型底部以及表面脱落的涡结构在该位置相互掺混；随着涡结构向下游发展，强涡量区域向两侧及下方扩展，涡量幅值随之减小。

3 声源声辐射分析

3.1 K-FWH积分方法及人工积分面设置

K-FWH方法是FRANCESCANTONIO[16]在传统FW-H方法的基础上利用Kirchhoff方法[17]的基本思想推导而来。传统的FW-H方法在计算空间四极子声源发声时需对整个计算域进行繁琐的体积分。K-FWH方法在计算域内建立包含主要声源扰动的虚拟可穿透的包络积分面，在积分面外，声辐射满足线性/拟线性传播规律。此时只需对虚拟积分面进行单极子和偶极子的面积分，即可得到积分面内所有声源的辐射贡献[18]。

虚拟积分面的设置应足够大，包含列车周围所有主要流场扰动源信息，从物理上避免声源信息的缺失；同时需要确保积分面内(包括车体表面)的扰动源信息能够无损传递到虚拟积分面上，尽量减少网格滤波损失，因此会对积分面内的网格提出更高的精度要求，导致计算量剧增。

根据上节对列车气动激扰特性的分析可知，列车尾流区气动激扰强烈，是最主要的四极子声源区，需在该区域考虑建立虚拟积分面。为明确列车尾流区扰动的主要区域，图9给出了纵向对称面涡量幅值变化。

由图9可见，尾流区的涡量幅值波动较大，在15 m之后，涡量波动迅速减小，在20 m之后，涡量幅值趋近于0，因此需将积分面尾端面设置在20 m之后；由于湍流边界层与车体分离之前，其内部四极子扰动基本不向外辐射噪声，主要体现为表面偶极子噪声，因此将积分面起始位置建立在尾车流线型肩部位置之前，确保积分面入口端面没有分离流扰动，积分面出口端面距离辐射观察点足够远，无质量穿透。为避免积分面端面的净质量穿透导致的虚假声源贡献问题，在下面的辐射计算中，忽略端面积分。

具体积分面设置如图10所示，积分面俯视呈现梯形、侧视呈现矩形特征。以车高H=4.2 m为特征长度，入口的上端面距离车顶0.3H，下端面距离轨道底面0.3H，侧面距离车体表面0.5H；积分区域沿轨道长度20H；出口高度1.6H，宽度3H。

3.2 表面偶极子源

可采用表面脉动压力时间梯度p"来描述列车表面偶极子声源强度，如式(2)所示，计算得到其能量时均值p"rms，并利用式(3)无量纲化：

式中：T为采样时间。

为进一步明确列车各部分偶极子声源能量贡献，利用式(4)可得到各部件等效声源声功率值，进而得到声源能量占比。表3为TR-08在400，500及600 km/h速度级下各部件偶极子声源能量占比。由表3可见，在不同速度级下，偶极子声源能量主要集中在尾车，其次是中车，头车区域占比最小。

表3 车体各部件偶极子声源能量占比Table 3 Energy proportion of dipole sound source of train components

3.3 远场辐射气动噪声和四极子贡献

在标准噪声测点位置(距离列车纵向对称面6.25H远，高出地面0.875H)布置32个噪声测点，在x方向上，第1个测点距离头车鼻尖点5H远，向下游每隔2.5H布置1个测点，列车位于测点3至测点11之间，具体如图12所示。由于磁悬浮采用“抱轨”形式，车底声能量不能向侧向传播，在本文远场噪声计算中不考虑车底抱轨内腔的发声。

对于测点1～测点32，从车体积分以及从局部外推积分面积分得到的远场辐射噪声如图13所示。由图13可见，随着速度级的增加，各个测点声压级随之增大，但声压级变化规律比较一致。在400，500和600 km/h速度级下，车体辐射噪声最大值分别为83.7，89.7和94.7 dBA；增加尾流区虚拟积分面后远场辐射噪声最大值分别是86.2，91.7和95.6 dBA。从对比来看，尾流区测点声压级明显上升，表明尾流区四极子声源的辐射贡献占比较大。

这里进一步给出辐射噪声最大测点(08测点)的频谱结果，如图14所示。由图14(a)可知，列车辐射噪声呈现宽峰特征，峰值频率位于600～800 Hz区间，这是车体表面随机脉动的偶极子源和尾涡共同作用的结果，随着速度的提升，峰值位置缓慢向高频迁移；在低于1 000 Hz的频段，随着速度的增加，频段内声压级随之增大；由图14(b)可见，在低频段，外推积分面声压级高于车体积分结果，这正反映了车尾分离导致的扰动能量转换以及尾涡区的低频扰动贡献；而高频部分相对较小，这可能是由于积分面内网格的滤波效应导致车体表面偶极子声能量向积分面传递时能量有所损失。

为研究远场辐射噪声偶极子声源及四极子声源能量贡献，利用式(5)可求得列车辐射声能量，利用式(6)求得四极子声源辐射能量占比，结果如表4所示。

由表4可知，在各速度级下，列车四极子声源辐射能量贡献均非常显著，随着速度的提升，四极子源辐射能量占比随之增大，在600 km/h时，四极子声源的平均辐射贡献能量占比达到约83%，这也反映了TR08车尾分离激扰作用剧烈，在该区域产生了较多的四极子声源。从车头、车尾、尾流区不同典型测点的结果来看，对于列车头部，偶极子和四极子贡献均显著(测点3)；车体中后部对应观测点，主要以偶极子噪声为主(测点8)；对于尾流区，主要以四极子贡献为主(测点16)。

表4 TR08声辐射能量占比Table 4 Proportion of sound radiation energy (TR08)

3.4 地面效应修正

由于高速磁悬浮列车一般在高架上运行，而本文仿真模型未考虑地面边界影响，当无需考虑地面边界与车体周围气流的相互耦合作用时，可只进行地面反射效应修正。

地面反射效应如图15所示，实际辐射噪声声能量为直接辐射声能量和地面反射声能量之和。

考虑列车和地面距离为h(m)，标准噪声测点位于列车侧向25 m远，利用镜像原理可以计算地面效应的修正值，对应高度h与修正值之间的关系见表5所示。

表 5 列车的辐射噪声修正值Table 5 Radiated noise correction value of train

德国TR08列车试验线高架高度约为10 m，采用上述地面效应修正对仿真结果进行修正，应在仿真结果最大值的基础上增加2.5 dBA。表6给出400～600 km/h速度级气动噪声标准值、仿真修正值和二者差值。其中400 ~500 km/h标准值为德国实车试验值，600 km/h标准值为采用式(1)得到的拟合值。

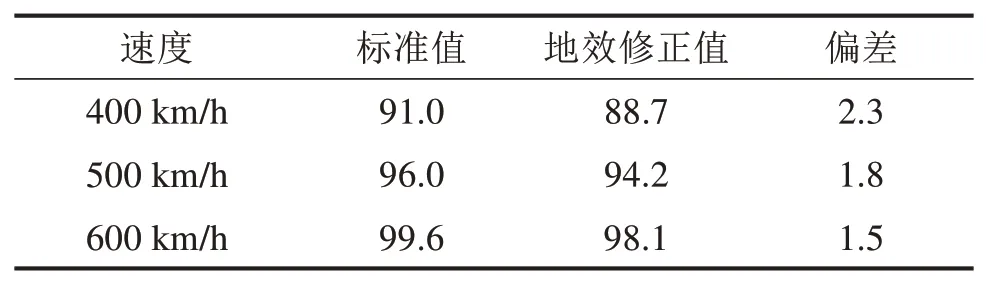
表 6 标准值和仿真修正结果对比Table 6 Comparison of standard value and simultaion correction value dBA

由表6可知，在400～600 km/h，修正结果均比标准值要小，差值最大约2.3 dBA。导致这一现象的原因可能是由于在修改列车模型时省略了天线，TR08列车顶部天线长约1 800 mm，高约500 mm，宽约250 mm，按照高速受电弓模型计算经验，不考虑天线会使总噪声结果减小1～2 dBA[19-21]。

4 结论

1) 磁浮列车车身平顺，主要发声源为附面层在尾车流线型区域与车体分离所引起的空间扰动。

2) 列车偶极子声源主要分布在尾车流线型底部及鼻尖点，四极子声源主要分布在尾流区域。

3) 当TR08磁浮列车运行速度超过400 km/h，四极子声源辐射能量将超过偶极子声源，占据主导地位，在400，500和600 km/h速度级下，四极子声源占比分别为70%，74%和83%。

4) 在对列车辐射噪声仿真结果进行地面修正后，与标准值吻合效果较好，但较标准值略小，可能是由于省略模型天线所导致。

本文构建的气动噪声仿真方法能较好地捕捉磁浮列车高速运行时所产生的四极子声源，对列车的气动声学特性有了进一步的了解，同时对TR08列车噪声优化设计具有借鉴意义。