基于随机规划的高铁列车超售策略分析
邓连波 ,许景 ,彭齐 ,胡心磊
(1. 中南大学 交通运输工程学院,湖南 长沙 410075;2. 中南大学 湖南省轨道交通大数据实验室,湖南 长沙 410075)
近年来,许多学者研究了收益管理策略在铁路领域的应用,但主要集中在需求预测、动态定价和席位分配等方面,而在航空领域已普遍运用的超售策略则鲜有涉及。超售策略是为了避免已购票旅客未乘车或退票所产生的损失,而采取售票数量多于列车能力的一种客票销售策略。通常情况下,高铁列车尽量避免无座票的存在。在不允许无座票存在的情况下,列车能力等同于定员(即实际席位能力)。但在允许少量无座票存在的特殊情况下,列车能力等于席位能力和允许销售的无座票限额之和。当超售数量过多时,会导致部分旅客被拒载,影响铁路部门声誉,产生拒载风险。超售数量过少时,乘车客流不足,列车能力不能充分利用,产生空座损失。因此,确定合适的超售数量在提高收益的同时可有效控制拒载风险,有利于实现铁路部门收益最大化和社会资源利用最大化。航空领域关于超售策略的研究分为静态方法和动态方法2类。在静态方法方面,BECKMANN等[1-2]较早地研究了超售优化模型,其理论成果对后续研究具有较强的实用价值。朱金福等[3]采用排队论模拟机票销售过程,给出舱位最优订座限制的决策方程。衡红军等[4]提出了考虑成行率和成行人数分布的2种超售数量计算模型。MOU等[5]建立了网络环境下的随机机会约束的整数规划超售模型。王航臣等[6]通过改进报童问题建立了超售数量优化模型,并采用蒙特卡洛方法验证。在动态方法方面,KOSTEN等[7-8]分别研究了连续时间和离散时间的超售模型。朱金福等[9-11]在研究中分别将旅客订票过程视作马尔可夫生灭过程和Poisson过程。陈敬光[12]从风险偏好的角度展开研究。ALAVI等[13]将最大化市场份额为超售策略的优化目标,采用动态规划求解。铁路行业超售问题的研究尚处于起步阶段。郭颂章[14]给出了最佳超售数量的简易近似算法。田志强等[15]综合考虑了列车开行的经济效益和社会效益,建立客运专线超售模型,并采用数值计算验证。单杏花[16]介绍了铁路超售的条件,给出铁路始发站超售控制模型,但未涉及具体的求解方法。潘跃等[17]用简单算例验证了超售的必要性和现实意义。结合上述分析可知,目前国内铁路行业的超售研究较少,且未提出较好的优化模型和求解算法。由于铁路与航空在运营上的巨大差别,航空领域的经验并不能直接应用于铁路领域,因此需要探索适合我国铁路发展的超售策略。在酒店、航空和铁路等领域中的收益管理和超售问题的研究中,通常采用show[4](或者show-up[12])和no-show来描述服务对象在预定后是否按计划入住或者乘车的状态。对于已购票的高铁列车客流,可分为旅客按时成功出行的乘车状态,以及旅客因主观原因放弃乘车或者因主客观原因错过列车的弃乘状态,分别对应一般超售问题的show和no-show状态。本文在不涉及超售的具体管理措施的条件下,对高铁列车超售优化问题及超售策略的效果进行研究。以某一乘车OD的全部客票作为销售对象,按列车能力的一定比例作为超售票额销售,从铁路收益最大和社会声誉的双重角度出发,以期望净收益最大为目标,将被拒载旅客的概率限定在一定范围内,提出考虑旅客弃乘行为随机性的非线性整数随机规划超售模型,并采用遗传算法求解。
1 高铁列车超售问题分析
1.1 问题假设
为研究高铁列车超售策略的规律,作如下假设。
1) 将不同席位种类的客票超售视作是可独立优化的问题,为此仅考虑单一席位种类下的超售问题。本文以高铁列车席位比例最大的二等座作为研究对象。
2) 旅客订票后只有乘车和弃乘2种状态。考虑到铁路当前客票销售政策,对弃乘旅客按照一定的退票费率收取退票费用。
3) 为简化起见,本文仅研究一定客票价格下的超售数量优化问题,未考虑其他收益管理手段的影响。同时,由于列车开行后大部分运营成本已经发生,因此可将其视作是常数,认为其与客流数量的变化无关,在优化问题中不予考虑。
4) 由于客运交通企业运营一般受到严格的监管,因此可认为决策者是风险中性的。
1.2 高铁列车超售问题描述
对所研究的乘车OD,列车能力为c,客票价格为f。在客票销售过程中,实际售票数量为m。在超售情况下,一般有m>c。已购票旅客中,因旅客自身原因放弃乘车的旅客数量,即弃乘人数为n,这些旅客可按照退票费率γ进行退票。
旅客弃乘受到很多不可控因素的影响,如行程改变和市内交通延误等,具有随机性。一位旅客在购票后只有乘车和弃乘2种状态,乘车和弃乘的概率服从二项分布。基于客流出行数据的统计分析,设每位旅客弃乘的概率为p,乘车的概率则为1-p。则n名旅客弃乘的概率pn可以表示为:
由于高铁列车能力较大,即使考虑一定的上座率,m仍然很大,而且p很小,可以用泊松分布近似代替二项分布。此时n名旅客弃乘的概率函数近似等于强度为参数λ=mp的泊松分布,因此pn也可以表示为:
采用超售策略后,除了客票销售收益和退票收益外,也可能会带来拒载风险和空座风险。当m-n>c时,由于列车能力数量不能满足实际乘车旅客需要,就会产生拒载风险,拒载一名旅客的铁路赔偿成本为d(单位拒载成本);反之,就会产生空座风险。
拒载风险和空座风险受超售数量和弃乘旅客数量的共同影响。过多的超售数量会给铁路的社会声誉带来负面影响,也会给旅客的出行带来不便。因此,铁路企业为了维护其社会声誉和企业形象等方面的原因,也要尽可能避免拒载现象的发生,需要对拒载概率pd进行控制,如将拒载现象的发生概率控制在某一个较小值α以内,称α为最大拒载概率。
超售策略所产生的各项收益和风险损失情况如图1所示。
2 高铁列车超售策略的随机规划
基于图1中m,c和n之间的关系,客票超售后,高铁列车的运营净收益如下:
《中华人民共和国城镇土地使用税暂行条例》[10]中明确规定:直接用于农、林、牧、渔业的生产用地免缴土地使用税。
由于弃乘人数是一个呈泊松分布的随机变量,因此可用期望净收益来表示超售策略下的运营净收益。
当n<m-c时,会发生拒载现象,拒载概率pd可按下式计算:
在实际售票过程中,超售数量不能无限增加,行业监管部门也会对超售数量予以限制。本文采用最大超售率β(超售票额占列车能力c的最高比值)作为超售数量的限制条件。
综上,基于最大拒载概率约束和最大超售率约束,以期望净收益最大为目标,可建立高铁列车超售数量优化的数学模型如下:
其中,式(6)是目标函数,式(7)是最大拒载概率约束,式(8)是最大超售率约束,式(9)是变量的整数约束;实际售票数量m是优化模型的决策变量,其对应的超售票额为m-c。
该模型是一个基于随机规划的非线性整数规划模型,约束条件和目标函数与随机变量p有关,直接求解其解析解很难获得。因此,本文采用具有全局寻优能力、高效实用的遗传算法求解。为方便运算,本文通过调用现有MATLAB遗传算法工具箱中ga函数进行求解。
3 客票超售策略分析
以广州南至深圳北G6205次列车为例,在其票额全部分配给广州南至深圳北乘车OD的条件下,优化确定其超售数量。该列车的列车能力和客票价格等参数如表1所示。
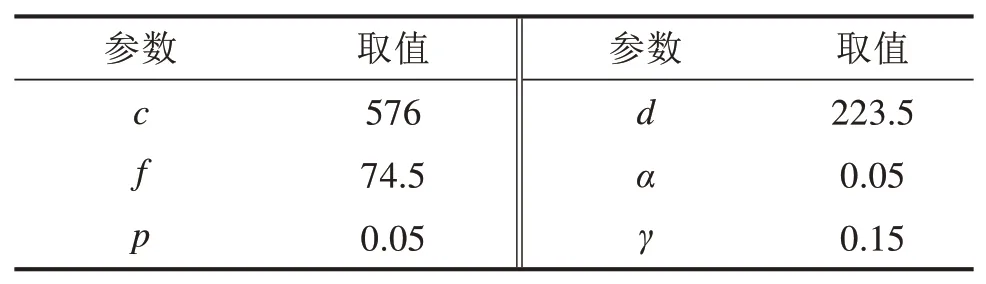
表1 算例参数取值Table 1 Parameter value in numerical instance
在实际客票销售过程中,超售数量一般控制在列车能力的5%~15%。因此本文取最大超售率β=0.15。实际售票数量m的取值范围为[0,c(1+β)],遗传算法中每个个体m采用二进制编码,采用长度为10的位串表示基因,即从“0 000 000 000”到“1 010 010 110”,对应整数区间[0,c(1+β)=662]。将目标函数作为个体适应度值。遗传算法的相关参数设置如下:种群规模为20,交叉概率为0.8,变异概率为0.08,最大迭代次数为60。
在不采取超售策略即m=c时,期望净收益为41 088元。在采取超售策略时,采用遗传算法求解,通过MATLAB计算可得实际售票数量为597,超售数量为21张,此时,期望净收益为42 559元。图2为期望净收益在优化过程的变化情况,证明该算法具有较快的收敛速度和较为准确的结果。实施超售策略后,该乘车OD的期望净收益增加了1 417元,提高3.58%。假定每日收益多增加1 417元,铁路部门的总收益一年可增加517 205元。
对模型和算法中的重要参数进行灵敏度分析,分别研究弃乘概率p,最大拒载概率α,最大超售率β和单位拒载成本d对实际售票数量m和期望净收益E的影响。
3.1 弃乘概率p
令p由0.01增加至0.2,分析期望净收益E和实际售票数量m的变化情况。从图3中可以看出,随着p的增大,为弥补逐渐增加的空座损失,超售数量不断增加,旅客被拒载的概率也在增大,对期望净收益产生负面影响,但由于弃乘旅客会带来退票收益,因此在能够弥补空座损失的条件下期望净收益整体上呈现波动上升的趋势,当p=0.15时,期望净收益获得最大值。此后,受到最大超售率的限制,实际售票数量达到最大值662后不再增加,弃乘人数继续增加所带来的空座损失无法被弥补,期望净收益急剧下降。
3.2 最大拒载概率α和最大超售率β
图4(a)为α由0.01增加至0.3时期望净收益E和实际售票数量m的变化情况,α的增大意味着允许更多的旅客被拒载。随着α的增加,实际售票数量和期望净收益相应增加,但在一定弃乘概率条件下,超售数量过多会造成高昂的拒载损失,因此期望净收益和实际售票数量不会无限制地增加,当α>0.21后,实际售票数量和期望净收益都不再变化。图4(b)为β由0.01增加至0.2时期望净收益E和实际售票数量m的变化情况,β的增大意味着允许售出更多的车票。随着β的增加,实际售票数量和期望净收益都有所上升。但超售率越高,铁路需承担的拒载成本越大,因此β继续增加时,实际售票数量和期望净收益都不再变化。从图4可以看出,控制α与β会对期望净收益和超售数量起到相似的影响作用。
3.3 单位拒载成本d
令d由票价的1倍增加至5倍,分析期望净收益E和实际售票数量m的变化情况。本文讨论2种情况。情形1:拒载数量受到约束(7)中最大拒载概率α的限制;情形2:松弛掉约束(7),对拒载数量不加以限制。
情形1和情形2中E和m的变化情况分别如图5(a)和5(b)所示。从图5(a)可以看出,随着d的增加,期望净收益越来越低,超售数量并未发生明显变化。这是因为当d较低,受到α和β的限制,不允许实际售票数量过多,以避免造成过多的旅客被拒载,当d过高时,为降低拒载赔偿成本,实际售票数量也不会增加。因此,最优实际售票数量始终保持597张,这也与图4中α=0.05和β=0.15时实际售票数量为597张一致。从图5(b)可以看出,由于松弛了α的限制,被拒载数量不再受到限制,在满足超售率的条件下,实际超售数量的多少由期望净收益驱动。随着d的增加,期望净收益和实际售票数量逐渐减小。d越低,超售产生的拒载损失越小,因此,实际售票数量越多,所获得的期望净收益越大。
4 结论
1) 合理的超售数量可以有效提高铁路收益,对给定算例列车收益提高约3.58%;
2) 随着旅客弃乘概率的加大,超售收益呈先升后降趋势,弃乘概率较大时采取超售策略会面临着较大的拒载风险;
3) 作为2种超售策略的控制条件,最大拒载概率和最大超售率对超售净收益和超售数量起到相似的影响作用;
4) 若加大企业对拒载旅客的补偿,会使超售策略面临较大的风险,超售数量和超售净收益均会呈下降趋势。
为研究高铁列车超售效果和超售策略规律,本文对问题进行了较大简化,针对单列车单OD的超售问题展开研究。后续研究还可对多列车情形下和多收益管理手段融合条件下的超售问题和高铁网络多OD竞争列车能力情况下的超售问题以及基于严格监管约束下运营风险偏好的高铁列车超售问题进行进一步的探索。

