基于图像识别的耐火材料破损率计算方法研究
刘亚径,王兴东,朱青友,刘 钊,雷付煜
(1. 武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2. 武汉科技大学省部共建耐火材料与冶金国家重点实验室,湖北 武汉,430081;3. 武汉科技大学计算机科学与技术学院,湖北 武汉,430065)
耐火材料是高温工业不可缺少的基础材料。以耐火材料为基材的热工设备炉衬在服役过程中频繁遭受温度急剧变化,其内部会产生热应力,当应力值超过其结构强度时将导致相应结构出现开裂、剥落甚至砌体崩裂,因此,抗热震性即抵抗温度急剧变化而不损伤的能力是衡量耐火材料使用性能的重要指标[1]。现行国家标准[2]以耐火材料在重复高温加热后急冷的循环条件下受热端面积破损率达到50%时所对应的循环次数k作为其抗热震性指标,其中材料受热端面的面积破损率由人工测定,因此,基于该标准所得检测结果受人为因素影响较大且不能体现材料破损过程特征,同时传统检测装置还存在耗时长、安全性差等不足。
近年来,机器视觉检测作为一种现代检测技术已逐渐应用于耐火材料性能检测领域[3],如李海华等[4]采用视觉检测技术对耐火砖进行了外形尺寸测量;程骏等[5]利用机器视觉并基于Hessian矩阵计算了耐火砖裂缝的尺寸,不过未深入进行耐火砖剥落区域识别及相应的面积破损率计算。利用机器视觉对材料裂缝和剥落等破损进行识别的方法主要有阈值分割、连通域特征、霍夫变换等[6],Lei等[7]结合无人机及数字图像处理技术提出了一种基于裂纹中心点的方法来检测桥梁结构的裂缝;罗佳等[8]基于自适应阈值和连通域标记的隧道裂缝提取方法对相关裂缝成功实施了粗定位和细提取;徐港等[9]报道了一种基于多种连通域特征的工程结构表面裂缝提取方法;朱力强等[10]也基于连通区域及Harris检测开发出一套裂缝图像匹配算法。不过上述研究仅以单一材料的表面裂纹为研究对象,而耐火材料种类繁多且形貌特征复杂,对相关的检测技术及方法有着更高的要求。随着机器学习和深度学习技术的不断发展,Adhikari等[11]基于神经网络和3-D可视化开发出混凝土裂纹量化和检测的集成模型;Wang等[12]提出将神经网络方法应用于路面裂缝检测,并使用主成分分析方法来计算并分析数据以提高计算机对裂缝的识别效率;Ouma等[13]借助小波变换及模糊C均值将路面裂纹缺陷和非缺陷的超像素聚类,并采用基于形态重构的精细分割进一步平滑和识别所检测到的破损轮廓。这些方法都是通过训练模型来识别所收集的图像数据特征,但仅专注于检测单一材料(混凝土或沥青)表面,并未涉及不同类型试样表面裂缝及大面积剥落的特征提取。有鉴于此,本文拟搭建视觉检测平台并采集样品初始图像样本,利用基于机器学习的方法对噪声、裂缝和剥落的连通域特征进行K-means聚类分析,通过设定误差系数E来计算其面积、周长、宽高比等连通域特征的分割阈值T,借助预处理和不同的连通域分割阈值来筛选识别试样裂缝和剥落等破损区域,引入链码计算破损区域的宽度和长度,并对骨架线进行区间划分来计算试样破损率,此外,还从图像处理和破损率计算两方面将本文所提方法与相关文献所报道的方法进行对比分析。
1 试验平台的建立及图像采集
1.1 试验平台的建立
本研究所建试验平台在国家标准[2]规定的抗热震性检测系统基础上增加了机器视觉模块,其结构见图1。该平台主要由相机、镜头、光源和电脑等硬件组成,耐火材料试样按相应国家标准要求制备。
1.2 图像采集
为保证试验结果的准确性,设定检测精度为0.1mm/pixels。根据文献[14]进行光学模块选型,工业相机为MER-502-79U3M型,镜头为M0804-MPW2型,光源为DH-WL50035型(波长450~460 nm)。在抗热震性检测过程中,共采集莫来石、黏土砖、氮化硅、陶瓷等4种不同材料试样的图像450张,因本研究对未出现破损特征的材料图像不做讨论,故先去除此类图像,再于剩余的390张图像中取310张用于聚类分析,80张用于最终的样品破损率计算,图2所示为检测开始之前4种试样受热端面的原始图像。

图1 基于机器视觉的耐火材料抗热震性检测系统

(a)莫来石 (b)黏土砖 (c)氮化硅 (d)陶瓷
2 图像处理
2.1 抗热震性试验及图像处理流程
利用增加了机器视觉模块的抗热震性检测系统对耐火材料试样开展高精度、全自动的抗热震性试验,主要检测流程见图3,其中视觉检测环节图像处理模块Ⅰ和模块Ⅱ的具体流程以及二者之间的关联如图4所示。
2.2 获取试样初始外边缘信息
随着抗热震性试验循环次数的增加,试样热端面会出现不同程度剥落,仅对该图像进行处理难以获取完整的边缘信息,故需先对试样初始图像进行边缘检测,获取试样掩模图像M1和外边缘轮廓M2,再对后续同组试验所得试样图像及掩模图像M1进行按位与操作以获取试样图像N1k(k为循环次数)。
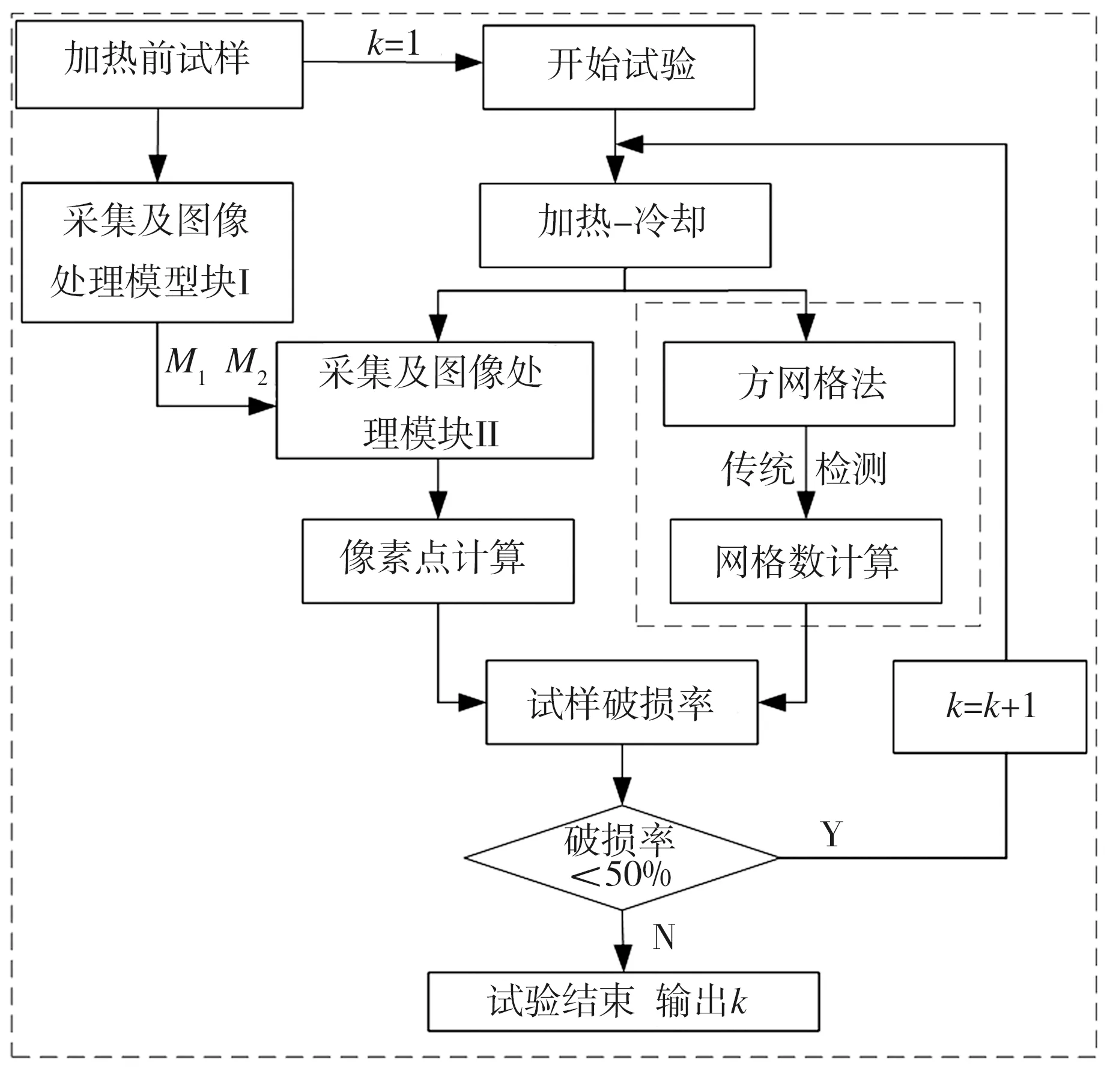
图3 抗热震性检测流程图
2.2.1 Laplacian变换
图5所示为莫来石材料在加热前的图像,借助Laplacian算子可检测出该图像在各方向上的灰阶突变,结果见图6。对于试样图像f(x,y),Laplacian算子定义如下:
∇2f=(∂2f)/(∂x2)+(∂2f)/(∂y2)
(1)
(∂2f)/(∂x2)=
f(x+1,y)+f(x-1,y)-2f(x,y)
(2)
(∂2f)/(∂y2)=
f(x,y+1)+f(x,y-1)-2f(x,y)
(3)
式中,▽2f为f(x,y)的二阶偏微分;(x,y)为图像像素点坐标。

图5 加热前的试样图像

图6 Laplacian变换结果
2.2.2 边缘信息提取
经 Laplacian变换后,图像中试样和背景对比度较大,灰度值差异明显,进一步采用基于阈值的分割方法对其进行外边缘检测。像素阈值运算所遵循的公式为:
(4)
式中,g(x,y)表示试样的二值图像,T1为阈值。
根据图6所示的像素点分布情况,将阈值T1设定为100来进行像素点分割,得到试样的二值图像,再将阈值化处理后的图像经形态学的闭运算[15]和轮廓索引,最终获得试样的掩模图像M1和外边缘轮廓M2,所得试样的二值图像、掩模图像及外边缘轮廓如图7所示。

(a)二值图像 (b)掩模图像M1 (c)外边缘轮廓M2
2.3 图像预处理及基于K-means聚类算法的连通域特征参数分析
以莫来石材料为例,首先采集其在抗热震性检测第7次循环时的图像并进行灰度化处理,再利用掩模图像M1与灰度图像进行按位与操作以获取去除周围背景干扰的试样图像N1k,由于图像N1k中背景与破损区域的灰度值分布区间存在交集,还需借助基于直方图均衡化[16]的方法将试样二值图像中的像素灰度值重新分配,从而获得图像N2k。又因试样表面特征复杂多样,受热端面图像有颗粒状或块状等噪声干扰,为了不影响后续的破损区域提取,还需对图像N2k进行形态学处理[16],一方面可有效滤除图像中小的麻点噪声干扰,减少图像中连通域的数量,另一方面可填充由噪声造成的裂缝间断,所得图像为N3k。上述图像预处理结果如图8所示,由图8(c)可知,试样图片经形态学滤波后,提取其中裂缝和剥落等破损区域时的干扰主要来自麻点和块状噪声,而裂缝、破损和噪声区域的形状特征差异较明显,所以可通过计算图像连通域的面积、周长以及宽高比等特征来去除噪声[9]。
在众多计算方法中,聚类分析算法是一种机器学习的重要算法[17],其中又以K-means聚类算法[18]相对较成熟,在医学影像处理、农田图像分析等领域均有一定程度的应用[19],该算法以欧氏距离作为相似性的评价指标,即认为2个对象的距离越近,其相似度就越高,算法具体工作过程为:1)随机选取K个点作为分类的中心点;2)按照距离最近原则,将每个数据点放到距离它最近的中心点所在的类中;3)重新计算各个分类的数据点平均值,将所得平均值作为新的分类中心点;4)重复步骤2和步骤3,直到分类稳定。经综合考虑,本研究采用K-means聚类算法对试样图像中噪声、裂缝和剥落的连通域特征进行分析,确定各连通域的面积(A)、周长(P)以及宽高比(R)特征分割阈值,相应的计算公式分别为:

(a)与运算结果 (b)直方图均衡化 (c)形态学滤波结果
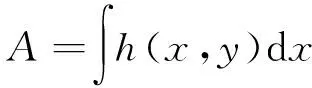
(5)
(6)
R=max{w/h,h/w}
(7)
式(5)~式(7)中,h(x,y)为连通域内中坐标 的像素点;Pe和Po分别为连通域边界轮廓线上链码为偶数和奇数的像素数;w、h分别为连通域最小外接矩形的宽和高。
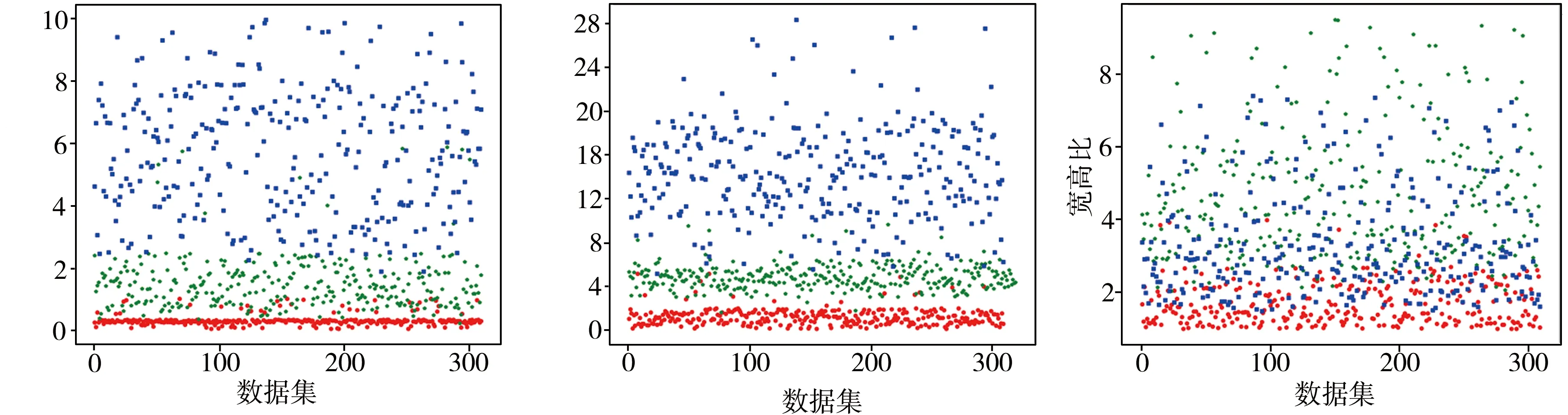
在进行聚类分析时,先将4种材料具有破损特征的图像共计310张经预处理后作为数据样本,再按破损特征在图像上划分出噪声、裂缝和剥落3种区域,即K值为3,对这3个区域的连通域面积、周长、宽高比分别进行聚类分析,相应的聚类中心点分析结果见图9,图中红色、绿色和蓝色分别表示噪声、裂缝和剥落。由图9(a)可见,对于图像连通域面积特征,剥落区域明显大于裂缝和噪声区域;由图9(b)可见,对于图像连通域周长特征,剥落区域也明显大于裂缝和噪声区域,与图像连通域面积特征具有相似的聚类分析结果;由图9(c)可知,对于图像连通域宽高比特征,裂缝区域较噪声和剥落区域更大。
(a)连通域面积 (b)连通域周长 (c)连通域宽高比
增大连通域特征参数的分割阈值T有助于筛除噪声,但T值过大也会筛除部分裂缝和剥落区域,而T过小则效果相反,故本文定义误差系数E用以评价分割效果,从而确定合适的分割阈值。设X、Y、Z分别为试样图像样本中噪声、裂缝和剥落连通域聚类中心点的矩阵,矩阵中元素总个数为N。以噪声和裂缝的面积连通域筛选为例,XA和YA分别表示噪声和裂缝连通域的面积特征聚类中心点的矩阵,将XA矩阵中每个元素均与面积分割阈值TA-XY进行比较,若大于TA-XY则该元素的值置为1,否则置为0,可得矩阵X′A;将YA矩阵中每个元素均与面积分割阈值TA-XY作比较,若小于TA-XY则该元素的值置为1,否则置为0,可得矩阵Y′A。噪声和裂缝连通域的面积特征误差系数EA-XY的计算公式为:
(8)

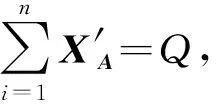
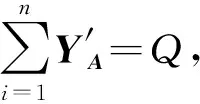

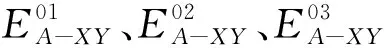
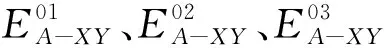
按上述步骤同理可以求得噪声和裂缝连通域的周长特征分割阈值TP-XY以及宽高比特征分割阈值TR-XY。不过,因剥落区域宽高比特征值一般小于裂缝特征值,利用计算所得TA-XY、TP-XY和TR-XY3个阈值对图像进行连通域筛除时,也会将部分剥落区域筛除,故还需按上述算法,同理计算出噪声和剥落的连通域面积、周长和宽高比等特征参数的分割阈值TA-XZ、TP-XZ以及TR-XZ。通过对310张样本数据图片进行聚类分析和计算,所得连通域特征参数分割阈值结果见表1。若样本数量增加,分割阈值也会动态调整。
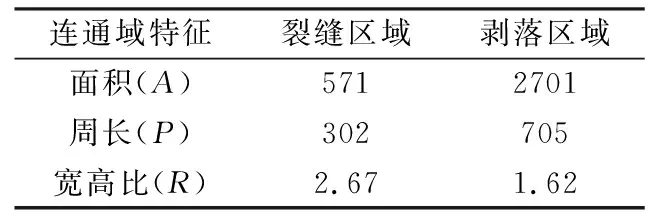
表1 分割阈值
为了验证基于K-means聚类的连通域特征参数分割方法的可行性,随机采集1幅试样图像(图10(a))并利用表1所列数据对该图像连通域特征进行分割处理,结果见图10(b),其中红色、绿色和蓝色分别表示噪声、裂缝和剥落。对比图10(a)和图10(b)可知,利用本文所提方法能够很好地划分出图像中的噪声、裂缝和剥落这3种区域。
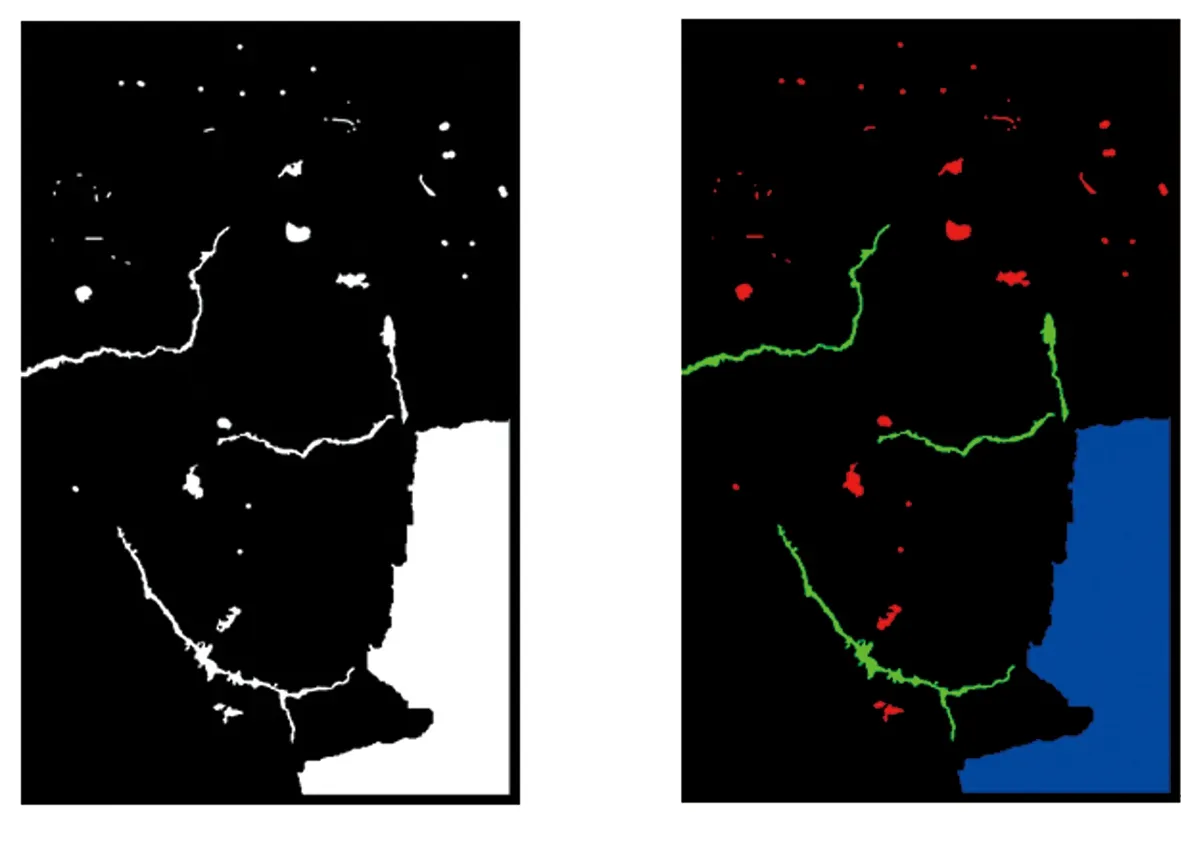
(a)示例图像 (b)分类结果
2.4 破损区域的提取
以莫来石材料为例,因试样图像剥落、裂缝等区域与四周边框相连,为了去除四周背景对后续连通域特征的影响,需将图像N3k(见图8(c))像素取反,再与试样外轮廓M2(见图7(c))进行图像按位或运算得到图像N4k(见图11),从而将试样与四周背景区域分隔开。

图11 或运算结果(N4k)
对同一图像,可分别通过裂缝和剥落两轮连通域特征值筛选来获取裂缝和剥落区域,再利用与运算得到完整破损区域图像,具体步骤如下:
Step1:由公式(5)计算图像N4k中所有连通域的面积Ai,若Ai小于面积分割阈值 ,则将该连通域中所有像素赋值为0,变成背景黑色,得到面积特征筛选后的图像N5k。
Step2:由公式(6)计算图像N5k中所有连通域的周长Pi,若Pi小于周长分割阈值 ,则将该连通域中所有像素赋值为0,变成背景黑色,得到周长特征筛选后的图像N6k。
Step3:由公式(7)计算图像N6k中所有连通域的宽高比Ri,若Ri小于宽高比分割阈值 ,则将该连通域中所有像素赋值为0,变成背景黑色,得到宽高比特征筛选后的图像N7k。
Step4:提取剥落区域,调整面积分割阈值、周长分割阈值、宽高比分割阈值分别为TA-XZ、TP-XZ和TR-XZ,对图像N4k重复步骤Step 1~Step 3,得到剥落区域图像N8k。
Step5:对图像N7k和N8k进行图像按位与运算,得到完整的破损区域。
按上述步骤并基于表1所列分割阈值数据对图像N4k进行相关运算,结果如图12~图13所示。由图12~图13可见,经3次连通域特征筛选后,试样图片中的麻点和块状噪声基本去除,处理效果理想。

(a)面积筛选N5k (b)周长筛选N6k (c)宽高比筛选N7k

(a)剥落区域提取结果(N8k)

(b)破损区域提取结果(N9k)
3 破损率计算
由国家标准[2]第5章可知,试样破损率计算需使用5 mm×5 mm的方格网(精度为1 mm)对相关区域进行测量,裂缝和剥落等破损区域的长度和宽度尺寸是衡量其是否属于破损率计算范畴的主要指标,因此检测出试样图像的裂缝和剥落区域后,还需定量计算其长度和宽度,具体流程见图14。
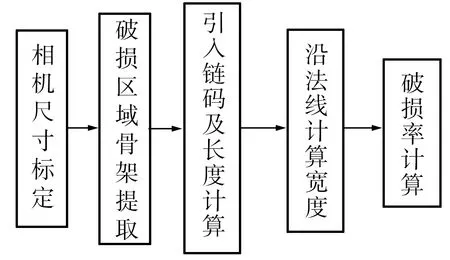
图14 破损率计算流程图
3.1 像素尺寸标定
本研究所获取的试样图像像素均为1352×2048,需做标定以计算像素尺寸和实际尺寸的比例。在测试开始前,先将一张40 mm×40 mm的白纸作为参照物置于试样之上并采图像如图15所示,测量出参照物的横向像素分布为305~1041 pixel,真实宽度为40 mm,则1像素标定值δ为:
δ=40/(1041-305)=0.054 mm/pixel
(9)
经多次标定求平均值,确定δ为0.055 mm/pixel,即1像素表示实际尺寸0.055 mm。

图15 像素尺寸标定
3.2 破损区域长度和宽度计算
测量试样破损区域长度时,可转化为计算破损中心线的长度,即对试样图像中裂缝和剥落区域进行骨架提取[20],仍以莫来石试样为例,获得相应的单层像素宽度的骨架图如图16所示。
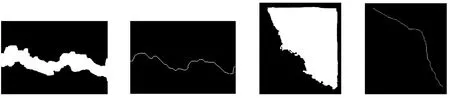
(a)裂缝区域图像 (b)裂缝骨架图 (c)剥落区域图像 (d)剥落骨架图
在破损骨架图像基础上引入Freeman链码来计算破损长度。常见的链码有4连通链码和8连通链码[20],本研究采用8连通链码。
对图像N9k(图13(b))进行轮廓查找,可获得莫来石试样图像中破损区域的连通域数量m,设某一破损区域为Cj(x,y),使用链码进行编码,计算链码的骨架长度作为破损的长度Lj,计算公式为:
(10)
式中:La、Lb分别表示破损区域边界轮廓线上链码为偶数和奇数的像素数。
在计算破损区域宽度时,可转换为计算骨架线上每个点法向像素点的个数,再参照文献[21]求得破损区域骨架上每个点(xi,yi)的宽度值Wi。
3.3 基于骨架线区间划分的破损率计算
在计算出莫来石试样图像每个破损区域Cj(x,y)骨架线的长度Lj以及骨架线上每个点的宽度值Wi之后,记某一破损区域Cj(x,y)骨架线上每个点宽度值Wi组成的区间为Dj,即Dj=(W1,W2…,WLj)。本研究以18 pixel(实际尺寸1 mm)为单位长度对Dj进行区间划分可得Lj/18个子区间,记为n,则任一子区间Dj-d=(W18d-17,W18d-16…,W18d)。将子区间内所有宽度值作为衡量其是否属于破损率计算范畴的指标,也就是说如果子区间Dj-d中每个宽度值Wi都大于或等于18,则该子区间的破损面积Sj-d为其宽度值累加和,否则该子区间破损面积记为0,即:
(11)
试样破损率G的计算公式为:
(12)
式中:S为莫来石试样掩模图像M1(见图7(b))中的白色像素点总个数。
通过上述图像处理及破损面积计算,最终可求得本文示例莫来石材料试样在抗热震性检测第7次循环时的破损率为12.47%。
4 算法实际应用效果分析
经2次连通域特征筛选及与运算后得到莫来石试样完整破损区域图像N9k,为定量评价其噪声和破损区域的分割效果,选用分割误差ER、假阳性率FPR和假阴性率FNR等评价指标[22]对分割后图像进行评价,这3个评价指标的值越低,表明图像处理效果越好。其中,分割误差ER是指实际分割面积与目标真实面积之间的误差值和目标真实面积的比率,假阳性率FPR为背景像素被误分割为目标像素的比率,假阴性率FNR为目标像素被误分割为背景像素的比率,三者的计算公式分别为:
(13)
(14)
(15)
利用本文所提算法、文献[8]所提自适应阈值法以及文献[10]所提基于特征点的匹配法等3种算法分别对后续抗热震性试验的50张破损图像进行处理。经3种算法计算所得误差均值见表2。从表2可见,利用本文基于K-means聚类和连通域特征筛选的图像识别方法所得评价指标ER、FPR和FNR的均值分别为3.73%、4.89%和1.82%,与利用自适应阈值法所得相应值相比,分别降低了1.14、1.83及0.33个百分点。与利用基于特征点的匹配法所得相应值相比,分别降低了1.39、1.78及0.02个百分点。由此可见,本文所提方法对裂缝和剥落等破损具有更好的识别效果。
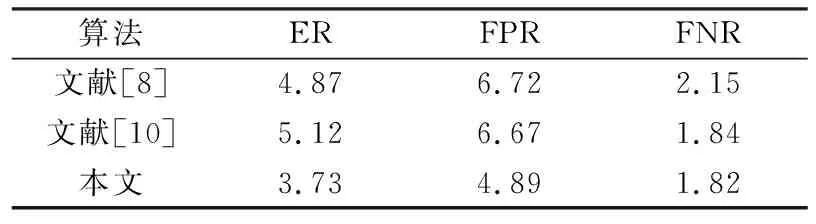
表2 误差结果对比(单位:%)
为评估本文所提出的破损率计算方法的计算效率及准确性,在后续进行抗热震性试验所得破损图像中选取4种材料的图像各20幅共计80幅,分别从检测时间和破损率相对误差两方面对比本文所提方法与传统方格网法[2],结果如表3所示。由表3可见,利用方格网法检测4种材料时,所用时间均值都超过了60 s,而利用本文所提方法检测时,相应耗时均值都在6 s以内,检测速度显著提高;对于破损率的计算,本文引入链码计算破损区域的长度和宽度并通过划分长度区间来计算局部破损面积,最终所得破损率计算结果与利用方格网法所得相应计算结果的相对误差均值都不超过3%。上述结果综合表明,本文所提检测方法检测速度快且检测结果精度高,完全满足实际抗热震性检测的要求。
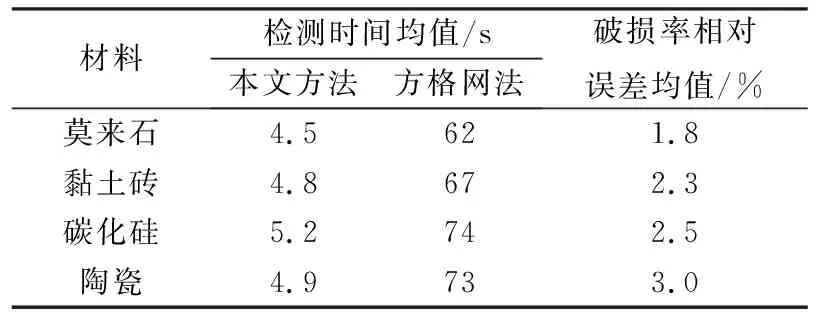
表3 破损率计算结果
5 结语
因传统的耐火材料抗热震性检测方法存在诸如效率低、安全性差、过程记录保存困难等不足,本文基于图像识别技术在标准抗热震性检测平台上增加了机器视觉模块对耐火材料试样开展了高精度、全自动的抗热震性检测研究。
针对待测耐火材料种类多样、检测过程中所采集的样品图像存在大量麻点、块状噪声、裂缝和剥落以及试样破损率计算时间较长等问题,借助机器学习方法对材料受热端面图像连通域特征进行聚类分析,提出了通过设定初始误差系数E来计算图像连通域面积、周长和宽高比特征分割阈值T的算法,对后续测试所采集的样品图像进行预处理及两次特征筛选来去除麻点和块状噪声,准确检测出裂缝和剥落区域。并且,若图像数据样本增加,其连通域特征参数分割阈值也会动态调整,提高了耐火材料的抗热震性检测智能化水平。此外,对材料破损区域进行骨架提取并引入链码计算其长度和宽度,提出基于骨架线区间划分的破损率计算方法,以子区间内所有宽度值作为衡量其是否属于破损区域的指标,将满足条件的子区域破损面积累加从而可准确计算出样品破损率。经取样检测,本文算法的分割误差、假阳性率和假阴性率平均值分别为3.73%、4.89%和1.82%,优于已有文献报道中利用自适应阈值法及特征点匹配法所得检测结果。

