城市路况下基于模型预测控制的汽车主动避撞策略

邹俊逸，吴伟伟，严运兵，龚 边

(1.武汉科技大学汽车与交通工程学院，湖北 武汉，430065；2. 深圳技术大学城市交通与物流学院，广东 深圳，518118)

追尾在车辆安全事故中占据了很大比重[1]，当车辆装备有前向碰撞预警和自动紧急制动系统时，追尾事故能够减少50%[2]。主动避撞系统作为智能汽车和无人驾驶技术的基础安全模块，是相关领域的研究热点。李霖等[3]根据紧急制动时驾驶员的行为构建危险估计模型，提出了两级预警和两级制动的避撞策略，根据危险估计模型计算出的危险等级选取相应的介入方式。刘贵如等[4]通过视觉和雷达传感器实时监测前方车辆，针对前方车辆行驶状态和不同类型车辆制动性能的差异，给出相应的安全距离估算模型和最小安全车距控制模型与算法。郑刚等[5]对驾驶员进行了分类，报警及制动阈值的修正则依据各类驾驶员的反应时间和驾驶速度之间的关系曲线，同时基于碰撞时间理论及模糊控制理论建立风险评估模型和制动减速度模糊控制模型。郑苏等[6]采用VTH(variable time headway)算法建立汽车的纵向行驶模型，提出了一种基于车辆纵向分层控制结构的三级制动控制避撞策略。胡朝辉等[7]通过估算当前行驶路面的附着系数来估算最大制动减速度，从而调整制动强度，并根据安全距离模型设计出主动避障算法。当采取横向避撞所需的纵向距离小于直接纵向避撞所需纵向距离时，若错过最后的制动机会则可通过转向实现避障[8]。上述研究主要侧重纵向制动以避免碰撞，对横向转向避撞轨迹描述不够准确，无法确保汽车紧急制动时的横向安全性。

模型预测控制(model predictive control, MPC)能根据车辆当前的运动状态预测其未来轨迹，实现对目标函数的在线滚动优化[9-10]。MPC是一种最优化控制，包括预测模型、滚动优化和反馈校正三个核心部分，本文针对城市路况下的车辆主动避撞问题，基于模型预测控制器采用分层控制策略，上层模块根据车辆运动学理论采用Sigmoid函数对局部避撞路径进行规划，下层模块根据车辆动力学理论控制前轮转角，对避障轨迹进行跟踪控制，从而实现车辆主动转向避撞。

1 车辆制动过程及其动力学模型

1.1 车辆制动过程

本文研究场景如下：

(1)车辆在城市道路上行驶，道路设计规范，避撞环境良好；

(2)车辆行驶速度在80 km/h以下；

(3)车辆极限制动避撞距离小于安全距离，极限转弯避撞距离大于安全距离。

汽车采用电子控制，忽略驾驶员反应时间。触发制动时，制动踏板力、汽车制动减速度与制动时间的关系曲线如图1所示，图中Fp为踏板力，ab为纵向加速度最大值，τ1为克服制动器内部间隙所需时间，τ2为制动器制动力增长阶段历时，制动器作用时间一般在0.2～0.9 s[11]。

从开始操纵制动控制装置到汽车停止所驶过的制动距离为：

(1)

式中：ua0为初始制动车速。

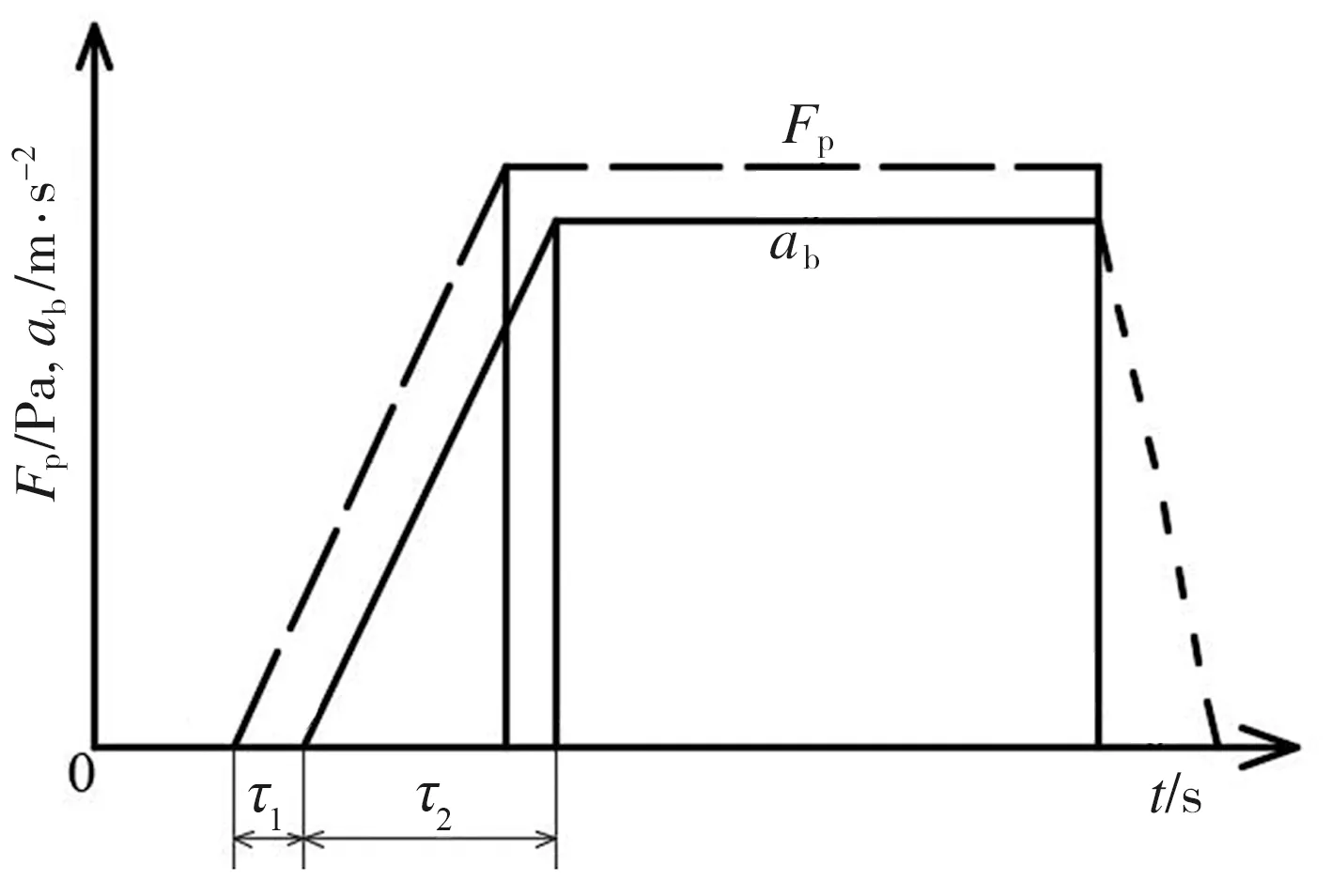
图1 制动关系曲线

1.2 车辆动力学模型

Liu等[12]基于MPC对危险规避算法保真度进行研究，结果表明，低自由度模型添加满足行驶工况的约束条件，可以在很大程度上减少计算时间，并且能够达到高自由度模型的应用效果。对于城市路况下紧急转向避撞的危险场景，为提高模型预测控制器的实时性和稳定性，本文建立三自由度动力学模型，研究车辆制动和转向控制过程。

为提高控制器的准确性，做如下假设：①不考虑车辆垂向运动；②忽略悬架对车辆动力学的影响；③不考虑载荷对车辆动力学的影响；④忽略空气动力学因素影响。具体模型如图2以及式(2)～式(4)所示。

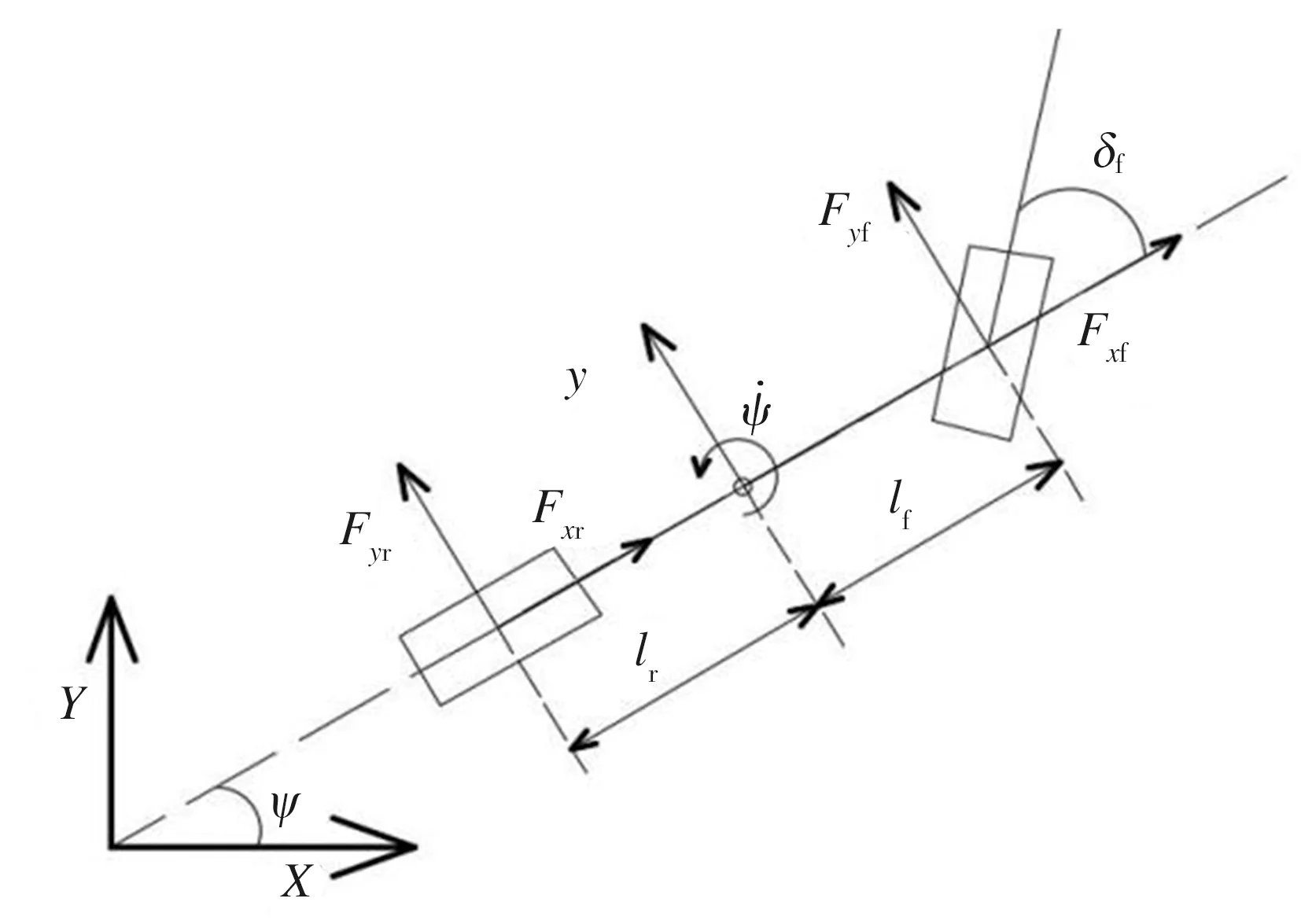
图2 车辆动力学模型

(2)

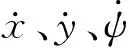
当车辆的前轮转角和横摆角很小时，轮胎侧向力和侧偏角有如下线性关系：

(3)

(4)

式中：αf、αr分别为车辆前、后轮侧偏角；Ccf、Ccr分别为车辆前、后轮侧偏刚度；δf为前轮转角。

为便于避障轨迹的规划，将车辆质心坐标转换到惯性坐标系中：

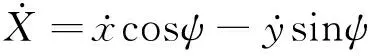
(5)

(6)

2 避撞路径规划和避撞控制策略

2.1 避撞轨迹

采用Sigmoid函数可以规划出转弯起点与终点间的轨迹，其具有实时性好、算法简洁的优点，能够结合物理避撞约束实现对汽车避撞路径的实时规划。

Sigmoid函数表达式为：

(7)

k=wze-ac

(8)

式中：a、c、λ、wz为参数。a决定了曲线的斜率；c为斜率最大时车辆所处的纵向位置;wz决定了避撞路径横向位移；λ决定了规划轨迹的横向起点。

基于Sigmoid函数的避撞轨迹以及参数c和wz对轨迹的影响如图3所示。

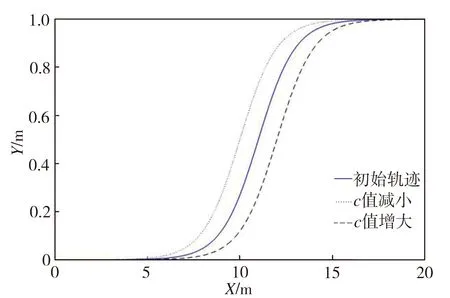
(a) c对轨迹的纵向影响

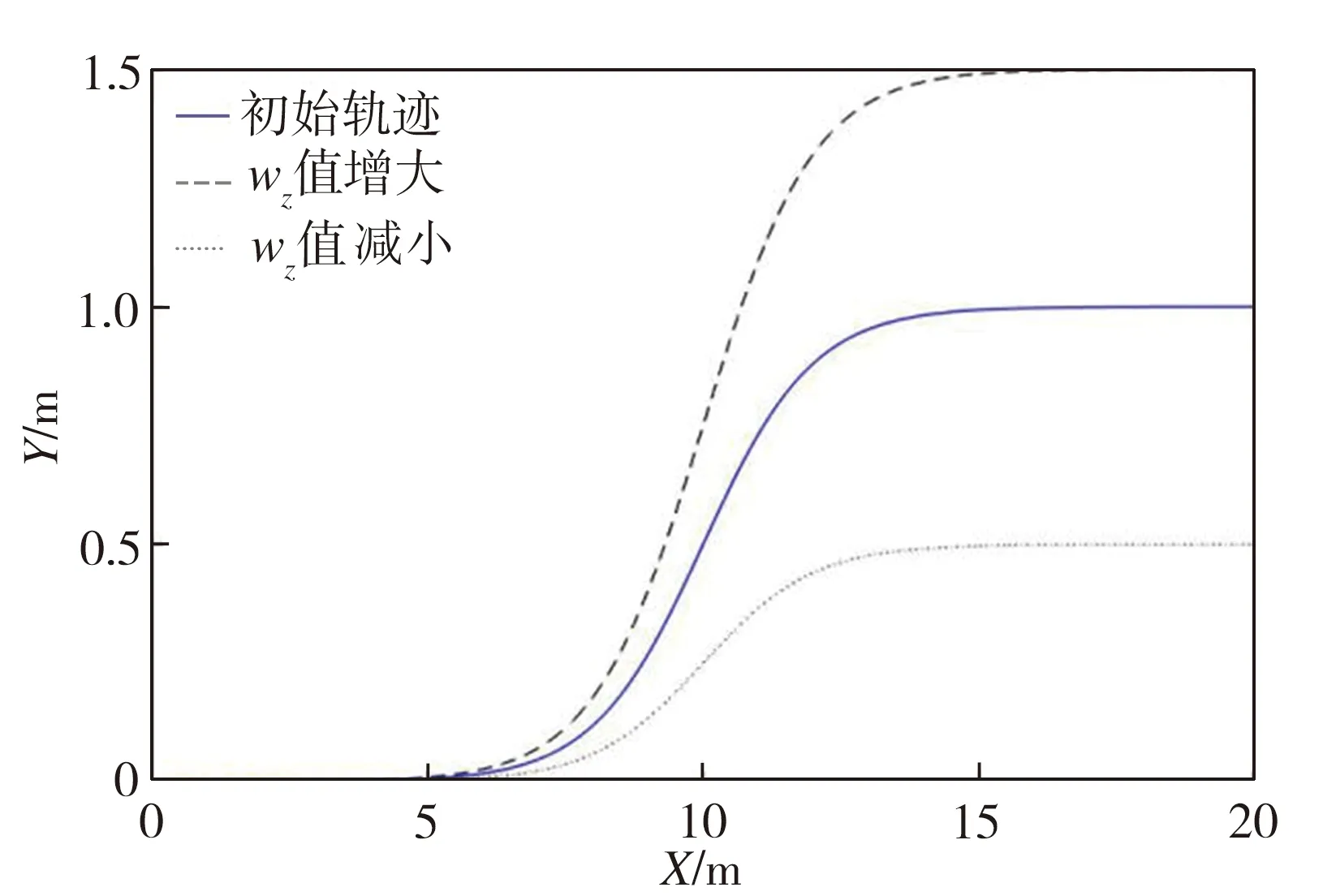
(b) wz对轨迹的横向影响

2.2 主动转向避撞策略

为保证车辆紧急转向避撞的稳定性，转向与制动不在同一时刻执行。裴晓飞等[13]通过比较转向与制动的优先级发现，在高附着系数路面上，转向优先级随着车速下降而提高；在低附着系数路面上，转向优先级随着车速上升而提高。

本文采用的安全距离模型如图4所示,转向避撞位置关系如图5所示。为了便于研究，在干燥路面(附着系数μ取0.85)上的转向避撞控制中，控制制动优先级高于转向优先级；在冰雪路面(μ取0.2)上的转向避撞控制中，控制转向的优先级高于制动优先级。

图4 安全距离模型示意图

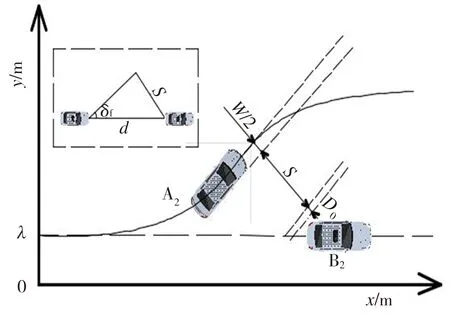
图5 转向避撞位置关系图

图4中，A1、A2为自车纵向位置，B1、B2为前车纵向位置，由自车和前车的运动关系得到：

d0=d1-d2+D0

(9)

式中：d1为自车纵向运动距离；d2为前车纵向运动距离；d0为自车与前车保持的安全车距；D0为车辆的车身安全范围。

基于式(7)中参数k，由自车宽度W、避撞安全距离和前车车身安全距离可以确定避撞路径规划时所需的横向位移Sw(式(10))，根据制动性能(式(1))可以确定汽车制动时所需的纵向位移。

Sw=W/2+dsinδf+D0

(10)

在避撞环境中，车辆通过毫米波雷达检测障碍物信息，当规划层接受到障碍物信息后，采用Sigmoid函数规划出新的避撞轨迹。基于MPC控制，如图6所示建立分层控制策略，MPC控制器通过求解满足各种约束条件的优化问题，将当前时刻的最优控制序列u*(t)输出到被控平台，经状态估计器将估计状态量x(t)输入到控制器再次优化求得下一时刻解。图6中Xre(t)、Yre(t)表示期望坐标点，δf,re(t)表示期望转角。

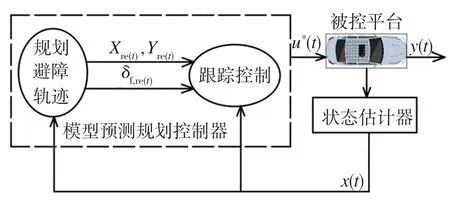
图6 主动避撞控制器

上层轨迹规划层的核心是在满足约束的前提下缩减车辆与参考路径的偏差。参照文献[14]采用带有权重因子的代价函数进行线性组合，见式(11)～式(13)，选择安全性和平顺性代价最小的路径为期望路径。

J[i]=ϖaCa[i]+ϖpCp[i]

(11)

式中:Ca、Cp分别为安全性与平顺性代价；ϖa、ϖp为权重因子；i为检索路径序号。

(12)

式中：M[·]为碰撞检测值，通过障碍时取0，未通过障碍时取1；g[·]为判断障碍物影响范围的因子；N为障碍物影响范围的边界值。

(13)

式中：κi(s)为路径曲率。

不同权重因子对路径选择的影响程度不同。在检索出不同路径后，综合安全性和平顺性,选择碰撞风险较低和平滑性较好的路径。

利用下层控制器进行轨迹跟踪时，结合线性轮胎模型式(3)～式(4)可得动力学非线性模型如下：

(14)

式中：sr为后轮滑移率；Clf为Clr分别为前轮和后轮的纵向刚度。

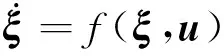
(15)

对当前时刻的控制量和状态量进行泰勒展开，忽略高阶项，有

(16)

由式(16)与式(15)作差得：

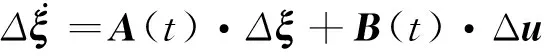
(17)

其中，

采用一阶差商代替微分对式(17)进行离散化处理，得到系统离散化的线性预测模型如下，其中A(k)、B(k)由欧拉一阶差分离散化获得。

ξ(k+1)=A(k)ξ(k)+B(k)u(k)

(18)

(19)

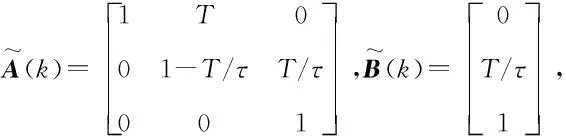
令Np为预测时域、Nc为控制时域，可得预测范围内预测输出与当前时刻状态的预测方程为

Y=ψkr(k|t)+ΘkΔU(k)

(20)

其中，

由式(15)可知，在预测时域内的输出量和状态量能够通过系统当前的状态量ξ(k)和控制时域内的控制增量ΔU得到。

为保证车辆转向不超过物理限制，同时满足转向避撞的稳定性，对前轮转角设置约束条件如下：

-20°≤δf≤20°

(21)

转向时，车身朝向和车辆航向不一致将导致质心侧偏角增大，车辆的横向稳定性可用质心侧偏角作部分表征[15]。为防止车辆出现侧翻现象，对质心侧偏角β设置约束如下：

(22)

3 仿真实验与结果分析

3.1 联合仿真实验

为验证本文方法对车辆避撞控制的可行性，在PreScan汽车驾驶仿真软件中建立避撞场景如图7所示。基于CarSim和Matlab/Simulink建立联合仿真模型，设计路面附着系数μ为0.85和0.2，分别对应城市干燥路面和冰雪路面。在高附着系数路面上分别设置20、60、80 km/h三种车速工况，考虑到国家交通安全法的规定，在冰雪路面上车速不能高于30 km/h[16]，所以在低附着系数路面上分别设置10、20、30 km/h三种车速工况。设置车辆为前轮驱动，车辆主要参数如表1所示。

(a)避撞控制中

(b)避撞控制后

表1 车辆主要参数

3.2 仿真结果分析

3.2.1 路径规划与轨迹跟踪效果

图8为城市干燥路面上不同车速时自车遇到障碍物的路径规划和轨迹跟踪结果。从图8可以看出，当车速从20 km/h升到60 km/h时，控制器对路径规划的起始距离提前了5 m，同时横向位移增加了0.25 m，保证了横向安全距离，这表明车辆在高速和低速行驶过程中均能提前规划出安全避撞轨迹。最大斜率处的最小纵向剩余距离为2.6 m，保证了避撞安全性，控制器根据评价函数选取了最优路径。

下层控制器中的期望轨迹为上层控制器选择的最优路径，为验证轨迹跟踪性能，选取固定轨迹和路面,分别以20、60、80 km/h车速进行跟踪对比。由图8(d)可以看出，车辆在不同车速工况下均可实现对规划轨迹的自主跟踪。

3.2.2 避撞性能分析

为了进一步验证控制器的避撞控制性能，下面分析不同速度的车辆在两种路面上避撞时的动力学特性。图9和图10分别为控制器对高附路面和低附路面上车辆的控制效果。由图9(a)可以看出，在高附路面上，速度为60 km/h和80 km/h的车辆进行避撞时，控制器对前轮转角的控制时间比车速为20 km/h时分别提前了2.75 s和3.55 s。由图10(a)可以看出，在低附路面上，速度为20 km/h和30 km/h的车辆进行避撞时，控制器对前轮转角的控制时间比车速为10 km/h时分别提前了2.62 s和4.35 s。上述结果表明，当车速提高时，控制器能够对车辆提前进行转向避撞控制。另外，在两种路面的不同车速下，前轮转角均在±20°的限制范围内，表明该控制器对前轮转角的控制具有较好的鲁棒性。

(a)20 km/h车速路径规划

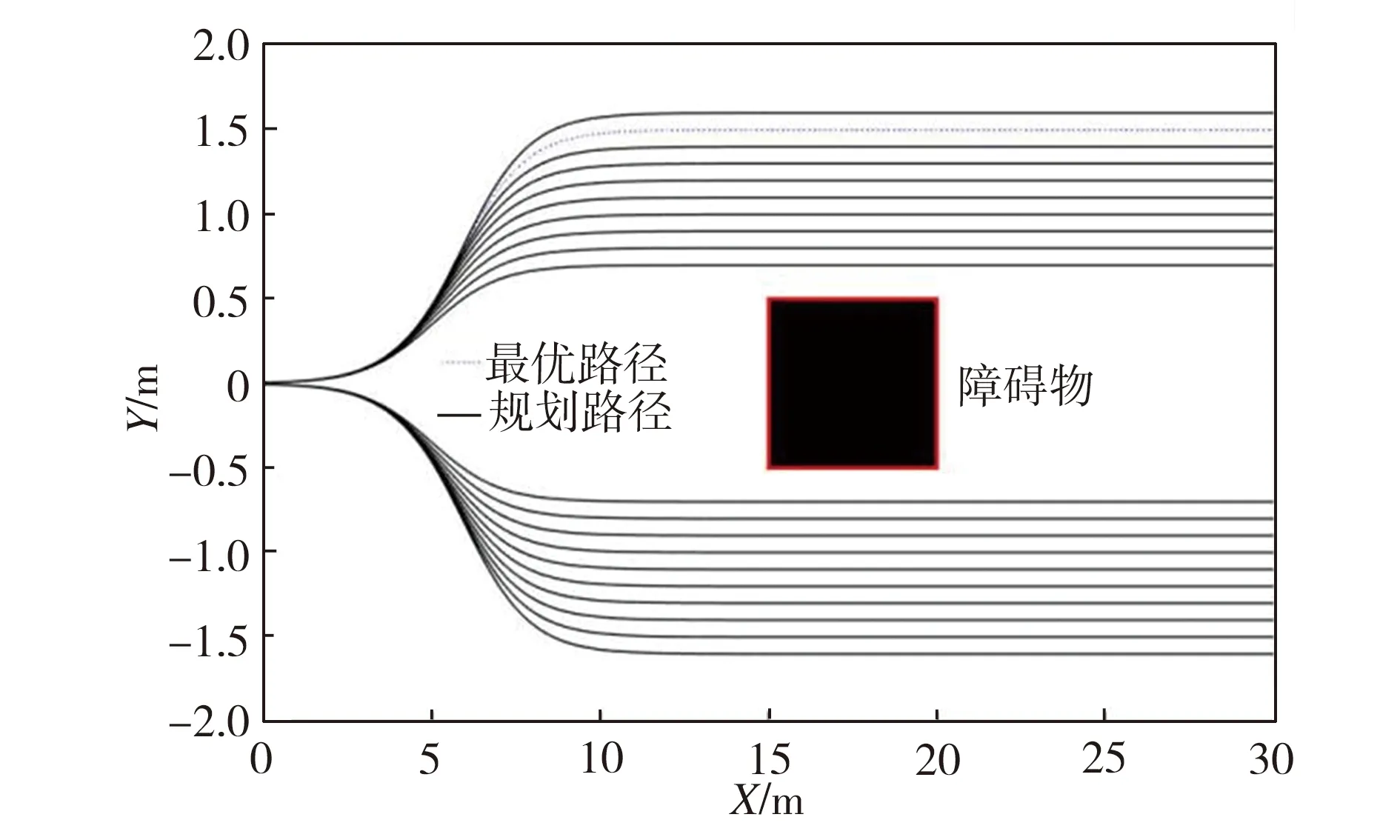
(b)60 km/h车速路径规划

(c)80 km/h车速路径规划

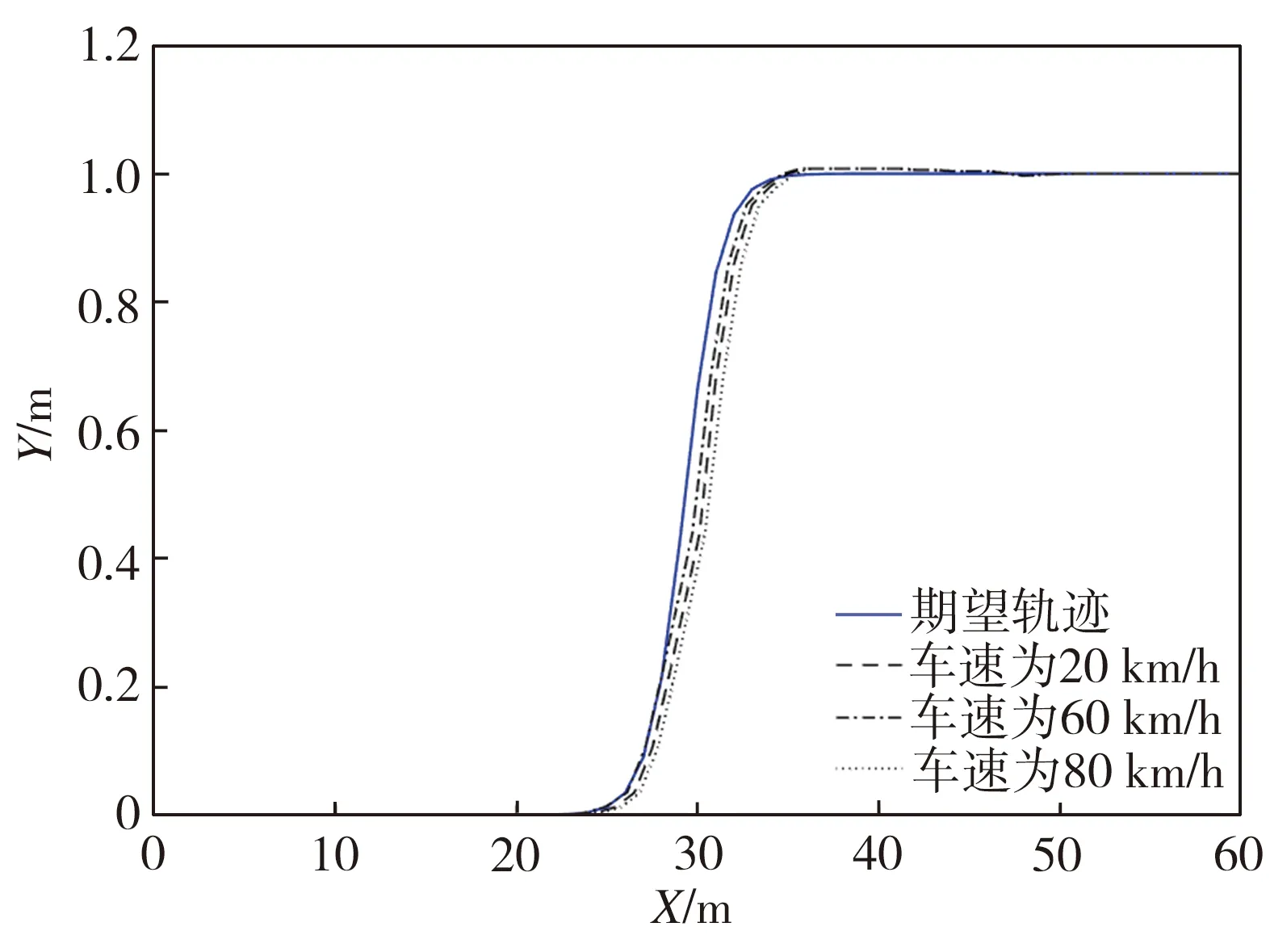
(d)轨迹跟踪结果

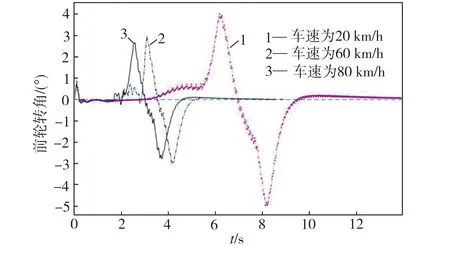
(a) 左前轮转角对比

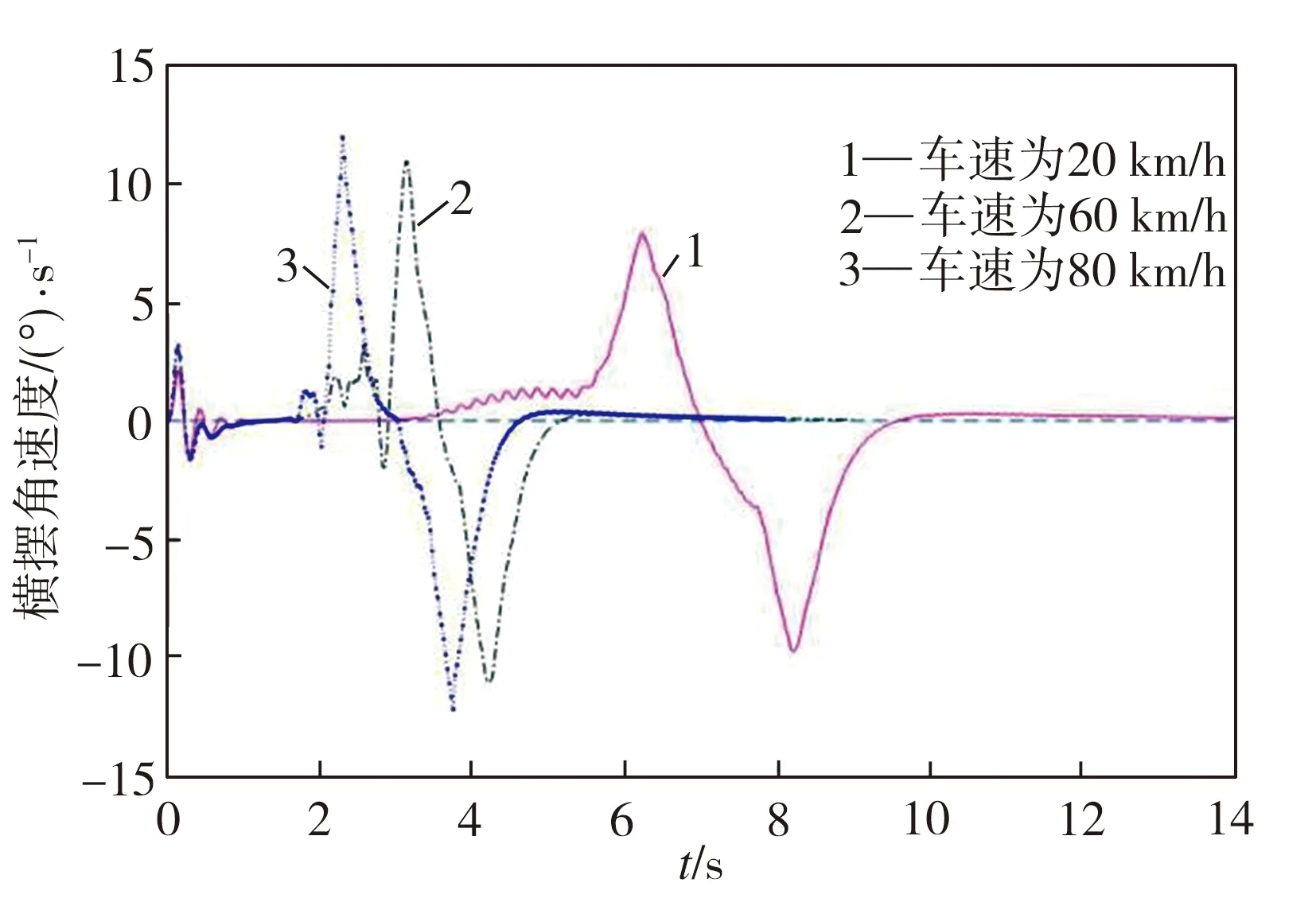
(b) 横摆角速度对比

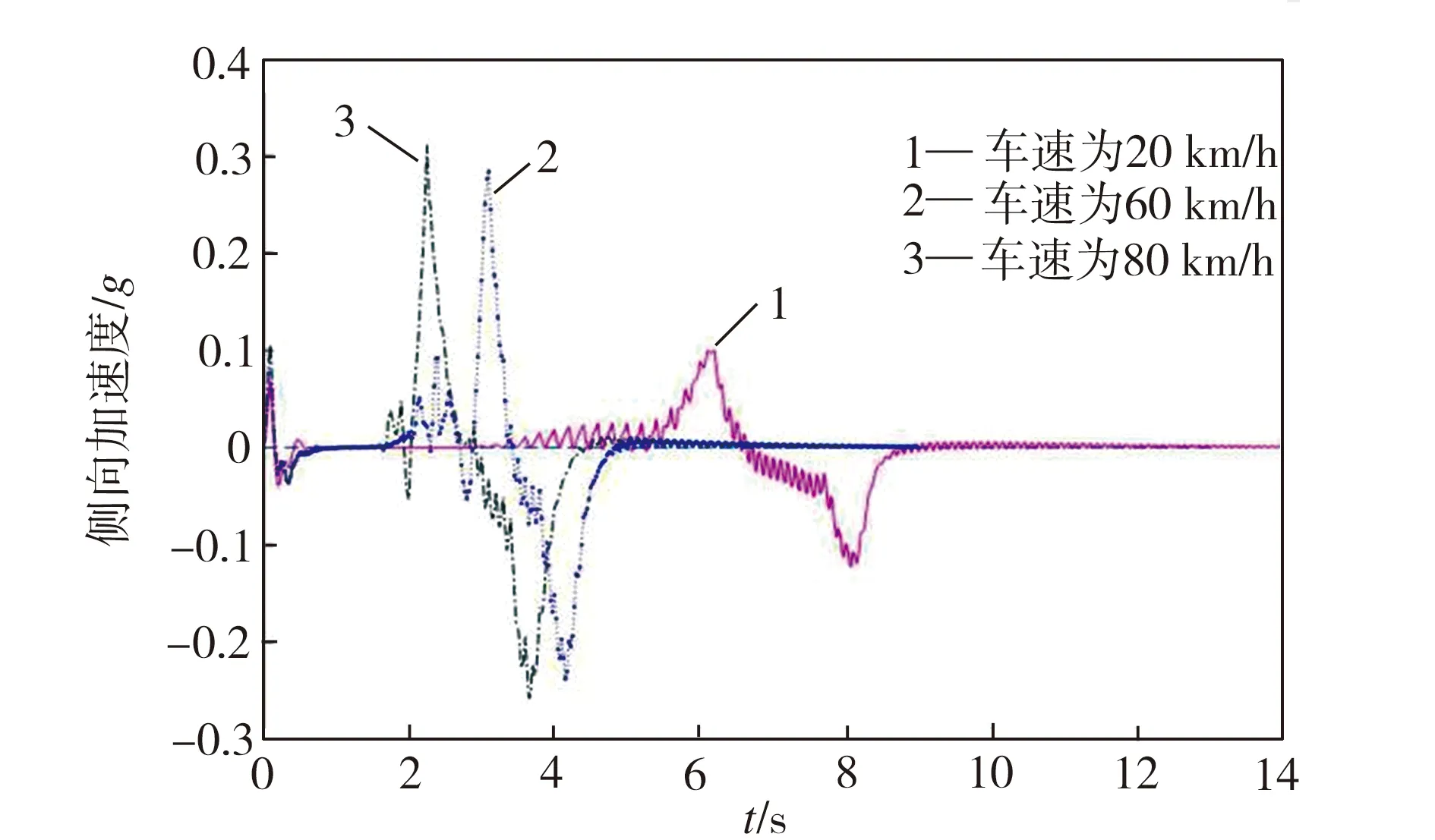
(c) 侧向加速度对比

如图9(b)和图10(b)所示，随着车速的增加，转向避撞时车辆横摆角速度有所提高。在高附路面上，三种车速的车辆转向避撞时，横摆角速度峰值不超过12.18°/s；在低附路面上，三种车速的车辆转向避撞时，横摆角速度不超过9.21°/s；以上结果均在15°/s的行业经验限制范围[17]内。

(a) 左前轮转角对比

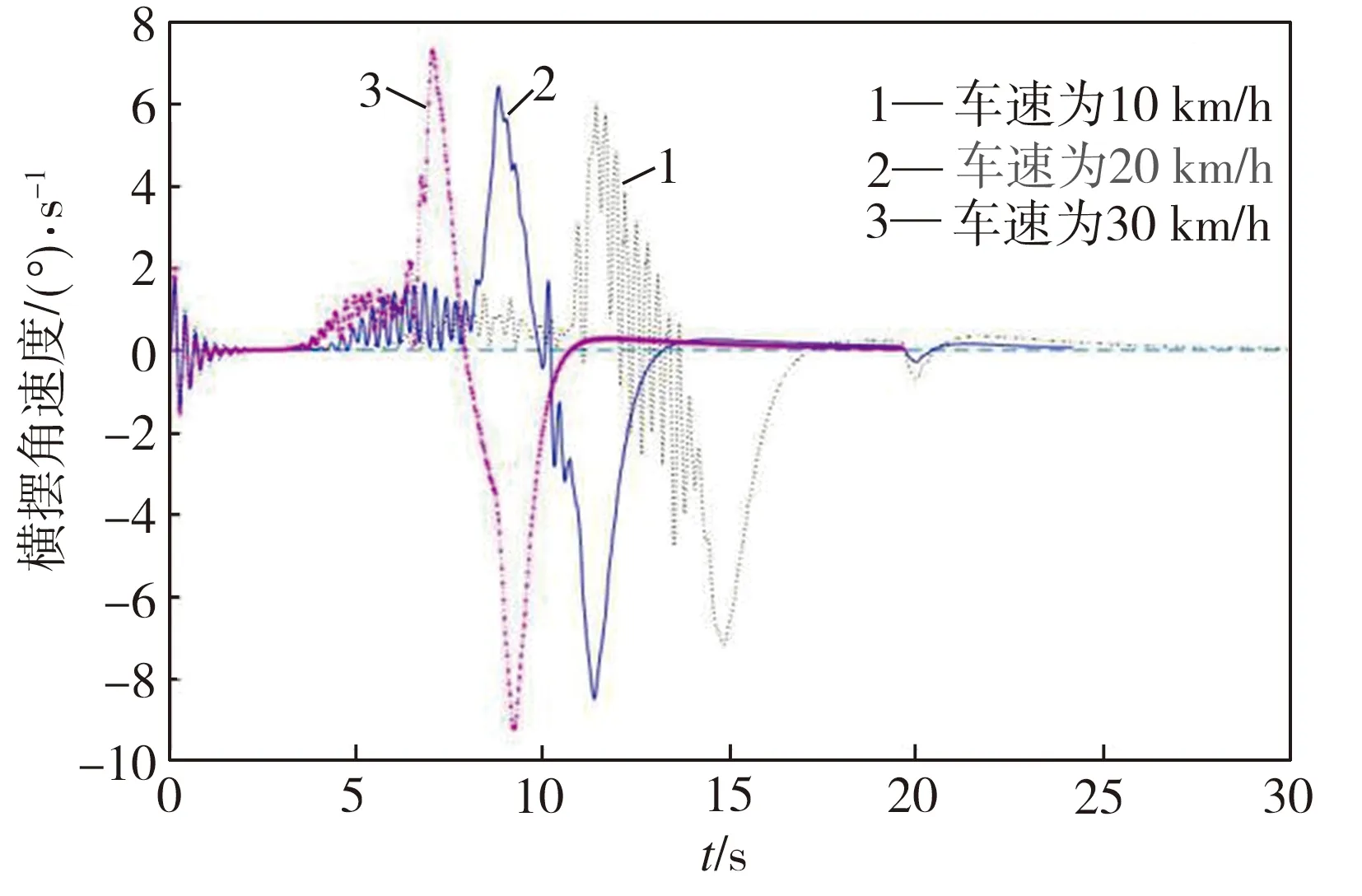
(b) 横摆角速度对比

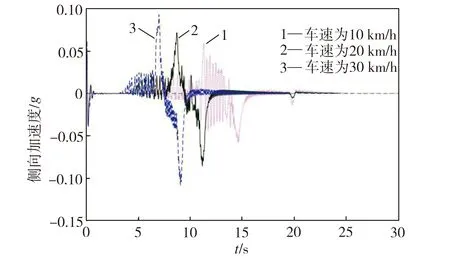
(c) 侧向加速度对比

结合图9(c)和图10(c)可以看出，在两种路面上，不同车速工况下车辆的侧向加速度绝对值均没有超过0.4g的行业经验限制[17],车辆处于稳定状态，保证了轨迹跟踪的稳定性。

4 结语

本文针对城市道路智能汽车紧急避撞问题，提出了主动转向避撞策略，设计了基于MPC并采用路径规划和跟踪避撞分层控制架构的控制器，还搭建了联合仿真平台对所提方法进行验证。仿真实验结果显示，该控制器能够很好地实现车辆在不同车速和路面工况下对避撞路径的主动规划和有效跟踪，具有较好的稳定性和实时性，使得在无法通过单一制动避免碰撞的情况下，仍可利用转向避撞方式避开障碍物。