六轴机械臂神经网络自适应终端滑模控制

贾华,刘延俊,4,王雨,薛钢

(1.山东大学机械工程学院,250061,济南;2.山东大学高效洁净机械制造教育部重点实验室,250061,济南;3.山东大学机械工程国家级实验教学示范中心,250061,济南;4.山东大学海洋研究院,266237,山东青岛)

作为一种高性能自动化设备,机械臂能够提高生产效率和质量,得到了越来越广泛的应用。机械臂是一个高度非线性、强耦合、多变量的时变系统,因此需要高性能的控制器对其进行可靠控制。

机械臂在执行任务时,通常需要跟踪特定的轨迹,并保证一定的精度。常见的传统PID控制器在受到外部干扰影响时,其动态特性和鲁棒性并不理想。为解决这一问题,国内外学者提出了多种类型的机械臂控制算法,例如神经网络控制[1-2]、模糊控制[3]、滑模控制[4-5]、鲁棒控制[6]、迭代学习控制[7]、反步控制[8-9]等。其中滑模控制物理实现较为简单,且对扰动不灵敏,在机器人领域得到了广泛应用。敖天翔等[10]将滑模控制器应用于双臂机器人,得到了较好的定点控制和轨迹跟踪控制效果,但是忽略了实际机械臂中存在的摩擦力。Baek等[11]结合极点配置和时延估计方法设计了一种自适应滑模控制器,通过反馈补偿能够获得理想的闭环极点,但是没有考虑外界干扰的影响。

随着变结构控制理论的发展,出现了性能更好的终端滑模控制。与传统滑模相比,终端滑模控制能够保证系统在有限时间收敛[12]。吴爱国等[13]提出了一种非奇异快速终端滑模控制(NFTSMC)方法,在切换控制中引入连续终端吸引子,保证了系统在有限时间内稳定,并利用Lyapunov方法进行了证明。Yang等[14]研究了非线性系统的终端滑模控制,将非奇异快速终端滑模控制应用在了二关节机械臂控制上,具有比传统滑模更好的控制性能。Zhang等[15]针对动力学参数部分不确定的机械臂系统,提出了一种全局近似终端滑模控制方法,避免了奇异问题,保证了系统在有限时间收敛。

在实际环境下,由于存在着摩擦、外界干扰、模型误差等不确定性因素,采用滑模控制时需要对这些变量进行保守估计,切换增益会随之增大,容易引起较大的抖振,影响控制效果。针对这一问题,董君等[16]在非线性积分滑模的基础上,引入RBF神经网络(RBFNN)来估计动力学参数,减小了抖振。Guo等[17]将滑模和增量PID结合起来,提出一种RDRBF控制算法,利用神经网络补偿模型不确定项,保证控制力矩平滑,在串联机械臂上得到了较好的控制效果。

目前,多数文献提出的控制算法只在平面二连杆机械臂上进行了验证。本文在上述研究的基础上,针对模型不确定且存在外界干扰时的六轴机械臂系统,提出了一种基于动力学模型分块逼近的神经网络自适应终端滑模控制算法(RBFTSM)。首先,利用多个RBF神经网络分别逼近动力学模型中的系数矩阵,并结合非奇异终端滑模超曲面设计控制律,依靠自适应律对权值的在线调整,实现对机械臂动力学模型的重构,整个过程无需复杂的动力学建模计算;然后,设计了一种积分滑模控制鲁棒项,对模型重构误差和外界干扰进行消除,采用Lyapunov稳定性定理证明了系统能够在有限时间到达稳定;最后,在Simulink环境下对六轴机械臂进行仿真分析,与PID算法和文献[18]中提到的RBF神经网络整体逼近滑模控制算法相比较,验证该控制方法的有效性,为六轴机械臂的轨迹跟踪提供一种可行的控制方案。

1 模型描述

本文以UR机械臂为研究模型,其坐标系的建立采用改进Denavit Hartenberg(MDH)法,如图1所示。

根据拉格朗日法[19],机械臂的动力学模型最终可写成

(1)

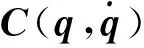
性质1[20]惯性矩阵M(q)是对称正定矩阵,存在正数m1、m2,满足如下不等式

m1‖x‖2≤xTM(q)x≤m2‖x‖2

(2)

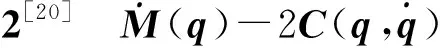
(3)

引理1[21]全局有限时间稳定的Lyapunov函数定理。

(4)

那么系统为有限时间稳定,而且系统的收敛时间T(x)满足

(5)

引理2[22]范数不等式‖x‖2≤‖x‖1,对于一个向量x=[x1x2…xn],总是满足

(6)

没有特别说明的情况下,本文的‖·‖表示2范数。

引理3[22]Cauchy-Schwarz不等式,对于向量空间V中的任意向量u和v,有

|〈u,v〉|≤‖u‖·‖v‖

(7)

2 控制器设计

2.1 终端滑模面(TSM)设计

设机械臂关节目标角度为qd(t),实际角度为q(t),定义跟踪误差为

e(t)=qd(t)-q(t)

(8)

(9)

在传统滑模控制中,滑模面的选取一般为线性滑模面,即

(10)

当系统状态到达滑模面时,线性滑模面能使误差渐进收敛到0,但是不能保证在有限时间内收敛。终端滑模面则能够确保误差变量在有限时间内收敛到0[23]。

本文取非奇异终端滑模面[24]

(11)

式中:α,β>0,p、q均为正奇数,且p>q。

对式(11)进行求导可得

(12)

(13)

式(13)两边同时乘以M(q),可以得到

(14)

(15)

(16)

根据式(15)、(16)可以将式(13)重新修改为

(17)

理想状态下,机械臂模型参数均精确已知,此时可以取控制律为

τ=τm+τu

(18)

其中

τu=K1sgn(r)

取Lyapunov函数

(19)

对其求时间的导数

(20)

根据式(17)、(18)可以将式(20)进一步写成

-(λmin(K1)-‖τd‖)‖r‖

(21)

其中K1∈n×n为正定对角矩阵,λmin(K1)是矩阵K1的最小特征值,只要选择合适的K1使其大于外界干扰τd的上界,就可以保证根据Lyapunov稳定性判定,系统是稳定的。在实际情况下,机械臂的模型参数不可能是精确已知的,因此需要对控制律式(18)做进一步修改。

2.2 RBF神经网络分块逼近

在实际应用时,机械臂的动力学模型很难精确获得,存在较大的建模误差,影响控制器的性能。为了解决这一问题,本文采用RBF神经网络来实现对机械臂模型参数的估计。

RBF神经网络由输入层、隐含层、输出层组成。其结构如图2所示[16]。

RBF神经网络中的径向基函数采用高斯基函数,表达式如下

(22)

(23)

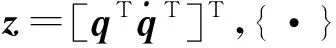
神经网络逼近结果可以表示为

(24)

可以将式(17)表示为

(25)

其中

(26)

式中:E表示神经网络逼近误差,表达式为

(27)

假设1不确定项E+τd有一个上界,表示为

‖E+τd‖≤ρ

(28)

其中ρ是一个已知的正数。

(29)

则总的逼近误差可表示为

(30)

(31)

对控制律式(18)进行进一步修改,引入RBF神经网络模型补偿项

(32)

(33)

总的控制律可以表示为

(34)

式中:Kp,Ki,Kr∈n×n,均为正定对角矩阵;τm代表了RBF神经网络逼近的模型补偿项;τu中的Kpr为滑模控制项,保证系统到达稳定;Krsgn(r)用于抑制外部干扰和模型重构误差,提高抗干扰能力;项是用于进一步消除神经网络的逼近误差和外界干扰的影响。

设计神经网络权值自适应律为

(35)

式中:ΓMk>0;ΓCk>0;ΓGk>0;ΓFk>0;参数k的取值为k=1,2,…,n。

2.3 控制系统稳定性分析

定义Lyapunov函数为

(36)

对Lyapunov函数求导可得

(37)

(38)

根据引理2、3以及假设1,有

(39)

式中:λmin(Kr)表示Kr矩阵的最小特征值,可以通过选取较大的Kr使得λmin(Kr)大于不确定上界ρ,则

(40)

有限时间稳定证明如下:取Lyapunov函数

(41)

对式(41)进行求导得

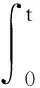
(42)

因为高斯基函数值域为区间[0,1],也就表明激活函数都是有界的,根据前面的有界分析结论,可以得到

(43)

其中η是一个正定对角矩阵,η∈n×n,代入式(42)中得

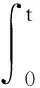
rT(τd+E)-rTKpr-rTKrsgn(r)

(44)

选择Kp≥η,并根据引理2、3可推得

(45)

由于控制律τ中引入了符号函数sgn,因此可能会导致系统发生抖振,影响控制效果。传统滑模控制中消除抖振的方法主要是边界层法,但是不能保证系统是有限时间收敛的,为避免该问题,本文取如下函数[26]

(46)

式中Δ是一个正数,表示边界层的厚度。

此时控制律转换为

(47)

当|r|≥|Δ|时,有限时间稳定证明同前,当|r|<|Δ|时,取Lyapunov函数

(48)

(49)

事实上,总会存在一个很小的数满足μ≤(|r|/(|r|+Δ)),有

(50)

根据引理1,有限时间收敛得证。

本文提出的控制系统的原理如图3所示。其中分项逼近的M、C、G、F中的每一个元素都是一组神经网络,因此该控制器易于实现并行处理,适合实时实现。

3 仿真分析

为验证本文提出的机械臂控制算法的有效性和可靠性,利用Simulink中的Simscape工具箱搭建六轴机械臂的物理模型,进行仿真实验,仿真模型如图4所示。

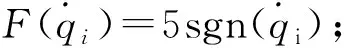
将本文算法的仿真结果与传统PID控制和文献[18]中提到的RBF神经网络整体逼近滑模控制算法进行对比分析。以关节1、2、3为例,得到的仿真结果如图5～10所示。

分析图5～图9可得,3种算法均能在一定误差范围内跟踪特定轨迹,而且由于关节2和关节3靠近底座部分,关节负载变化比较大,轨迹跟踪的效果对比就比较明显。通过对比其误差曲线图6可知,本文提出的算法具有更好的稳态特性,更小的误差

波动范围。根据图10(a)和图10(b)对比可以看出,当控制律中使用sgn(r)函数时会存在抖振现象,而采用修改后的σ(r)函数,可以削弱抖振现象,使关节控制力矩更加平滑。为进一步对比3种控制算法的动态特性,本文采用关节角跟踪的响应时间(取误差首次为0的时间)、关节角跟踪的最大稳态误差、关节角跟踪的平均稳态误差来评估控制器的性能,6个关节的对比结果如图11所示,具体的仿真数据见表1。

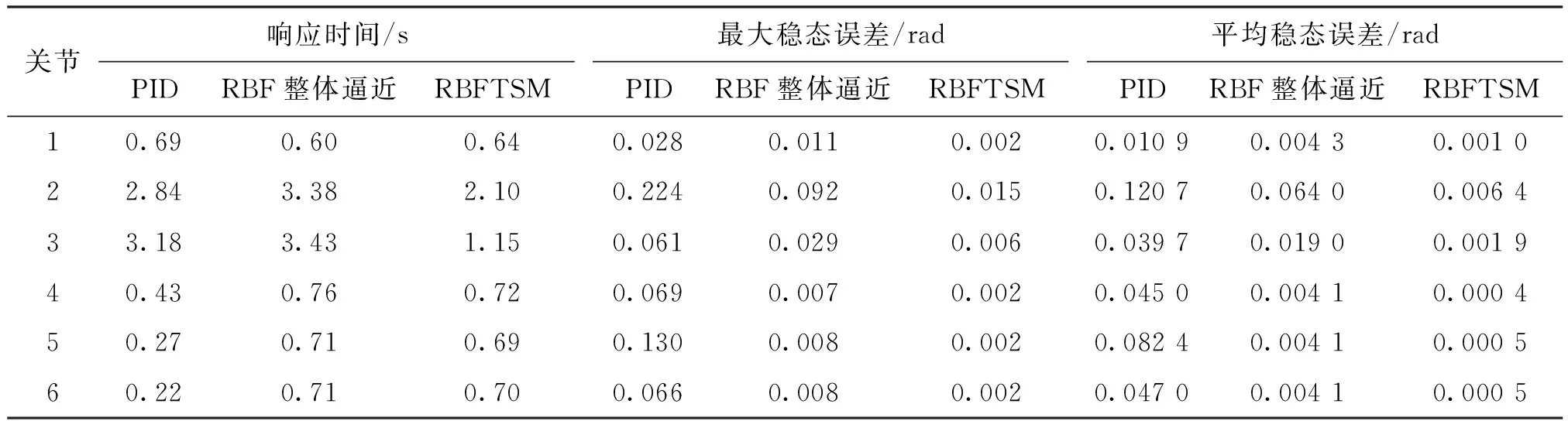
表1 不同控制器关节角跟踪的动态性能仿真数据

分析图11和表1中的数据可知,RBFTSM的性能与传统的PID和RBF整体逼近算法相比有较大提升,控制精度要高于后两种算法。以关节1、2、3为例,RBFTSM与RBF整体逼近算法相比,最大稳态误差分别减小了81.8%、83.7%、79.3%;平均稳态误差分别减小了76.7%、90%、90%。RBFTSM与PID算法相比,响应时间分别缩短了7.3%、26.1%、63.8%;最大稳态误差分别减小了92.9%、93.3%、90.2%;平均稳态误差分别减小了90.8%、94.7%、95.2%。

为测试控制算法的鲁棒性和抗干扰能力,第4s时在末端执行器处添加一个质量时变的负载,其质量呈余弦变化:m=2.5cos(2(t-4))+2.5,t≥4,单位为kg。以关节1、2、3为例,加入负载后关节位置跟踪和误差曲线如图12、图13所示。

由图12、13中可以看到,当加入变化的负载后,PID和RBF整体逼近算法的稳态特性变得较差,误差波动范围增加,鲁棒性不强。与之相比,RBFTSM算法则体现出了较好的鲁棒性。此外,相较于RBF整体逼近算法,RBFTSM算法有更快的响应速度,各关节误差的波动范围更小。对加入干扰后的控制器性能进行评估分析,从结果中可以看出,采用RBFTSM控制算法的机械臂在受到外界干扰后依旧能够保证较好的轨迹跟踪效果。其中关节2最大稳态误差为0.017 rad,关节3最大稳态误差为0.008 rad,其余4个关节的最大稳态误差均在0.002 rad以内;关节2平均稳态误差为0.007 3 rad,关节3平均稳态误差为0.002 8 rad,其余关节的平均稳态误差均在0.000 9 rad以内。与RBF整体逼近算法相比,关节2最大稳态误差减少了85.6%,平均稳态误差减少了90.3%;关节3最大稳态误差减少了81%,平均稳态误差减少了88.6%;其余关节的最大稳态误差减少了81.8%,平均稳态误差减少了79.1%。由上述仿真结果可以看出,该算法具有优异的控制性能。

4 结 论

本文对六轴机械臂的轨迹跟踪控制算法进行了深入研究。主要创新性工作如下:

(1)在Simulink中搭建了六轴机械臂的物理仿真模型,控制律中引入了非奇异终端滑模超曲面;

(2)采用RBF神经网络进行逼近,通过权值自适应律的在线调整,实现动力学模型重构;

(3)与已有研究对比,提高了轨迹跟踪的精度、响应速度和稳定性,在受到外界干扰的情况下,控制器体现出了较强的鲁棒性。

本文研究工作为模型不确定和存在外界干扰与摩擦的六轴机械臂轨迹跟踪控制提供了基础。在未来工作中,考虑引入优化算法,使控制器的参数能够自适应调节,并在真实的机械臂上进行实验验证。