采用数据降维的固态硬盘故障检测方法

王宇菲,董小社,王龙翔,陈维多,陈衡

(西安交通大学电子与信息学部,710049,西安)

近年来,固态硬盘在诸如阿里巴巴、谷歌、微软等大型公司里的普及程度越来越高[1],但是固态硬盘往往只有有限的使用寿命,随着磨损老化最终失效是在所难免的[2-6]。故障检测技术往往能够提前发现问题,保证大规模存储系统的可靠性和可用性,降低数据丢失的风险。不少已有工作针对机械硬盘的故障检测技术进行了研究[4,7-10]。文献[4]开发了一种基于成本敏感排序的机器学习模型,根据硬盘在将来的错误倾向对硬盘故障进行排序分类。Zhang等根据硬盘局部扇区的错误构建了故障检测模型[8]。Xiao等基于在线随机森林提出了硬盘故障预测模型[9]。Wang等基于长短时记忆网络改进了生成对抗网络的结构,通过生成虚拟硬盘故障数据以扩充样本集规模,提高了小样本情况下硬盘故障检测准确率[10]。

然而,由于固态硬盘复杂的特性,只有少数工作基于非公开的数据研究了固态硬盘的故障检测。文献[3]基于随机森林方法研究了不同自我监测分析与报告技术(SMART)特征对固态硬盘故障检测的重要程度。谷歌针对其内部固态硬盘分析了数据特点并构建了故障检测模型[11-12]。Sarkar等基于设备固件功能提供的特征研究了固态硬盘的故障检测技术[13]。

新型固态硬盘通常包含大量的高维SMART数据,这会给众多人工智能算法的效果带来负面影响[14]。降维能够减少原始数据中噪声特征的影响,并突出与数据特点更加相关的特征,提升算法效果[15]。国内外关于传统降维方法的研究主要有主成分分析(PCA)[16]、线性判别分析[17]、奇异值分解(SVD)[18]、遗传算法[19]和因子分析(FA)[20]等。文献[21]利用堆叠自动编码器(AE)对旋转电机的振动谱信号进行降维,提高了旋转电机故障检测准确率。文献[22]基于堆叠自动编码器对农作物监控数据降维,提升了分类精度。文献[23]结合了自动编码器和基于集成思想的分类器提出了一种新的数据降维方法。文献[24]利用自动编码器的降维特性解决了高维地震反演问题。不过这些降维方法多用于处理线性数据,降维后的低维数据通常为原始高维数据的线性组合,在处理高维非线性数据时存在不小的局限性。并且已有工作普遍基于固态硬盘的原始高维SMART数据直接进行分析并结合人工智能算法构建故障检测模型,在模型构建的数据预处理阶段有不小的局限性,存在可优化的空间。

为解决上述问题,本文结合固态硬盘SMART数据的时序特点,基于门控循环单元(GRU)对自动编码器的结构做了改进,提出了一种采用GRU稀疏自动编码器(GRUAE)降维的固态硬盘故障检测方法(GAL)。AE能够在无监督方式下学习数据编码,可以非线性地提取数据中最重要的特征,对于大量高维非线性数据降维效果较好[25]。GAL首先利用固态硬盘数据训练GRUAE模型,在GRUAE模型训练完成后利用其中的编码器作为降维的工具,对固态硬盘的原始高维SMART数据进行降维,减少固态硬盘原始SMART数据中噪声特征的影响并突出与数据特点更加相关的特征,随后基于降维过的低维SMART数据利用长短时记忆网络(LSTM)进行故障检测。实验结果表明,相比于没有采用任何降维手段,GAL使两种闪存类型的固态硬盘故障检测准确率、召回率和F0.5分别提高了4%、5%、4%和4%、8%、5%,分别达到97%、95%、97%和97%、96%、97%。GAL的故障检测准确率、召回率和F0.5分别超出对比方法53%、25%、43%。

1 背景知识

1.1 门控循环单元

GRU通过调节单元内信息流的门控结构可以捕获不同时间尺度的依赖关系,且不需要单独的记忆单元[26]。

(1)

更新门决定了一个单元在t时刻更新多少内容,计算公式如下

(2)

(3)

式中:⊙是基于元素的乘法;rt是一组重置门。重置门计算公式如下

(4)

1.2 自动编码器

AE是一种学习模型,旨在通过无监督学习从数据中提取表示特征。AE的结构包括编码器和解码器两部分,如图1所示。编码器试图从输入数据中提取潜在代码,将输入数据映射到低维特征空间;解码器试图从潜在代码中重构出尽可能接近原始输入数据的数据片段。

编码器和解码器的计算公式如下

h=σ1(WEX+b)

(5)

Y=σ2(WDh+d)

(6)

式中X=[x1,…,xn]表示输入数据;n为该输入数据的维度;σ1和σ2为激活函数;h为隐含层特征向量;WE和WD分别为编码器与解码器的权重参数矩阵,其序列长度与网络层数相关。Y为重构后的向量。AE的目标是使重构误差最小化,计算式如下

(7)

2 GAL方法

在真实环境中,固态硬盘的故障是随着使用时间的推移而逐渐出现的。因此,固态硬盘可靠性特性具有较强的时间相关性。相较于传统线性网络,GRU更善于捕捉样本的时序特点,提取与时间相关的特征。采用GRU作为AE模型的编码器来拟合固态硬盘样本的概率分布函数,使编码器可以更好地学习到固态硬盘SMART数据的时序特性,提取其中的潜在代码,将原始输入数据映射到低维特征空间。同时解码器也采用GRU以便更好地捕捉数据的时序特性,将数据从低维空间重构出原始状态。对于整个AE网络,其输入样本维度与输出结果维度相同,训练网络时的标签就是输入样本自身,即整个网络输入等于输出。当训练结束后,得到的最终结果就是编码器与解码器各自的权重参数矩阵序列,此时再将原始样本依次与编码器的权重参数矩阵序列相乘可得到该数据的低维表示,从而实现高维数据的压缩降维,然后该数据的低维表示即能作为其他处理的输入。GAL方法如图2所示,主要包含GRUAE的训练、降维和故障检测3个部分,分为3个主要步骤。

(1)GRUAE的训练。对于输入的原始数据,训练用于降维的GRUAE模型,通过GRU-编码器对原始输入数据进行编码,在隐含层将输入映射到低维特征空间,如此在保留了原始输入数据特点的基础上实现了数据维度的削减;为确保低维特征空间里的数据编码包含了原始输入数据的特点以及各数据特征之间的联系,随后通过GRU-解码器对隐含层输出解码,将数据从低维状态重构成原始高维状态。在每一轮的训练过程中,采用MSE均方误差+KL散度作为度量方式,通过稀疏惩罚项抑制隐含层神经元的输出,计算该重构输出与原始输入之间的误差,使网络具有稀疏的特性。这样即使隐含层神经元数很多,GRUAE模型仍然可以学习到输入数据的重要特征。

(2)降维。在GRUAE模型训练完成后,取出其中的GRU-编码器作为降维的工具,对固态硬盘数据集中的原始SMART数据进行正则化、归一化等预处理,随后利用GRU-编码器对数据进行降维,将固态硬盘SMART数据映射到一个低维特征空间,以减少原始SMART数据中噪声特征的影响并突出与数据特点更加相关的特征,形成一个新的低维数据集。

(3)故障检测。由于固态硬盘SMART数据时序特性较强,而LSTM善于捕获样本的时序特性和提取时间相关特征。鉴于此,基于降维过的低维数据集,采用LSTM进行故障检测,输出诊断结果。

2.1 GRUAE模型

对于模型的结构,如果隐含层包含的节点多于输入层,则会影响AE学习特征的能力。因此,在隐含层节点中加入了稀疏惩罚项作为约束,通过抑制隐含层神经元的输出,使网络达到了稀疏的效果。这样即使隐含层神经元数多,AE仍然可以学习到输入数据的重要特征。

编码器过程表达式如下

h=fθ(x)=AE(Wx+b)

(8)

编码器的参数集表示为:θ={W,b};W为权重矩阵;b为偏移向量;AE是编码器的激活函数。相似地,重构输出表示为

z=gθ′(h)=AD(W′h+b′)

(9)

解码器的参数集表示为:θ′={W′,b′};W′为权重矩阵;b′为偏移向量;AD是解码器的激活函数。因此,损失函数定义为

(10)

假设aj(x)表示隐含层中第j单元的激活量,则第j单元的平均激活量为

(11)

(12)

(13)

添加了稀疏惩罚项的GRUAE模型的优化目标函数定义如下

(14)

式中:λ为权重衰减系数;nl为神经网络层数;Sf为第f层的神经元数;Sf+1为第f+1层的神经元数;Wij(f)表示第p层神经元i和第f+1层神经元j之间连接关系所关联的参数。在模型训练的反向传播阶段,需要计算当前输入数据和输出数据之间的误差,以及除输出层之外的每一层网络里神经元的误差以更新网络参数(W,b)。因此,包含了稀疏惩罚表达式的损失函数表示为

Jsparse(W,b)=J(W,b)+βR

(15)

式中:β为稀疏惩罚系数,本文实验设置为3。

对于输入的原始高维固态硬盘SMART数据,初始化网络的参数,在每一次迭代中,前向传播过程首先计算出隐含层输出结果,然后根据隐含层结果计算出输出层结果;反向传播过程通过Adam方法更新网络参数,以最小化添加了稀疏惩罚项的损失函数,反复循环直至收敛。GRUAE模型训练过程的伪代码如下。

输入 数据样本;Epoch;Batch

输出 GRUAE模型

1 初始化网络权重W

2 初始化网络偏置b

3 fore=1 to Epoch do

4 for batch_number=1 to Batch do

5 计算重构约束矩阵

6 计算局部约束矩阵

7 fork=1 toKdo

8 前向传播过程

9 计算目标约束矩阵

10 反向传播过程,优化目标

11 更新网络参数

12 if loss不再下降 then

13 停止训练,返回结果

14 end if

2.2 降维

2.3 LSTM模型

LSTM通过定义和维护单元状态来调节信息流以获取长期的时间依赖性。存储单元状态Ct-1与中间输出ht-1和随后的输入xt相互作用,以确定内部状态向量的哪些元素应该根据前一时间步的输出和当前时间步的输入进行更新、维护或消失。LSTM的计算公式如下

it=σ(xtUi+ht-1Wi)

(16)

ft=σ(xtUf+ht-1Wf)

(17)

ot=σ(xtUo+ht-1Wo)

(18)

(19)

(20)

ht=tanh(Ct)*ot

(21)

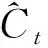
3 数据集概览与预处理

3.1 数据集概览

本文实验选用了来自阿里巴巴的固态硬盘数据集[27]。该固态硬盘数据集包含了固态硬盘的SMART数据和诸如时间戳、设备序列号等基本信息。需要注意的是不同厂家提供的SMART参数可能会不一样,并且某些参数会因为设备类型不同而代表不同的含义。因此,提取了数据集中数据记录较完整并且Flash类型为MLC和3D TLC的两个型号的固态硬盘在2019年全年内的数据进行实验测试。两种固态硬盘的型号分别为MA2和MC1,数据的基本信息见表1,其采样间隔均为1天。

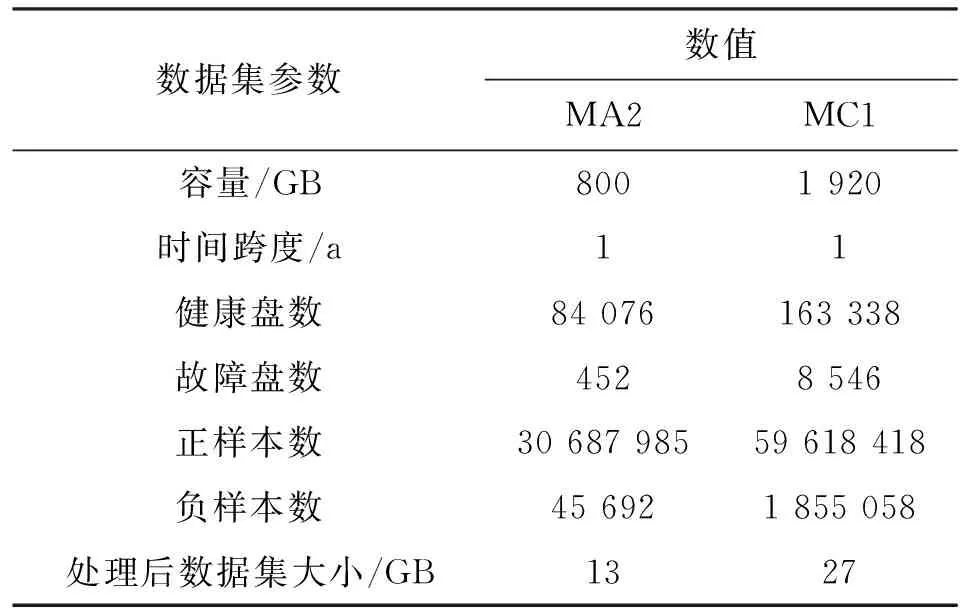
表1 MA2、MC1数据集的基础参数

3.2 参数信息和预处理

数据集中的SMART数据包含Raw值(Raw)和Normalized值(Norm)两种赋值种类,其中的Norm是根据厂家非公开的自定义公式由Raw计算而来。因为有些Norm可能会损失一些数据精度,而其对应的Raw对于固态硬盘的健康变化可能更为敏感,所以同时采用了Raw(R)和Norm(N)作为实验参数,MA2和MC1两种型号的固态硬盘包含的SMART参数信息及其赋值类型见表2。

不同SMART参数的单位不一样,参数值所跨的范围差别也很大,为了保证不同参数权重的公平性,采用参数尺度缩放对数据进行归一化,公式如下

(22)

式中:x是参数的原始值;xmax和xmin分别为该参数的最大值和最小值。

4 实验结果

实验使用了准确率、召回率和F0.53个指标来衡量不同机器学习算法检测故障的效果。从实践经验来看,一旦一个固态硬盘被判定为故障,不管判定正确或错误,管理员将停止使用该固态硬盘以进行进一步检查。鉴于将一个健康的固态硬盘判定为故障所造成的代价远远大于将一个可能故障的固态硬盘错误地判定为健康。因此,本文实验采用F0.5代替F1,使准确率的重要程度为召回率的两倍。相关定义如下

(23)

表2 MA2、MC1数据集包含的SMART参数名称及其赋值类型

(24)

(25)

式中:TP为真阳性;FP为假阳性;FN为假阴性。

实验将数据集中的数据分别按照7∶3的比例随机划分为训练集与测试集进行测试。GRUAE模型的编码器为具有1个隐含层的GRU,输入层的单元数与对应型号固态硬盘SMART数据的维度相等,隐含层有10个单元,时序长度为3,输出层单元数为10,dropout设置为0.2;解码器为具有1个隐含层的GRU,输入层单元数为10,隐含层单元数为10,输出层有线性映射并采用tanh作为激活函数,输出层的单元数与对应型号固态硬盘SMART数据的维度相等,dropout设置为0.2,学习率为0.001。

LSTM的结构包含输入层、两层LSTM隐含层以及输出层,输出层有线性映射,采用Sigmoid作为激活函数。输入层的单元数为降维后的固态硬盘SMART数据维度,隐含层单元数为100,输出层单元数为1,dropout设置为0.2,学习率为0.001。

GRUAE模型中编码器的输出层单元数为10,即为降维后的数据维度大小,在确定该数据维度大小时,利用PCA方法,设定主成分占投影特征的方差比例为99%,即包含的主成分对原变量能够解释99%,自动计算得出该数据维度大小。

训练过程中的优化器为Adam。图4给出了训练过程中GRUAE模型在MA2和MC1两个固态硬盘数据集上损失的变化过程。可以观察到,经过一段时间的训练,模型的损失已经下降至接近0并稳定下来,表明模型的训练已经收敛。

实验针对MA2和MC1两个型号的固态硬盘数据,分别训练了各自的GRUAE模型,随后基于GRUAE模型对固态硬盘SMART数据进行降维操作。基于降维后的数据,对比了多层感知器(MLP)、随机森林(RF)、逻辑回归(LR)、决策树(DT)、支持向量机(SVM)、GRU和本文方法7种人工智能算法的故障检测的效果,并且与文献[23]的方法进行了比较。

实验所用平台为一台高性能服务器,具体配置如下:两个Intel Xeon E5-2620 v4 @ 2.10 GHz处理器、94G DDR4内存、4TB存储空间。在软件方面,服务器安装了Ubuntu 18.04.5 LTS操作系统,其内核版本为Linux version 4.15.0-171-generic,编译器版本为gcc version 9.3.0。方法实现基于PyTorch 1.7.1和scikit-learn 0.24.1。

4.1 MA2数据集结果

MA2的准确率如图5所示,在没有采用任何降维手段的情况下,GRU和LSTM两个在处理时序数据方面具有优势的深度学习算法要明显好于其他5种传统机器学习算法。在进行降维后,对于所有算法来说,准确率基本都有或多或少的提升。其中MLP和DT的提升幅度较大,平均接近20%,其他方法的提升相对MLP和DT来说稍低一些,RF和SVM的提升幅度分别为6%和13%。对于LR,降维带来的提升效果不太明显,平均提升效果不到3%。虽然GRU与LSTM的基础效果已经比较出色了,但是降维依旧可以带来3%～4%的提升。并且由于LSTM本身的网络结构比GRU复杂,因此效果也稍微好一点。本文所提方法GAL即GRUAE+LSTM的准确率超过了97%,是所有方法里最好的一个。

MA2的召回率如图6所示,与准确率类似,在没有采用任何降维手段的情况下,GRU和LSTM两个在处理时序数据方面具有优势的深度学习算法要明显好于其他5种传统机器学习算法。在进行降维后,有些算法的召回率有很大的提升,例如DT,平均提高幅度将近40%;也有一些算法的提升效果比较微小,例如LR和SVM,平均提升幅度大约为3%。MLP、RF、GRU以及LSTM的提升效果比较接近,平均增幅为5%左右。同样地,尽管GRU和LSTM的基础效果已经比较出色了,但是本文的GRUAE降维依旧可以提升其召回率,并且本文所提方法GAL的表现依然是所有方法里最好的一个。

MA2的F0.5如图7所示,整体趋势与准确率相似,在进行降维后,多种算法的效果基本都有提升,整体来说,MLP、DT和SVM的相对提升幅度较多,平均在15%左右。GRU和LSTM的效果非常接近,均好于其他算法。由于本文所提方法GAL的准确率和召回率在所有方法中均为最好,因此其F0.5也是最好的一个。

4.2 MC1数据集结果

MC1的准确率如图8所示,与MA2的准确率类似,GRU和LSTM在处理时序数据方面具有优势的深度学习算法要明显好于其他5种传统机器学习算法。相比于没有降维的时候,降维后基本所有算法都有提升,其中RF的提升效果尤为明显,平均提高了约35%。MLP、DT和SVM的提升幅度也比较可观。对于MLP、DT、SVM、GRU和LSTM来说,准确率分别提升了6.5%、8.5%、12.5%、4%和4%。虽然GRU和LSTM作为基础效果最好的两个方法,准确率分别为92%和94%,但是经过GRUAE的降维其准确率依旧能够得到提升,其中LSTM的效果稍好于GRU。本文所提方法GAL作为整体效果最好的方法,准确率几乎达到了98%。

MC1的召回率如图9所示,在不采用任何降维手段的情况下,GRU和LSTM依然是基础效果最好的方法,原始召回率分别达到了90%和91%;DT在5种传统机器学习算法中效果最好,原始召回率为56%。在进行降维后,DT依然是提升幅度最大的算法,平均提高幅度将近20%;也有一些算法的提升效果比较微小,例如LR和SVM,幅度不到3%。经过GRUAE降维后GRU和LSTM的召回率均提高了5%左右,达到了95%和96%,因此本文所提方法GAL的效果依旧最好。

MC1的F0.5如图10所示,整体趋势与准确率相似,在进行降维后,多种算法的效果基本都有提升,经过GRUAE降维后,MLP、DT和SVM的相对提升幅度最多,平均在9%左右。由于本文所提方法GAL的准确率和召回率在所有方法中均为最好,因而其F0.5也是最好的一个。

4.3 与WEFR的对比结果

为进一步评估本文所提方法GAL效果,对比了文献[27]所提的WEFR方法。因为GAL方法基于GRU改进了传统AE的结构,使GRUAE模型的编码器可以更好地学习到固态硬盘SMART数据的时序特性,提取其中的潜在代码,减少固态硬盘原始高维SMART数据中噪声特征的影响并突出与数据特点更加相关的特征,将原始输入数据映射到低维特征空间。因此,经过GRUAE模型降维处理,多种人工智能算法的故障检测效果得到了较好地提升。

如图11和图12所示,在MA2数据集上WEFR的准确率、召回率和F0.5分别为57%、32%和49%。除了RF和LR,其他方法基于GRUAE降维后都达到了更好的效果,效果最好的LSTM的准确率、召回率和F0.5分别为97.8%、95%和97%,分别超过WEFR 40.8%、63%和48%。在MC1数据集上WEFR的准确率、召回率和F0.5分别为49%、18%和36%。基于GRUAE降维后的所有算法的效果均好于WEFR,效果最好的LSTM的准确率、召回率和F0.5分别为97%、96%和96.8%,分别超过WEFR48%、78%和60.8%。因为固态硬盘的SMART数据时序特点较强,而WEFR基于随机森林方法,在处理时序数据时存在一定的局限性,所以整体准确率和召回率有不少可提升的空间。

实验结果表明,GRUAE模型可以学习固态硬盘SMART数据的时序特点,对固态硬盘原始高维SMART数据进行降维,在保证降维后的数据包含了原始数据特点的情况下,提高了多种人工智能算法的故障检测准确率。在两个型号的固态硬盘数据集上,相比于无降维情况下的固态硬盘故障检测,GAL使检测的准确率、召回率和F0.5分别提高了4%、5%、4%和4%、8%、5%。相较于其他方法,GAL的检测准确率、召回率和F0.5超出了53%、25%、43%。并且,GAL在多种评价指标方面均给出了最好的效果,充分说明了方法的有效性。

5 结 论

为解决固态硬盘SMART数据的高维性对传统机器学习算法故障检测效果带来的负面影响,本文结合GRU与AE提出了一种基于GRU稀疏自动编码器降维的固态硬盘故障检测方法GAL。首先通过学习固态硬盘SMART数据的特点训练GRUAE模型,随后利用GRUAE模型中的编码器对高维固态硬盘SMART数据进行降维,提取其中的潜在代码,减少固态硬盘原始SMART数据中噪声特征的影响并突出与数据特点更加相关的特征,随后基于降维后的低维SMART数据利用LSTM进行固态硬盘故障检测。实验结果表明,相比于没有采用任何降维手段,GAL使两种闪存类型的固态硬盘故障检测准确率、召回率和F0.5分别提高了4%、5%、4%和4%、8%、5%,分别达到97%、95%、97%和97%、96%、97%。GAL的故障检测准确率、召回率和F0.5分别超出WEFR对比方法53%、25%、43%。在未来的工作中将优化LSTM模型架构,进一步改进所提方法,提高检测性能。