智能垃圾车箱体结构焊接变形数值预测及控制
徐丽平
(黎明职业大学,福建 泉州 362000)
焊接过程复杂且不可逆,焊接变形直接影响产品质量、结构强度以及后续的装配和组装工序。多年来,诸多国内外专家学者利用有限元分析数值模拟方法预测焊接变形,研究控制残余应力和减小焊接变形、提高焊接质量的工艺[1-4],但缺少对组装部件多、精度要求较高的大型平行焊缝箱体结构件的焊接变形预测及顺序优化。
智能垃圾车要求装卸自动化程度高、装载能力强、结构强度高、密封性能好、工作过程可靠。大箱体框架是智能垃圾车的基础和关键结构之一,由多个冲压型板拼焊而成,其特点是尺寸大、焊缝多、单条焊缝长,而型板冲压后存在内应力,极容易使得长直拼缝由于焊接热效应而出现过大的焊接变形。框架焊接完成后需与前面板、顶梁、压缩缸、油缸支座、导流板等其他结构件进行装配和组装,因此箱体框架的焊接变形将影响全车的组装和质量,过大的焊接变形增加后续矫正和修补的工序,影响生产的正常周期,造成一定程度上的浪费和经济损失。同时,高残余应力的存在可诱发热裂纹、冷裂纹等,容易引起疲劳破坏,致使整个结构失效[5]。焊接顺序对最终的焊接变形影响极大,在生产中如果逐个顺序试验,会增加巨大的生产成本和时间成本。因此,需要进行焊接的数值模拟计算、优化焊接顺序,在焊接过程中能精确减少焊接变形,增加焊接结构的可靠性,为后续的设备组装提供焊接品质保障。
1 箱体有限元模型建立
1.1 箱体有限元模型
箱体由6 块厚度为8 mm 的Q345 低合金高强钢板组合焊接而成,总体尺寸为4 000 mm×2 370 mm×1 800 mm,共有6 条纵向平行长焊缝,焊接后车厢一端为平端,一端为坡口端。
对箱体进行分块有限元建模及网格划分,采用热-力耦合算法对焊接结构进行研究。由于箱体模型尺寸大,考虑到焊接时塑性变形主要集中在焊缝及热影响区周围的狭小区域内,整体网格采取疏密结合的方式划分,焊缝及其热影响区域采用较密集网格,距离焊缝较远及温度影响较小的区域采用较稀疏网格[6]如图1 所示。为保证计算精度,整个车厢在网格划分上全部采用八节点六面体实体单元,模型单元数为120 384个,网格数为282 016。计算过程中材料假定为各向同性,不考虑焊缝熔池内部的化学反应及搅拌、对流,划分网格后的箱体有限元模型及6 条焊缝编号如图2 所示。
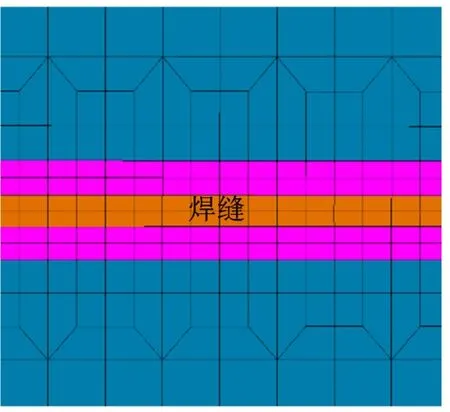
图1 疏密结合网格示意图

图2 车厢整体有限元模型
1.2 焊接顺序设计
由于斜坡口端的存在,使得箱体上下结构不对称,因此不同的焊接顺序将对每一块钢板的焊接变形都会产生不同程度的影响。本次仿真设计出3 种焊接方案:(1)顺时针方向的顺次施焊;(2)以对面相对的焊缝为一组先后施焊;(3)以对面交叉的焊缝为一组先后施焊。焊接方案及具体施焊顺序如表1 所示。

表1 焊接方案及具体施焊顺序
1.3 材料特性
箱体母材材质为Q345 低合金高强钢,该钢材具有较优秀的焊接性能,其热导率等热物理参数及力学参数如表2 所示。
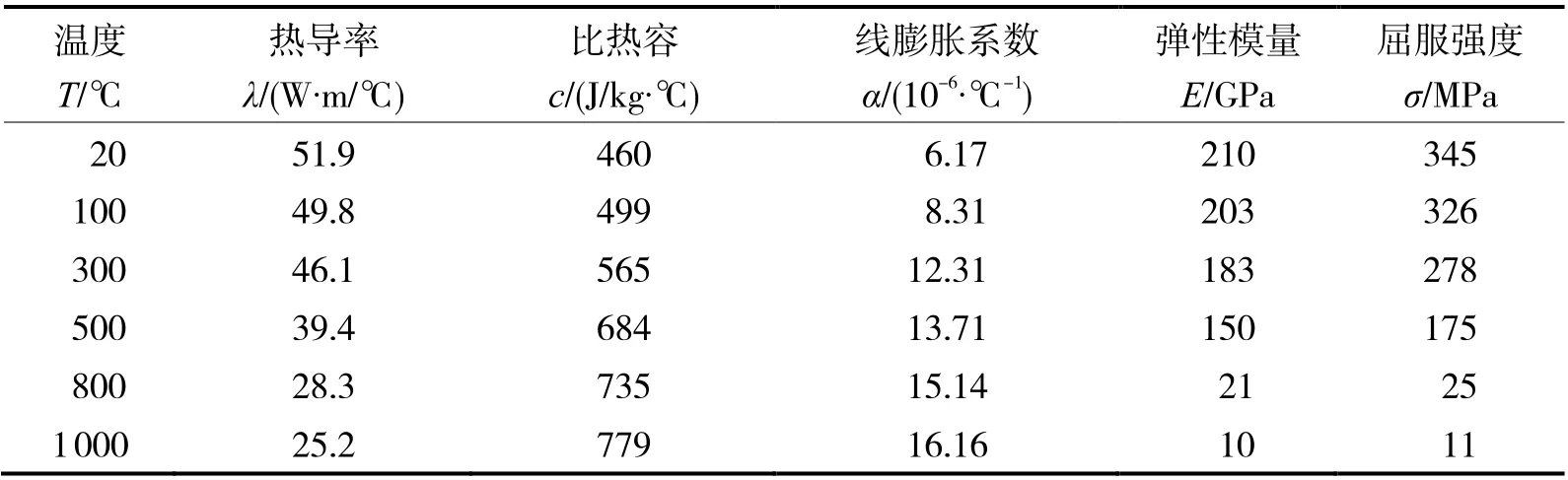
表2 不同温度下Q345 低合金钢热物理及力学性能参数[7-9]
2 热源模型及温度场计算
焊接时高度集中的热源具有移动的特点,形成对时间和空间梯度都很大的瞬态温度场,而这种不均匀温度场是影响焊接应力与焊接变形的重要因素,因此,焊接热源模型的建立与焊接温度场的模拟是焊接数值模拟的重要部分[10-11]。智能垃圾车箱体的焊接方法为混合气体保护焊,电流80~120 A,电压18~20 V,气体流量10~12 L/min,在模拟温度场计算时,采用Goldak 提出的双椭球热源模型[12]。该模型充分考虑了热源移动对热流分布的影响,能准确模拟焊接过程中热源前端温度变化快而后端温度变化慢的特点,并将其转化为在时间域和空间域上作用于箱体焊件的数学表达式[13]。双椭球热源模型前后椭球的热分布函数分别为
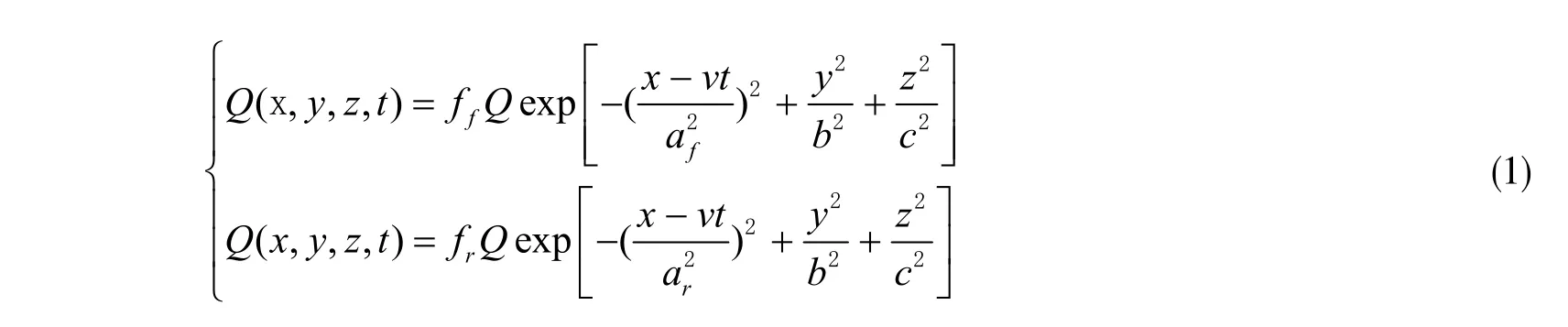
式(1)中,Q(x,y,z,t)代表时间t在(x,y,z)位置的热流量;ff,fr分别为前、后两个椭球的能量输入;v是焊接速度;a f,ar,b,c为高斯参数;a f,ar分别为前、后半部分椭球的长度;b为熔宽;c为熔深[14]。
由于焊接的热分析过程是一个典型的非线性瞬态过程,因此可用非线性传热方程来描述[15]:
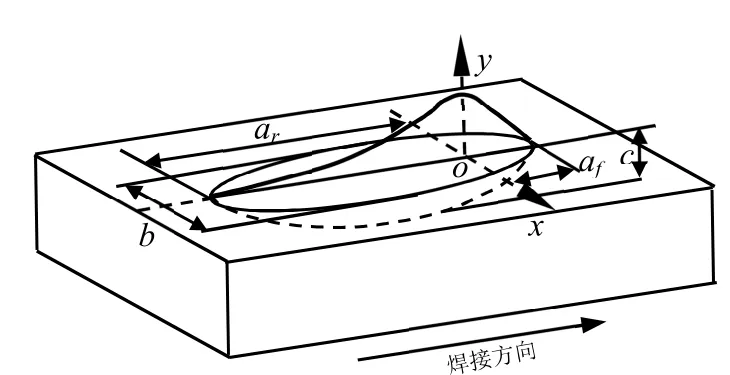
图3 双椭球热源模型
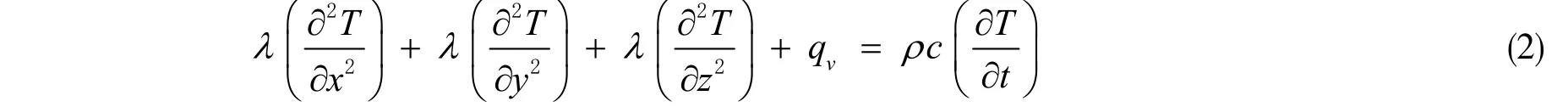
式(2)中,ρ为材料的密度(g/mm3);c为材料的比热容(J/g∙℃);qv为内部热源发热率(W/mm3);λ为导热系数。考虑模型与外部环境的对流与辐射,通过完全牛顿法来描述模型与外部空气的对流散热:

式(3)中,cq为对流散热量,ch为对流散热系数,取值3.4×105(W/(mm2∙℃));sT为模型表面的温度;0T为外部环境温度,设为20 ℃。产生的辐射损失量问题,采用Stefan-Boltzmann 定律来定义[16]:
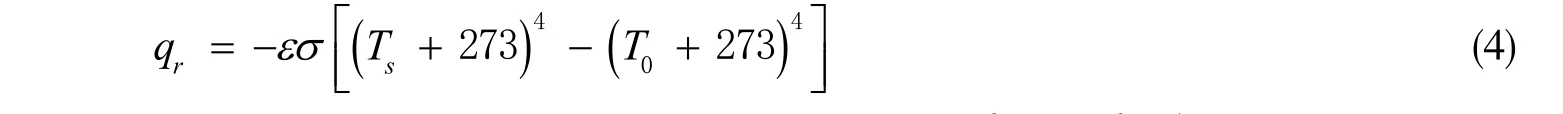
式(4)中,qr表示为热辐射损失量;σ为Stefan-Boltzmann 常数,取值56.7×10-8W∙m-2∙k-4;ε为热辐射率,取值0.8。
3 焊接变形结果分析
参考表2 设置模型材料力学特性参数并定义材料属性,将温度场模拟所求的温度变化ΔT细化为若干增量,逐个加载到箱体有限元单元中,对箱体模型进行焊接变形仿真计算。各单元的应变增量{dε}e与位移增量{dδ}e的表达式为

材料热弹塑性变形应力σ应变ε和温度T之间的表达式为

式(5), (6)中,[B]为几何单元矩阵;[D]为弹性矩阵;{C}为关于温度T的函数,通过各单元的模拟计算,焊接仿真完成后变形量能以云图和数值展示[11]。
经过分析对比14 组焊接仿真计算结果,焊接变形主要在焊缝区,3 种施焊方案的x向变形总体差异较小,并且x正向位移的峰值都位于起弧点,x负向位移的峰值都位于收弧点;但不同施焊方案和施焊顺序对y向和z向变形分布差异较大。1-2-3-4-5-6 施焊顺序变形云图如图4 所示,不同焊接顺序各向变形数据如表3 所示。
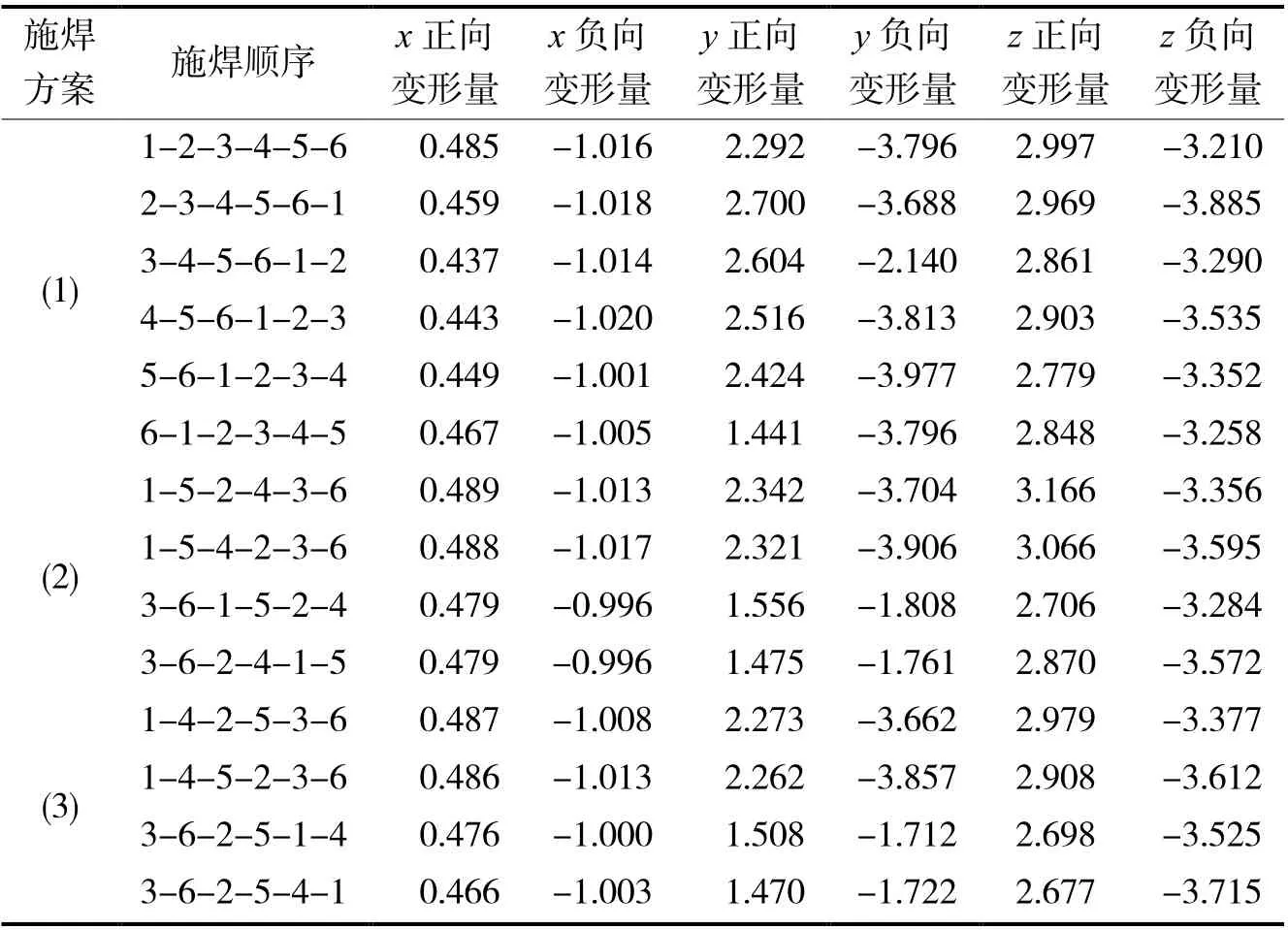
表3 不同焊接顺序各向变形量 mm

图4 焊接顺序1-2-3-4-5-6 三方向变形云图
3.1 顺次施焊变形分析
从顺次施焊的各顺序、各方向变形云图图4 可以看出,顺次施焊不同焊接顺序下,x正向最大变形量为0.485 mm;x负向最大变形量为1.02 mm;y向和z向变形分布图具有较大的差异,y向大变形区位于左、右侧壁的焊接中心区域,z向变形主要存在于上、下板。
焊接顺序为“2-3-4-5-6-1”时,y正向变形峰值最大为2.70 mm,“6-1-2-3-4-5”的y正向变形峰值最小为1.441 mm,减小了46.63%的y正向变形;“5-6-1-2-3-4”的y负向变形峰值最大为3.977 mm;“3-4-5-6-1-2”的y负向变形峰值最小为2.14 mm,减小了46.19%的y负向变形;焊接顺序“3-4-5-6-1-2”的y正负向综合变形最小。不同焊接顺序对z正向变形的影响比对z负向变形小。“1-2-3-4-5-6”的z正向变形(上翘变形)峰值最大为2.997 mm;“5-6-1-2-3-4”的z正向变形峰值最小为2.779 mm,减小了7.27%的z正向变形;“2-3-4-5-6-1”的z负向变形(下凹变形)峰值最大为3.885 mm;“1-2-3-4-5-6”的z负向变形峰值最小为3.210 mm,减小了17.37%的z负向变形。焊接顺序“3-4-5-6-1-2”的z正负向综合变形最小。
经过变形量数据及变形云图对比分析,焊接顺序“3-4-5-6-1-2”的综合变形量相对最小,相对其它顺次焊接顺序表现更优。
3.2 对面相对焊缝施焊变形分析
对面相对焊缝先后施焊变形结果显示,以“3-6”作为优先焊接焊缝(即优先对两个侧壁的焊缝3、焊缝6 进行焊接)时,各向变形量均要小于以“1-5”作为优先焊接焊缝的变形量,故以相对面顺序焊接时,应先对两侧壁的焊缝施焊,再对上下壁的4 条焊缝进行相应顺序施焊。对面相对焊缝施焊各顺序下,x正向最大变形量为0.489 mm;x负向最大变形量为1.017 mm,焊接顺序对x向变形的影响较小。焊接顺序为“3-6-2-4-1-5”时y正向最小变形量为1.475 mm,相对减少37.02%;y负向最小变形量为1.761 mm,相对减少54.92%。焊接顺序为“3-6-1-5-2-4”时,z正向最小变形量为2.706 mm,相对减少14.53%;z负向最小变形量为3.284 mm,相对减少8.65%。
经过对变形量数据及变形云图综合分析,“3-6-1-5-2-4”的焊接顺序表现更优。
3.3 对面交叉焊缝施焊变形分析
对面交叉焊缝进行施焊的4 组焊接顺序中x向位移云图变形规律与顺次施焊、对面相对焊缝先后施焊的变形规律基本相同,在各施焊顺序中,x向总体变形量较小。通过y向位移云图和z向位移云图,可以发现其影响规律与对面相对焊缝焊接相似,同样是“3-6”为优先的焊接顺序表现更佳。且在“3-6”为优先的两种情况中,上下壁焊接顺序为“3-6-2-5-1-4”与“3-6-2-5-4-1”的y向位移及z向位移表现几乎相同,故上下壁的交叉焊接顺序对y向位移、z向位移影响较小。且在相同对面情况下,交叉焊缝各焊接顺序的y向位移变形量、z向位移变形规律与相对焊缝先后施焊几乎相同,故是否交叉施焊对y向变形及z向变形影响不大。
3.4 形变曲线图比较
3.4.1 形变数据提取路径选择
对顺次施焊、对面相对焊缝、对面交叉焊缝3 种施焊方案的各组模型进行x,y,z向形变的数据提取。各路径提取情况分类见图5,箭头所示为提取路径。3 种施焊方案均提取x,y,z向形变数据,其中x向形变中,路径j,k分别是前端口与斜坡口的四条边,口字形周长;y向形变中,路径e,g是两侧壁的竖向中线,路径f,h是斜坡口中两侧壁的直线(顺次施焊不提取斜坡口处路径);z向形变的路径中,路径a,c是上下表面的竖向中线、路径b,d是上下表面的横向中线。
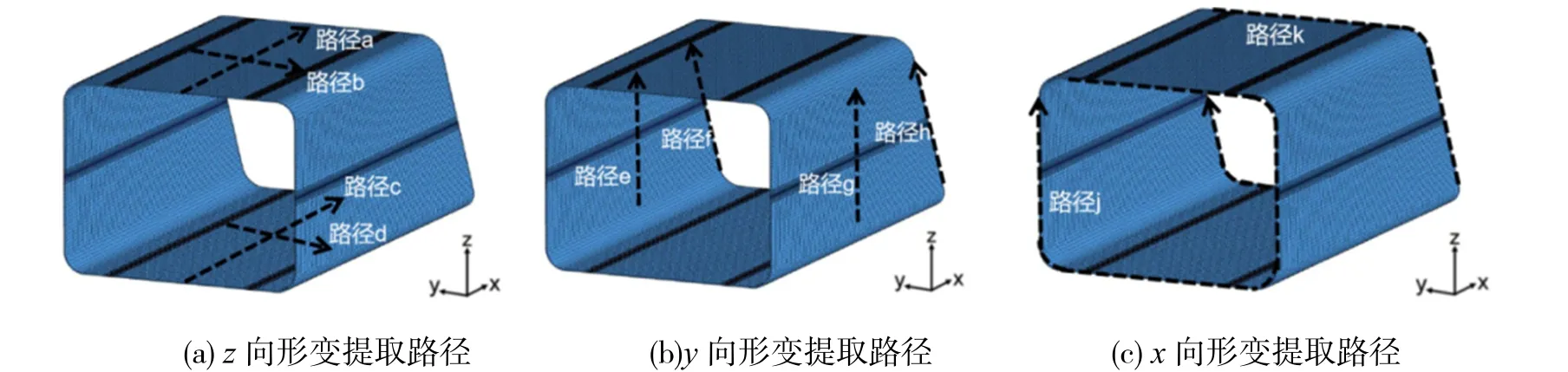
图5 3 方向形变提取路径
3.4.2 各向形变曲线图比较
从3 种施焊方案的各路径形变曲线图可以看出,顺次施焊各顺序形变规律基本相似,没有形变表现比较突出的顺序,且形变量相对另两种方案更大;对面交叉焊缝施焊方案中,各组的形变规律与对面相对焊缝施焊的形变规律基本相似,侧壁先施焊的顺序表现更加。
对面相对焊缝方案的各组形变曲线图如图6~8 所示,通过对比可以看出,不同的施焊顺序对形变量产生影响,特别是在y,z方向的形变。结合上文变形云图分析,在y向形变曲线图中,优先施焊“3-6”两侧壁的形变量明显小于优先施焊“1-5”上下表面的形变量,采用相对面优先施焊两侧壁的方案合理;再结合z向形变曲线图,“3-6-1-5-2-4”的四条形变路径的形变综合表现要优于“3-6-2-4-1-5”,故对面相对焊缝施焊的最佳顺序为“3-6-1-5-2-4”。
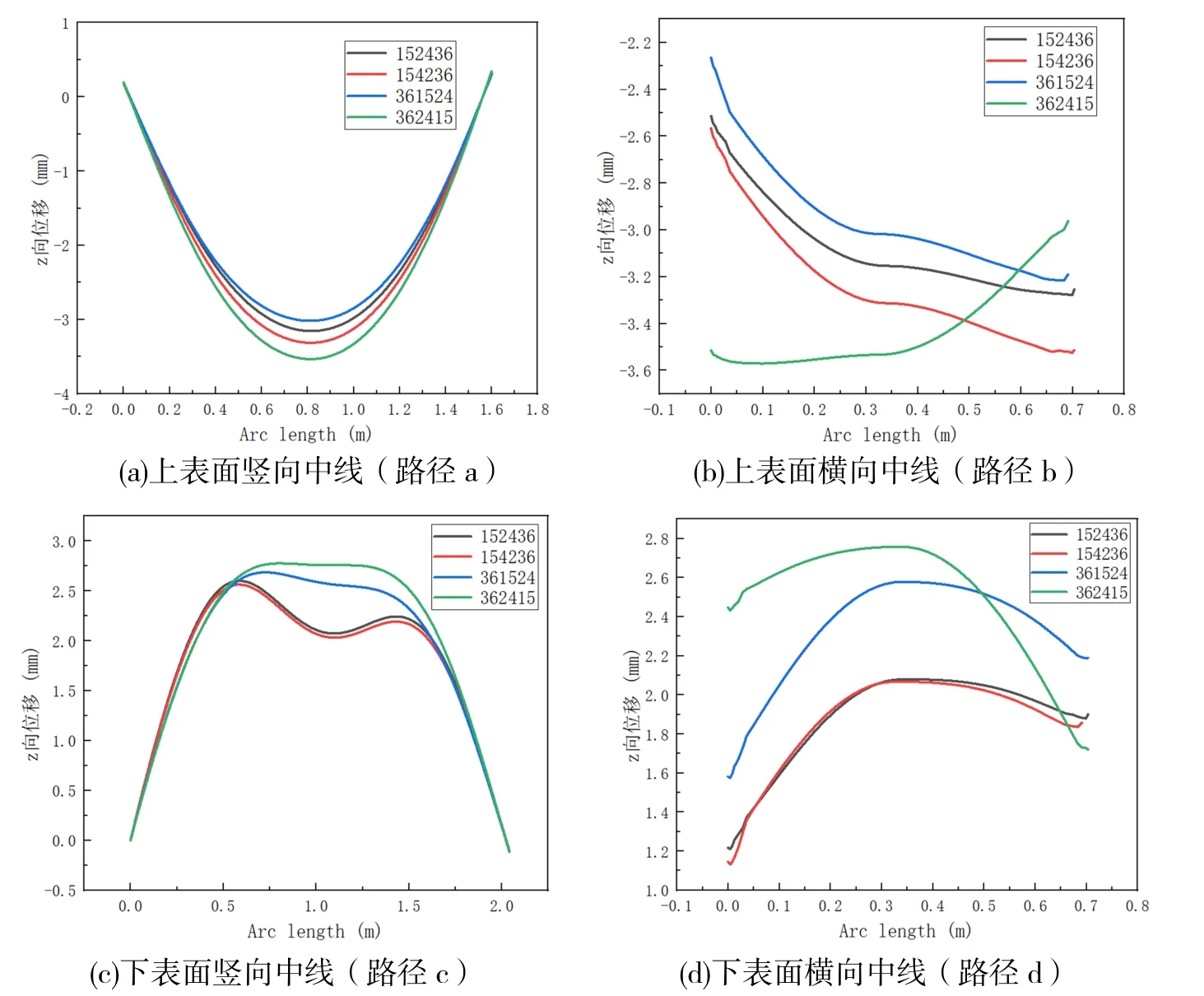
图6 对面相对焊缝施焊z 向形变曲线比较

图7 对面相对焊缝施焊y 向形变曲线比较
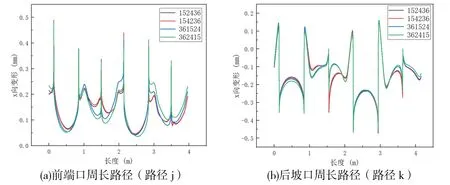
图8 对面相对焊缝施焊x 向形变曲线比较
4 结论
通过对智能垃圾车箱体结构的有限元数值模拟,并对3 种施焊方案的各焊接顺序形变量及残余应力对比,本文得出以下结论:(1)相对面施焊以及相对面交叉施焊,比顺次施焊更具优势,总体形变量更小;(2)在相对面施焊与相对面交叉施焊的对比中发现,是否交叉施焊对各向形变量影响较小,实施交叉施焊的必要性不大;(3)结合变形云图和形变曲线图,对比得出采用对面相对焊缝施焊方案的“3-6-1-5-2-4”是最佳焊接顺序。故“3-6-1-5-2-4”可以作为总体方案的最佳焊接顺序。
实践生产证明,优化后的焊接顺序能有效控制箱体焊接变形,实际测量误差与数值预测计算在15%以内,为设备组装提供了可靠和稳定的尺寸精度,有效节约生产成本。

