基于GARCH-EVT 模型的我国创业板市场风险分析

胡若尔，芦雪娟

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

纵观国内外创业板市场的相关研究成果，国外学者更多的是在理论层面的探究和探讨，比较了多种建模方法在不同条件下的使用效果，研究体系更为完善；而国内的学者在理论层面的创新较少，更侧重于模型在不同领域的应用与实证分析，对模型的实用性研究更为深入。阅读大量文献后可以发现，在研究对象的选取上，绝大多数学者在研究股票风险时，普遍都会选择主板市场进行研究和分析；在模型选取上，较多的专家与学者在研究创业板市场时还是使用传统的GARCH-VAR 模型。GARCH 模型能够很好地消除序列的相关性和异方差性，极值理论（EVT）又可以有效刻画极端序列的尾部特征，GARCH-EVT 的组合模型对波动性和极端风险的优良拟合效果已经得到了的证实。因此，本文主要以创业板为分析对象，尝试利用GARCH-EVT 组合模型进行创业板风险度量研究，并与传统的方法进行比较分析。

1 数据选取与预处理

本文选取了我国深圳证券交易所编制的创业板综合指数（简称创业板综，编码399102）自2015 年10月至2021 年9 月，共1 461 个交易日的日收盘价数据进行后续的研究。数据来源为同花顺iFinD 数据库。在开始分析之前，先要将数据预处理，这里将先计算出创业板综的日对数收益率，计算公式为

其中，ᵄᵆ为指数在ᵆ日的收盘价，ᵄᵆ−1为指数在ᵆ−1日的收盘价，以同样的方法最终得出3 个指数的日对数收益率，下文中简称收益率。

2 描述性统计分析

首先，通过Python 软件对创业板综指的对数收益率序列进行描述性统计分析，得到如图1 所示结果。

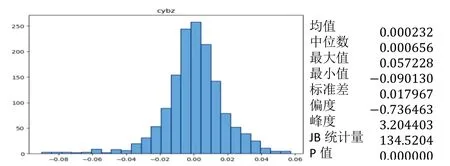
图1 创业板综描述性统计分析结果

可以很清晰发现，创业板日对数收益率的平均数为0.000 232。标准差是0.017 967，标准差反映了所统计数据的离散程度，标准差的数据较大，可以由此得出创业板市场波动性也很大。从偏度的角度来看，数值为-0.736 463，该数值小于0，证明数据是日对数收益率序列是左偏分布的，图中的峰度为3.204 403，大于正态分布的峰度值3，JB 统计量为134.520 4，相应概率为0。从上述的一系列数值中充分说明创业板的收益率并不服从正态分布，具有尖峰厚肥尾的特点，也说明了创业板市场有较大风险。

3 波动性估计

在建立波动率模型之前，首先需要对数据的平稳性进行检验，若数据不平稳，则需要对原数据进行差分或其他处理方式使其达到平稳。创业板综指的ADF 检验t 统计量为-38.504 3，均小于其在1%, 5%与10%显著性水平下的临界值，而且检验的P值为0。以上数据说明该检验结果是显著的，拒绝原假设，即认为创业板综指的日对数收益率序列都是显著平稳的，可以进行后续的研究。

接着将序列的平方值作为波动率的代理变量，通过LB 检验来检验残差平方序列的自相关性。该检验的结果显示P值为2.61e-58，可以拒绝原假设，即证明了原序列存在ARCH 效应，因此可以建立GARCH模型。

可以在Python 中使用ARCH 包或者R 语言中使用fGarch 程序来进行建模，同时拟合GARCH(1,1),GARCH(1, 2), GARCH(2, 1)与GARCH(2, 2)模型，根据信息准则分析结果，随着参数增加，模型的AIC、BIC 等值并没有显著增加。因此证明还是选择使用最简洁的GARCH(1,1)模型最合适。用其拟合创业板综指的日对数收益率序列，其参数的拟合结果如表1 所示。

根据表1 中显示的函数返回值，模型结果为

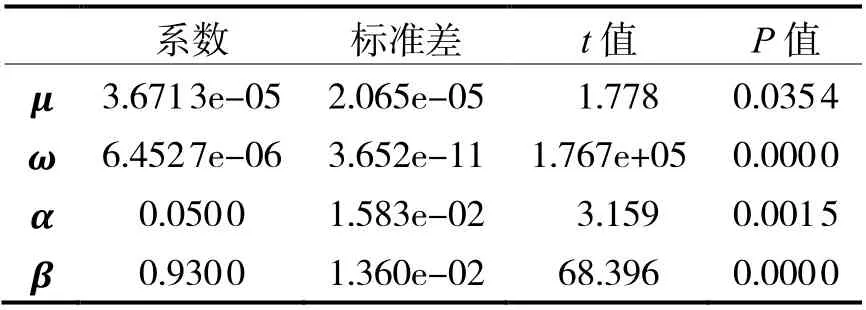
表1 GARCH（1,1）拟合结果

每一个参数估计的P值均小于0.05，因此认为使用GARCH 模型拟合序列的波动性是有效的。对残差做LM 检验，P值显示为0，均表明模型的残差项不存在异方差现象。再次证明本文所建立的GARCH 模型基本满足要求。

对残差序列进行描述性统计分析，偏度与峰度值分别为-0.736 463 与3.204 403，均表明残差序列具有明显的过量峰度和左偏。对其进行偏态检验，进一步判断残差序列是否满足正态分布，得到Q-Q 图如图2 所示。从图2 中可以看出，残差序列的两端都明显偏离了中间的直线，并不服从正态分布。因此，原创业板的收益率序列及其残差序列都不能被认为是服从正态分布的，它们都存在尖峰厚尾现象。

图2 残差序列Q-Q 图

4 尾部估计

极值理论主要研究的是分布中严重偏离均值的数据，侧重于描述序列分布的尾部特征，正好适合用于金融序列的尾部建模和风险度量。曾有多位学者在原有时间序列模型基础上，引入极值理论对主板市场、基金、期货等金融资产进行风险测度研究，效果均比为未引入极值理论要好。而基于创业板市场与主板市场的联合分析可以发现，创业板市场的极端情况发生的频率更高，再次证实引入极值理论对极端情况进行拟合分析的必要性。本文利用极值理论（EVT）对尾部进行估计，使用GPD 分布的POT 方法来对极端事件进行建模。使用R 语言软件中的evir 程序包绘制Hill 图与均值超额函数图，如图3 所示。通过图3(a)中可以看出，在区间(188, 213)之间，图像开始趋于稳定，此时对应的阈值的范围为(0.016 08, 0.017 44)，在此区间内图3(b)也同时呈现平稳的趋势，因此认为在该范围内选择确定阈值是可行的、合理的。本文经过反复验证，最终确定阈值为 ᵆ=0.016 9，此时，超过阈值的样本数为 Nᵆ=195 个，超过样本总数的10%，不会因极值的样本量过少而导致拟合不足，也不会因样本量过多而导致拟合过度。

图3 阈值确定

在R 软件中设置阈值u并建立POT 模型，并对超过阈值的极值数据进行GPD 分布的拟合，得到诊断组合图，如图4 所示。

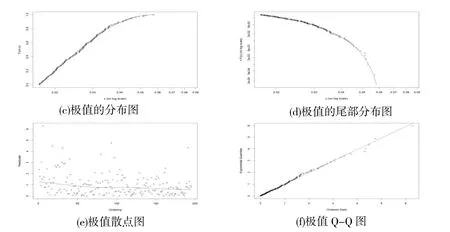
图4 极值部分GPD 分布拟合诊断图

其中，图4(c),(d)分别为极值数据分布图及其尾部分布图，图上的点均落在了实线上或者落在实线附近，这说明模型的拟合效果良好；图4(e)为极值数据的散点图，图中大部分的点都集中在曲线周围，说明GPD分布的拟合效果较好；图4(f)为极值数据的Q-Q 图，图上的点均落在直线及其周围，进一步说明数据服从GPD 分布，拟合效果非常好。

经过检验，已经证明了该模型对序列尾部的极端数据具有不错的拟合效果。利用极大似然估计法，得到参数的估计值为 ᵰ̂=0.460 847，ᵯ ̂=0.007 788；残差序列 ᵄᵆ在q分位数下风险价值和预期损失估计即( VaR(ᵄ)ᵅ和 ES(ᵄ)ᵅ)的计算公式为

将参数估计值代入以上公式，得到的计算结果如表2 所示。

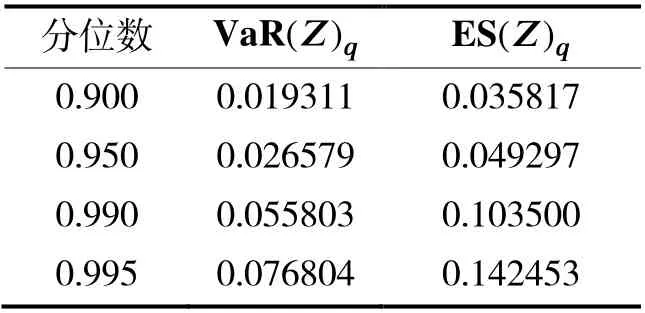
表2 残差序列VaR 与ES 计算结果

5 动态风险度量

将以上两个部分的模型结合，最终能得到在各个分位数下第t期的动态风险价值与预期损失的计算公式，如当分位数q取0.99 时，VaR 与ES 的计算式为

其中，μt+1和 σt+1可由GARCH(1,1)模型计算得到。

6 回测检验与结论

利用GARCH-EVT 模型计算出的VaR 与ES 都仅仅只是估计量，或多或少会存在着一定误差，因此需要检验模型的估计效果，本文选取2019 年10 月8 日至2021 年9 月30 日共486 个交易日的数据作为检验样本，即T 为486。采用失败频率检验方法对模型进行回测检验。为了更加清晰地了解GARCH-EVT 组合模型的效果，本文还另外使用历史模拟法与普通的GARCH 模型进行比较分析，分别在0.900, 0.950, 0.990与0.995 的置信水平下进行返回检验，得到失败天数N与失败频率P如表3 所示。

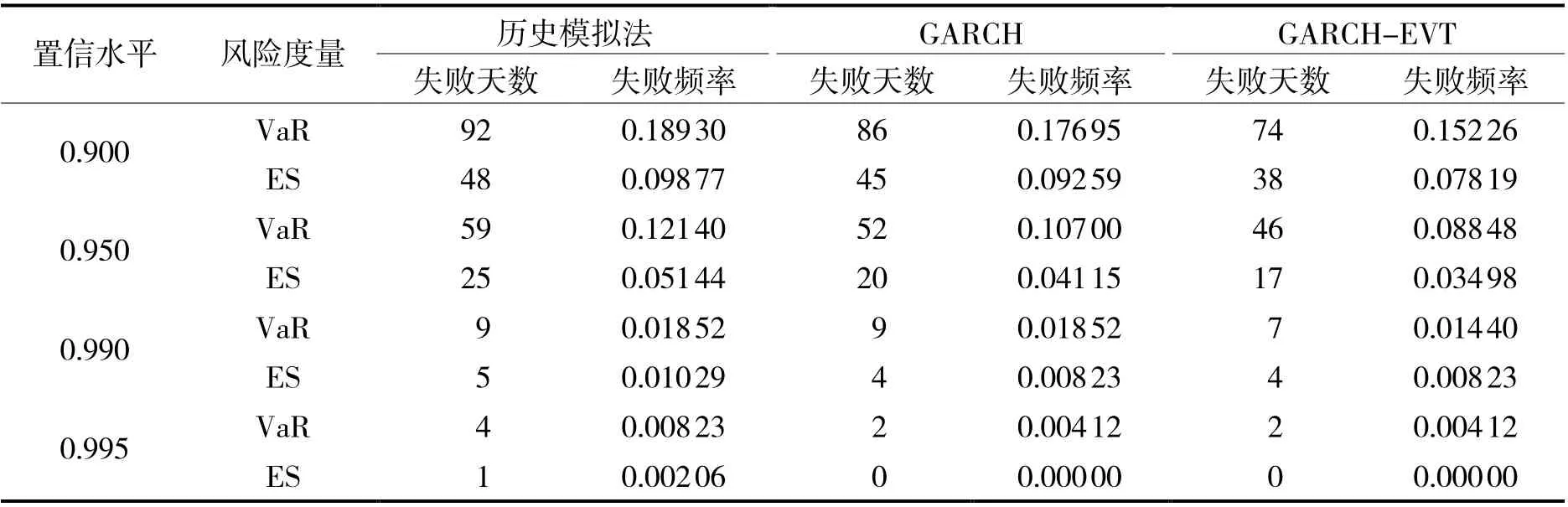
表3 回测检验结果

对表3 中数据从3 个角度进行分析，能够得到以下几点结论：

（1）置信水平的角度。在较高的置信水平下，3 个模型的估计效果都倾向于高估风险；尤其是在0.995的置信水平下，GARCH 模型与GARCH-EVT 组合模型对ES 的估计失败天数为0，成功预测到了再所取的样本时间区间内的风险。但是随着置信水平的降低，失败频率逐渐升高，对VaR 的估计失败频率在数值上普遍超过了置信水平的值，模型的估计效果会有所减弱。

（2）选取模型的角度。在相同置信水平的条件下，GARCH-EVT 组合模型对于VaR 与ES 的估计失败天数，与历史模拟法以及普通GARCH 模型相比都是最少的，说明GARCH-EVT 模型对创业板的动态风险预测较另外两个模型更为准确和有效，更能够预知更多的极端风险。

（3）风险度量指标的角度。比较VaR 与ES 的风险度量效果，从表中的数据能够明显看出，不管采用哪一种模型进行估计，ES 的失败天数都是要少于VaR 的，说明ES 对风险的测度比VaR 的测度更为保守，更适合用来估计和预测极端事件发生，度量极端风险。