我国天然气消耗量的影响因素分析及预测

王珂，张权，郄慧娟

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

随着我国经济的快速发展，能源消耗量也随之攀升，能源安全与环境问题日益突显，天然气作为优质高效的清洁能源在推动低碳循环发展态势下得到极大推广，有效地改善了环境质量，由此其消耗量快速增长，与天然气产量的增速差距不断加大，因此正确分析天然气消耗量的影响因素及其影响程度并对天然气消耗量进行合理预测研究，对我国天然气的生产管理和调度优化，实现节能减排、安全平稳供气，保障国内天然气稳定供应具有重要意义。

众多学者对天然气消耗量的影响因素及预测进行了研究，付佳鑫[1]利用模型分析影响北京天然气消费的主导因素机理，认为GDP、能源消耗强度、能源消费结构以及能源低碳化进程，是影响北京天然气消费的主要因素。宗庆莹[2]采用灰色模型对我国天然气消费量的增长趋势加以预测，并采用灰色关联度分析法对可能会影响天然气消费总量的条件进行分析，认为天然气消费总量将持续增长，且增速有所加快，天然气产量和居民消费水平与天然气消费量的关联度最大。闵晶晶[3]等采用经验模态分解、相关分析等方法分析北京地区采暖季天然气消耗量的年际变化特征及影响要素，利用BP 神经网络方法构建采暖季天然气消耗量预测模型，认为天然气消耗量呈现持续增加趋势，EMDBP 预测模型具有较好的预测效果。

综上研究，学者已经对天然气消耗量影响因素及预测的各方面和各种方法进行了探究。本文在学者们研究的基础上加入近些年天然气消耗量相关数据，选取更多指标，对天然气消耗量影响因素进行更为全面的探究。通过运用灰色关联度分析法探究近年来我国天然气消耗量的影响因素及各因素影响程度，在此基础上运用GM(1,1)和GM(1,N)建立天然气消耗量预测模型，对天然气消耗量进行合理预测[4]，旨在为我国天然气产量结构调整，天然气资源的生产、进出口安排，以及能源战略的制定提供参考。

1 数据来源与变量选取

1.1 数据来源

本文的数据来源于RESSET 数据库和国家统计局官网及《中国统计年鉴2021》。

1.2 变量选取

通过对已有文献的阅读整理以及当今国家社会的发展状况，可知国家经济的蓬勃发展离不开自然资源的禀赋，而天然气是自然资源的重要组成部分，作为可利用的重要自然资源，天然气在经济的发展中具有突出贡献，因此影响天然气的消耗量的因素与社会经济、科学技术、基础设施等各个方面具有重要联系[5]。从而选取人口数、GDP、居民消费水平、第一产业占比、天然气生产量等23个指标。如表1。

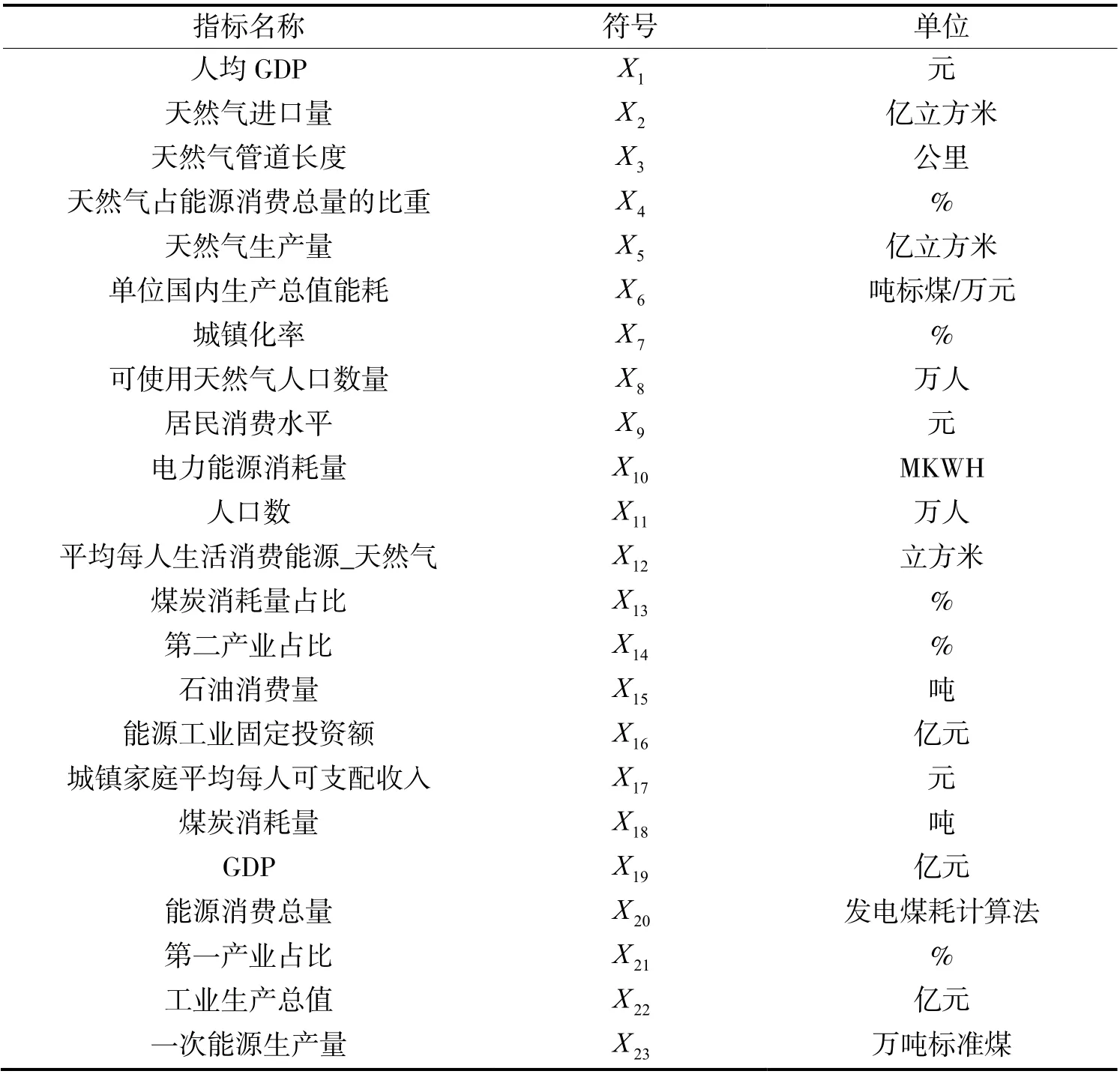
表1 指标名称、符号及单位

2 天然气消耗量影响因素分析

2.1 灰色关联分析理论模型

灰色关联度分析可以在众多的因素中，根据序列曲线几何形状的相似程度判断其各因素联系是否紧密，曲线越接近，相应序列之间关联度就越大，反之就越小[6]。基本步骤如下：

第一步，确定特征序列和相关序列设特征序列为Yj= {Yj(k) |k= 1,2,3, …,n}，j= 1,2,3, … ,n，相关序列为Xi={X i(k) |k= 1,2,3, …,n}，i= 1,2,3, … ,m。

第二步，针对数据进行无量纲化处理。不同序列的量纲不同，可以采用初值化、均值化、平移化等方法进行处理。本文采用均值化处理，公式如下：

第三步，求解母序列（对比序列）和特征序列之间的灰色关联系数值。根据均值法的结果，求出母序列与每个相关序列之间的绝对差，记为 ΔXji=，根据求出的绝对差 max =和min =，代入公式中计算出关联系数。

2.2 实证分析

选取1994～2021 年相关指标数据，使用SPSS 软件进行天然气消耗量的影响因素分析。

选取天然气的消费量作为母序列，其他影响天然气的消耗量的因素作为特征序列，进行归一化处理，并根据计算公式计算关联度系数，如表2。

表2 灰色关联系数

在分辨系数取0.5 的前提下，由表2 可知大多数变量与天然气消费量的关联度系数大于0.5，少数变量在个别年份的关联度系数小于0.5，可见本文选取的变量与天然气的消耗量关联性较强。

根据求得的灰色关联度值，将其排序，得到关联度结果如表3 所示。

由表3 给出的关联度程度排序，可知，与天然气消费量关联程度最强的是经济水平因素中的GDP，最弱的是产业结构因素中的第一生产占比，相比较GDP，其次是使用天然气人口数量和人均GDP。

表3 灰色关联度结果

3 基于模型的天然气消耗量预测分析

3.1 灰色预测模型

灰色理论将无规律的历史数据经过累加以后，使其成为具有指数增长规律的上升形状数列，由于一阶微分方程解的形式是指数增长形式，所以可以对生成数列建立微分方程模型。即灰色模型实际上是对生成数列建模[7]。灰色模型可以解决历史数据少、序列的完整性以及可靠性低的问题，能将无规律的原始数据进行生成得到规律较强的生成序列。但是只适用于中短期且近似于指数增长的预测。

GM(1,1)针对线性数据具有较好的预测效果，并且在预测时只考虑了自变量本身的影响，而没有考虑其他外界影响因素对预测结果的影响作用，因此有了多维灰色预测模型GM(1,N) ，其中N表示考虑的相关因素维度，其预测原理与GM(1,1)的不同之处在于输入数据变量是N个。模型如下：

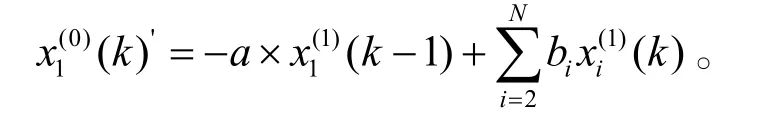
3.1.1 建模过程

设系统有特征数据系列：

相关因素序列：

生成的紧邻均值数列：

根据灰色理论对建立微分方程GM(1,N) ：

其中，a称为发展系数，bi称为驱动系数，bi xi(1)(k)称为驱动项。

引入向量矩阵记号：

采用最小二乘法可求得u：

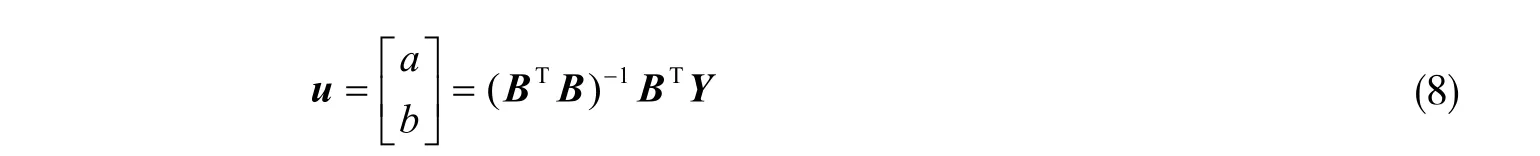
当i= 1,2, …,N变化幅度较小时，模型的近似时间响应式：

累减还原式：

差分模拟式为

3.1.2 模型检验

根据上面得到的预测值xˆ(0)(i)，计算原始序列x(0)(i)与xˆ(0)(i)的绝对误差序列以及相对误差序列。残差序列：

相对误差：

3.2 预测模型的构建与预测结果分析

通过建立背景值优化的GM(1,1)模型和GM(1,N) 模型预测后两年的天然气消耗量，用精度、平均相对误差作为评价模型准确程度的指标。

3.2.1 GM(1,1)预测

用MATLAB 做GM(1,1)预测，为了保证GM(1,1)模型的可行性，需要对已知的数据进行级比检验。

通过级比检验，可知可容覆盖区间为λk= ( 0.9286,1.0769)，原数据未通过检验，因此，做平移变换可得，C= 318706 431时，数列的级比都能落在可容覆盖区间内，可进行GM(1,1)的建模和预测[8]。

对Y(0)累积相加，生成AGO 序列，用改进的背景值代替紧邻均值构造的背景值序列，用最小二乘法可得a和b的值为

GM(1,1)的预测公式为

1994～2021 年中国实际的石油消耗量与背景值优化的灰色模型预测石油消耗量的变化如图1。

图1 GM(1,1)模型预测天然气消耗量与实际消耗量变化

3.2.2 GM(1,1)预测

由于天然气消耗量的多少受多方面因素的影响，简单的GM(1,1)模型并不能反映各个因素的作用，为了使模型预测地更精确，需要将GDP、天然气的消耗量、平均每人生活消费的天然气等因素考虑在内，从而优化模型。

根据灰色关联度分析的结果，可将影响天然气消耗量的影响因素按重要程度排序，用python 进行GM(1,N) 的多次模拟，最终选择模拟效果最好，关联度最高的4 个影响因素，即：国民生产总值GDP、可使用天然气人口数量NGU、人均GDP、居民消费水平HCL，建立GM(1,4)模型。根据上述的理论分析，只要确定参数的值，就可以求出每年的天然气的消耗量。

设a天然气的消耗量为特征序列，相关因素序列分别为国民生产总值GDP、可使用天然气人口数量、人均GDP、居民消费水平，用python 计算可求出相关参数的值。发展系数：

驱动系数为

GM(1,4)的近似时间响应式为

平均相对误差：

模型精度：

上述两个模型的对比发现，GM(1,4)的模型精度远远高于GM(1,1)，因此GM(1,4)的预测效果较好，根据GM(1,4)的预测模型，可求得2020 年和2021 年的天然气消耗量分别为为42 368 692 m3和44 381 824 m3，预测结果比较准确，根据模型公式可计算2022 年天然气的消耗量为46 338 292 m3。

4 结束语

基于我国1994～2021年天然气消耗量相关数据，采用灰色关联分析法分析可能影响天然气消耗量的23个指标与天然气消耗量的关联程度，用两种不同的灰色模型预测天然气消耗量（图2）。结果表明：国民生产总值GDP和可使用天然气人口数量与天然气消耗量的关联程度最大，GM(1,4)模型的预测精度更高，2022年天然气的消耗量将达到46 338 292 m3。

图2 GM(1,4)模型预测天然气消耗量与实际消耗量变化

适度加大天然气勘探开发力度。由于天然气管道建设不够完善，我国天然气能源的开采较其他国家较低，应完善天然气管道等相关设施，适度加大天然气的开采，维持天然气消费的供需平衡。

加大对天然气的科研力度，降低勘探成本。在增加开采规模的基础上还要不断增加新勘探技术研发投入，提高天然气的利用率，有效降低勘探和开采成本。

优化产业和能源结构。适当降低第一、第二产业比重，积极向第三产业倾斜[9]，同时降低煤炭等高污染物排放能源的消耗，提高清洁能源天然气的利用率。