核心素养视角下的数学概念教学*
——以“等差数列的概念”教学设计为例
唐芝彬 吴莉娜
(1.江苏省常州市戚墅堰高级中学,213299;2.江苏省常州高级中学,213004)
“等差数列的概念”是苏教版选择性必修一第四章第二节第一课时的内容.本章第一节已经介绍了数列的基础知识,而等差数列是数列中一种十分重要的数学模型.要求学生:用数学语言去描述数列,从而构建等差数列的概念;观察数列,进行归纳推导等差数列的通项公式;证明等差数列的通项公式;根据实际应用情境,构建等差数列的模型,从而解决实际问题.本文以此教学设计为例,对数学概念教学进行探究.
一、教学过程
1.创设情境,激发兴趣
师:如图1,这是2021年11月份的日历.你能说出周一分别是哪几号吗?
生:1,8,15,22,29.
师:这组数构成数列吗?判断的依据是什么?
生:这组数构成数列.按照次序排列的一列数.
师:再看图2,这个电影院设置了20排座位,已知第一排座位数为38个,从第二排起,后一排比前一排多2个座位,你能说出这个剧场各排的座位数分别是多少吗?
生:38,40,42,44,46…
师:这组数构成数列吗?判断的依据是什么?
生:这组数构成数列.按照次序排列的一列数.
师:我国在2022年举办了冬奥会,已知2022年是第24届冬奥会,并且冬奥会是每隔4年举办一次.你能说出在2022年之前哪些年份举办了冬奥会吗?
生:2 018,2 014,2 010,2 006…
师:这组数构成数列吗?判断的依据是什么?
生:这组数构成数列.按照次序排列的一列数.
设计意图以日历、电影院、冬奥会这三个生活中的实例作为情境,让学生观察并建构数学模型,增强学生的学习兴趣,发展学生的数学抽象、数学建模与直观想象的素养.
2.归纳猜想,生成概念
例1大家一起来观察我们刚写出的三组数列,① 1,8,15,22,29;② 38,40,42,44,46…;③ 2 022,2 018,2 014,2 010…你能发现这三组数列各自有什么特点?这三组数列又有什么共同特征呢?
生1:我发现第一组数列每两个相邻的数之差为7,第二组数列每两个相邻的数之差为2,第三组数列每两个相邻的数之差为-4.
生2:我发现这三组数列中,后一项减前一项都是一个固定的常数.
师:那老师问大家一个问题,第一项呢?
生:从第二项起,后一项减前一项都是一个固定的常数.
师:由此可以得到等差数列的概念.一般地,如果一个数列从第2项起,每一项与前一项的差都等于同一个常数,就称这个数列为等差数列,这个常数就称为等差数列的公差,用d来表示.能否用数学符号语言表示?
生:an-an-1=d,n∈N*.
师:大家来看一下,这一表述有没有问题?
生:n=1时怎么办?所以要添加条件.
师:数学符号语言可写为an-an-1=d,n∈N*,n≥2.
设计意图以教师为主导、学生为主体的原则,理解等差数列的概念及通项公式的推导过程,培养学生归纳总结能力,发展学生数学抽象的素养.
3.学习探究,辨析概念
例2判断下列数列是否为等差数列,如果是,请你说出首项和公差;如果不是,请说明理由.
① 1,3,5,7;
② 9,6,3,0,-3…;
③-8,-6,-4,-2,0…;
④ 3,3,3,3…;
⑤ 15,12,10,8,6…;
⑥-3,-6,-9,-12,-15….
(回答过程略)
师:同学们是怎么判断这些数列是否为等差数列的?
生:根据等差数列的概念,看数列中所有后一项减去前一项是否为同一个常数,如果是,就是等差数列;如果不是,就不是等差数列.
设计意图通过具体的例子,其中包含了公差为正、负、0与不是等差数列的各种情况,让学生判断,增强学生对于等差数列概念的理解.
4.类比推理,拓展概念
例3证明:已知数列的通项公式为an=pn+q,其中p,q为常数,那么这个数列是等差数列吗?
生:当n≥2时,an-an-1=pn+q-p(n-1)-q=p,因为p为常数,a1=p+q,故是以首项为p+q,公差为p的等差数列.
例4观察如下的两个数,插入一个什么数后,三个数就会成为一个等差数列.
① 2,______,4;
②-1,______,5;
③-12,______,0;
④ 0,______,0.
生:可以设插入的数为x,既然这组数列是等差数列,一定会有x-2=4-x,所以2x=4+2,即x=3.其他数列以此类推.
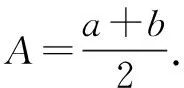
再来回顾引例中的三组数列,① 1,8,15,22,29;② 38,40,42,44,46…;③ 2 022,2 018,2 014,2 010….可以发现,从第二项起,每一项都是它的前一项和它的后一项的等差中项.对于这三组数列是否存在通项公式呢?如果存在,请写出通项公式?
临床既往的教学模式为传统带教方法,学生所学的知识均为被动接受,学习目标也不是十分明确,难以达到理想的教学效果,学生的需求也难以满足[11-12]。特别是对于医学留学生,由于思维差异大及语言沟通难度大,传统的临床教学方法难以满足日益增多的留学生教学的要求[13-14]。近年来,在临床教学模式中,PBL教学法应运而生。PBL教学法起源于20世纪50年代的医学教育,目前已成为国际医学教育通用的教学方法之一[15-16]。
生:①an=7n-6;②an=2n+26;③an=-4n+2 026.
师:对于一些具体的数列,大家可以写出通项公式,那对于一般情况下,给你a1和d,你能不能写出a2,a3,a4呢?
生:a2=a1+d,a3=a2+d=a1+2d,a4=a3+d=a1+3d.
师:能否给出an呢?
生:由等差数列的定义,可以归纳得出an=a1+(n-1)d.
师:这种方法我们称为归纳法.还有没有其他方法呢?由a2-a1=d,a3-a2=d,a4-a3=d,…,an-an-1=d,共有n-1个d,所以左右两边分别相加,可以得到an-a1=(n-1)d,故an=a1+(n-1)d,称这种方法叫做累加法.由此给出等差数列的通项公式,an=a1+(n-1)d.已知一组等差数列的首项和公差(两个基本量),就可以确定任意一项;公式中共有an,a1,n,d四个量,已知其中三个可求另一个.
设计意图通过习题让学生自己归纳总结出等差中项的定义,结合情境中的三个数列让学生自主探究得出等差数列的通项公式,并给出两种方法推导出等差数列的通项公式,培养学生归纳总结的推理能力,发展学生的逻辑推理、数学运算素养.
5.问题引导,知识应用
生:设等差数列的通项公式为an=a1+(n-1)d,a1=8,d=a2-a1=5-8=-3,所以an=8+(n-1)×(-3)=11-3n,故a20=11-3×20=-49.
例6-401是不是等差数列-5,-9,-13,…的项?如果是,是第几项?
生:∵a1=-5,a2=-9,∴d=a2-a1=-9-(-5)=-4,∴an=a1+(n-1)×d=-5+(n-1)×(-4)=-4n-1,由-4n-1=-401,n=100.故-401是这组数列的第100项.
例7《莱因德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和是较小的两份之和的三倍,则最小的一份是多少?
生:设五个人分得得面包分别为a-2d,a-d,a,a+d,a+2d(其中d>0),则有(a-2d)+(a-d)+a+(a+d)+(a+2d)=100,∴a=20,由a+(a+d)+(a+2d)=3[(a-2d)+(a-d)]得,3a+3d=3(2a-3d),∴12d=3a,故d=5.则最小的一份为a-2d=20-10=10.
设计意图应用等差数列的定义、通项公式及等差中项的定义解决实际问题,发展学生的数学运算素养.
6.知识归纳,课堂小结
师:本节课你学到了那些知识?
生:学习了等差数列与等差中项的概念,等差数列的通项公式,运用通项公式和递推关系去研究数列.
师:本节课运用了哪些思想方法?
生:枚举法,归纳法,累加法,从特殊到一般,基本量法.
二、教学启示
1.重视概念生成,培养学生建模能力
首先从日历中的周一日期、电影院的座位数和冬奥会的举办年份三个生活中的情境出发,从实际生活问题抽象概括出数列模型,让学生观察三个数列模型的共性,提炼出等差数列的定义、数学表达式及特点,抽象出等差数列的概念,使学生体会在现实生活中可以汲取到解决数学问题的智慧,让学生对本课后续内容的学习产生期待,培养学生数学建模的能力.
2.重视问题引导,促进学生思维发展
基于问题引导的探究式学习应当以“导入——自学——精讲点拨——课堂训练——总结”为主要教学环节.本文以提出问题、分析问题、解决问题为线索贯穿整个教学环节.问题引导应当基于实际教学内容,以合理巧妙设计问题串的形式帮助学生对知识的理解与掌握.
3.重视过程渗透,提升学生数学素养
首先从实际生活情境观察提炼数学模型,让学生了解等差数列概念的形成过程,从而得出等差数列的概念,发展学生数学抽象、数学建模与直观想象的核心素养.其次通过自主辨析判断数列是否为等差数列,类比递推得出等差中项的概念与等差数列的证明,发展学生逻辑推理与数学运算的核心素养.再次通过解决等差数列求通项的例题与数学著作中的生活实际问题深化对等差数列的理解,发展学生数学建模与数学运算的核心素养.最后总结数学方法的运用.整个教学环节应深入挖掘等差数列的知识所承载的数学核心素养,落实培养学生数学核心素养的目标.
基于核心素养的数学概念教学,应当坚持以学生为主体、教师为主导的原则,将课堂真正还给学生,给予充分的时间让学生进行自主探究与合作学习.这就需要精心设计教学环节,让学生经历通过生活实例建构数学模型的过程,从而理解数学概念的本质特征,充分激发学生学习兴趣,发展学生数学抽象、数学建模、逻辑推理、直观想象与数学运算的核心素养.

