电机材料对永磁同步电机噪声影响的分析*

王枫麒，于慎波，夏鹏澎，窦汝桐，宅凤晨

（沈阳工业大学机械工程学院，沈阳 110870）

0 引言

不同电机材料的性能差别很大，常见的材料性能有弹性模量、密度、泊松比等，针对电机材料，不同材料的饱和磁感应强度也是不同的，这些材料参数会影响电机的运行性能。振动噪声作为电机的重要性能之一，始终受到大量专家学者关注。韩汇文[1]对永磁同步电机的电磁场和振动特性进行了耦合分析；赵森磊[2]对不同加工工艺的永磁同步电机振动噪声进行了测试分析；OKAMOTO S等[3]对永磁同步电机不同材料铁损进行研究；ZHU Z Q等[4]对表贴式永磁同步电机空载磁场进行了解析计算，并验证了准确性。但是有关永磁同步电机材料性能对噪声影响的研究相对较少。本文以某公司大批量生产的功率为9 kW、8极36槽的小型永磁同步电机为研究对象，该电机广泛应用于于半导体制造设备、贴片机、印刷电路板打孔机、搬运机械、食品加工机械、机床、传送机械等自动化设备，对振动噪声的控制有一定要求。

本文首先对电机不同定子铁心材料的圆周方向的模态频率进行了解析计算，然后利用ANSYS Maxwell与Workbench有限元软件分析，最后通过电磁-机械耦合的方法，计算定子铁心齿部及机壳表面振动速度，得出永磁同步电机周围的噪声等级，分析不同定子铁心材料以及不同永磁体的材料性能对小型电机振动噪声的影响。

1 电机定子材料的模态分析

目前用于电动机结构固有模态计算的常用解析法为机电阻抗理论和圆柱壳理论，常用能量法为傅里叶级数法和有限元法，本文主要采用的解析法为圆柱壳理论，能量法为有限元法。

对于一个薄壁圆筒，m阶周向固有频率可以表示为：

式中：fm为薄壁圆筒m阶周向固有频率，Hz；Km为薄壁圆筒m阶周向固有模态的等效刚度，N/m；Mm为薄壁圆筒m阶周向固有模态的等效质量，kg。

当薄壁圆筒的长径比l/D≤1时，可以采用Hoppe理论计算，其薄壁圆筒的m阶周向频率为[2]：

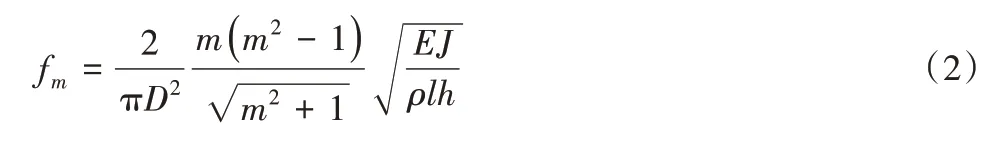
式中：D为薄壁圆筒平均直径，m；l为薄壁圆筒有效长度，m；h为薄壁圆筒壁厚，m；ρ为薄壁圆筒密度，kg/m3；E为薄壁圆筒弹性模量，N/m2；J为平行于薄壁圆筒轴线的截面对其轴线的惯性矩。

当圆筒外壳的直径厚度比大于90时，用Hoppe理论公式计算圆周方向的固有频率。如果圆筒形壳体的直径厚度比小于90，则在式（2）上加上圆筒形壳体直径厚度比的系数，得到改进的圆筒形壳体周向的固有频率计算公式。当周向模态阶数m=2时，圆周固有频率的计算公式为式（2）。圆周方向固有频率大于或等于3时，圆周方向固有频率的计算公式为：

式中：f2为m=2时圆柱壳体的周向固有频率；Fm为m≥3时的各阶模态修正系数。

式中：Δ为径厚比影响系数；εi为模态阶数影响系数。

当圆柱壳体径厚比小于30时，通过对不同径厚比圆柱壳体的Hoppe理论与有限元的周向固有频率变化率运用最小二乘法多项式拟合得径厚比影响系数为：

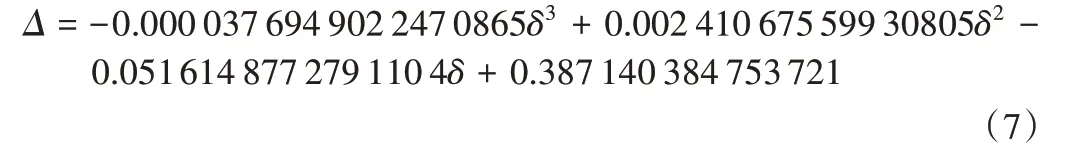
式中：δ为径厚比。

使用改良后圆柱壳体周向固有频率计算公式计算定子铁心的周向固有频率。将定子铁心简化成与原模型的外径、体积且长度相同的圆柱壳体（如图1所示），由于简化的原因，会造成简化的模型与原模型的刚度产生误差，因此对式（1）和式（4）添加模型简化刚度修正系数Cm，则新的计算定子铁心周向固有频率的解析公式如下。

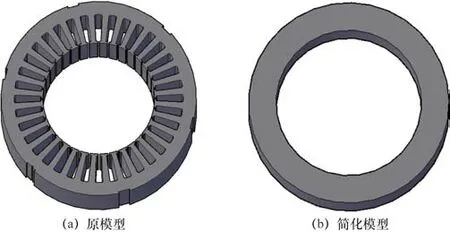
图1 定子铁心的结构模型

当m=2时：

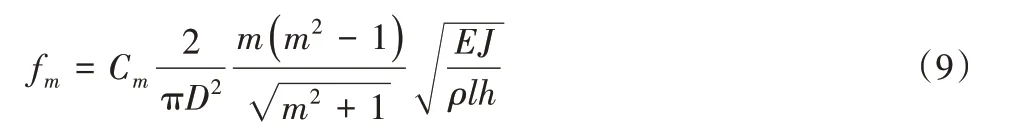
当m≥3时：

式中：C2为m=2是简化定子铁心模型造成的刚度修正系数；Cm为刚度修正系数。

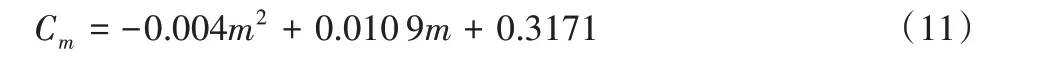
利用式（9）和式（10）对等效的圆柱壳体的周向固有频率进行解析法计算，且利用有限元法对不同材料定子铁心的周向固有频率进行数值计算，其计算结果对比如表所示。分别使用硅钢材料以及非晶合金材料作为永磁同步电机的定子铁心。电机的定子的主要材料参数如表1所示。

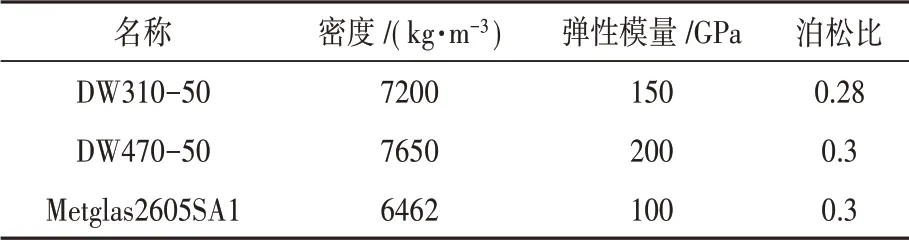
表1 电机定子主要材料参数

求解定子铁心的前20阶模态，定子铁心振动的前6阶振型如图2所示。但定子的模态振型只是表征形状的变化趋势，并不代表真实的形变量，用不同颜色代表不同的形变程度，图中颜色越趋于红色代表形变趋势越明显。相邻两模态阶数之间的频率相对变化量为159.53%、71.99%、39.30%、17.11%。本文研究的永磁电机工作频率为200 Hz，最高转速为1 500 r/min，所以在电机正常运转情况下，不会发生共振现象。

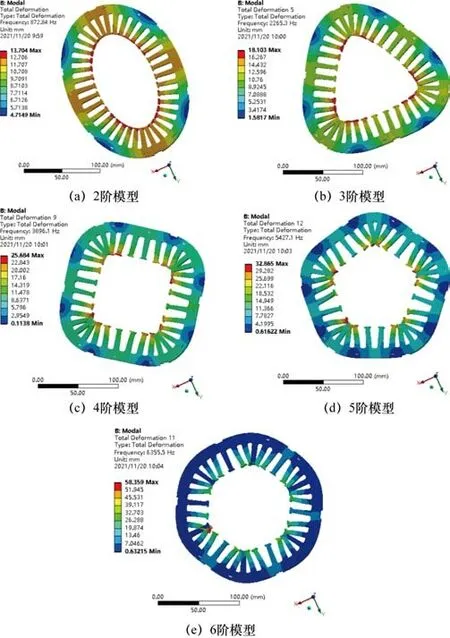
图2 定子前6阶振型

利用式（9）和式（10）对等效的圆柱壳体的周向固有频率进行解析法计算，且利用有限元法对不同材料定子铁心的周向固有频率进行数值计算，其计算结果对比如表2所示。由表可知，定子铁心周向固有频率的改良后解析公式结果与有限元结果误差在2.8%以内，可以验证解析式的准确性，为不同材料的模态频率预测提供了参考。

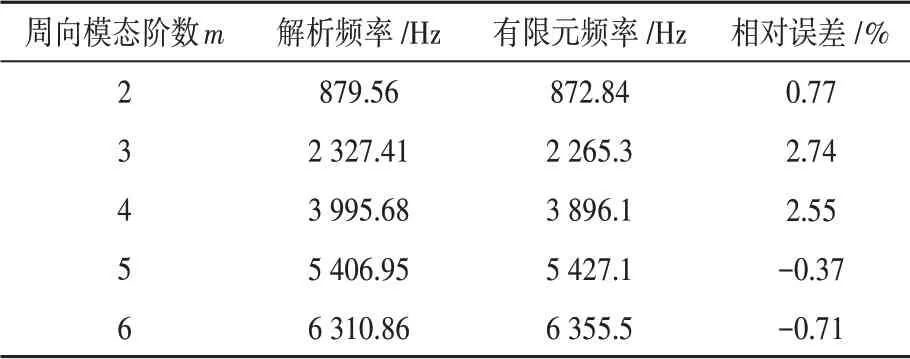
表2 解析法与有限元计算的定子铁心周向固有频率的对比

图3所示为不同定子材料解析模态频率值曲线。由图可以看出DW470定子铁心的各阶固有频率要大于DW310定子铁心各阶固有频率，DW310定子铁心的各阶固有频率要大于Metglas2605SA1定子铁心各阶固有频率，由式（9）可以看出，定子铁心的固有频率受材料的弹性模量与密度的影响，由于弹性模量变化的影响大于密度变化的影响，所以电机同一阶的固有模态频率也随之增加。因此可以通过改变定子铁心材料的材料属性来改变电机的固有频率，从而防止共振，进而降低噪声。

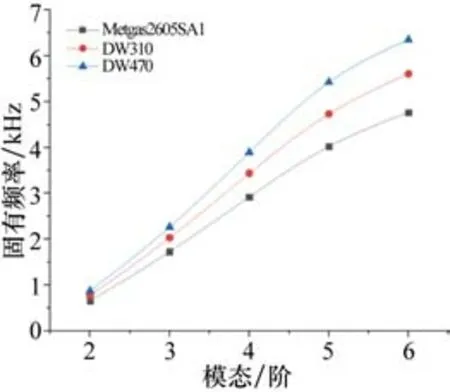
图3 不同定子材料解析模态频率

2 电磁振动分析的有限元设计

为了更好地了解转子永磁体产生磁场的情况，可以观察电机磁力线及磁通密度的分布情况。稳定运行之后，电机的磁感应强度分布如图4所示。由图可以清楚地看到永磁同步电机8个极的位置，以及磁场分布情况。由于铁心、轴和空气的磁导率不同，所以磁力线分布疏密不同。磁通密度在定子齿顶部和永磁体之间较大，在定子槽和永磁体之间较小。

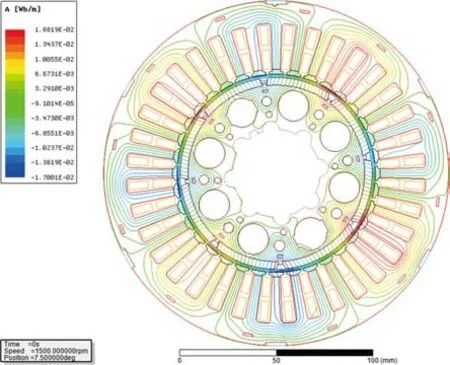
图4 永磁同步电机磁感应强度分布

定子齿某一点径向及切向电磁力及谐波分析如图5～6所示。可以看出径向电磁力密度的高次谐波幅值很小，影响很小，可以忽略不计，主要起作用的是低次谐波。

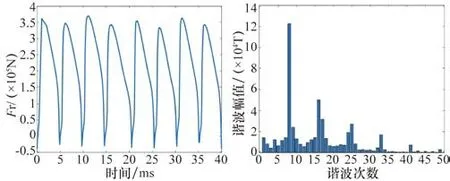
图5 定子齿某一径向点电磁力及谐波分析

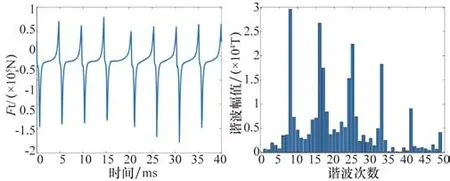
图6 定子齿某一点切向电磁力及谐波分析

电机定子不同材料的平均转矩与转矩脉动如图7～8所示。由图可以得到结论：（1）不同铁心材料的转矩是不同的，DW470的平均转矩要高于DW310，DW310的转矩要高于非晶合金Metglas2605SA1；（2）不同铁心材料的转矩脉动也是不同的，DW470的转矩脉动要稍高于DW310，非晶合金Metglas2605SA1的转矩脉动要明显高于DW310与DW470，DW310与DW470的转矩脉动相差不大，非晶合金Metglas2605SA1的转矩脉动要明显大与硅钢电机，意味着电机运行平稳性不如硅钢电机，不利于降低电机振动噪声。

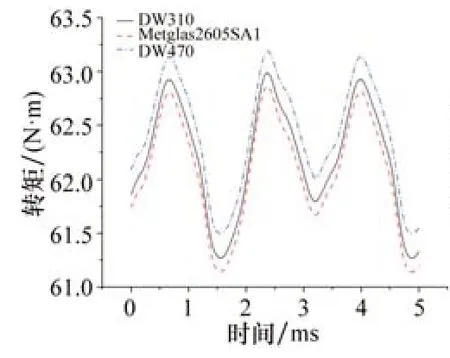
图7 不同定子铁心材料转矩

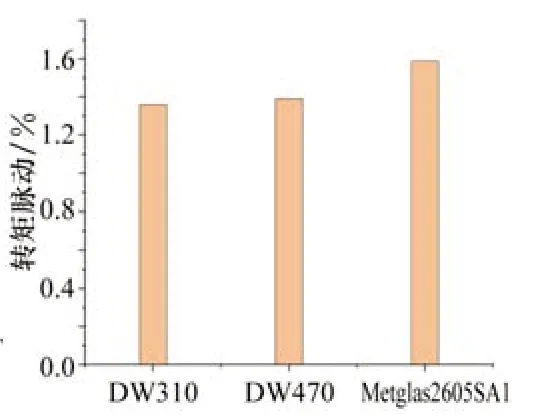
图8 不同定子铁心材料转矩脉动

3 永磁体材料性能对电机性能的影响

磁极材料作为永磁电机关键部件之一对电机磁场有关键作用，直接影响电机气隙磁场，钕铁硼永磁材料具有优异的性能，广泛应用于永磁同步电机中。本文以N33UH、N35UH、N38UH三种钕铁硼永磁材料为研究对象，对三种磁极材料进行气隙磁密分析，研究不同永磁材料对电机振动噪声的影响。永磁体材料的主要材料性能如表3所示。

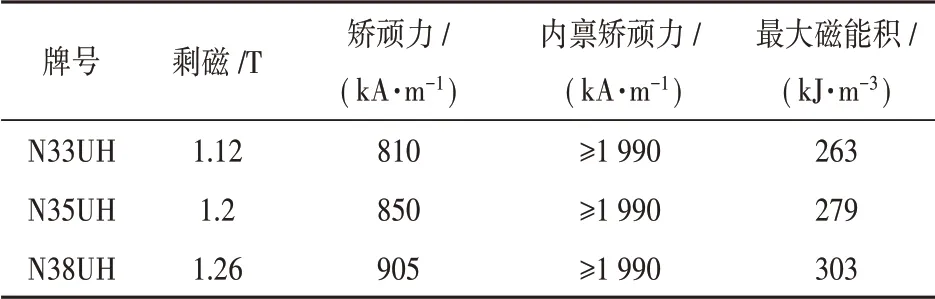
表3 钕铁硼永磁材料的主要材料性能

选取一对磁极不同位置，得到不同永磁体材料的径向磁密曲线如图9所示，可以看出，不同磁极材料的气隙磁密的幅值是不同的，N38UH磁极材料的径向磁密最大，N35UH磁极材料的气隙磁密位于N38UH磁极材料与N33UH磁极材料之间，N33UH磁极材料的径向磁密最小，永磁同步电机定、转子之间气隙内的径向磁通密度和径向电磁力均是随着永磁体剩磁的减小而逐渐减小的，其波形也愈加平缓，峰值的幅值也呈现出逐渐减小的趋势。

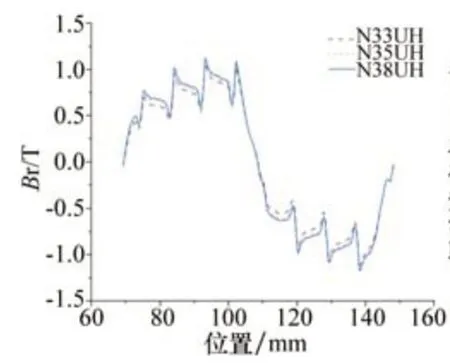
图9 不同磁极材料的径向气隙磁密

4 电机的振动噪声分析

4.1 不同定子铁心材料对电机振动噪声的影响

根据不同材料计算电机定子铁心的振动速度，选择电机定子齿部表面各节点的平均值分析频谱，选择频率分析范围为0～5 000 Hz，如图10所示。由图可知，定子铁心弹性模量为100 GPa电机的振动速度大于定子铁心弹性模量为150 GPa电机，且大于定子弹性模量为200 GPa电机；在2 000 Hz、3 300 Hz、4 600 Hz三个频率点附近有较大的分量。

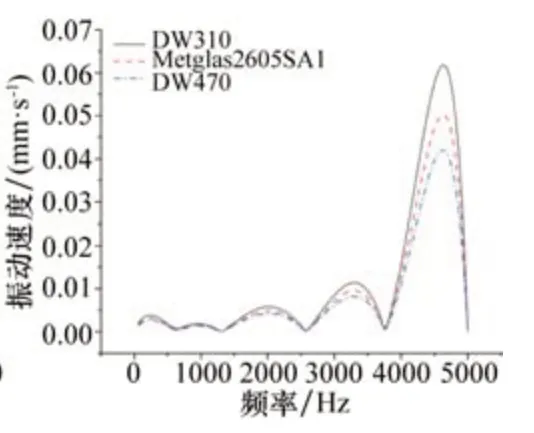
图10 电机定子齿部振动速度频谱曲线

在电机周围1.0 m的区域内，选择某一点，得到电机电磁噪声声压频谱如图11所示。由图可知，在1 500 r/min时，电机噪声幅值有随频率增加而增大的趋势；不同弹性模量定子铁心的声压级差异较大，弹性模量为100 GPa的定子铁心的声压级明显高于弹性模量为150 GPa及200 GPa的定子铁心。声压级与定子铁心弹性模量近似成反比关系，其中弹性模量为100 GPa的定子铁心比弹性模量为150 GPa的定子铁心噪声最大值高约3 dB，弹性模量为150 GPa的定子铁心比弹性模量为200 GPa的定子铁心噪声最大值高约2 dB。

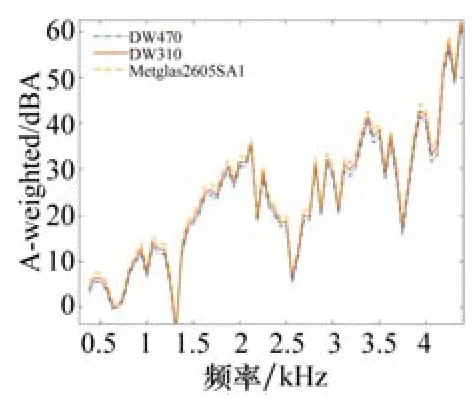
图11 不同定子铁心电机噪声频谱分析

4.2 不同永磁体材料对电机振动噪声的影响

保持定子铁心材料、机壳材料属性不变，通过改变永磁体材料来研究不同永磁体材料对电机振动噪声的影响，定子铁心材料选用DW470硅钢，机壳采用铝合金机壳，在ANSYS workbench中进行谐响应分析，利用MATLAB软件进行后处理。

图12所示为不同磁极材料电机机壳表面振动速度对比曲线，由图可知不同磁极材料机壳处振动速度是不同的，整体振动速度趋势是一致的，N38UH磁极材料在不同频率下的振动速度要大于N35UH磁极材料，N35UH磁极材料在不同频率下的振动速度要大于N33UH磁极材料，在7 003.5 Hz、7 504 Hz、7 837 Hz、8 838 Hz、12 173 Hz、13 010 Hz存在较大分量，其中在12 173 Hz是最大峰值点，N33UH磁极材料机壳表面的振动速度为0.151 4 mm/s，N35UH磁极材料机壳表面的振动速度为0.167 7 mm/s，N38UH磁极材料机壳表面的振动速度为0.185 mm/s。

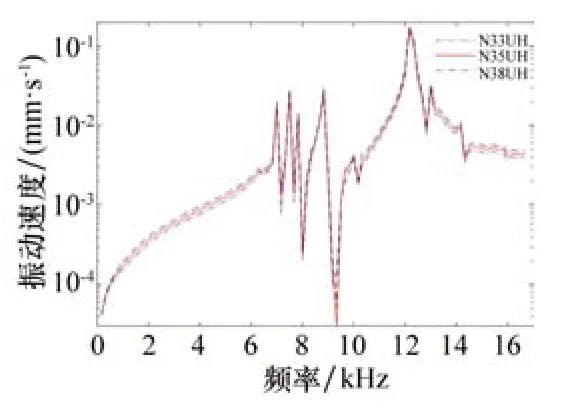
图12 不同磁极材料电机机壳的振动速度响应

选取峰值点12 173 Hz作为研究对象分析不同磁极材料电机的电磁振动噪声的声压级。如图13所示，由图可知，电机机壳表面附近处的声压级有较大值，随着距离机壳越来越远，声压级越来越小，符合客观规律，其中N33UH磁极的噪声最大 值 为94.96 dB，N35UH磁 极 的 噪 声 最 大 值 为96.7 dB，N38UH磁极的噪声最大值为99.87 dB。由此可见，磁极材料对电机噪声有较大影响，在满足电机运行性能的前提下，合理选择电机磁极材料，有利于降低电机振动噪声。

图13 不同磁极材料电机SPL云图

5 结束语

（1）当径厚比较小时，提出了改良解析公式计算定子铁心模态固有频率，并验证了解析方法的准确性。经过电磁场和机械场的耦合分析，得到定子齿部表面的Fr和Ft，结果表明径向电磁力的低次力波是产生电磁噪声的主要原因。

（2）以该小型电机模型为例，声场的分析计算表明：电机的材料性能对振动噪声具有较大影响。弹性模量为100 GPa的定子铁心比弹性模量为150 GPa的定子铁心噪声最大值高约3 dB，弹性模量为150 GPa的定子铁心比弹性模量为200 GPa的定子铁心噪声最大值高约2 dB。在相同频率下，不同永磁体材料电机振动噪声最大值与最小值相差约5 dB。