大型海上风机单叶片高空对接过程的力学分析*

蔡舒鹏，张永康※，金 晔，梁岩峰，姜季江，薛 驰，林 峰

（1.广东工业大学机电工程学院，广州 510006；2.中铁建港航局集团有限公司，广东珠海 519075；3.启东中远海运海洋工程有限公司，江苏启东 226251；4.中远海运重工有限公司，上海 200135；5.江苏中天科技股份有限公司，江苏南通 226000）

0 引言

我国海岸线长1.8万km，风能资源丰富，据估计近海可开发的风能约7.5亿kW，是陆地的2.96倍。“十四五”规划中，我国将海上风电作为解决能源危机、降低环境污染、实现“双碳目标”的国家战略[1-5]。近年来，随着我国海上风电的迅猛发展，海上风电装机容量也逐年增加，风机叶片的尺寸也逐渐从长几十米向上百米过渡，2021年8月，10 MW海上风电机组“海电运维801”在福建长乐外海顺利完成了吊装，标志着外海深水区大机型海上风电安装实现从无到有的历史性跨越[6-7]。此次吊装的风机为东方电气10 MW风电机组，发电机重量达270 t（不含吊具和支架重量），轮毂中心高度达到118 m，单只叶片长度90 m。随着风机的大型化，实施大型风机安装对接过程的空中高度也逐渐增大，单叶片在吊装和高空对接过程中所受的风载荷也随之增大，为单叶片在高空中的平稳对接安装带来了不小的难题[8-9]。由于叶片长度和尺寸的增加，叶片的刚度进一步降低，如在高空对接过程中发生对接螺孔的冲击碰撞[10]，极易造成叶片的根部损坏，从而造成巨大的经济损失。因此，如何在风载荷较大的高空环境下实现大型海上风机叶片的平稳对中安装是亟待解决和研究的问题之一。

目前，国内外研究人员在大型风机叶片的吊装和安装过程的稳定性等方面做出了研究。Fang等[11]借鉴了起重机吊装作业过程中减小货物空中摆动的自动控制方法，研究了通过相应自动控制方法提高吊装精度和吊装效率的可能性。Ren等[12]通过扩展卡尔曼滤波（Extended Kalman Filter，EKF）与比例积分微分（Proportional-integral-derivative，PID）控制相结合的方法，研究了对叶片空中姿态进行调整的自动控制方法，降低了叶片的对中难度。在此基础上，上海海事大学的郭佳民等[13]引入了精度较高的无迹卡尔曼滤波（Unscented Kalman Filter，UKF）与PID相结合的主动闭环控制系统，并模拟了单叶片按照三种预期吊装路线吊装到高空110 m过程中的吊装控制，结果表明，UKF可以显著降低缆风绳主动控制力的变化率，从而降低整个控制系统中硬件设备的响应要求，经济性更好。Verma等[14]建立了带有T型螺栓连接的叶根的三维有限元模型，并对导向连接冲击轮毂的情况进行了冲击研究，讨论了在叶片高空对接过程中叶根处发生冲击碰撞时的失效形式及对应结果。

本文旨在建立大型海上风机单叶片高空对接过程的力学分析模型，以NERL 5MW[15]标准海上风机叶片为研究对象，首先分析叶片在高空安装作业时不同空中姿态下风载荷对其升力、阻力及俯仰矩的影响规律；然后建立以叶片为研究对象的准静态力学平衡方程组，对其6个自由度进行准静态平衡分析，研究高空中风速变化对吊索和缆风绳中的控制力大小和方向所造成的影响，通过解有约束的线性方程组，给出叶片在保持某一空中姿态下使系统保持准静态平衡时缆风绳中所需的最小拉力，研究了吊索作用位置及风速变化对缆风绳中拉力的影响规律。该研究将为大型海上风机单叶片的高空对接过程提供理论指导，并为缆风绳及吊索对应的自动控制系统的设计及优化提供设计参考。

1 大型海上风机单叶片的高空对接过程

大型海上风机的单叶片的安装过程包括吊装和高空对接两个阶段，如图1所示，叶片被夹具夹紧并由起重机的吊索吊起并逐渐升空，到达高空对接位置处时再开始对接过程，在夹具的另一端则有绞机控制的两条缆风绳通过对其控制力的实时调整来减少高空中风载荷的作用对叶片姿态的扰动，使叶片保持预定的吊装路线和空中姿态，最终实现叶片的吊装和平稳对中。在吊装过程中，叶片及夹具、起重机、绞车和连接它们的吊索和缆风绳共同构成一个多体动力学系统，而在高空对接过程中，叶片及夹具可视为一个整体，在吊索和缆风绳及风载荷的共同作用下在高空中保持准静态平衡，在定位销的作用下实现螺栓与螺孔的对接，如图2所示。在本文中，主要讨论高空中叶片的安装对接过程，因此可将其单叶片视为具有6个自由度（6个方向的平动自由度和6个方向的转动自由度）的刚体进行建模分析。

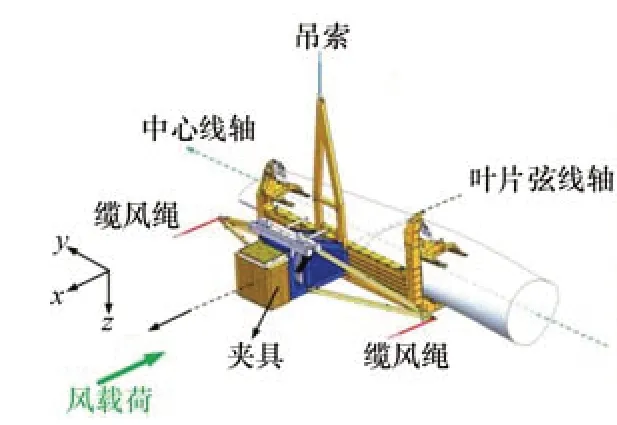
图1 单叶片吊装及对接过程中的各部分位置分布

图2 叶片的高空对接过程

1.1 叶片的截面数据

叶片的截面如图3所示，以叶根处的截面重心为坐标原点，建立叶片坐标系{B}，其中，沿迎风方向为x轴，沿翼展方向为y轴，竖直向下方向为z轴。为了计算叶片所受空气动力载荷，沿翼展方向将叶片分为i个截面，其中每个截面i的主要参数有重心坐标pCOG,i，空气动力中心坐标pC1/2,i，压力中心坐标pC1/4,i，叶片厚度ti，叶片弦长Ci，叶片水平时弦线与风向的夹角α，空气动力扭角θy,i，攻角αi（the angle of attack，AOA）的计算公式为：

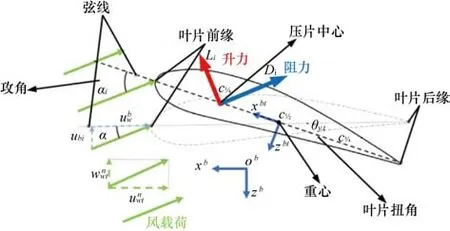
图3 叶片第i个截面内参数示意图

其中α通过下式给出：

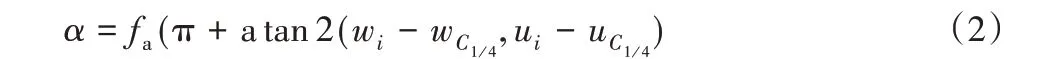
式中：wi和ui为风载荷在x-z面内的两个方向的矢量；atan2为多值反正切函数；wi-wC14和ui-uC14分别为风速在第i个截面内的相对速度；fa为将角度转化到[-π,π)范围内的量。

本文中标准NERL 5MW风机没有预弯曲，因此其中心线几乎为直线，连接了从叶根到叶尖处的所有空气动力中心pC1/2,i，截面数据通过丹麦DTU公司开发的HAWC2软件内置的叶片尺寸标准数据库得到，其中i=0,…,48，叶片总长lb=61 m，叶片质量mb=17.74 t，夹具质量my=20 t。

1.2 叶片的空中姿态及旋转矩阵

叶片在空中的姿态及风载荷相对于叶片的方向由3个欧拉旋转角φ，θ和ψ决定，风载荷矢量在x-y平面内绕z轴的转动由偏航角（yaw）ψ定义，而绕y轴的俯仰角（pitch）由θ定义，绕x轴转动的翻滚角（roll）由φ所定义，为避免万向锁效应（第2次转动为±90°时，转动矩阵奇异）产生，不采用常规的roll-pitch-yaw顺规，而采用pitch-roll-yaw顺规，因为在单叶片的安装过程中，pitch和yaw均可能达到±90°，但roll并不能达到±90°（此时叶片的根部和尾部将在空中竖起），所以采用此顺规是合理的。

设全局坐标系为{N}，叶片初始水平状态下，{B}与{N}保持重合，而叶片在空中姿态发生转动后，相当于{B}左乘了欧拉角对应的旋转矩阵Rnb，其中上标b、下标n代表从坐标系{B}转化到坐标系{N}，对应的Rnb可表示为下式：

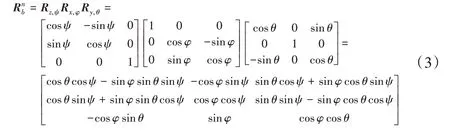
值得注意的是，欧拉角所构成的旋转矩阵是正定阵，即(Rnb)T=(Rnb)-1，所以从坐标系{N}转化到坐标系{B}可以表示为Rbn=(Rnb)-1=(Rnb)T，即左乘Rnb的转置。

对于位于整体坐标系{N}中风载荷，计算迎风面积时需要将风载荷转化到叶片坐标系{B}中，即：

式中：α为叶片攻角减去空气动力扭角θy,i后得到的值，即与风向的夹角。

单叶片的空中姿态所对应的欧拉角如图4所示。

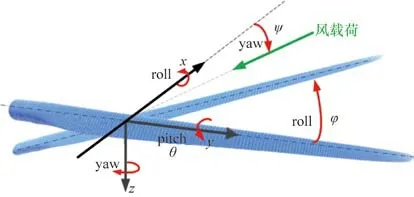
图4 单叶片的空中姿态所对应的欧拉角

1.3 单叶片安装过程中的空气动力学模型

在准静态分析中，叶片的空气动力学系数是攻角αi和翼型的相对厚度（T/C）的函数，定义T/Ci=ti/Ci，其中ti和Ci分别为第i个截面内的叶片最大厚度与叶片弦长，则第i个截面的升力系数Cl，阻力系数Cd和俯仰矩系数CM及第i个截面的升力系数Li，阻力系数Di和俯仰矩系数Mi可通过标准NERL 5MW风机的数据库数据中插值得到[16]：

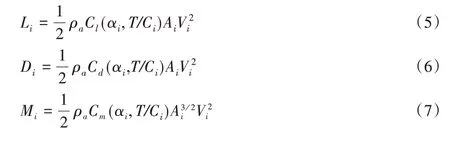
其中下标i代表第i个节点，ρa=1.29 kg/m3为空气密度，Vi为流入速度，根据横流效应，沿翼型方向的风载荷可忽略不计；Ai为叶片受风面积，可由下式计算得出：

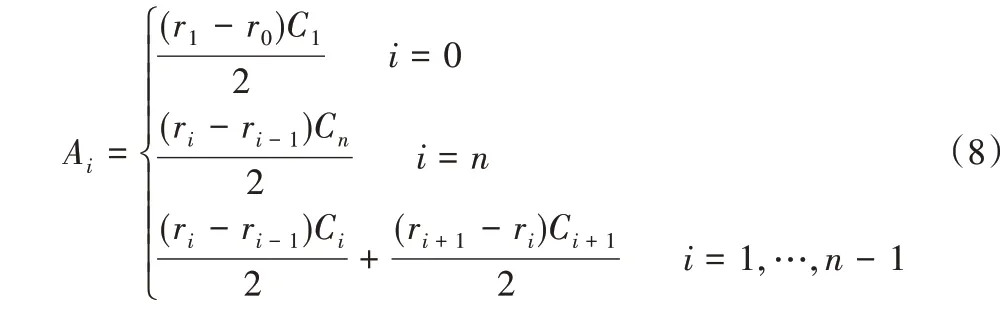
因此，风载荷作用在第i个截面的叶片力载荷Fw,i和力载荷所造成的力矩Mw,i可分别表示为：

而风载荷作用在叶片上的总载荷τw可以表示为：

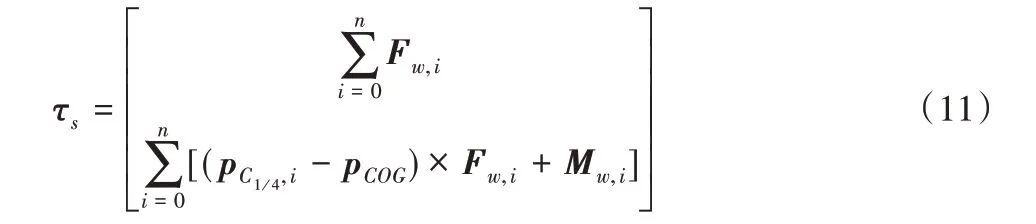
式中：(pC14,i-pCOG)为第i截面到叶片重心的力臂。

1.4 单叶片保持空中姿态时的准静态平衡方程

为了简化分析，将叶片视为具有6个自由度（3个方向的平动自由度和3个方向的转动自由度）的刚体，将夹具与叶片视为相互刚性固定的整体，夹具的重心与叶片的重心重合在一点，并忽略夹具的惯性矩，夹具上的吊索固定在叶片重心周围，主要提供提升的拉力，而缆风绳则主要起辅助作用，控制叶片的空中姿态和吊装轨迹。叶片保持空中姿态准备对接安装时，没有平动加速度和转动角速度，其对应的准静态平衡方程为：

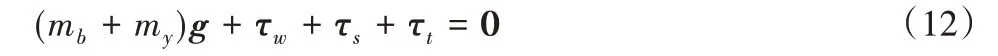
式中：g=[0,0,g,0,0,0]T，g为重力加速度；τw、τs和τt分别为风总载荷、吊索总载荷和缆风绳总载荷。

设吊索施加的载荷矢量为Fs，作用位置在{B}下的矢量为ps，则吊索所提供的总载荷可表示为：

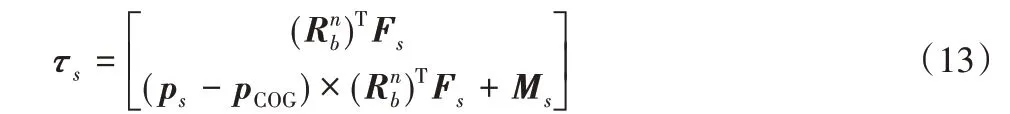
设两条缆风绳施加的载荷矢量为Fti，作用位置在{B}坐标系下的矢量为pti，则缆风绳所提供的总载荷可表示为：

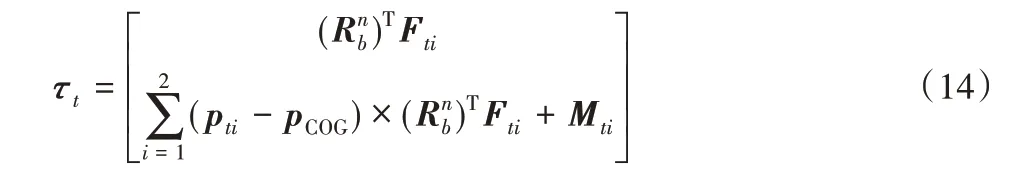
设吊索的载荷矢量在{B}坐标系下为Fs=[Fsx,Fsy,Fsz]T，作用力臂的空间矢量ls=(ps-pCOG)=[lsx,lsy,lsz]T，两条缆风绳的载荷矢量在{B}坐标系下为分别为Ft1=[Ftx1,Fty1,Ftz1]T和Ft2=[Ftx2,Fty2,Ftz2]T，作用力臂的两个空间矢量lt1=(pt1-pCOG)=[ltx1,lty1,ltz1]T和lt2=(pt2-pCOG)=[ltx2,lty2,ltz2]T，则可将式（12）整理成下列矩阵：

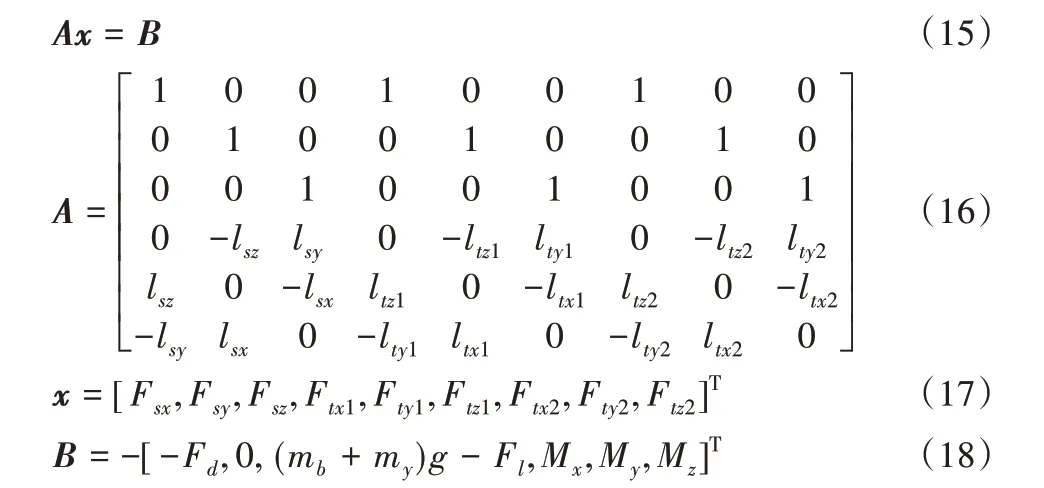
从上式中可以看出，一共有6个线性方程，但是有9个未知数，是典型的不定方程问题，此时需要引入约束条件，即绳子的拉力{Ts,Tt1,Tt2}≥0，通过引入约束方程，采用MATLAB中的非线性约束函数Fmincon，可以求出使叶片在空中某一姿态保持平衡时缆风绳所需的最小拉力。

2 单叶片所受空气动力载荷变化规律

2.1 单叶片空气动力学系数随相对厚度和攻角的变化规律

本文所研究的标准NERL 5MW海上风机的空气动力学系数在不同翼型相对厚度下随攻角变化的曲线分别如图5～7所示，从图中可以看出，对于该类型风机叶片，升力系数在不同翼型相对厚度下均在攻角10°左右时取得极大值，当T/C=40%时，升力系数最大；阻力系数在T/C=40%时最大；而俯仰矩在攻角±120°左右时分别取得极小值和极大值，翼型相对厚度对俯仰矩系数的影响不大。

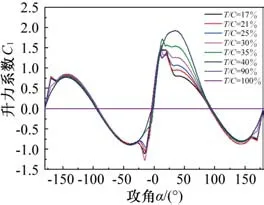
图5 NERL 5MW标准风机的升力系数Cl随翼型相对厚度和攻角的变化规律

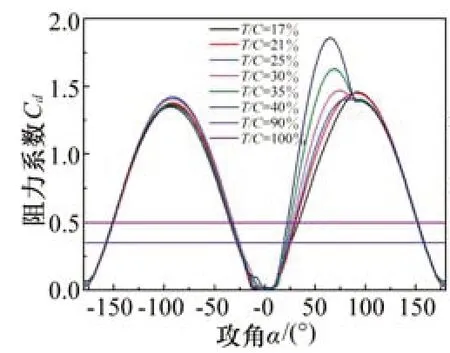
图6 NERL 5MW标准风机阻力系数随翼型相对厚度和攻角变化规律

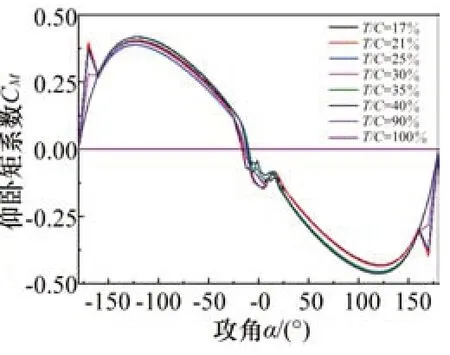
图7 NERL 5MW标准风机俯仰矩系数随翼型相对厚度和攻角变化规律

2.2 单叶片空气动力学系数随俯仰角的变化规律

标准NERL 5MW海上风机在不同俯仰角θ下叶片上的空气动力学系数分别如图8～10所示。从图8中可以看出，当俯仰角在10°～30°时，叶片上距离叶根超过10 m的位置均具有较大的升力系数，当俯仰角在40°左右时，升力系数在距离叶根10 m左右的叶片区域内取得最大值；在俯仰角超过40°之后，随着俯仰角的逐渐增大，升力系数逐渐减小。从图9中可以看出，当俯仰角在80°左右时，阻力系数在距离叶根10 m左右的叶片区域内取得最大值；当俯仰角低于30°时，阻力系数较小且变化不大。从图10中可以看出，距离叶根10 m以内的区域俯仰矩较小；随着俯仰矩的增大，叶片整体的俯仰矩绝对值也逐渐增大，负值代表有使水平放置的叶片抬头的趋势。

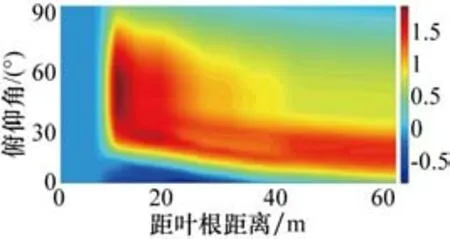
图8 NERL 5MW标准风机的升力系数Cl随俯仰角的变化规律

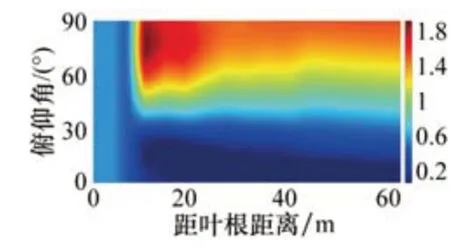
图9 NERL 5MW标准风机阻力系数随俯仰角变化规律

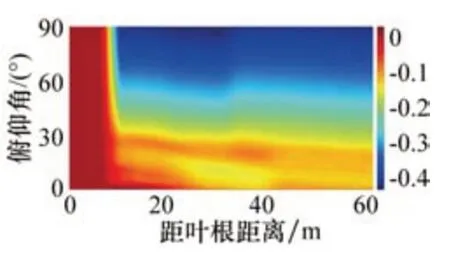
图10 NERL 5MW标准风机俯仰矩系数随俯仰角变化规律

2.3 单叶片所受风载荷随俯仰角的变化规律

标准NERL 5MW海上风机在不同俯仰角θ下叶片上所受单位长度升力和阻力分别如图11、图12所示。从图11可以看出，单位长度升力的分布规律与升力系数的分布规律大致相同，但在低俯仰角时，叶片上的单位升力在距离叶根10 m左右最大，叶尖处的升力系数虽然大，但单位升力较小。从图12可以看出，单位长度阻力的分布规律与阻力系数的分布规律大致相同，在高俯仰角时，在距离叶根10 m左右处单位长度阻力最大，叶尖处的阻力系数虽然比较大，但单位长度阻力较小。

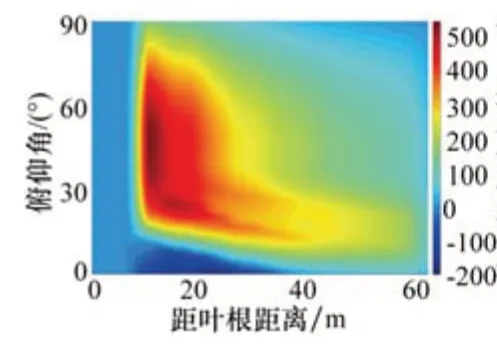
图11 NERL 5MW标准风机单叶片单位长度升力随俯仰角变化规律

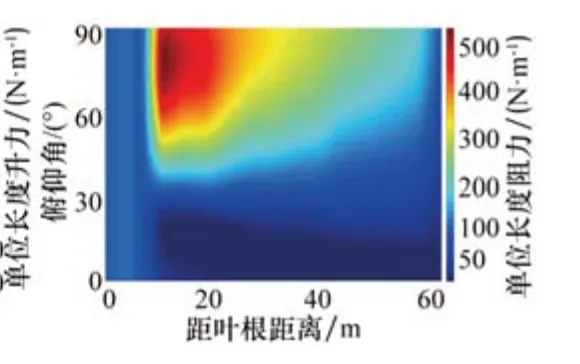
图12 NERL 5MW标准风机单叶片单位长度阻力随俯仰角变化规律

2.4 单叶片所受总风载荷随风速的变化规律

标准NERL 5MW海上风机在不同俯仰角θ下叶片上所受总升力和总阻力随风速的变化规律分别如图13、图14所示。从图13可以看出，总升力与风速的平方成比例，这点可以由式（5）看出，而俯仰角20°左右时叶片所受到的总升力最大，在俯仰角小于10°时，升力为负值，说明此时叶片将受到向下的合力。从图14可以看出，总阻力也与风速的平方成比例，这点可以由式（6）看出，而在低俯仰角时叶片所受到的总阻力有限，且风速的增加并没有显著增加总阻力，这是因为此时的阻力系数也很小；而在大俯仰角时（俯仰角大于70°），叶片所受到的总阻力会急剧增加，负值代表阻力从叶片前缘指向叶尖。

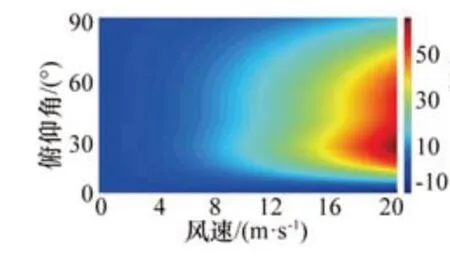
图13 NERL 5MW标准风机单叶片总升力随风速的变化规律

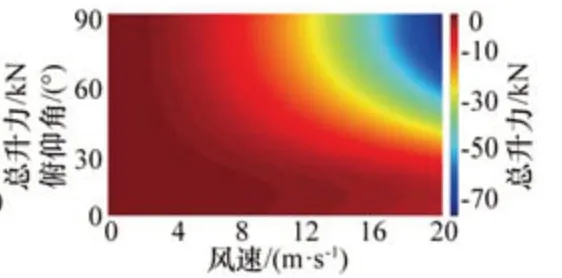
图14 NERL 5MW标准风机单叶片总阻力随风速的变化规律

3 单叶片高空对接过程中的准静态平衡及绳子拉力

在大型海上风机单叶片的高空对接过程中，假设其在某一姿态保持准静态平衡，则此时吊索和缆风绳除了需要提供叶片和夹具的重力之外，还需要提供与风载荷造成的升力、阻力和俯仰矩相互抵消的力矩。将叶片与夹具看成一个刚性整体，其重心也位于叶片重心，假设缆风绳与地面的夹角γ=0，即缆风绳被水平固定，Ft1=[Ftx1,Fty1,0]T和Ft1=[Ftx1,Fty1,0]T，吊索的作用力臂空间矢量为ls=(ps-pCOG)=[0,0,0]T，两条缆风绳的作用力臂空间矢量分别为lt1=(pt1-pCOG)=[-2,-4.5,2]T和lt2=(pt2-pCOG)=[-2,4.5,2]T，即吊索的对刚性整体只有力而没有力矩作用，两条缆风绳分别左右对称固定在叶片的下部。在叶片的空中姿态保持初始水平时，即欧拉旋转矩阵=R([0,0,0]T)时，得到的缆风绳最小拉力随风速变化的曲线如图15所示。从图中可以看出，随着风速的增加，两条缆风绳中的最小拉力均逐渐增大，但增加的幅度不一样，这是因为需要两条缆风绳提供不同的拉力来平衡风载荷所造成的俯仰矩。

图15 NERL 5MW标准风机单叶片保持空中姿态不变时不同风速下缆风绳最小拉力(吊索作用力臂(0，0，0))

如果吊索的作用力臂空间矢量为ls=(ps-pCOG)=[-0.5,0,0]T，即吊索的作用点并没有位于叶片的重心，从而对刚性整体有力矩作用时，其他条件相同的情况下，得到的缆风绳最小拉力随风速变化的曲线如图16所示。从图中可以看出，随着风速的增加，两条缆风绳中的最小拉力均逐渐增大，但增加的幅度不一样；与图15相比，相同风速下两条缆风绳中的拉力显著增大，这是因为竖直方向上平衡叶片与夹具重力的吊索拉力由于其作用位置没有经过叶片重心，导致对叶片有较大的力矩作用，而为了平衡其力矩作用，在两条缆风绳中需要提供较大的水平力来平衡吊索额外造成的力矩。在实际吊装和高空对接过程中，吊索所能承受的绳子拉力是要远大于缆风绳的，而缆风绳中过大的拉力易造成其断裂，从而引发安全事故。因此，要保证单叶片在高空中的安全对接，要合理地控制吊索的吊装位置，避免其偏离叶片重心过远，使缆风绳承受过大的平衡拉力。

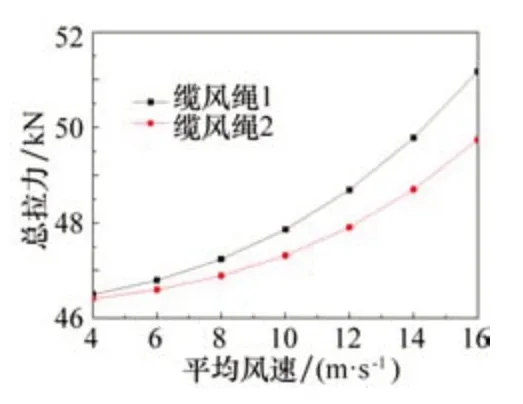
图16 NERL 5MW标准风机单叶片保持空中姿态不变时不同风速下缆风绳最小拉力(吊索作用力臂(-2，0，0))

4 结束语

本文研究了大型海上风机单叶片高空对接过程中保持准静态平衡时的力学模型，以标准NERL 5MW海上风机单叶片为研究对象，基于丹麦DTU公司开发的HAWC2软件内置的叶片尺寸标准数据库，对叶片在高空安装作业时不同空中姿态下风载荷对其升力、阻力及俯仰矩进行了计算，然后建立了以叶片为研究对象的准静态力学平衡方程组，对其6个自由度进行准静态平衡分析，研究高空中风速变化对吊索和缆风绳中的控制力大小和方向所造成的影响，通过解有约束的线性方程组，给出叶片在不同空中姿态下使系统保持动态平衡时缆风绳中所需的最小拉力，其结论如下。

（1）对于标准NERL 5MW海上风机叶片，叶片的升力系数在不同翼型相对厚度下均在攻角10°左右时取得极大值，当T/C=40%时，升力系数最大；阻力系数在T/C=40%时最大；而俯仰矩在攻角±120°左右时分别取得极小值和极大值，翼型相对厚度对俯仰矩系数的影响不大。

（2）对于叶片的空气动力学系数随俯仰角的变化规律，当俯仰角在40°左右时，升力系数在距离叶根10 m左右的叶片区域内取得最大值；在俯仰角超过40°之后，随着俯仰角的逐渐增大，升力系数的逐渐减小。当俯仰角在80°左右时，阻力系数在距离叶根10 m左右的叶片区域内取得最大值；当俯仰角低于30°时，阻力系数较小且变化不大。距离叶根10 m以内的区域俯仰矩较小；随着俯仰矩的增大，叶片整体的俯仰矩绝对值也逐渐增大。

（3）单位长度升力的分布规律与升力系数的分布规律大致相同，但在低俯仰角时，叶片上的单位升力在距离叶根10 m左右最大，叶尖处的升力系数虽然大，但单位升力较小。从图12可以看出，单位长度阻力的分布规律与阻力系数的分布规律大致相同，在高俯仰角时，在距离叶根10 m左右处单位长度阻力最大，叶尖处的阻力系数虽然比较大，但单位长度阻力较小。

（4）叶片所受总升力与总阻力均与风速的平方成比例，俯仰角在20°左右时叶片所受到的总升力最大，在俯仰角小于10°时，升力为负值，说明此时叶片将受到向下的合力。在低俯仰角时叶片所受到的总阻力有限，且风速的增加并没有显著增加总阻力，这是因为此时的阻力系数也很小；而在大俯仰角时（俯仰角大于70°），叶片所受到的总阻力会急剧增加，负值代表阻力从叶片前缘指向叶尖。

（5）当吊索的作用位置经过叶片重心时，随着风速的增大，两条缆风绳中的最小拉力均逐渐增大，但增加的幅度不一样，这是因为需要两条缆风绳提供不同的拉力来平衡风载荷所造成的俯仰矩；而当吊索的作用位置偏离叶片重心时，其对叶片有较大的力矩作用，为了平衡其力矩作用，相同风速下两条缆风绳中的拉力显著增大。因此要保证单叶片在高空中的安全对接，要合理地控制吊索的吊装位置，避免其偏离叶片重心过远，使缆风绳承受过大的平衡拉力。