ImCn的循环区间全着色

张泽堃，亢 明，赵永强

（1.河北地质大学 数理学院，河北 石家庄 050031；2.中国地质大学（北京）数理学院，北京 100083）

0 引言

首先介绍一些概念与符号.用V（G）和E（G）表示图G的顶点集和边集.对于顶点vV（G），用dG（v）表示v的度，用Δ（G）表示G的最大度.

用|A|表示有限集A的元素个数.任意非空的由连续整数构成的集合称为区间.最小和最大元素分别为x和y的区间记作[x，y].由区间[x，y]中所有偶数构成的集合与所有奇数构成的集合分别记作e[x，y]和o[x，y].如果|M|=k，则称区间|M|为k-区间.

图的全着色概念分别由Vizing[1]与Behzad[2]独立提出.

定义1[1，2]图G的t-全着色为映射α：E（G）∪V（G）→[1，t]，使得任意相邻的顶点、相邻的边以及相互关联的顶点和边均着色不同.

对于图G的全着色α以及任意顶点vV（G），令S[α，v]={α[v]}∪{α[e]|e与v关联}.最近文献[3-5]推广了图的区间着色[6，7]以及区间全着色[8，9]概念，定义并研究了图的循环区间全着色.

定义2[3]如果图G的t-全着色α满足下列条件：对任意xV（G），集合S[α，v]为[dG（v）+1]-区间，或者{1，t}S[α，v]为[t-dG（v）-1]-区间.则称α为G的循环区间t-全着色.

如果存在某个整数t，使得图G有一个循环区间t-全着色，则称G为可循环区间全着色的.所有可循环区间全着色的图构成的集合记作F.

对于任意图GF，其循环区间全着色所需最少与最多颜色数分别记作和.

2016年，王楠楠[3]研究了路Pn、圈Cn、轮图Wn、完全图Kn、完全二部图Km，n以及完全三部图K1，m，n的循环区间全着色.2017年，Zhao等[4]研究了圈Cn以及圈的中间图M（Cn）的循环区间全着色.2018年，Su等[5]研究了圈的单点结合图的循环区间全着色.

定义3[10]图G和H的并记作G∪H，其顶点集为V（G）∪V（H），边集为E（G）∪E（H）.如果G和H不相交，则称其并为不交并，记作G+H.从图G和H的不交并开始，将G中的每个顶点与H的任一顶点连接，得到的图称为G和H的联图，记作GH.

注意到轮图其实就是一个孤立顶点与圈的联图，孤立顶点就是仅有一个顶点的空图.所以空图Im与圈Cn的联图ImCn（m≥1，n≥3）可视为轮图Wn的推广.笔者研究ImCn的循环区间全着色，文中用到但未详细说明的图论概念见文献[10，11].为了方便，令V（Im）={u1，u1，…，um}，V（Cn）={v1，v1，…，vn}，其中m≥1，n≥3.

2016年，王楠楠研究了轮图Wn的循环区间全着色，并得到如下结果.

定理1[3]当整数n≥4时，有WnF，并且

由于Wn=I1Cn-1，所以由定理1立即可得下面的结果.

推论1当整数n≥3时，有I1CnF，并且.

引理1对于任意整数m≥2，如果n=m+1，则有ImCnF，并且=n+2.

证明：假设整数m≥2并且n=m+1.下面分两种情况讨论.

情形1：m为奇数.

构造ImCn的一个（n+2）-全着色α.令

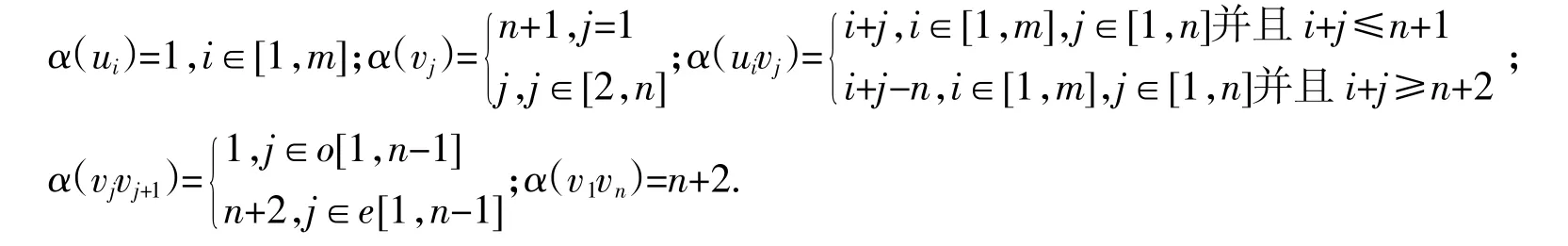
I3C4的6-全着色如图1所示.

图1 I3C4的6-全着色

根据α的定义可知：S[α，ui]=[1，m+2]，i[1，m]；S[α，vj]=[1，m+3]，j[1，m+1].这就证明α是ImCn的一个循环区间（n+2）-全着色，并且有≤n+2.

情形2：m为偶数.

构造ImCn的一个（n+2）-全着色α.令

重新把umv2着色为α（umv2）=n+2.I4C5的7-全着色如图2所示.

图2 I4C5的7-全着色

根据α的定义可知S[α，ui]=[2，n+2]，i[1，m]；S[α，vj]=[1，n+2]，j[1，n].这就证明α是ImCn的一个循环区间（n+2）-全着色，并且有≤n+2.

综合情形1和2可知，当m≥2并且n=m+1时，有ImCnF，并且≤n+2.另一方面，由于此时⊿（ImCn）=n+1，所以有+1=n+2.因此=n+2.

引理2对于任意整数m≥2，如果n=m+2，则有ImCnF，并且当m为偶数时，有=n+1；当m为奇数时，有≤n+2.

证明：假设整数m≥2并且n=m+2.下面分两种情况来讨论.

情形1：m为偶数.

I2C4的一个循环区间5-全着色如图3所示.

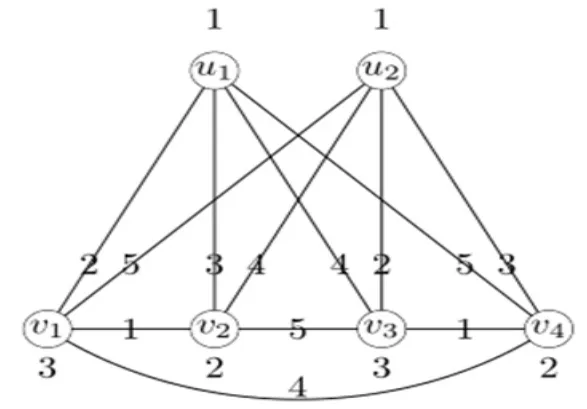
图3 I2C4的5-全着色

下面构造ImCn（m≥4）的一个（n+1）-全着色α.令

I4C6的7-全着色如图4所示.

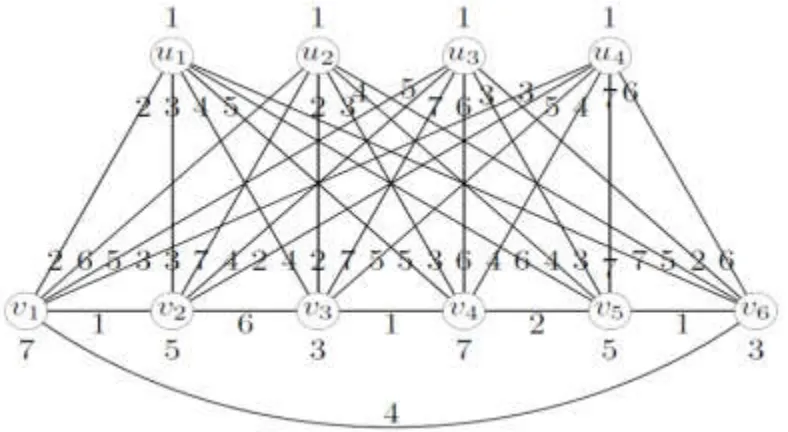
图4 I4C6的7-全着色

根据α的定义可知S[α，ui]=S[α，vj]=[1，n+1]，i[1，m]，j[1，n].这就证明α是ImCn的一个循环区间（n+1）-全着色，并且有

情形2：m为奇数.

构造ImCn的一个（n+2）-全着色α.令

I3C5的7-全着色如图5所示.

图5 I3C5的7-全着色

根据α的定义可知S[α，ui]=[1，n+1]，i[1，m]；S[α，vj]=这就证明α是ImCn的一个循环区间（n+2）-全着色，并且有

由于此时⊿（ImCn）=n，所以有+1=n+1.综合情形1和2可知，结论成立.

引理3对于任意整数m≥2，如果n≥m+3，则有ImCnF，并且=n+1.

证明：假设整数m≥2并且n≥m+3.下面分两种情况讨论.

情形1：m为奇数.

构造ImCn的一个（n+1）-全着色α.令

I3C7的8-全着色如图6所示.

图6 I3C7的8-全着色

根据α的定义可知S[α，ui]=[1，n+1]，i[1，m]；

是ImCn的一个循环区间（n+1）-全着色，并且有

情形2：m为偶数.

构造ImCn的一个（n+1）-全着色α.令

I4C7的8-全着色如图7所示.

图7 I4C7的8-全着色

根据的定义可知S[α，ui]=[1，n+1]，i[1，m]；

ImCn的一个循环区间（n+1）-全着色，并且有

综合情形1和2可知，当m≥2并且n≥m+3时，有ImCnF，并且≤n+1.另一方面，由于此时⊿（ImCn）=n，所以有.因此

综合引理1～3可得下面结果.

定理2对于任意整数n＞m≥2，有ImCnF，并且：1）当n=m+1时，=n+2；2）当n=m+2且m为奇数时，n+1≤n+2；3）当n≥m+3，或当n=m+2且m为偶数时，=n+1.

定理3对于任意整数m≥n≥3，有

证明：假设整数m，n满足m≥n≥3.首先给出ImCn的顶点和边的一个（m+3）-着色α.令

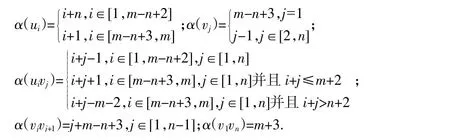
注意：根据α的定义，一方面，当i[1，m-n+1]或i[m-n+3，m-1]时，有α（ui+1）=α（ui）+1且α（u1）=n+1，α（um-n+3）=m-n+4；另一方面，α（v1）=m-n+3且当j[2，n-1]时，有α（vj+1）=α（vj）+1且α（vn）=n-1.下面分情况进行讨论.

情形1：m=2n-3.

一方面，min{α（ui）|i[1，m-n+2]}=α（u1）=n+1，min{α（ui）|i[m-n+3，m]}=α（um-n+3）=n+1.

另一方面，α（v1）=m-n+3=n，max{α（vj）|j[2，n]}=α（vn）=n-1.

从而对于任意i[1，m]和j[1，n]，有α（ui）＞α（vj）.所以不难检验α为ImCn的一个（m+3）-全着色.I3C3的6-全着色如图8所示.

图8 I3C3的6-全着色

根据α的定义可知

所以α是ImCn的一个循环区间（m+3）-全着色.

情形2：m=2n-4.

因为3≤n≤m=2n-4，所以m≥n≥4.

一方面，min{α（ui）|i[1，m-n+2]}=α（u1）=n+1，min{α（ui）|i[m-n+3，m]}=α（um-n+3）=n.

另一方面，α（v1）=m-n+3=n-1，max{α（vj）|j[2，n]}=α（vn）=n-1.

可以注意到，虽然对于任意i[1，m]和j[1，n]，α（ui）＞α（vj）仍成立，但此时有α（v1）=α（vn）=n-1.为此把vn和um-n+3vn分别重新着色为α（vn）=1和α（um-n+3vn）=n-1.不难检验，此时α为ImCn的一个（m+3）-全着色.I4C4的7-全着色如图9所示.

图9 I4C4的7-全着色

根据α的定义有

所以α是ImCn的一个循环区间（m+3）-全着色.

情形3：m≤2n-5.

因为3≤n≤m≤2n-5，所以m≥n≥5且有α（um-n+3）=m-n+4≤n-1=α（vn）.从而有：

对于任意j[m-n+5，n]，把vj和un-1vj分别重新着色为α（vj）=j-m+n-3和α（un-1vj）=j-1.此时S[α，un-1]=[m-n+4，m+3]∪{1}且对于任意wV（ImCn){un-1}，S[α，w]保持不变.

注意此时α（vn）=2n-m-3.如果仍有α（um-n+3）=m-n+4≤2n-m-3=α（vn），即：

则对于任意j[2m-2n+7，n]，把vj和u2n-m-3vj分别重新着色为α（vj）=j-2m+2n-5和α（un-1vj）=j-m+n-3.此时S[α，u2n-m-3]=[m-n+4，m+3]∪{1}且对于任意wV（ImCn){u2n-m-3}，S[α，w]保持不变.

注意此时α（vn）=3n-2m-5.如果仍有α（um-n+3）≤α（vn），则重复上面过程，直至α（um-n+3）＞α（vn）为止.

如果上述过程结束后有α（v1）=α（vn），则重复情形2的操作.不难检验，此时α为ImCn的一个循环区间（m+3）-全着色.I5C5的8-全着色如图10所示.

图10 I5C5的8-全着色

情形4：m≥2n-2.

因为m≥2n-2，所以α（um-n+3）=m-n+4≥n+2.又因为α（u1）=n+1，α（vn）=n-1，所以对于任意i[1，m]与j[2，n]，总有α（ui）＞α（vj）.一方面，因为m≥2n-2，所以α（v1）=m-n+3≥n+1=α（u1）.另一方面，因为n≥3，所以α（v1）=m-n+3≤m=α（um-n）.由于α（uk）在[1，m-n]上是递增的，所以存在k[1，m-n]，使得α（v1）=α（uk）.

子情形4.1：k=1.

即α（v1）=α（u1）.把u1重新着色为α（u1）=m+3.此时不难验证α为ImCn的一个（m+3）-全着色.根据α的定义有S[α，u1]=[1，n]∪{m+3}且对于任意wV（ImCn){u1}，S[α，w]保持不变.所以为α为ImCn一个循环区间（m+3）-全着色.I4C3的7-全着色如图11所示.

图11 I4C3的7-全着色

子情形4.2：k=2.

即m-n+3=α（v1）=α（u2）=n+2，也即m=2n-1.当n=3时，m=5.把I5C3重新着色如下.令

再重新把u3v3，u4v3以u5v3及分别着色为α（u3v3）=2，α（u4v3）=5，α（u5v3）=1.不难检验α为I5C3的一个8-全着色.根据α的定义可知S[α，u1]=[1，3]∪{8}，S[α，u2]=S[α，u3]=[2，5]，S[α，u4]=[5，8]，S[α，u5]=[6，8]∪{1}，S[α，vj]=[1，8]，j[1，3].

所以α为I5C3的一个循环区间8-全着色.I5C3的循环区间8-全着色如图12所示.

图12 I5C3的8-全着色

当n≥4时，m≥7.把v1，u2以及v1u2重新着色为α（v1）=2，α（u2）=m-n+4=n+3，α（v1u2）=m-n+3=n+2.不难检验α为ImCn的一个（m+3）-全着色.此时S[α，u2]=[3，n+3]且对于任意wV（ImCn){u2}，S[α，w]保持不变.所以α为ImCn的一个循环区间（m+3）-全着色.I7C4的10-全着色如图13所示.

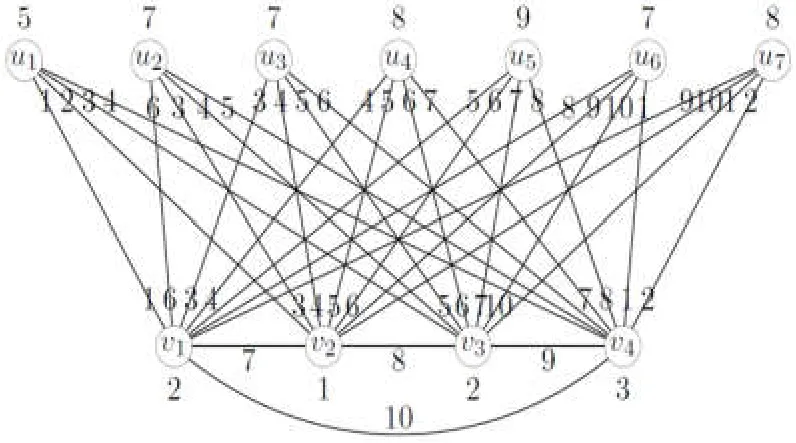
图13 I7C4的10-全着色

子情形4.3：k[3，m-n].

即m-n+3=α（v1）=α（uk）=k+n，这里k[3，m-n].

如果k=n-1=α（vn）.则把v1和v1uk-1分别重新着色为α（v1）=k-1和α（v1uk-1）=m-n+3=k+n.此时不难检验为α为ImCn的一个循环区间（m+3）-全着色.根据α的定义可知S[α，uk-1]=[k，k+n]且对于任意wV（ImCn){uk-1}，S[α，w]保持不变.所以α为ImCn的一个循环区间（m+3）-全着色.I8C4的循环区间11-全着色如图14所示.

图14 I8C4的11-全着色

如果k≠n-1=α（vn）.则把v1，uk以及v1uk分别重新着色为α（v1）=k，α（uk）=m-n+4=k+n+1和α（v1uk）=m-n+3=k+n.此时不难检验α为ImCn的一个（m+3）-全着色.根据α的定义可知S[α，uk]=[k+1，k+n+1]且对于任意wV（ImCn){uk}，S[α，w]保持不变.所以α为ImCn的一个循环区间（m+3）-全着色.I6C3的9-全着色如图15所示.

图15 I6C3的9-全着色

综合子情形4.1～4.3，当m≥2n-2时，ImCn存在一个循环区间（m+3）-全着色.

综合情形1～4，当m≥n≥3时，ImCnF且w（ImCn)≤m+3.另一方面，由于⊿（ImCn）=m+2，所以有.因此

3 总结

研究了空图Im与圈Cn的联图ImCn的循环区间全着色，证明对于任意整数m≥2，n≥3，ImCn均为可循环区间全着色的，并且得到如下结果：

1）当n=m+1时；

2）当n=m+2且m为奇数时，n+1≤

3）当n≥m+3，或当n=m+2且m为偶数时，

4）当m≥n时，

虽然如此，当n=m+2且m≥2为奇数时，的准确值还没能确定.另外，关于的取值也有待研究.